基于现场监测位移的隧道围岩参数反演分析
2022-07-08毕钛俊
赵 亮, 毕钛俊
(1.云南交投集团公路建设有限公司, 昆明 650100; 2.中国科学院 武汉岩土力学研究所, 岩土力学与工程国家重点实验室, 武汉 430071; 3.中国科学院大学, 北京 100049)
隧道工程在中国已经得到广泛发展,控制隧道围岩变化,增加围岩的稳定性和承载能力极为重要。由于岩土工程介质的复杂性和不可预测性,确定岩土工程材料的物理参数是一个难题。数值方法的发展极大地提高了各种岩土工程的应力、位移和破坏分析的效率。基于现场测量数据对岩土工程材料参数的反分析通常比实验室试验结果更可靠。
位移反分析是目前岩土工程反分析中使用最广泛的方法。陈敬松等[1]利用有限元反演理论,建立二维弹塑有限元计算模型,进行数值模拟,分析浅埋连拱隧道施工时围岩和中墙的受力变形规律。徐建国等[2-4]利用系统识别的灵敏度分析理论,了解隧道围岩的特征参数对隧道围岩特性、位移和内力分布以及施工工法多方面进行分析。李迅等[5]结合实际工程,通过对隧道围岩物理力学参数反演,在相同围岩力学参数范围内的数值模拟结果存在较大差异。王兆丰等[6]利用FLAC3D软件对隧道进行模拟,采用隧道范围岩反分析方法和黄金分割方法来确定了该隧道的物理参数。黄初涛等[7]通过反分析方法得到了围岩的参数,并对其进行了有限元弹塑性的正演分析,将遗传算法计算得到的参数逆分析应用于弹塑性正演的分析,平均相对误差为7.33%。苏建伟等[8]对UCODE软件进行编程二次开发,实现UCODE程序与有限元软件间的实时数据交换,验证了反演程序的稳定性和精确性。陈军[9]结合实际工程,利用FLAC3D和MATLAB反演围岩参数,确定隧道围岩力学参数,预测隧道围岩变形和应力。曾永军等[10]利用FLAC3D软件进行位移反分析,结果表明,采用位移反分析获取岩体力学指标是可靠的。吴忠广和吴顺川[11]基于多源数据融合,提出了一种针对深埋硬岩隧道围岩参数的概率反演方法。该方法可实现围岩参数的快速概率反转,更新后的参数可用于硬岩洞施工的安全风险评估和结构可靠性设计。赖若帆等[12]通过正交实验确定了反演参数对拱顶位移的影响顺序,并采用了黄金分割方法对各种影响因素在拱顶位移上的旋转程度进行了逆分析,得到了一个能够满足这种精度的参数。杨建群等[13]采用三维激光扫描技术进行城市周边高速公路隧道的变形测量,建立隧道三维有限元模型,分析围岩的弹性模量、内聚力和内摩擦角。卢斌强等[14]以工程实际来验证位移反分析法在隧道实际工程中的可行性,以围岩弹性模量和黏聚力为反演参数,将反演组合代入FLAC3D数值模拟软件中,计算修改段围岩的沉降变形,并与实际拱顶沉降监测数据进行对比。张秋彬等[15],通过正交试验和Midas数值模拟,得到了软围岩的力学参数,Midas对施工阶段进行了正向分析,分析结果与实测数据进行了比较,来检验其可靠性。孙钱程等[16]建立基于贝叶斯理论的概率反分析方法,为岩土工程参数概率反分析方法的建立提供了思路。基于FLAC3D软件,构建BP神经网络计算分析围岩参数,对隧道物理力学参数进行分析[17-18]。王浩等[19]采用FLAC3D软件模拟隧道施工过程,并基于遗传算法优化的支持向量机,研究高速铁路隧道围岩力学参数反演方法。赵凡等[20]采用FINAL软件对围岩膨胀参数进行反演结果表明,隧道围岩最大膨胀半径与膨胀系数密切相关,两者成正比关系。王述红等[21]为确保围岩力学参数取值的合理性,提出一种新的围岩参数智能反演模型,组成GASA智能模型,证实了反演结果的可靠性。
以上可以看出,有许多学者对隧道反演进行了很多的研究。本文结合云南高速公路,以实际工程为研究背景,利用反分析程序Geo-Inverse.m建立有限元模型,将得到的反演结果与现场实际监测的结果进行对比分析,从而讨论位移反分析法在实际工程中的可行性。
1 工程概况
高速公路全长246.37 km,工程按照全封闭全互通高速公路标准施工,双向四车道,设计车速80 km/h,路基宽度25.5 m。全程沿线存在多处的连拱隧道。工程依托其中一段隧道,隧道总长度为403 m,是一条短隧道,最大埋深为82.210 m。隧道高程为1 305.215~1 386.000 m,相对高程差为80.785 m,属于中切山地貌区。隧道区的主要地层为第四纪斜坡冲积物,含粉质黏土和砾石,下白垩统景星组为泥岩,粉砂岩和石英岩。隧道区域的地表水未开发,隧道的中部是分水岭。从山坡到沟底收集降水,沟壑流入大清河。隧道区的地下水为第四纪孔隙水和基岩裂隙水。隧道围岩岩体参数值由工程的地质情况以及岩石力学的试验结果可以得到,见表1。

表1 隧道岩体参数值
2 参数反演的基本原理
在隧道建设工程中,主要使用通过隧道的开挖与支撑作用过程中检测到的围岩位移反分析围岩的各种物理参数。由于位移反分析中对范围岩输入位移值的计算是受其他地质条件影响最直接、最明显、最全面的一种宏观反映,因此位移反分析获取的各种宏观参数反映了对岩石结构复杂度的总体影响、施工技术方法和隧道建设工程的结构。
2.1 有限元优化反演法的基本原理
为了确保解决方案的稳定性和唯一性,有必要添加一些约束条件来解决反演问题,基本公式为
(1)
式中:Ψ(X)为误差函数,也称为目标函数,X=(x1,x2,…,xm);hi(X)为第i个等式约束函数;gj(X)为第j个不等式约束函数;m为待反演参数个数。
反演问题本质上是通过一般原理由结果推出问题的参数。确定目标函数的引导函数在算法中起到关键性的作用,目标函数复杂会导致不能精确地写出它们的解析度和表达式。因此不太容易得到目标函数的导数。Nelder-Mead法可用来解决这类问题。罚函数法不仅被用来求解一个没有约束优化问题,也可以用来求解一个非线性约束优化的问题变换。
惩戒函数法被认为是一种有效地解决制度约束优化的主要方法,其提出的根本思路就是把约束最优化的问题变为了无约束的极值。其中一种常见的方法就是在原始目标函数中再添加一个约束函数构造而成的“惩罚项”,以便于迫使替换点更容易地接近到可行的区域。如何寻求光滑和准确的简易罚函数表达形式,一直都是现代社会中人们所渴望的目标,准确性与可微程度是判断罚函数时的两大关键课题。
讨论的优化问题见式(1),其中可行解集合为
X={X∈Rm|hi(X)=0,gj(X)≤0},
i=1,2,…,l;j=1,2,…,r
(2)
令
Φ(y)=max2(0,y)
(3)
于是Φ(y)对于y有连续的一阶导数。当y≥0时,Φ′(y)=2y;当y<0时,Φ′(y)=0。再令
S(X)=∑[hi(X)]2+∑Φ[gj(X)]
(4)
由式(4)可知,S(X)≥0且S(X)=0的充要条件是hi(X)=0(i=1,2,…,l)及gj(X)≤0(j=1,2,…,r)。于是式(1)所示优化问题的解X*满足S(X*)=0。
对于式(1)所示的约束问题,精确罚函数可表示为
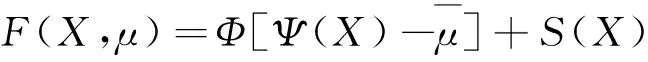
(5)
对于新的罚函数,其优化程序为
(6)
Nelder-Mead方法是一种用于寻找多维函数极值的算法,它不用再计算其中的函数导。适用于查找变量较少的方程极值。本方法的思路是:首先通过给出一些等待求逆参数的初始值,计算得到目标函数的值,并根据这些函数值与时间长度比之间的相关性,找出目标函数的上升和下降方向。然后找出任意一组降序调整的参数值,计算出这组降序调整的参数的目标函数值,并将新值加到其中与原始参考值进行比较,从而寻找得到该组函数的一个新降序,直至满足要求。
若有m个参数待反演,即x1,x2,…,xm。空间中一点参数为m维空间,m+1组参数表示m维空间m+1个点P0,P1,P2,…,Pm,这m+1个点要线性独立的话,就会形成一个单纯形,取作
(7)
分别计算它们的对应目标函数值,依大小排列依次为FH、FG、FL;对应的点依次为PH、PG、PL。除了PH外,计算其余点的质心,记为PC,计算式为
(8)
PC点的每一分量为
(9)
再求出PH的反射点PR为
PR=2PC-PH
(10)
反射点PR的每一分量为
xjR=2xjC-xjH,j=1,2,…,m
(11)
算出PR点的对应的目标函数值FR。
如果FR≥FG,按下式压缩:
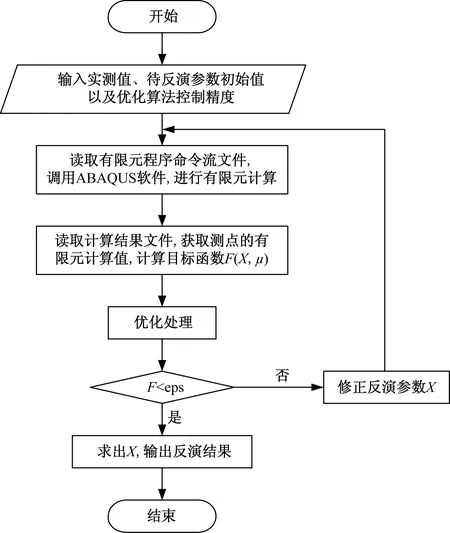
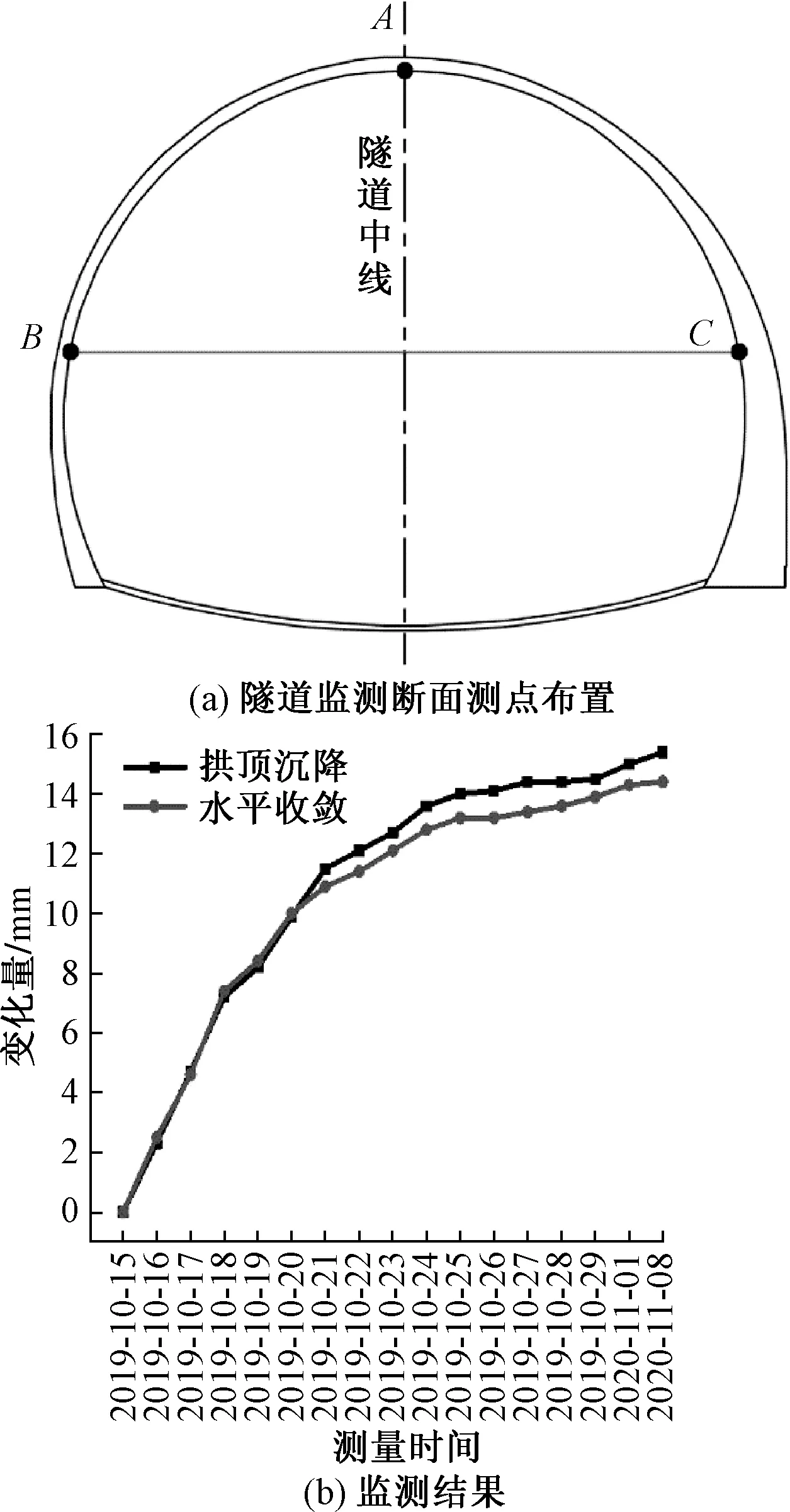
PS=(1-x)PR+xPH,0 (12) 如果FR≤FG,按下式扩张: PE=(1-ϑ)PH+ϑPR,ϑ>1 (13) 计算函数FE,若FE≥FG,则扩张失败,取PR为PS,FS=FR,若FE≤FG,说明扩张成功,取PE为PS,FS=FE。 在找出新的点PS后, 比较FS与FG,若FS≥FG,则减小原来的单纯形,若FS (14) 由PMi和PL组成新的单纯形,再继续搜索。 基于以上理论和方法,基于ABAQUS,以MATLAB语言作为平台的大规模有限元软件程序,结合精确惩罚函数法和Nelson-Mead算法,编制出了优化后的逆分析程序Geo-Inverse.m。逆分析过程Geo-Inverse.m的框图设计如图1所示。 图1 岩土体参数反演程序框图 程序Geo-Inverse.m具体实施步骤如下: 1)将ABAQUS命令流在MATLAB中运行并计算。 2)调用计算结果,并使其计算目标函数。 3)对目标函数利用Nelder-Mead算法进行优化。 4)修改反演参数。 编制的Geo-Inverse.m程序可进行反复精确的计算,能不断修正反演参数,进行优化处理,达到精度要求后,再输出反演结果。用得到的反演结果与实测参数进行对比,给出隧道围岩的最优参数值,可为后续施工提供帮助。 隧道监测断面共设计3个变形观测点,A点为拱顶沉降观测点,测线BC为水平收敛观测线。隧道监测断面测点布置和监测结果如图2所示。 图2 隧道监测断面测点布置及监测结果 通过三点监测出的变化量与在从开始监测到2019年10月20日之前水平收敛和拱顶沉降的变化量基本相同,但此之后拱顶沉降的变化量要明显比水平收敛的变化量大,其最大峰值分别为15.4 mm和14.4 mm。 同时,用本文所提到的方法,对隧道进行了计算。以隧道ZK212+896断面沉降观测数据与水平收敛观测数据作为依据,岩土体参数为E和ν,共2个力学参数作为反演目标。反演得到岩体参数结果和反演结果与实测结果对比,分别见表2和表3。 表2 隧道监测断面有限元反演结果 表3 隧道监测断面反演结果与实测结果对比 弹性模量和泊松比分别取1.50 GPa和0.35,反演得到拱顶沉降和水平收敛值分别为15.81 mm和14.68 mm,与实测结果相对比误差较小,误差分别为0.4 mm和0.28 mm,可以看出,反演结果的大小和趋势与测量结果基本一致。 以云南高速公路隧道为依托,通过研制的Geo-Inverse.m程序系统,建立数值模型,利用位移反分析法对隧道的围岩进行分析,并与实际监测结果进行对比,从而得到以下结论: 1)根据隧道拱顶沉降和水平收敛的监测资料,采用有限元反分析方法,得出隧道围岩基本参数。推荐值为弹性模量1.50 GPa,泊松比0.35;内聚力350 kPa。 2)现场测量和隧道变形有限元反演结果表明,隧道段围岩相对较弱,开挖后变形相对较大,但经支护后能够在短期内达到稳定。2.2 程序研制
3 隧道围岩变形监测及反演结果


4 结论
