考虑土石界面渗透性的土石混合体渗流有限元模拟
2022-07-08何玲丽田东方王世梅
何玲丽,田东方,王世梅,陈 勇
(1.水利与环境国家级实验教学示范中心,湖北 宜昌 443002;2.三峡大学水利与环境学院,湖北 宜昌 443002;3.三峡库区地质灾害省部共建教育部重点实验室,湖北 宜昌 443002;4.三峡大学土木与建筑学院,湖北 宜昌 443002)
1 研究背景
土石混合体(SRM)是指第四纪以来形成的,由具有一定工程尺度、强度较高的岩块、细粒土体及孔隙构成且具有一定含石量的极端不均匀松散岩土介质系统[1]。这类介质在我国各地广泛分布于边坡、地基及地下工程中,还经常作为工程材料应用于大坝、岸堤、路基、机场等。以SRM的细观结构(即其中块石的形状、尺寸、分布等信息)为基础,通过渗流数值模拟可以确定水分在土体与块石中的运移过程。以此为基础,可开展渗透数值实验,揭示细观结构对SRM渗透特征的影响,也可从细观尺度研究土石混合体内部变形破坏过程,有助于探索土石混合体破坏机制。
目前,基于细观结构的渗流模拟,多将SRM视为土体和块石构成的二元介质,采用达西定律描述土体和块石的渗流,利用有限元实现数值模拟,如徐文杰等[2]和Yan等[3]的研究。数值实验表明,SRM渗透系数受含石率影响较大,且随含石率的增大而单调递减;同时,由于土体和块石的渗流符合达西定律,故SRM的渗流也符合达西定律。
然而,实验表明SRM的渗透系数随含石率的增大并非单调递减,而是先降后增[4-5],如图1a所示;此外,SRM的渗透速度是水力梯度的幂函数[6-7],如图1b所示。从图1a可见,现有的数值模拟不能很好地反映SRM的渗透特征。这可能是因为未考虑土石界面渗透性而造成的。土石界面通常是SRM中的薄弱环节和应力集中的部位,这将使得土石界面附近土体的孔隙分布与基质土体存在一定差异而容易形成集中渗流通道。因此,土石界面的渗透性必须加以考虑。
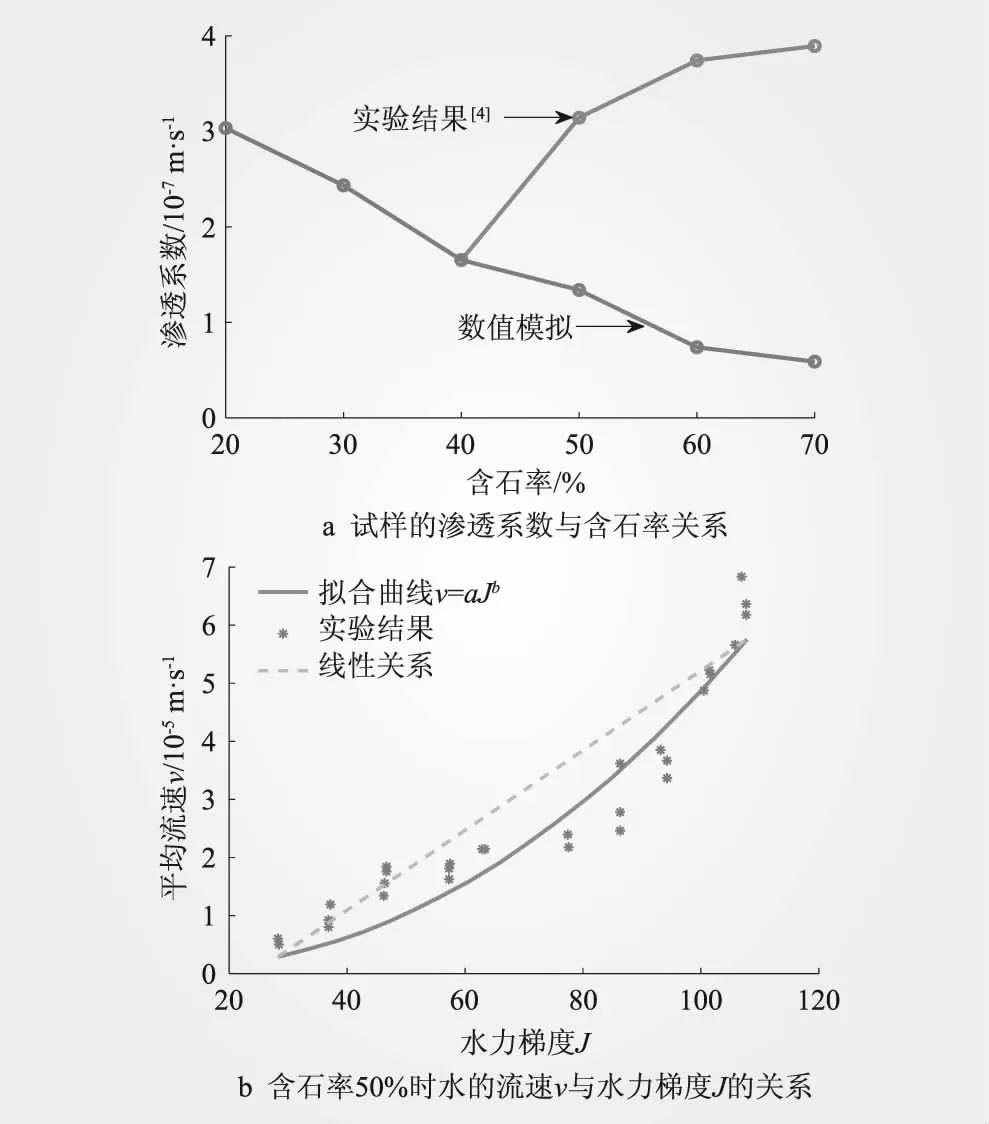
图1 土石混合体渗透特性
由于土体和块石渗流符合达西定律,那么SRM渗透速度与水力梯度之间的幂函数关系,应由土石界面的渗流引起。结合文献[4,6]的实验规律,本文假定界面流量是水力梯度的幂函数。
综上,基于SRM细观结构进行渗流数值模拟时,现有方法未考虑土石界面的渗透性,不能正确反映SRM的渗透特性。为此,本文忽略岩块的渗透性,将SRM视为由土体和土石界面构成的二元介质,假定土体渗流为二维达西流,土石界面为一维渗流且流量是水力梯度的幂函数,基于有限元法实现考虑土石界面渗透性的SRM渗流数值模拟。
2 模型的构建
2.1 控制方程
SRM渗流模拟区域如图2所示,考虑到岩块的渗透性远小于土体,故忽略岩块的渗透性;则渗流求解域为土体区域Ω,以及M条土石界面Γr,r=1,2,…,M。假定土体各向同性且为二维达西渗流;土石界面为一维渗流。
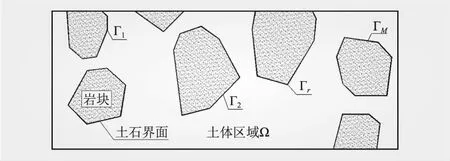
图2 SRM渗流模拟区域示意
土体渗流方程为
(1)
式中,H为总水头;ks为土体饱和渗透系数;x,y为坐标,位于水平面内。
在定水头边界ΓH上
(2)
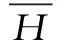
沿任意一条土石界面,建立弧坐标l;设在第r条界面Γr上,从土体到界面的流量为qi(l),则
(3)
式中,l为沿界面的弧长坐标;nx、ny分别为Γr外法线单位向量在x、y轴的分量(土体为内部区域)。
记q(l)为土石界面Γr的沿程流量,假定只考虑从土体流入界面的水量,根据水量守恒有
∂q/∂l=qi
(4)
本文假定q为水力梯度J的幂函数,则
q=aJb
(5)
式中,a、b为土石界面渗透参数。
记h(l)为土石界面Γr上的沿程水头,则J=-∂h/∂l,令kq=aJb-1,结合式(4)、(5)有
(6)
2.2 方程的Garlerkin弱解形式
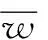
(7)
由格林公式可知
(8)
将式(8)代入式(7),引入边界条件(3)得
(9)
式(6)的加权余量格式为
(10)
根据格林公式,式(10)左端变为
(11)
式(11)右端第一项,当Γr自行封闭时(如图2中的Γ2),其值为0;当Γr不封闭时(如图2中的Γ1),其值根据边界条件式(2)确定。这一条件在有限元求解时,通过引入定水头边界得以满足。故该项略去不写。
将式(10)引入式(11)后,可改写为
(12)
2.3 模型的有限元求解
用有限元求解式(9)和式(12)时,可借鉴岩体渗流问题中的两域渗流模型,即分别求解两场(H和h)、迭代确定qi。但土石界面数量较多,迭代将带来较大的计算开销以及收敛问题。为此,本文假定水头在土体与界面接触处是连续的,即在任意界面Γr上,h=H。将式(9)与式(12)左右对应相加消去qi,可得
(13)
如图3所示,本文采用适应性强的三角形单元离散Ω;土石界面将被离散为两节点线单元,节点整体编号与三角形单元共用。
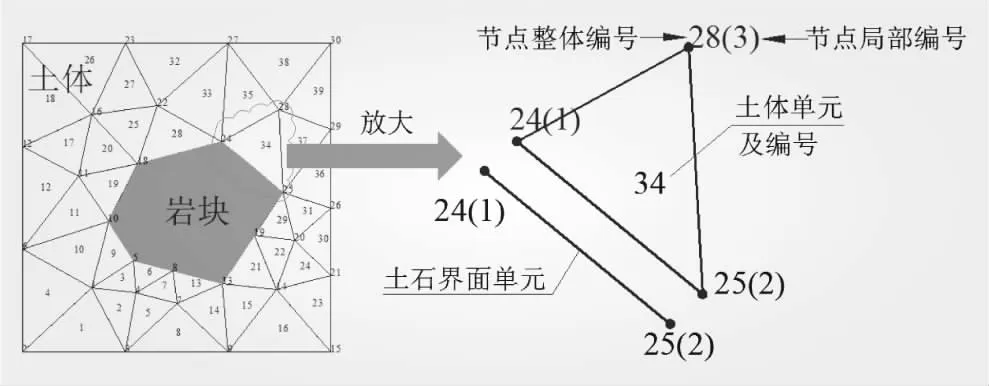
图3 土体和界面单元示意
三角形单元e内的He、线单元τ上的Hτ采用单元节点水头Hi、Hm的线性插值,即
(14)
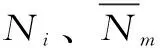
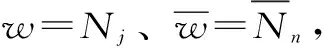
([D]+[R]){H}={f}
(15)
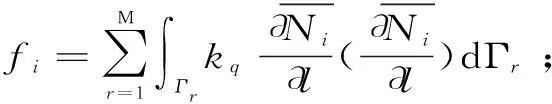
本文采用增量法[8]求解式(15)。
3 模型验证
3.2 算例一
算例一与徐文杰等[2]的渗透数值实验进行对比。试样细观结构见文献[2]中图6;本文计算时,不考虑块石渗透性,土石界面渗透参数取a=b=0,其他条件同文献[2]。对比结果见表1,其中,ku为试样等效渗透系数与土体渗透系数之比。
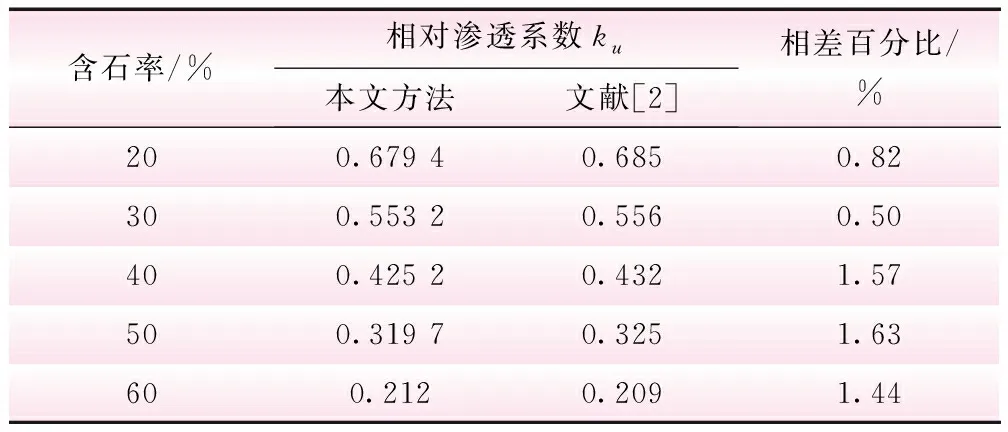
表1 不同含石率相对渗透系数ku的对比
由表1可知,本文与文献[2]结果相差均小于2%,表明本文方法和程序可以模拟不考虑界面渗透性的情形。由于块石透水性相比土体而言通常小几个数量级,而块石数量将随含石率增大而增多从而降低试样渗透性。因此,当只考虑土体和块石的渗透性时,SRM的渗透性必然随块石的增多而减小。
3.3 算例二
本算例与王宇等[4,6]的SRM渗透性实验进行对比。实验试样尺寸、边界条件如图4所示。试样中块石粒径2~5 mm。文献[6]中试样的含石率分别为20%、30%、40%、50%、60%、70%;由于未提供试样细观结构,本文利用文献[9]方法生成相应试样的细观结构;每个试样中块石粒径分别为2、3、4、5 mm,各粒径块石的体积分数均为0.25。限于篇幅,图4只展示了含石率为20%和70%时试样的细观结构。
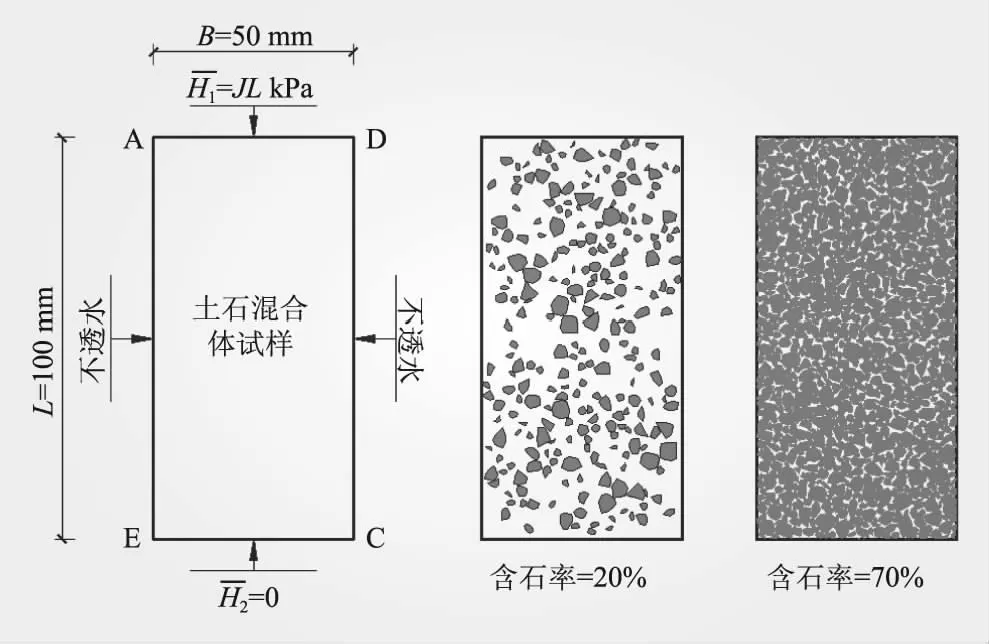
图4 算例二的试样尺寸、边界及细观结构(灰色区域代表岩块)
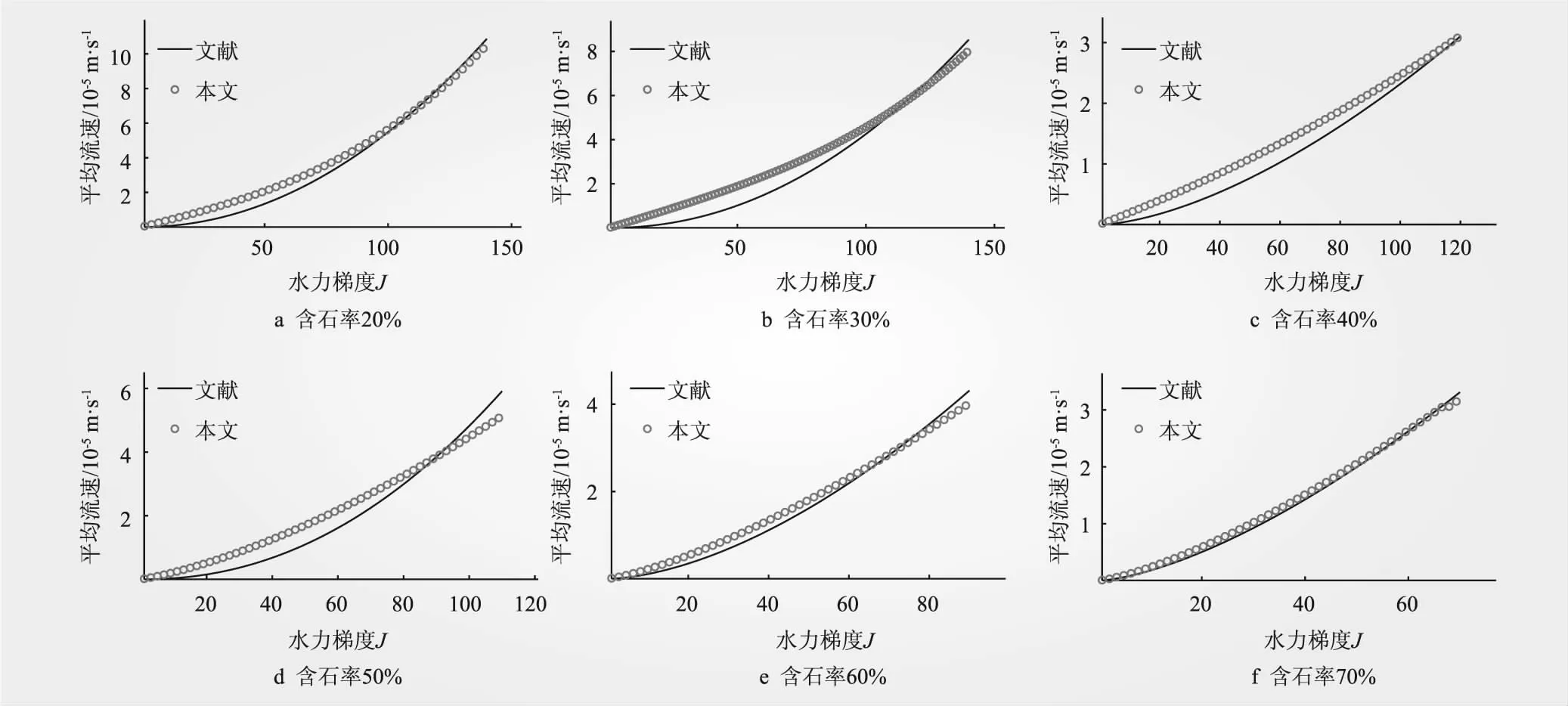
图5 平均流速-水力梯度关系对比
数值模拟时,土体ks=6.17×10-7m·s-1,土石界面渗透参数a、b通过试算确定,具体取值见表2。

表2 算例二计算参数及实验结果的偏差
数值模拟所得试样中的平均流速与文献[6]的对比见图5。本文定义err描述某一含石率时的n组模拟和实验数据之间的偏差,按式(16)计算,即
(16)
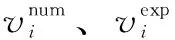
从图5可以看出,本文方法可再现SRM的非达西流特性;从表2所列误差err来看,含石率较高(如60%、70%)时,模拟结果与实验结果较接近,含石率为30%~50%时偏差较大。
文献[6]给出了水力梯度等于50时,渗透系数随含石率的变化规律。数值模拟所得渗透系数与文献[6]对比见表3。
由表3可知,尽管有时数值模拟和实验结果相差较大(最大约35%),但本文方法能再现SRM试样的渗透性随含石率的增大而先降后增的现象。
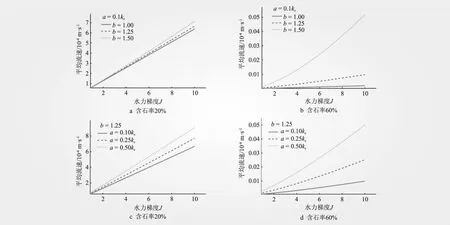
图6 试样平均流速与水力梯度的关系
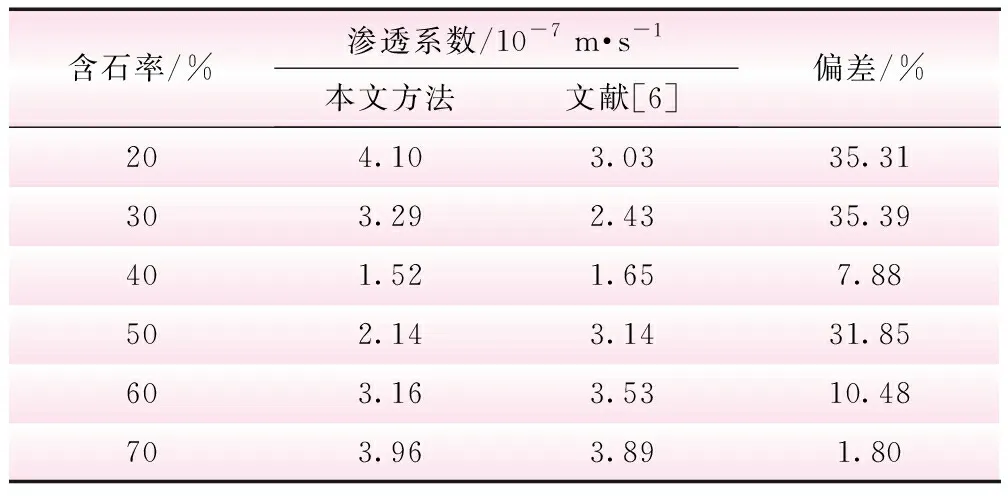
表3 渗透系数结果对比
4 土石界面渗透参数影响分析
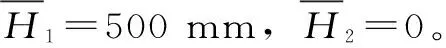
图6为a、b取不同数值时,试样平均流速与水力梯度的关系。由图6可知,b值越大,非线性越强;a值越大,渗透速度越大;含石率越高,渗透特性对参数变化越敏感,即随a值的增加渗透速度增大得更快,随b值的增加非线性更强。这是因为含石率越大,土石界面数量越多,对试样渗透特性影响越大。
本节初步研究了土石界面渗透参数(a、b)对SRM渗透性的影响。其他因素的影响将在后续研究中进一步考虑,例如土石界面流量与水力梯度的其他函数形式、块石形状及分布的随机性等。
5 结 论
(1)将SRM视为由土体和土石界面构成的二元介质,假定土体渗流为二维达西流,土石界面为一维渗流且流量是水力梯度的幂函数,水头在土体与土石界面处连续;从而避免采用迭代方法确定土体和界面间的流量交换,构建了土体和土石界面渗流场同步求解有限元模型,实现了考虑土石界面渗透性的土石混合体渗流模拟。
(2)算例验证表明,所建方法可模拟不考虑或考虑土石界面渗透性的情形。当考虑土石界面渗透性时,本文方法可较好地再现土石混合体渗透性随含石率增大先降后增以及渗流速度与水力梯度的非线性关系等实验现象。
(3)渗透数值实验表明,土石界面渗透参数对SRM渗透特性影响为:a值越大,渗透速度越大;b值越大,非线性越强;含石率越高,SRM渗透特性对参数的变化越敏感。
