小型均质土石坝渗流分析及变形危害防护

杨青辉

(自贡市水利电力建筑勘测设计院，四川 自贡，643000)

土石坝是由土、砂石料等材料建成的坝，是历史最悠久、数量最多的坝型。我国小型水库众多，20世纪六七十年代建设的小型水库，其大坝多为土石坝，受历史条件、水库设计、施工技术以及运行管理等因素的制约，目前大多已成病险水库。对小型均质土石坝建立二维稳定渗流的有限元表达，计算结果表明均质土石坝的边坡抗滑稳定性受大坝渗流的影响很大。在大坝成功蓄水后，由于大坝上下游水头差，均质土坝坝体、坝肩及坝基会产生地下渗流，若防渗设施设置不当或被破坏，则渗透压力会造成渗流破坏，此外，坝体浸润线以下坝体填料处于饱和状态，抗剪强度指标降低会降低下坝坡的抗滑稳定系数[1]。因渗流破坏而造成土石坝失事的比例占到35%左右，对土石坝进行渗流分析，可了解土石坝渗漏机理，可有效布设防渗措施。

1 土石坝的渗流特性

均质土石坝基本为无压渗流，渗流状态可分为稳定渗流和不稳定渗流。稳定渗流主要在水库在正常蓄水位时；不稳定渗流主要在水库泄洪及对大坝整治时降低水位至死水位时，此时坝体内的浸润面会随着水位的下降而变化，需要考虑时间因素对坝坡稳定的影响。本文主要研究土石坝稳定渗流状态。土石坝中的渗流流速v和坡降的J的关系一般符合如下的规律：

ν=KJ1/β

(1)

式中：K为渗透系数；β为参量，层流时为1～1.1，紊流时为2，过渡流态时为1.1～1.85[2]。

在本次小型均质土石坝渗流分析中，假定渗流流速和坡降的关系符合达西定律(β=1)，坝体内各点和各个方向的渗透系数K是相同的[2-3]。对于河谷中的小型土石坝，一般采用二维渗流分析就可满足工程要求[2-3]。本次二维渗流分析的基本方程。

根据达西定律及流体力学的连续方程条件：

(2)

(3)

由式(2)及式(3)可得二维渗流方程：

(4)

上述三式中：νx、νy为x向和y向的渗流流速；Kx、Ky为x向和y向的渗透系数，并假定Kx和Ky不随坐标而变化；H为渗流场中某一点的渗压水头。

由于土石坝坝体填筑的施工为分层夯实，实际上坝体的渗透系数不是均匀的，水平向渗透系数Kx和竖直向的渗透系数Ky并不相同，其差别可达10倍以上，因此，渗透不均匀性不能忽略[4]。将式(4)进行坐标变换：

(5)

变换后的坐标系XY中：

(6)

可使计算得到很大程度的简化，渗流流速仍然符合达西定律，但需将Kx和Ky代之以K=(KxKy)0.5，最后再将XY坐标系中的计算结果按式(5)转回xy坐标系中[2，5]。

2 水力学渗流分析方法

2.1 不透水地基均质土坝

2.1.1 下游无排水棱体

浸润线位置可以利用水力学的方法近似确定，并计算出渗流流量、平均流速及坡降。水力学方法计算渗流需对土石坝进行相应的假定：等势线和流线均缓慢变化，渗流是缓变流动，渗流区可用矩形断面的渗流场模拟。土石坝全断面渗流(等效渗流长度为L)水力坡降为J=(H1-H2)/L，平均过渗断面为A=(H1+H2)/L，利用达西定律可推导出均质土石坝单宽流量q为：

(7)

同理可推导出计算点的渗流水深y为：

(8)

上述二式中：H1、H2为上、下游水深；L为渗流区长度；x为计算点至上游起始截面的距离。

对典型土石坝剖面分析后，可将其剖面分成上游水位以下的三角形、中间段、下游浸润线以下的三角形，如图1所示。

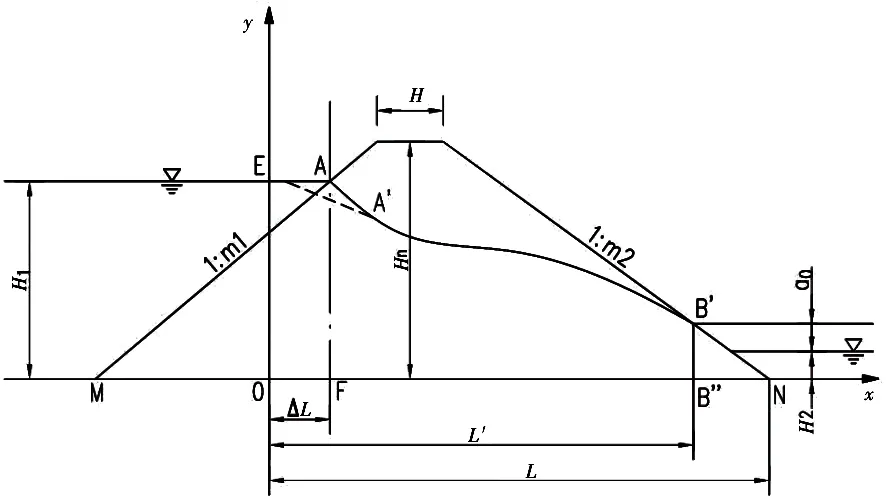
图1 不透水地基均质土坝计算

上游三角形坝体可用等效矩形体代替，其矩形宽度ΔL根据电拟试验成果，可近似用下式计算：

(9)

式中：m1为上游坝坡系数，边坡时可取其平均值。

将等效矩形体和中间段作为整体(参见图1，E0B′B″段)，设渗透系数为K，根据达西定律和渐变流定理，通过各竖直截面的渗透流量为：

(10)

图2 不透水地基均质土坝下游坝脚计算

(11)

根据渗流连续的边界条件，q1=q2=q，联立式(10)与式(11)或用试算法可求得a0和q值。

2.1.2 下游有排水棱体

因排水棱体渗透系数远大于坝体渗透系数，故浸润线将要进入排水体时，下降加快，进入排水体后骤降。由式(10)可知坝体内的浸润线为抛物线，因此，可以近似假定排水棱体内坡脚与下游水面交点为抛物线的焦点，近似把H2高度内坝体认为不透水，浸润线进入排水棱体后与下游水面的交点为抛物线顶点，并建立坐标系，如图3所示。

图3 有排水棱体不透水地基均质土坝计算

设抛物线的标准方程为有y2=2Ax+B，当x=0时，y=h0；由抛物线的性质可知当x=Lg=-h0/2时，y=0，因此，可以求出抛物线的方程为y2=2h0x+h02。可通过边界条件x=L，y=H1-H2求得h0=(L2-(H1-H2)2)0.5-L。参考式(10)的推导可得渗流量为：

(12)

式(12)计算出来的渗流量与实际情况有所差别，算出的浸润线比实际偏高，因此，在计算坝坡稳定时是偏安全的。

2.2 透水地基均质土坝

透水地基均质土坝渗流量计算可看成不透水地基土石坝通过坝体的渗流量和把坝体当不透水体计算的坝基有压渗流量之和。坝体不透水计算坝基内有压渗流量q2：

(13)

式中：T、KT为坝基透水层深度及其渗透系数；L0为坝底宽度(不包括透水料部分)。

2.3 土石坝渗流分析常用工程软件

Autobank、ANSYS、Geostudio等基于二维渗流方程开发的渗流计算软件，能较精确地计算小型均质土石坝的渗流量、渗透坡降及渗流流速等参数，在小型均质土坝的除险加固设计中得到了广泛的应用。

3 渗流变形及其防护

3.1 土石坝渗透变形主要类型

我国早期的小型均质土石坝由于其构成材料主要是土料、石料或是土石混合料。坝体长期在水中浸泡，水分会顺着土石料颗粒间缝隙进行流动，微小的渗透不会导致坝体变形，但如果渗流量很大，当水力坡降大于土体破坏时的临界坡降时就会使坝体产生变形进而可能发展成溃坝事故。下游坝坡脚处的水力坡降是进行土石坝渗流计算时需重点关注的地方，因为该处发生渗透变形可能导致坝下游坡面产生局部滑动。土石坝的渗透变形主要有接触冲刷、流土、管涌和接触流土等四种情形[2]。

3.2 渗透变形原因简析

土体中的渗透压力大小和水力坡降成正比，其方向与渗透方向一致。当土颗粒的渗透压力大于其受到的重力或者阻力时，土体就要发生浮起或者遭到破坏。当向上的渗透压力克服了重力时，土颗粒间的有效应力为零，颗粒集体发生悬浮移动的现象称为流土现象。该现象常发生在颗粒级配均匀土层中，一般为突发性的，对工程危害大。

流土现象的发生取决于渗透压力的大小、土颗粒级配、密度及土体的透水性等。当刚开始发生流土现象时的水力坡降称为临界水力坡降icr，即渗透压力γwi等于土的浮重度γ′时，土体处在临界状态，因此，临界水力坡降icr为：

(14)

式中：ds为土颗粒比重；n为土体孔隙率。

临界水力坡降与土的特性密切相关，不均匀系数越大，icr值越小；土中细颗粒含量高，icr值增大；土的渗透系数越大，icr值越小。

3.3 渗透变形的防治

小型均质土石坝的渗透变形主要表现形式为流体和接触冲刷。

对上述渗透变形的防治思路或者方法为：减小或者消除水头差，如设置反滤减压井或反滤排水沟，降低渗流出口处的渗透压力，有效排除坝基渗水；在渗流出口处用透水材料覆盖压重以平衡渗透压力；在土体颗粒粒径相差较大时设置过渡层并设置反滤层[6]。

4 结论

(1)利用水力学的方法近似分析小型均质土石坝的渗流可知，其渗流量与渗透系数及上游水头成正比，与下游水头及渗流长度成反比。

(2)小型均质土石坝在下游坡脚设置排水棱体可有效降低浸润线及渗流量，有利于大坝坝坡稳定。

(3)坝体某处的水力坡降大于该处的临界水力坡降时，会发生渗透破坏；临界水力坡降的影响因素包括不均匀系数、细颗粒含量、渗透系数等。

(4)小型均质土石坝的渗透变形防治办法为：减小或者消除水头差；在可能渗流出口处设盖重，并设置反滤排水；土体颗粒粒径相差较大时设置过渡层并设置反滤层。