一种自适应的密度峰值聚类算法
2022-07-08马淑华尤海荣
马淑华, 尤海荣, 唐 亮, 何 平
(东北大学秦皇岛分校 控制工程学院, 河北 秦皇岛 066004)
随着计算机技术的发展,数据和信息呈现井喷式增加,使得大数据技术日趋成熟.其中数据挖掘技术是在海量的数据中挖掘有价值的信息,使数据实现价值最大化,在当今时代显得尤为重要.聚类算法是数据挖掘技术中的一个重要领域,用以描述事物之间的差异及相似性,因此对聚类算法进行研究具有十分重要的价值和意义.当前的聚类算法大致可分为以下6类:
1) 基于划分的聚类算法.基于划分的聚类算法原理是首先创建k个类别,挑选初始中心后根据启发式算法进行更新迭代从而获取最优效果[1].这类算法中最常见的就是K-means算法,后续又演变出K-medoids,K-modes,K-medians,kernel K-means等算法[2-7].这类算法简单高效,但是容易出现局部最优的情况,并且对初始值和噪声十分敏感.
2) 基于层次的聚类算法.基于层次的聚类算法分为合并和分裂两种.前者的基本原理是从底层开始,合并相似的聚类构建上一层聚类,直到所有数据都合并成一层聚类时终止.后者恰恰相反,从一类包含所有数据的类别开始,即从顶层开始,然后从上而下进行类别分裂,直到一个数据点为一个类别结束[8].常见的此类算法有平衡迭代削减聚类(BIRCH)算法等[9].这类算法可解释性好,但是时间复杂度十分高.
3) 基于网络的聚类算法.此类算法原理比较简单,就是将数据划分为网格空间,然后判断网格空间是否符合高密度的条件,如果是,将相邻的两个高密度单元定为一簇[10].常见的基于网格的聚类算法有数据信息网格(STING)算法、集群查询(CLIQUE)算法等[11].此类算法速度很快,但其对参数敏感,并且不适用于不规则的数据.
4) 基于模型的聚类算法.基于模型的聚类算法首先为数据假设了一个模型,然后寻找最佳拟合模型,大多采用基于概率的模型[12].这一类别常用的算法有高斯混合模型[13].此类算法对类的划分不是十分死板,但是执行效率不高.
5) 基于模糊的聚类算法.基于模糊的聚类算法是根据隶属度对数据进行划分的,克服了传统聚类算法非此即彼的缺点,但是该算法依赖已有的初始聚类中心,因此还需要其他聚类算法进行配合[14].常见的此类算法有模糊C均值聚类(FCM)算法[15].
6) 基于密度的聚类算法.基于密度的聚类算法基本原理是画圈,基于圈的半径和圈的最小容量两个参数进行划分[16].此类算法中最常用的算法是带噪声的基于密度的应用程序空间聚类(DBSCAN)[17],最典型的基于密度的聚类算法是密度峰值聚类(density peak clustering, DPC)算法[18].此类算法可以应用于不规则形状的聚类,并且对噪声不敏感,但是聚类结果受参数影响比较大.
基于以上分析可以得知,基于密度的聚类算法性能最好,但是受参数影响比较大,聚类效果的好坏取决于参数选取是否精确.因此本文对密度峰值聚类算法进行了参数的自适应改进,从而进一步实现聚类算法的优化.
1 DPC算法
密度峰值聚类算法是基于密度的聚类算法,其基本思想是聚类中心在其邻域内具有最高的密度值,并且与其他聚类中心距离较远.该算法基于以下两个参量:局部密度ρi和相对距离δi[18].
定义1局部密度ρi.局部密度根据数据的离散和连续分为截断核和高斯核两种计算方式,其中截断核适用于离散数据,计算公式为
ρi=∑j≠iχ(dij-dc) .
(1)
其中:i,j代表数据集中的两个点;ρi代表第i个点的密度;dij代表第i个点和第j个点的欧氏距离;dc代表截断距离.
χ(x)定义如下:
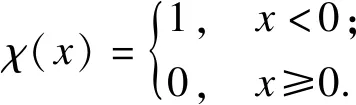
(2)
高斯核适用于连续数据,计算公式为
(3)
定义2相对距离δi:
(4)
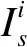
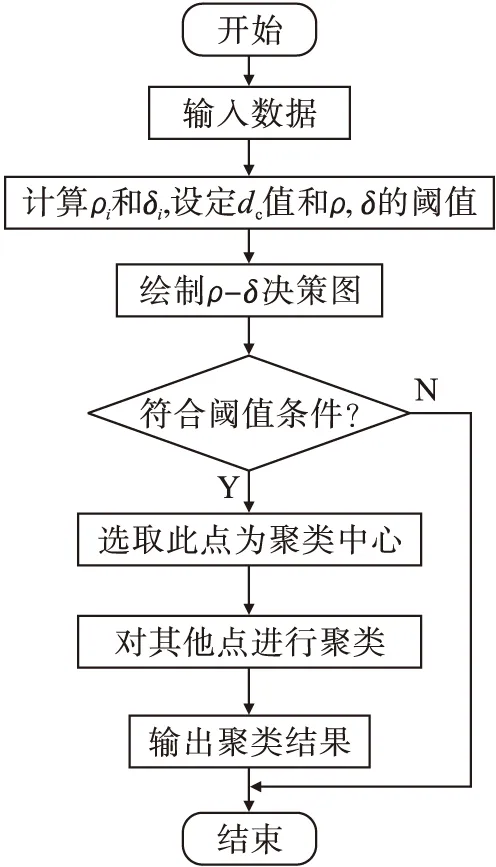
图1 DPC算法的流程图Fig.1 The flowchart of DPC algorithm
2 ADPC算法
传统的密度峰值聚类算法对参数依赖性比较强,通常情况下密度峰值聚类算法依靠人工选定聚类中心和截断距离dc值,比较耗费时间,并且在参数选择不恰当时,聚类效果与预期效果大相径庭.因此,本文对DPC算法的聚类中心的选择和dc参数进行了自适应改进.
2.1 聚类中心的自适应选择
首先,设计了一个综合考虑局部密度ρi和相对距离δi的参数μi:
μi=ρilgδi.
(5)
根据DPC算法的特征,聚类中心与其他点相比具有较大的ρi和δi,本文选取对数函数来定义μi,因为聚类中心通常具有较大的局部密度ρi和相对距离δi,因此用式(5)来加大聚类中心的μi与其他点μi值的差异,得到μi之后,将μi值从大到小进行排序,然后计算μi值的下降趋势,定义如下.
定义3下降趋势:
(6)
其中:μi是当前的μ值;μi-1和μi+1分别代表前一时刻和后一时刻的μ值.
获取到下降趋势之后,取下降趋势最大的点及前面的几个点作为聚类中心.
2.2 dc参数的自适应选择
DPC算法通常是经过实验验证或者凭借经验获得dc值,具有很大的不确定性,通常好的聚类算法划分的同种类别的差异较小,因此选取dc值可以根据综合衡量元素差异来获取,本文正是采用衡量元素差距的参数——基尼系数去约束dc值,即求取基尼系数最小时的dc值.
定义4基尼系数G.传统的基尼系数是用来衡量一个国家的居民收入差距的[19],本文采用该指标衡量聚类结果中每种类别内元素的差异.定义如下:
(7)
其中:n代表数据集S中的样本个数;pi为i点的ρi×δi占所有点的比例,pi取值如下:
(8)
根据式(7)取最小值时的dc值作为最终的dc值,代替经验法或实验验证,从而达到自适应选取参数的效果.
2.3 ADPC算法整体流程
ADPC算法过程如表1所示.

表1 自适应密度峰值聚类算法过程Table 1 ADPC algorithm process
3 结果及评价
所有实验均在Lenovo-Y7000P笔记本上进行,操作系统为Windows 10,Intel i5-9300H CPU,实验平台为Matlab R2018a.
3.1 数据集和评价指标
为了避免实验结果的偶然性,本文选取了6组典型的聚类数据集进行了ADPC算法测试,包括:D31,Data1,Data2,Aggregation,Spiral,Fish数据集.重点对D31数据集聚类过程进行了详细分析,对其数据集的聚类效果进行了展示,并且与DPC聚类算法以及最常用的K-means聚类算法进行了聚类效果对比.
本文采用常用的评估聚类效果的3项指标进行衡量,分别是调整兰德指数ARI、标准化互信息NMI以及准确度AC.
3.2 ADPC算法聚类过程实现
以D31数据集为例对ADPC算法进行详细说明及分析:
1) 首先将dc=1作为初始值,计算D31数据集的局部密度ρi和相对距离δi,并绘制决策图,如图2所示.
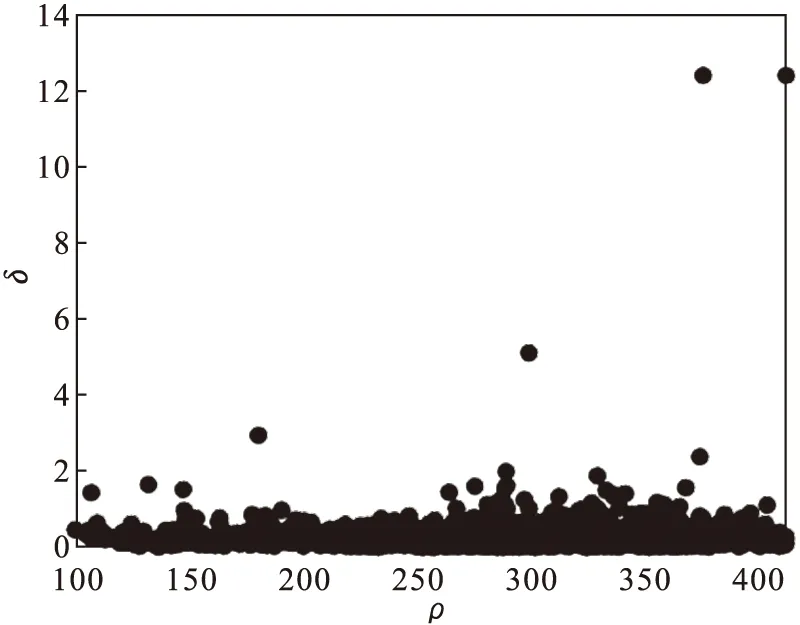
图2 D31数据集的决策图Fig.2 Decision graph of D31 dataset
2) 改变dc的值,并计算每个dc值对应的基尼系数,绘制dc和基尼系数的关系图,如图3所示.
3) 根据图3,当dc=2时,基尼系数具有最小值,因此令dc=2,重新绘制ρ-δ分布图,新的分布图如图4所示,可以看出,新的分布图具有更高的规律性,具有较大的局部密度ρi和相对距离δi的点分布比较集中.
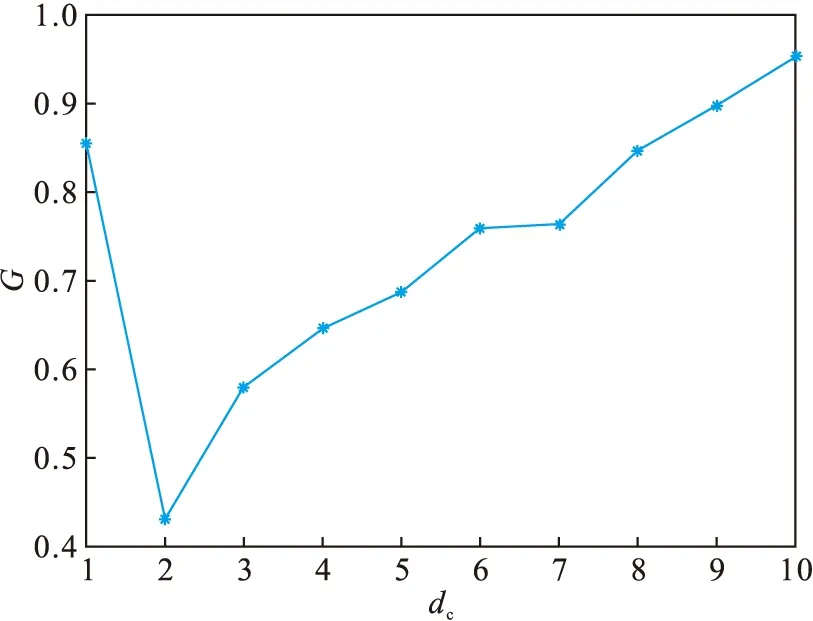
图3 基尼系数和dc的关系图Fig.3 Gini coefficient and dc relationship diagram
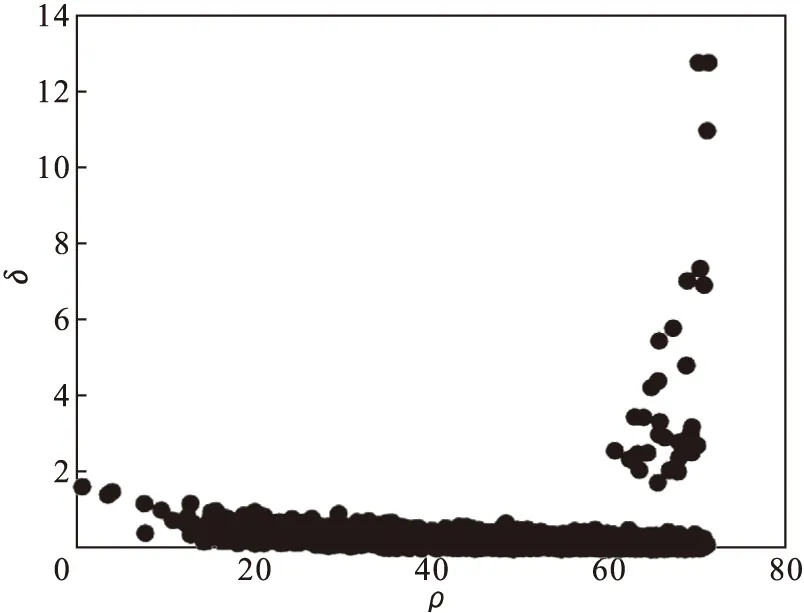
图4 改进后的决策图Fig.4 Improved decision graph
4) 根据式(5)计算μi的值,并将其降序排列,绘制μi降序图,如图5所示.根据式(6)下降趋势的定义,计算μi对应的下降趋势值,并绘制下降趋势图如图6所示,图6中第31个点具有最高的下降趋势,因此选取前31个点作为聚类中心点,聚类中心的选择如图7所示.
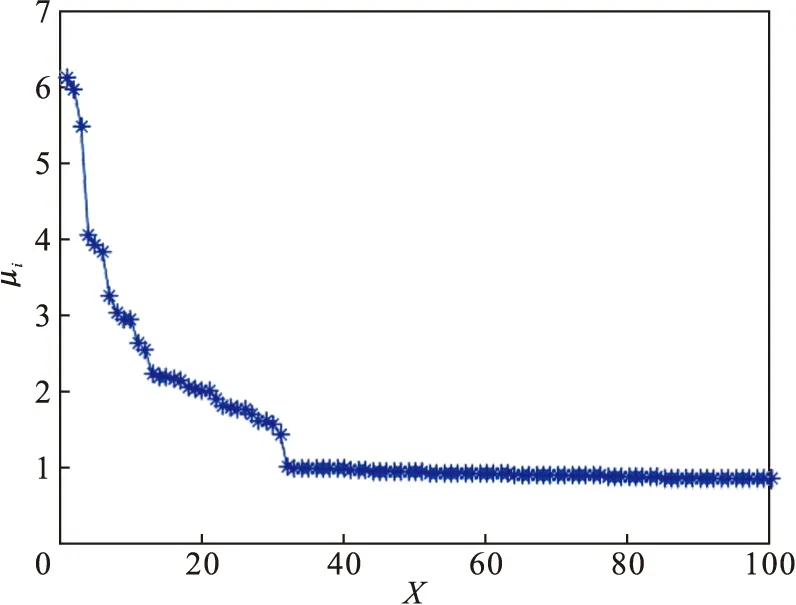
图5 μi值的分布Fig.5 The values distribution of μi
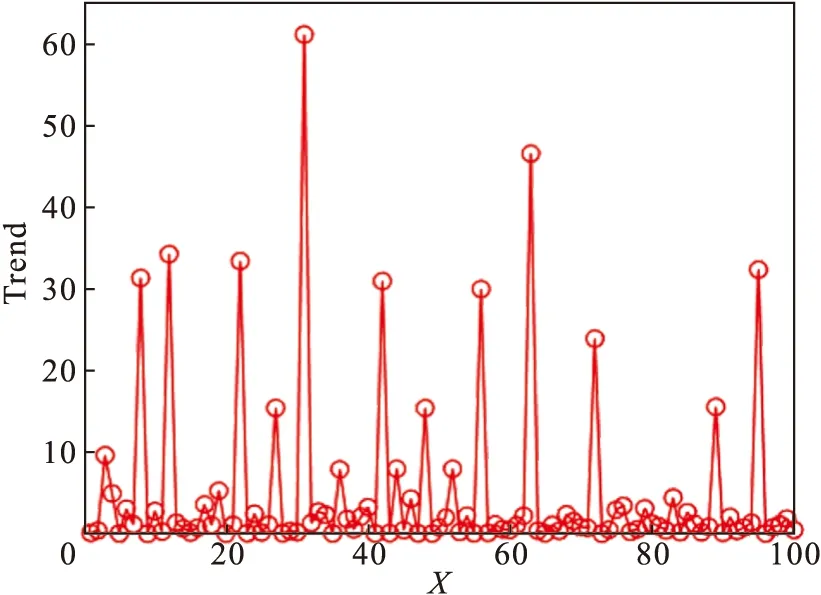
图6 下降趋势图Fig.6 The values distribution of Trend
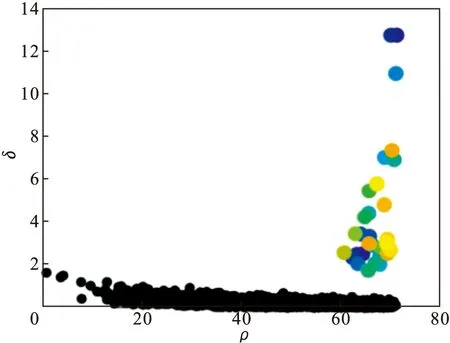
图7 聚类中心的选择Fig.7 Selection of cluster centers
5) 根据已选好的聚类中心和dc值进行聚类,最终聚类结果如图8所示,可以看出聚类效果较好.
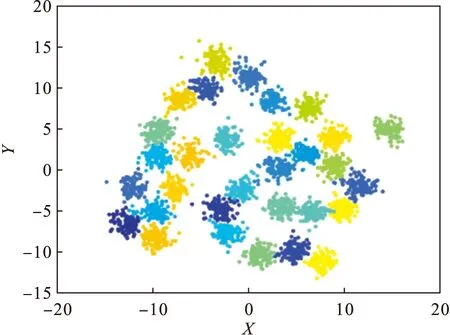
图8 聚类结果Fig.8 Clustering result
3.3 与DPC算法和K-means算法比较
3.3.1 聚类效果对比
本文将ADPC聚类算法与DPC算法和K-means算法进行了对比,D31,Data1,Data2,Aggregation,Spiral以及Fish数据集在3种聚类算法下的聚类结果如图9~图14所示.由聚类结果可以看出,Data1,Data2两种数据集下,3种算法具有差不多的效果,聚类均比较精确,但是在Aggregation、Spiral和Fish数据集下,3种算法的聚类效果差异较大.
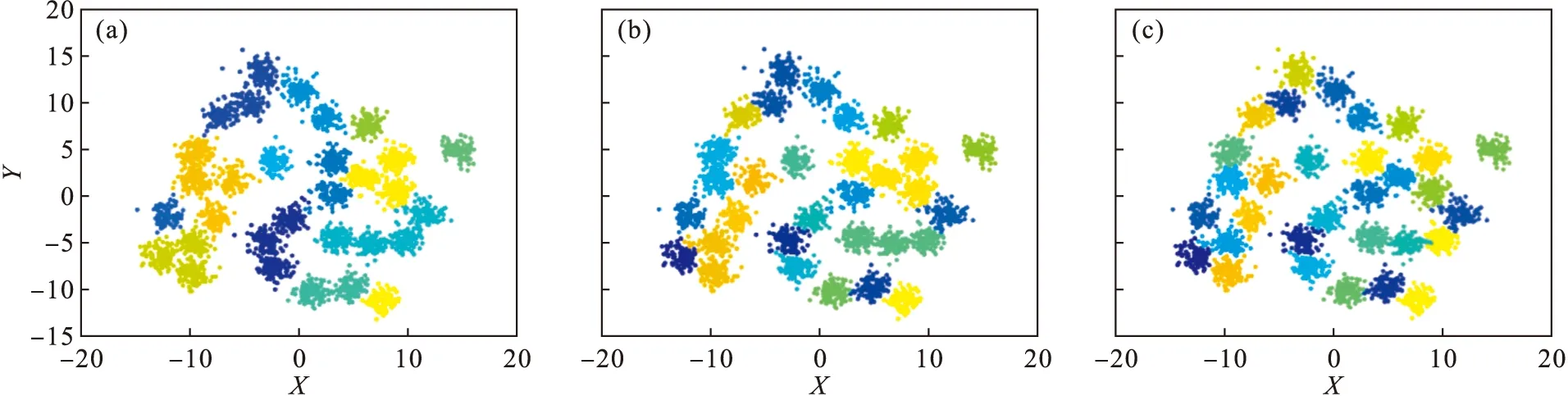
图9 D31数据集Fig.9 D31 data set(a)—DPC; (b)—K-means; (c)—ADPC.
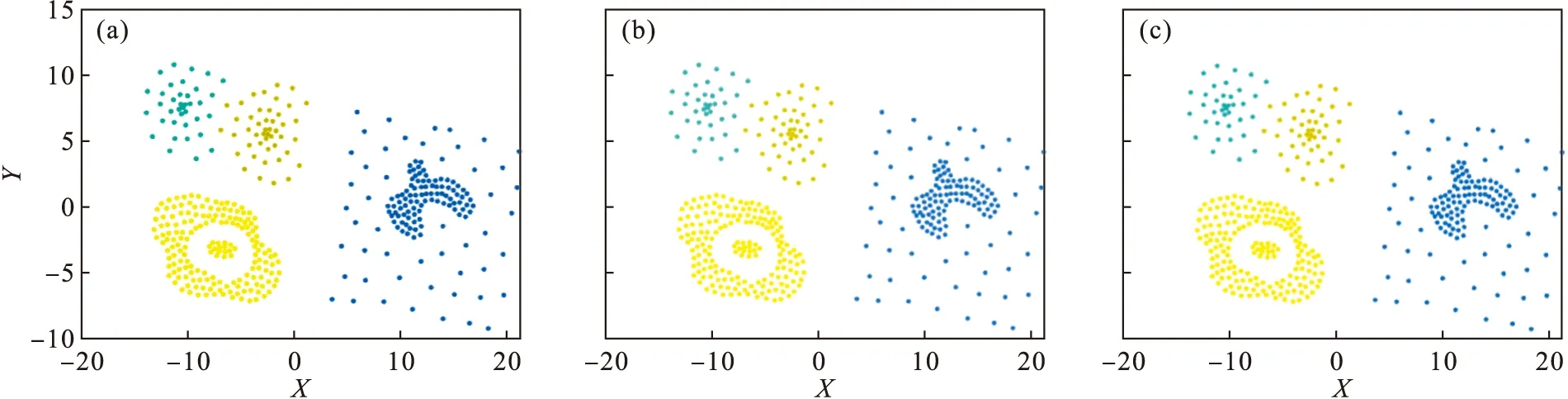
图10 Data1数据集Fig.10 Data1 data set(a)—DPC; (b)—K-means; (c)—ADPC.
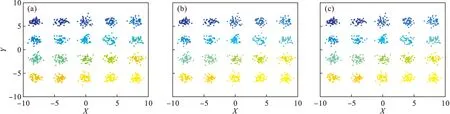
图11 Data2数据集Fig.11 Data2 data set(a)—DPC; (b)—K-means; (c)—ADPC.

图12 Aggregation数据集Fig.12 Aggregation data set(a)—DPC; (b)—K-means; (c)—ADPC.
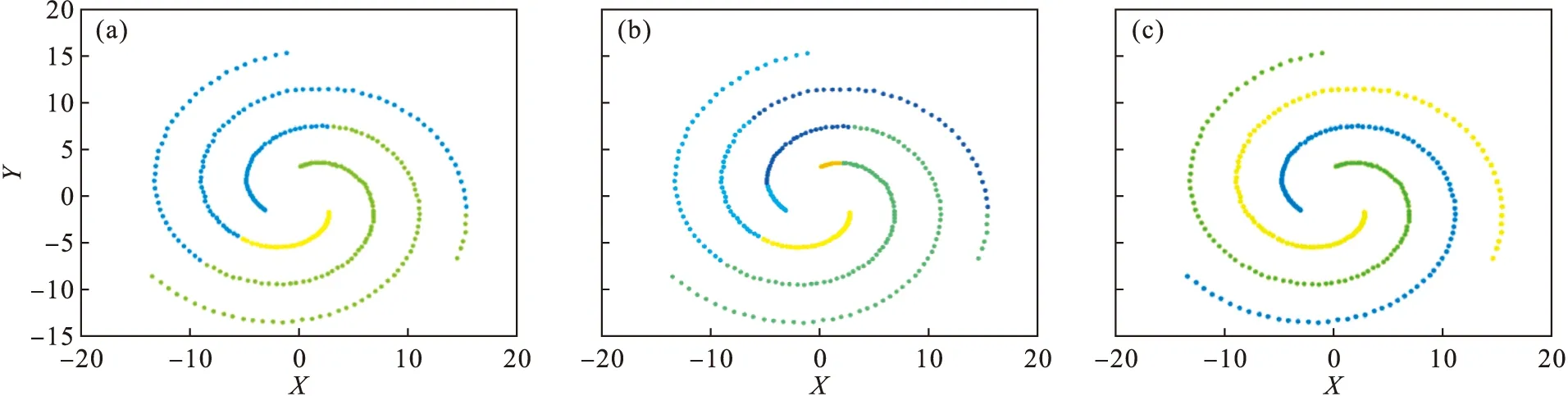
图13 Spiral数据集Fig.13 Spiral data set(a)—DPC; (b)—K-means; (c)—ADPC.
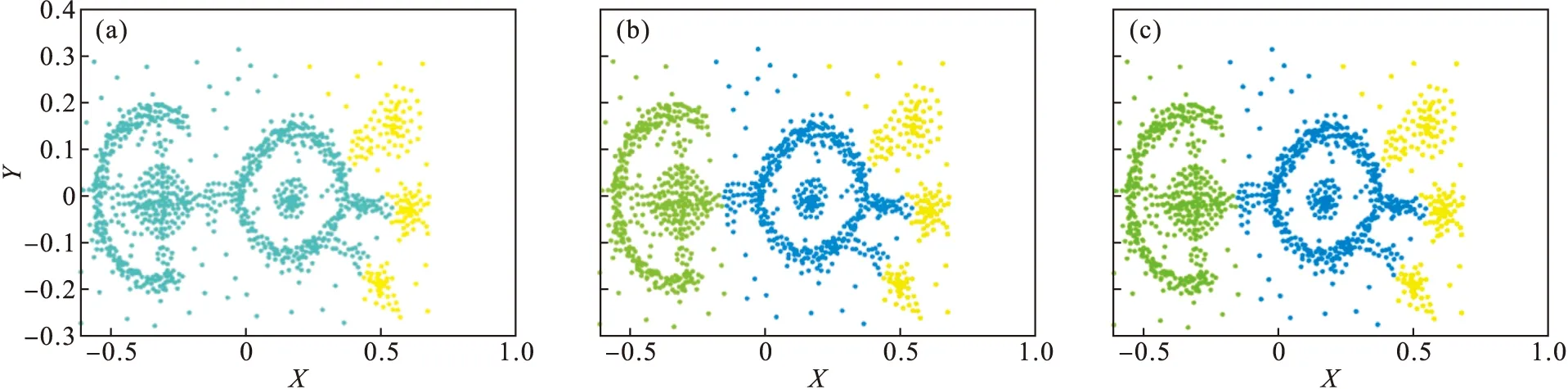
图14 Fish数据集Fig.14 Fish data set(a)—DPC; (b)—K-means; (c)—ADPC.
Aggregation数据集的聚类效果如图12所示,图12a为DPC算法的聚类效果,在DPC算法下的聚类类别的区分不够明显,左下角黄色的类别以及右侧黄色的类别没有得到划分.如图12b所示,K-means算法中左下角的两种类别被划分很精确,但是右侧的两种类别依然没有被划分开.ADPC算法的聚类效果见图12c,所有类别均被识别.
Spiral数据集在聚类数据集中比较具有代表性,与普通数据集不同的是,该数据集以环形分布,并且两种类别的聚类比较近,不具有明显的区别性.3种聚类算法的聚类效果见图13,可以看出图13a DPC算法和图13b K-means算法的聚类效果较差,图13c ADPC算法的聚类效果比较精确.
Fish数据集的聚类效果见图14,可以看出K-means算法和ADPC算法的聚类效果较好.
综上,针对一些容易区分的数据集,如Data1和Data2数据集,DPC,K-means和ADPC三种算法均有较好的聚类效果.但是对于一些不容易区分的数据集,如Aggregation,Spiral和Fish数据集,ADPC算法具有更好的聚类效果.
3.3.2 聚类效果评价
ARI指标的值在[-1,1]之间,值越大代表划分程度越高,说明聚类效果越好.DPC,K-means以及ADPC算法在6种数据集下的ARI值如图15所示.由图15可以看出,ADPC相比DPC和K-means算法具有更高的ARI值.
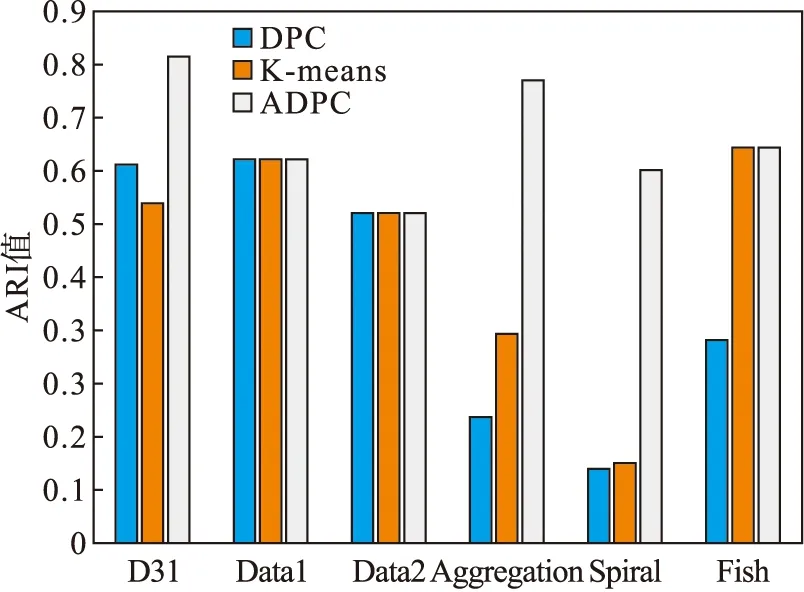
图15 ARI值对比Fig.15 Comparison of ARI values
NMI指标是度量两个类别相似程度的指标,在[0,1]之间取值,指标值越大代表聚类效果越好.DPC、K-means以及ADPC算法在6种数据集下的NMI值如图16所示,由图16可以看出,ADPC相比于DPC和K-means算法在绝大部分情况下具有更高的NMI值.
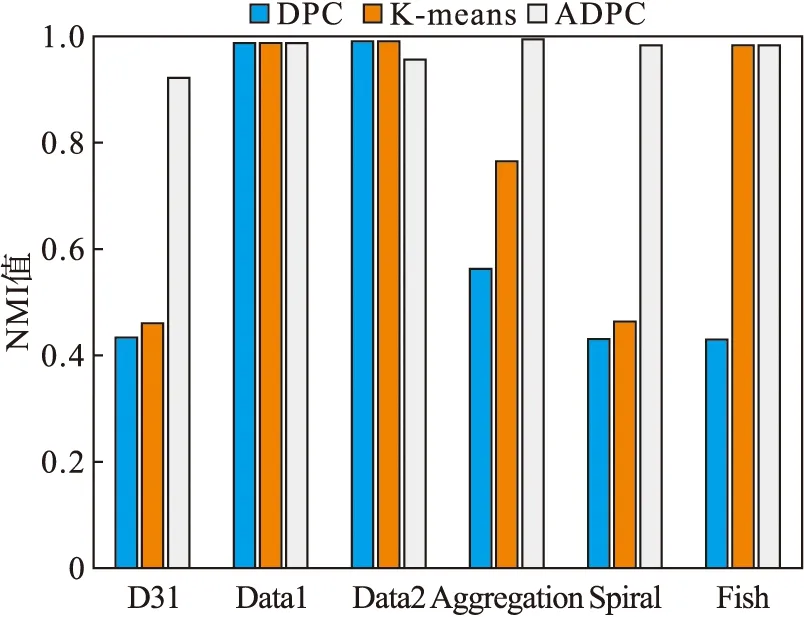
图16 NMI值对比Fig.16 Comparison of NMI values
AC指标是衡量聚类准确度的指标,在[0,1]之间取值,越接近1代表精确度越高.DPC、K-means以及ADPC算法在6种数据集下的AC值如图17所示,由图17可以看出,ADPC相比DPC和K-means算法具有更高的AC值.
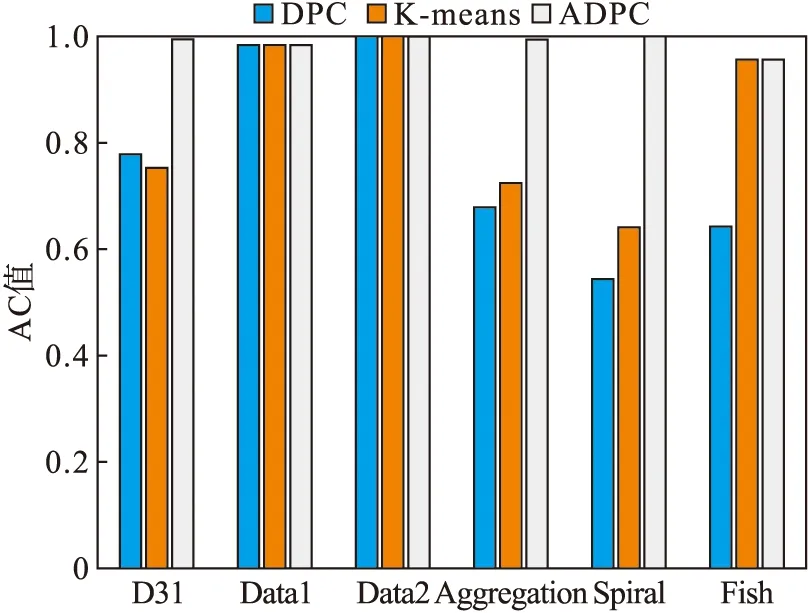
图17 AC值对比Fig.17 Comparison of AC values
综上,对ARI,NMI和AC三个指标的值进行整理,并计算平均值,如图18所示,结果显示,ADPC算法与DPC算法和K-means算法相比除了在Data2数据集中的NMI值低0.02以外,其他情况下均具有更高的ARI,NMI和AC值, 并且具有更高的ARI平均值、 NMI平均值和AC平均值.因此,ADPC算法具有相对于DPC算法和K-means算法更好的聚类效果.
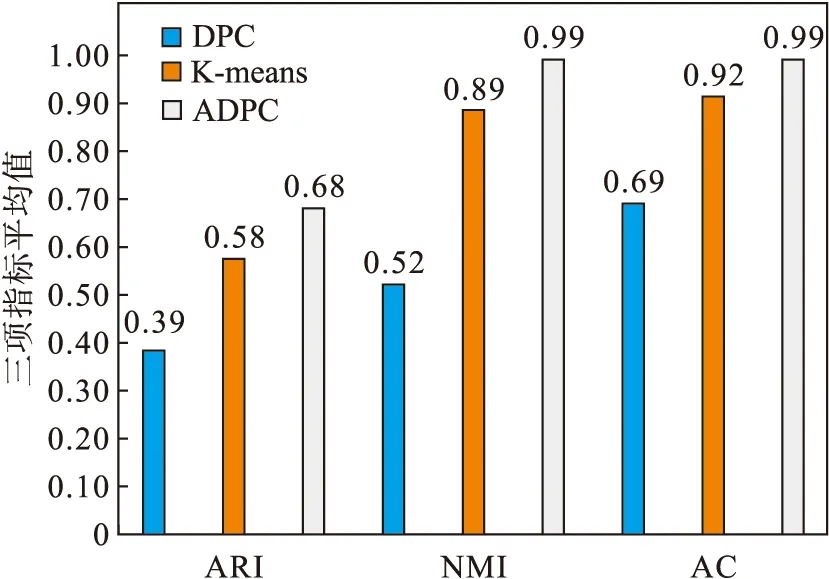
图18 三项指标的平均值Fig.18 Average of three indicators
4 结 语
本文对密度峰值聚类算法做出了改进,针对其不能自动选择聚类中心的缺点,重新定义了综合衡量局部密度ρi和δi相对距离的参量μi,针对其不能自动确定dc的问题,通过基尼系数去衡量dc的最佳值.选取了6组具有代表性的数据集进行了算法测试,首先根据D31数据集的聚类结果对自适应的聚类算法的聚类过程进行了详细介绍,最后将6组数据集的聚类效果与DPC聚类算法和K-means算法进行了对比,并分别分析了ARI,NMI和AC三个指标.结果表明,ADPC算法具有较好的聚类效果.
