基于改进迭代相邻互相关函数的高速高机动目标检测方法

王 阳，张小宽，马前阔，宗彬锋，郑舒予，徐嘉华

(1.空军工程大学防空反导学院，陕西 西安710051；2.国防科技大学ATR国防科技重点实验室，湖南 长沙 410073)

0 引言

随着航空航天技术的高速发展，现代飞行器普遍具有高速度、高机动的特征。目前，传统的预警雷达难以对此类高速高机动目标进行有效检测，导致国家空域安全面临严峻挑战[1-3]。

长时间相参积累技术[4-5]是解决这一问题的有效手段。但是，在相参积累过程中高速高机动目标会导致距离徙动和多普勒徙动现象的出现，严重影响动目标检测(moving target detection，MTD)算法性能[6-12]。因此，提高雷达对高速高机动目标的探测能力已成为当下雷达信号处理领域研究的热点。

目前，针对高速高机动目标检测出现的问题，典型的解决方法有基于Keystone变换(Keystone transform，KT)算法[13]、基于Radon傅里叶变换(Radon Fourier transform，RFT)算法[14-16]，它们能够在低信噪比的条件下有效校正一阶距离徙动，但这两类算法计算量较大，无法对加速度[17]、加加速度[18]造成的二阶、三阶距离徙动进行校正。针对具有加速度、加加速度的高速高机动目标，很多学者在KT变换和RFT变换的基础上提出了改进算法。如二阶Keystone变换(second-order Keystone transform，SKT)[19-20]、雷顿-分数阶傅里叶变换(Radon fractional Fourier transform，RFRFT)[21-22]、广义Radon-Fourier 变换(generalized Radon-Fourier transform，GRFT)算法[23-24]和基于相位差分与吕分布(phase differentiation and Lv’s distribution，PD-LVD)算法[25]等。上述这些算法能够有效校正，但是包含了参数搜索过程以及多次变换，运算量很大，较难用于雷达实时检测。

本文针对此问题提出基于改进迭代相邻互相关函数(adjacent cross correlation function，ACCF)算法的高速度高机动目标检测方法。该方法舍弃了传统方法所需的参数搜索过程，仅通过复乘、快速傅里叶变换(FFT)和快速傅里叶反变换(IFFT)就可快速地实现高速高机动目标的检测，并通过快速离散时间傅里叶变换(discrete time fourier transform，DTFT)实现运动参数估计。

1 目标回波信号模型

假设雷达发射信号为具有大时宽带宽积的线性调频(LFM)信号，则发射信号的表达形式为：

(1)

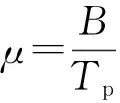
假设雷达探测单个运动目标，则运动目标与雷达的距离是随着tm变换的，忽略其他高阶分量，目标的距离R(tm)为：

(2)

式(2)中，R0为初始时刻目标与雷达之间的距离，ν为目标径向速度，a为目标径向加速度，g为目标径向加加速度。

雷达接收到目标的基带回波信号可表示为：

(3)

式(3)中，σ为目标的反射率，c为电磁波在空气中的传播速度。脉冲压缩以基带发射信号时间反褶后的复共轭为参考信号。

(4)

(5)

通过式(3)和式(5)可以看出，脉压后回波信号峰值和相位都和目标运动参数有关。高速高机动目标会使回波信号能量在积累时间内分布在不同距离单元，同时回波信号相位是关于tm的三阶函数，将会导致出现距离徙动和多普勒徙动现象，给雷达检测目标带来很大困难。

2 改进迭代ACCF算法

2.1 迭代ACCF原理

只考虑单个目标脉冲压缩后的回波信号，即

(6)

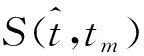
(7)

式(7)中，*表示对信号取共轭。两个信号的时域求和与频域响应乘积的逆傅里叶变换乘等效，即

r1(τ1，tm)=IFFT[S(f，tm)S*(f，tm+1)]，

(8)

式(7)中，

(9)

(10)

把式(9)和式(10)代入式(8)，得

(11)

式(11)中，A3为r1(τ1，tm)的幅度，

(12)

(13)

(14)

(15)

如式(11)所示，多普勒徙动被消除，信号峰值落在

(16)

(17)

(18)

式中，fr为脉冲重复频率，fs为采样频率。如果满足式(17)和式(18)的条件，式(16)的峰值位置便会落于同一位置单元。因此，通过ACCF算法可以同时校正距离徙动和多普勒徙动。

对比式(6)和式(11)可以看出，回波的距离徙动和多普勒徙动阶数都从3阶变为2阶，说明ACCF算法对回波具有降阶作用。对第一次ACCF运算的结果再进行ACCF运算，可以再一次对回波进行降阶。一般称两次及以上的ACCF运算为迭代ACCF算法。

对r1(τ1，tm)再进行一次ACCF运算，可得第二次ACCF变换的结果：

(19)

式(19)中，A4为第二次ACCF运算后信号的幅度

(20)

M2=2N4Tr。

(21)

易知M1和M2的数值比较小，因此目标的距离单元可确定在τ2=0或相邻单元处，此时沿着tm的方向做FFT即可完成对回波的相参积累，积累后的结果如下：

(22)

2.2 快速DTFT算法

在迭代ACCF算法估计目标运动参数时，通常用FFT来实现。目标运动参数的估计精度与FFT点数有关，当对参数精度有要求时，需要对FFT运算进行大量的补零，这不仅造成了频带浪费，而且增加了运算量。针对此问题，本文采用快速DTFT对部分频谱细化分析[26]来进行运动参数估计。

对于离散信号，常规DTFT定义为：

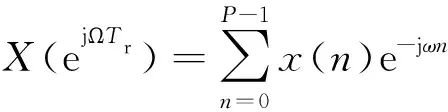
(23)

对部分频谱进行细化分析时，根据估计精度确定频谱的基本范围(fmin，fmax)、频率分辨率f0和计算点数R，代入式(23)得

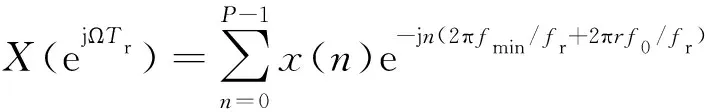
(24)

式(24)中，r=0，1，2，…，R-1。

快速DTFT算法通过布鲁斯坦提出的式(25)来设计，

(25)

则式(24)可以变形为：

(26)

式(26)中，g(n)=x(n)e-j2πn(fmin+0.5nf0)/fr，h(n)=ejn2πf0/fr。

通过式(26)可以看出，计算R点DTFT只需计算序列g(n)与h(n)的卷积以及e-jr2πf0/fr的乘积。在计算卷积时，可以用FFT来实现，选取的FFT点数要满足L≥N+R-1，且L是2的整数次幂。在快速DTFT计算过程中，计算g(n)需要2P次复乘，计算循环卷积需要L次复乘，计算3次FFT需要1.5LlbL次复乘，与e-jr2πf0/fr相乘需要R次复乘。综上，快速DTFT算法复乘运算量为1.5LlbL+L+2P+R。

2.3 改进算法运动参数估计过程

使用快速DTFT算法实现目标运动参数估计过程如下。

步骤1 对目标回波信号进行迭代ACCF运算，分别得到第一次运算的结果r1(τ1，tm)、r1(τ1，ftm)和第二次运算的结果r2(τ2，tm)、r2(τ2，ftm)；

步骤2 估计高速目标加加速度的大致范围，确定需要细化分析的频谱范围(fmin，fmax)，根据估计精度确定快速DTFT的点数，通过对r2(τ2，tm)沿tm方向进行DTFT运算得到加加速度g的估计值；

步骤3 根据加加速度的估计值得到参考函数并与r1(τ1，tm)相乘，估计高速目标加速度的大致范围，确定需要细化分析的频谱范围 ，根据估计精度确定快速DTFT的点数，通过对r1(τ1，tm)沿tm方向进行DTFT运算得到加速度a的估计值；

步骤4 根据加速度和加加速度的估计值得到参考函数并与r1(τ1，ftm)相乘，估计高速目标速度v的大致范围，确定需要细化分析的频谱范围 ，根据估计精度确定逆DTFT的点数，通过对r1(τ1，ftm)先沿ftm方向进行逆DTFT，再沿tm进行FFT，得到速度的估计值。

本文的改进算法具体实现流程如图1所示。

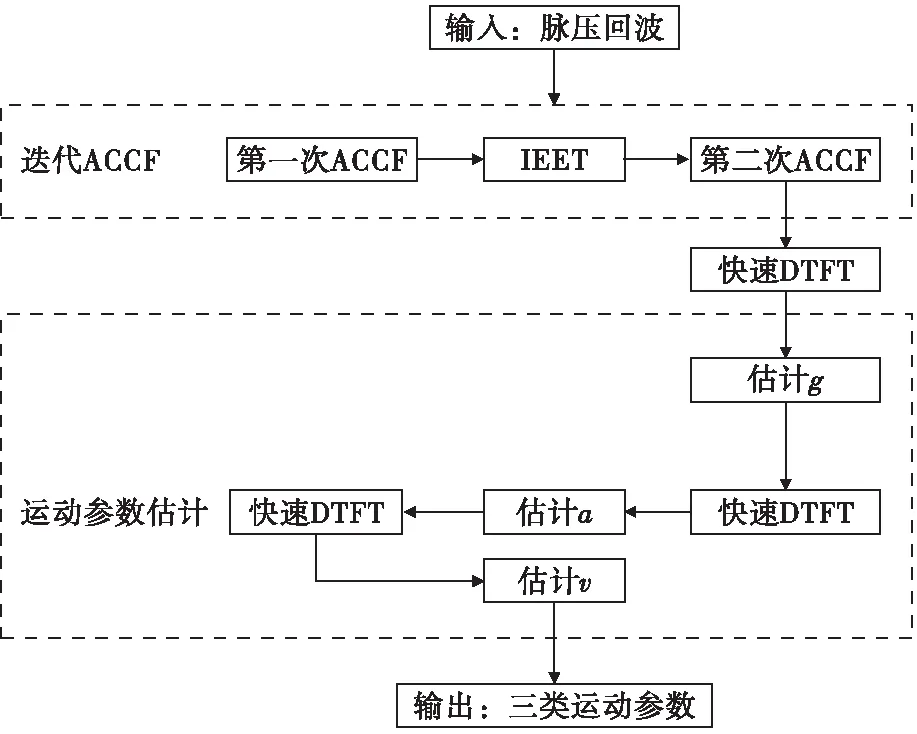
图1 改进算法流程图Fig.1 Flow chart of the improved algorithm

3 仿真实验

3.1 改进迭代ACCF算法仿真分析

通过仿真实验验证改进迭代ACCF算法的性能，设有效脉冲数为512，目标速度为800 m/s，加速度为100 m/s2，加加速度为50 m/s3。

设定雷达系统参数：载频为1 GHz，带宽为 9 MHz，脉冲宽度为10 μs，脉冲重复频率为200 Hz，采样率为36 MHz。分别设定信噪比为-5 dB和5 dB两种情况，仿真结果如图2、图3所示。

从图2(a)、图3(a)可以看出，使用传统方法对目标进行检测会出现距离徙动和多普勒徙动现象；根据图2(b)、图3(b)、图2(c)、图3(c)可得，通过改进迭代ACCF算法处理之后，信号回波能量集中在同一距离单元，有效校正了距离徙动和多普勒徙动现象；从图2(d)、图3(d)中可以观察到目标能量经过积累后形成了明显的峰值，有利于后续的目标检测与运动参数估计。通过比较两种不同信噪比的仿真实验结果，可以发现在低信噪比条件下，改进ACCF算法聚焦效果会变得模糊。因此可知改进ACCF算法对噪声比较敏感，而如何有效地提高检测信噪比，改善算法在低信噪比条件下的参数估计性能，是后续的重要研究方向。

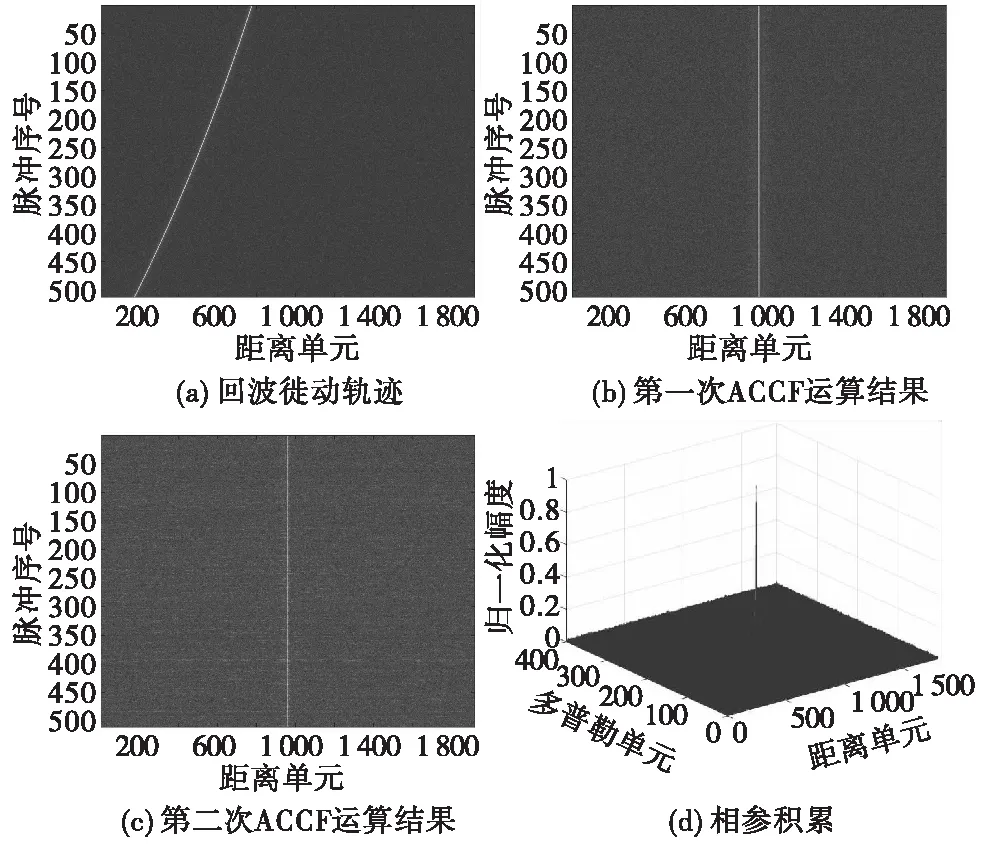
图2 信噪比为-5 dB条件下，改进算法的检测结果Fig.2 Detection results of improved algorithm at SNR=-5 dB

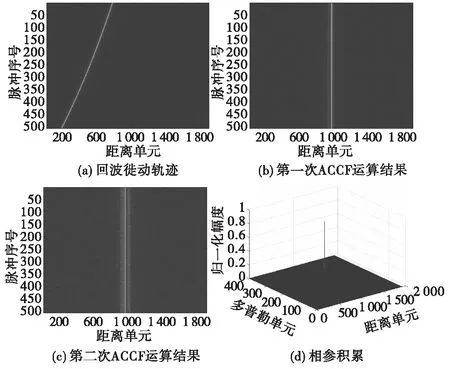
图3 信噪比为5 dB条件下，改进算法的检测结果Fig.3 Detection results of improved algorithm at SNR=5 dB

3.2 运算复杂度比较

设置目标运动参数估计精度范围为：0.1～1，对改进算法与传统算法的运算复杂度进行比较，仿真结果如图4所示。

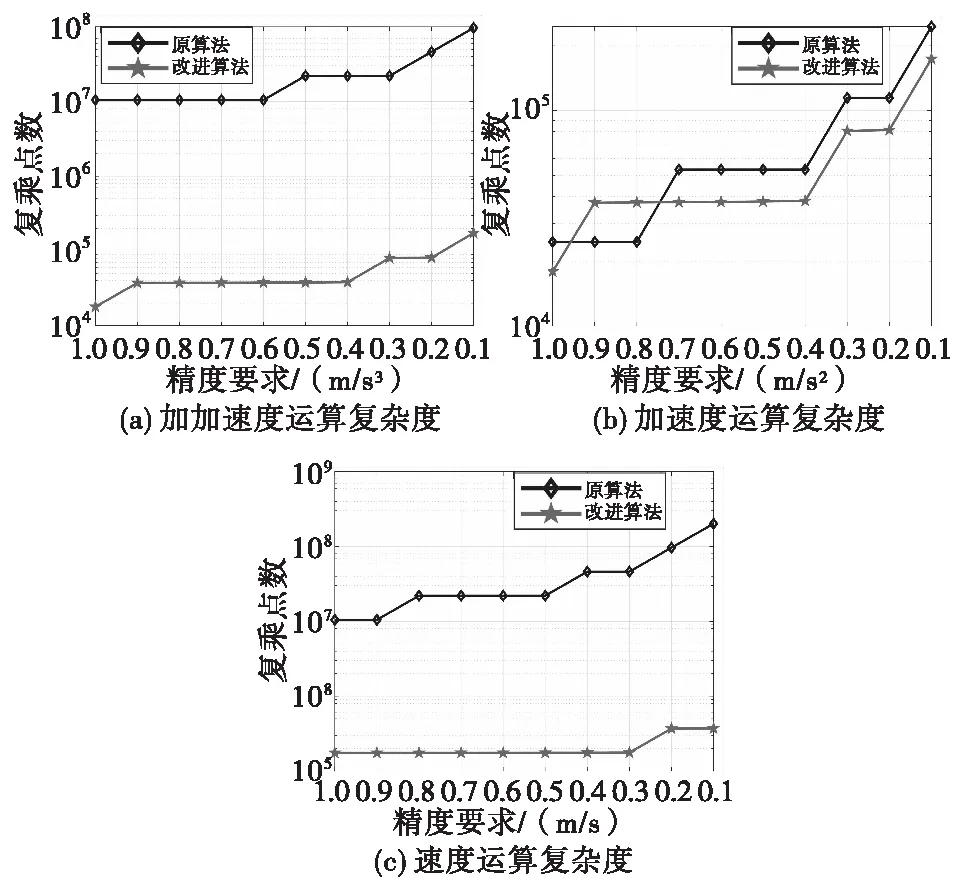
图4 改进算法与传统算法运算复杂度比较Fig.4 Computational complexity comparison of the improved algorithm and the traditional algorithm

从图4(a)、图4(c)中可以明显看出本文改进算法的运算复杂度低于原算法。在图4(b)中，在估计精度要求不高的情况下原算法的复杂度要低于本文改进算法，这是因为快速DTFT与FFT运算在估计参数时都需要进行补零，在估计加速度时补零较少，而快速DTFT要对频谱进行细化分析，复杂度较高；但在参数估计精度要求较高时，本文改进算法复杂度较低。因此，与传统的ACCF算法相比，本文所提出的改进算法在参数估计精度较高的条件下，运算复杂度更低、运算速度更快，可实现高速高机动目标的快速检测。

3.3 运动参数均方差分析

设置信噪比范围为-20～10 dB。在不同信噪比条件下，改进迭代ACCF算法的运动参数估计均方差(RMSE)如图5所示。

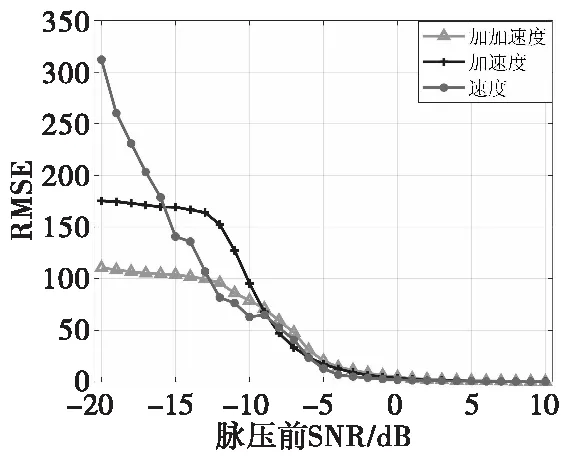
图5 改进迭代ACCF运动参数均方差Fig.5 RMSE of improved iterative ACCF motion parameters

从图5中可以看出，当信噪比低于-5 dB时，运动参数的均方差差距较大，对加加速度的估计精度明显优于加速度和速度的估计。分析原因可知：在参数估计过程中，加速度和速度的估计要依赖于加加速度的估计。当信噪比高于-5 dB时，各类运动参数估计的误差均接近于0，因此可以验证：在较高的信噪比条件下，改进算法可有效实现对不同运动参数的准确快速估计。

4 结论

本文提出改进的迭代ACCF算法来实现高速高机动目标的快速有效检测。相较于传统的迭代ACCF算法，该算法通过快速DTFT实现目标的参数估计，能够进一步降低算法复杂度。仿真实验结果表明，本文算法在较高信噪比条件下能够快速有效的校正距离徙动和多普勒徙动，且在保证参数估计精度的情况下降低了算法复杂度，对高速运动目标的快速检测跟踪具有重要意义。