基于小波变换的边缘检测技术

刘光宇 刘 彪 曾志勇 赵恩铭 邢传玺

(1. 大理大学 工程学院， 云南 大理 671003；2. 哈尔滨工程大学 物理与光电工程学院， 哈尔滨 150001；3. 云南民族大学 电气信息工程学院， 昆明 650031)

0 前 言

边缘检测是图像处理的关键技术，在图像分割、识别等领域有着重要的应用[1-2]。边缘检测一般包括图像滤波、图像增强、图像检测以及图像定位等 4个步骤[3]。传统的图像边缘检测方法有2种：一种是基于查找的一阶微分算子，包括Sobel算子[4]、Roberts算子、Prewitt算子等；另一种是基于零穿越的方法，该方法是寻找图像像素点二阶导数的零交叉点，并采用平滑滤波，降低噪声的影响。但是，采用这些算子提取的图像效果并不理想。文献[5]中，Roberts算子对复杂边缘信息提取不全。文献[6]中，Canny算子具有很好的信噪比，图像定位更加准确，但提取的图像存在部分虚假边缘，在具体应用上，具有一定的局限性。文献[7]中，由传统小波变换得到的边缘定位不良，图像容易产生伪边缘。文献[8]中，传统Sobel算子结构简单，但其并没有对图像的主体与背景进行严格区分。针对以上问题，考虑在小波变换的基础上，采用 Roberts算子对图像的边缘信息进行提取。

1 Roberts算子

Roberts算子是利用局部差分，寻找边缘的梯度算法[9]。首先，对每一个梯度的像素值进行计算；然后，依次求取每个梯度的绝对值；最后，在一定阈值下，进行梯度运算的综合操作。Roberts算子常用来处理低噪声图像，当图像边缘接近+45°或-45°时，该算子的处理效果更理想。

Roberts算子公式如式(1)所示：

(1)

式中：g(x,y)表示梯度幅值的近似值；f(x,y)表示坐标点(x,y)处的二维信号。

通过差分运算,计算g(x,y)，并设定合理的阈值Th。若g(x,y)>Th,说明该点为阶跃状边缘点[3]；反之，则说明该点不是边缘点。Roberts算子的物理聚焦效果较好，但没有对图像进行均值化处理，因此不适用于提取具有陡峭边缘的图像。

2 小波变换方法

图像边缘是指特定区域灰度值发生突变的地方。小波变换具有良好的局部特性和多分辨率分析等特点，能实际多尺度逼近边缘，因此适用于边缘检测[5]。通过小波变换的模极大值点，可以判断图像边缘的具体位置。

2.1 二维小波变换

图像存在于x轴和y轴的交叉区域，其中每个像素点都有其对应的坐标点，每个坐标点的时域，显示为一个连续的二维信号。小波变换一般采用二维离散的方法，即对二维图像信号在水平和垂直方向，进行一维离散小波变换。

二维连续小波公式如式(2)所示[10]：

(2)

式中：ψ(x1,y1)表示二维基本小波；ψa;x2,y2(x1,y1)表示ψ(x1,y1)的尺度伸缩和二维位移;a表示伸缩因子；b表示位移因子;x2、y2表示发生位移后的坐标。

对二维连续小波进行小波变换，如式(3)所示：

WTf(a;x2,y2)=

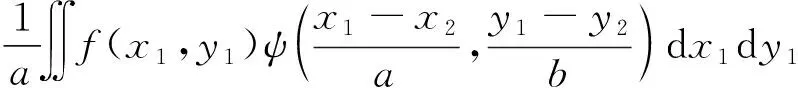
(3)

式中：f(x1，y1)表示坐标点(x1,y1)的二维信号，f(x1,x2)∈L2(R2)。

与一维小波相比，二维小波操作相对复杂，需要对其进行尺度收缩和坐标旋转，如式(4) — 式(5)所示：

A=crθ

(4)

(5)

式中：c表示尺度因子；rθ表示旋转因子。

二维小波的变换方程如式(6)所示：

(6)

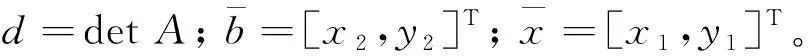
2.2 Mallat算法

Mallat算法的原理是，通过信号f(x,y)，将尺度J转换到Vj和Wj，得到离散逼近值ajf、djf。其中，Vj和Wj为存在于L2(R)的两个相交空间。分解尺度设置为J+1，将ajf分解到对应的子空间Vj+1和Wj+1上，按照上述方法依次迭代，从而实现多分辨率的分解。信号f(x,y)的多尺度分解过程，如图1所示。

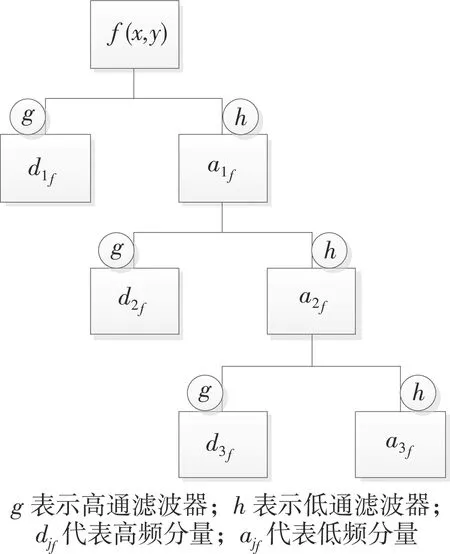
图1 信号f(x,y)的多尺度分解过程

二维离散小波变换Mallat分解，如式(7) — 式(8)所示：

(7)

(8)

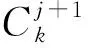
将式(7)和式(8)代入小波函数，得到Mallat的塔式算法，如式(9)所示：

(9)

2.3 小波模极大值计算

对于任意图像像素点p(x,y)，小波变换在水平和垂直方向得到的小波系数都是独立的，可以利用向量原理计算它的模和幅角[11]。

设θ(x,y)为二维光滑函数，满足式(10)：

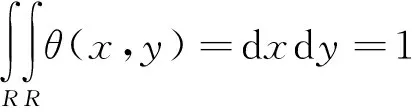
(10)

求取θ(x,y)在x,y方向的一阶导数，得到2个基本小波，如式(11)所示：

(11)

其相应的二维小波变换，如式(12)所示：

(12)

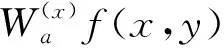
小波变换模定义，如式(13)所示：

(13)

将梯度的模转化为梯度相角，可得到式(14)：

(14)

采用Mallat算法，得到梯度矢量，梯度矢量方向即为梯度模局部极大值的方向。沿着梯度矢量方向检测小波变换系数模的局部极大值点，即可得到图像的边缘点[12]。

3 小波变换边缘检测算法的实现

利用小波变换的边缘检测算法，对图像进行边缘检测，具体操作如下(见图2)：

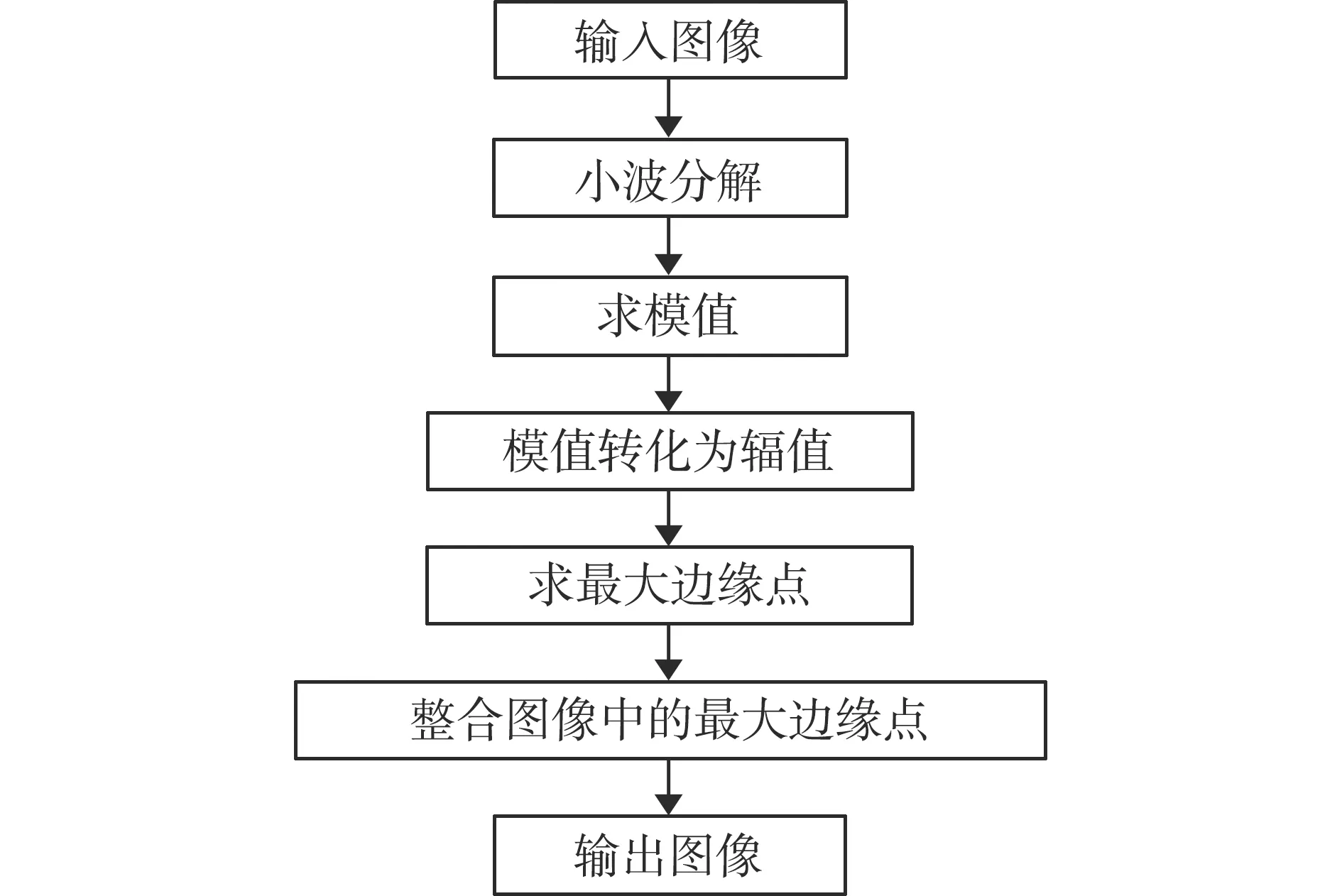
图2 基于小波变换的图像边缘检测步骤

(1) 输入图像。

(2) 对图像进行小波分解。

(3) 求取小波变换系数的模值。如式(15)所示:

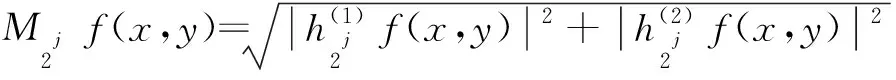
(15)

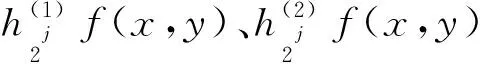
(4) 模值转化为辐值。对幅角进行4等分(见图3)，计算0°、45°、90°、135°等方向的偏导数、水平和垂直方法的差方，计算特殊区域的模值，并将其转换为幅值。

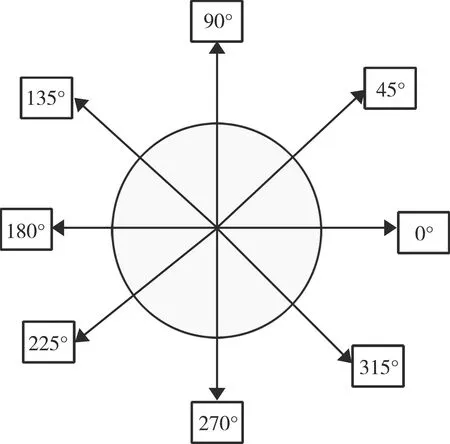
图3 幅度划分图

(5) 求最大边缘点。按前面各方向依次对每一个像素点进行检测。如果检测到极大值点，保留并记录为边缘点；否则，梯度值设为0。

(6) 整合图像中的最大边缘点。利用小波变换尺度的多样性，对图像中的边缘点进行融合。

(7) 输出图像。

4 仿真实验和结果分析

4.1 边缘图像的对比

选取一张像素为512×512的瓷砖图像，对其进行灰度值计算，结果如图4所示。

图4 图像对比

设置分解尺度J=1，采用低通、高通滤波器对图4进行卷积和偏导，生成第一级小波分解图像，如图5所示。第一级小波分解提取的图像边缘轮廓信息较少，无法分辨出所有地砖的模型，只能分辨出明显的突变点，并且图像背景中包含许多虚假信息。

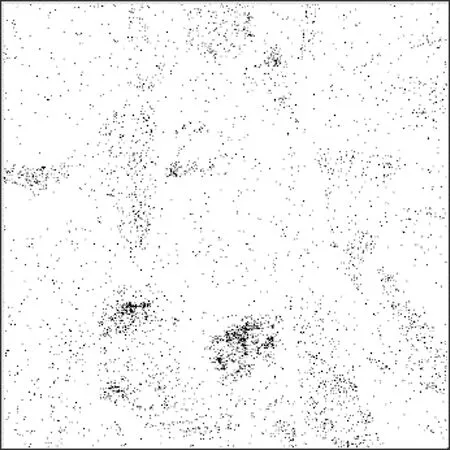
图5 第一级小波分解的图像边缘

设置分解尺度J=2，更新低通、高通滤波器，进行卷积和偏导，生成第二级小波分解，结果如图6所示。与第一级分解相比，第二级小波分解得到的图像拥有更多的边缘细节，但图像边缘仍然比较模糊。

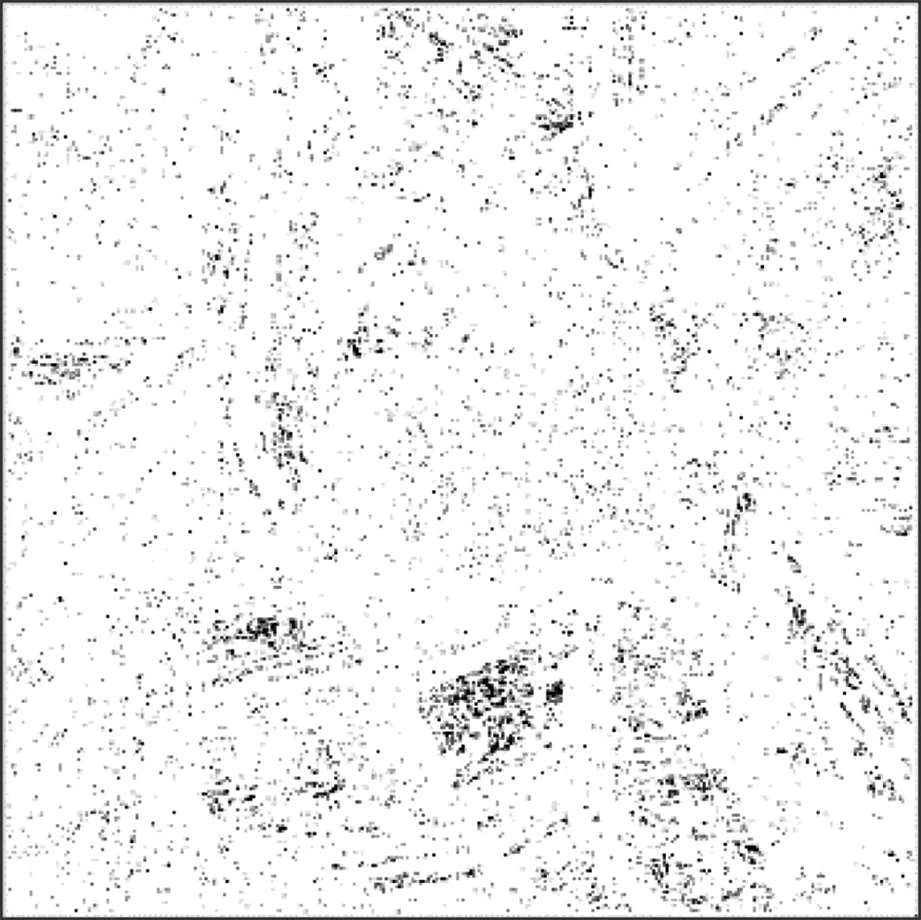
图6 第二级小波分解的图像边缘

选取绝对值相对大的小波系数，对分解的小波图像进行融合，其处理区域为3×3。首先，求取图像中模的极大值，并转换为幅值，寻找各方向最大值点，并将其设置为边缘点；然后，连接图像所有的边缘点，形成图像边缘(见图7a)。在Matlab中，调取Roberts函数，对图4进行边缘提取(见图7b)。

图7 不同方法提取的图像边缘

由图7可知，与传统Roberts算子相比，经过小波处理后得到的图像边缘，拥有更多的细节信息。采用传统Roberts算子提取的图像，地砖样貌缺少一些重要的边缘信息；采用本次研究方法提取的图像边缘几乎连续，能够得到较为清晰的地砖轮廓和纹理，定位更加精确，检测到的边缘信息更加完整。

4.2 边缘提取评价

采用Dice(Dice Coefficient)系数和召回率(Recall)等指标，对图像边缘提取效果进行评价。

Dice系数是一种集合相似度度量函数，通常用于计算两个样本的相似度,计算结果的范围为[0，1]。其计算如式(16)所示:

(16)

式中：|X∩Y|表示集合X与集合Y的交集； |X|和|Y|分别表示元素个数。

分别采用本文次研究的方法和传统Roberts算子，对图像边缘信息进行提取，得到的图像相似度对比，如图8所示。对图像边缘提取效果进行评价，结果如表1所示。表中召回率为判定正确的数据所占比重。

图8 图像边缘提取相似度对比

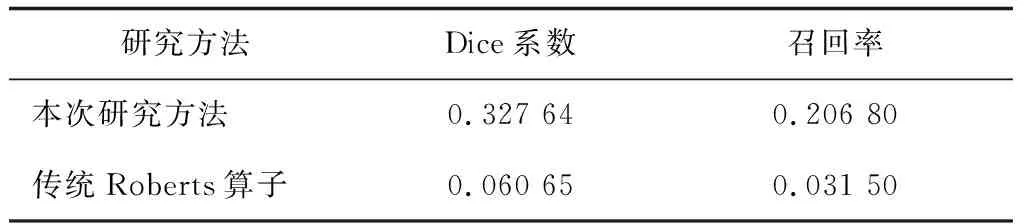
表1 图像边缘提取效果评价

图8中，白色线条为提取的图像与理想图像重合相似的地方，绿色是除去瓷砖之外的纹理点。由图可知，采用本次研究的方法提取的图像边缘，与理想边缘图像更加相似。

由表1可知，传统Roberts算子与本次研究的方法的Dice系数相差5倍左右，召回率相差6倍左右。采用本次研究方法对图像边缘进行提取，效果更好。

5 结 语

本次研究在小波变换基础上，采用Roberts算子对图像边缘进行检测。首先，对图像进行小波分解，利用Roberts算子求各方向的模极大值，从而确定图像的真实边缘；然后，对图像进行融合，得到边缘检测图。研究结果显示，采用本次研究方法对图像边缘进行提取，可获得更多的纹理信息，边缘细节更突出，边缘定位的精确度更高。