求解L1正则化L2损失支持向量机问题的多层随机坐标下降算法

徐宇淼， 徐文静， 胡清洁

(桂林电子科技大学 数学与计算科学学院，广西 桂林 541004)

支持向量机(SVM)是Vapnik等[1-2]根据统计学习理论中结构风险最小化原则提出的，也是借助最优化方法解决机器学习和数据挖掘中若干问题的有力工具。SVM的主要思想是建立一个最优的决策超平面，使这个超平面的两侧距离该平面最近的两类样本之间的距离最大化，从而为分类问题提供良好的泛化性能。SVM拥有坚实的理论基础和通用性、鲁棒性、计算简单等优点[3]，能有效解决小样本、非线性、过学习、局部极值等一系列难题，使其受到广泛关注。SVM已成功应用于文本分类[4]、信号识别[5]、混沌时间序列预测[6]、医学图像处理[7]、遥感图像分析[8]、干旱预测[9]、人脸识别[10]等领域。本研究考虑L1正则化线性分类的L2损失SVM问题。

L1正则化线性分类的L2损失SVM问题模型为

(1)

其中，

为平均L2损失函数。g(x)=λ‖x‖1是L1正则化函数，λ>0。L1正则化线性分类的L2损失SVM问题的输入数据是一个训练数据点集(aj,yj)∈Rn×{-1,1},j=1,2,…,N，其中aj为特征向量，yj为aj对应的标签，N>0。问题(1)中的L1正则项可以保证解的稀疏性，因此成为近年来的一个研究热点。目前求解L1正则化L2损失SVM问题的算法有很多，如坐标梯度下降法[11]、一维牛顿方向的坐标下降法(CDN)[12]、信赖域牛顿算法(TRON)[12]、随机块坐标下降法[13]、对偶坐标下降法[14]、牛顿型法[15]、邻近梯度法[16]、加速邻近梯度法[17]等。2007年，Tseng等[11]用坐标梯度下降法求解L1正则化问题，建立了该方法的全局收敛性，且在局部Lipschitz误差界假设下，该方法具有线性收敛性。2008年，Chang等[18]采用一维牛顿方向的坐标下降法(CDN)来求解线性L2正则化L2损失SVM问题。该算法在固定其它变量的同时，使一个单变量子问题最小化，子问题采用线搜索的牛顿步求解。该算法以线性速度全局收敛。实验结果表明，该算法比文献[19-20]算法更高效、更稳定。2010年，Yuan等[12]对L1正则化线性分类问题进行了研究，通过扩展CDN算法[18]和TRON算法[20]求解L1正则化L2损失SVM问题，且求解子问题时均使用广义的Hessian矩阵，并利用二阶信息。此外，文献[12]利用文献[21]中的束方法求解L1正则化L2损失SVM问题，数值实验结果表明，CDN算法训练数据集的时间最短，TRON算法训练数据集的时间优于束方法。2012年，Yuan等[15]提出牛顿型法求解L1正则化逻辑回归问题和L1正则化L2损失SVM问题，数值实验结果表明，求解L1正则化逻辑回归问题时，牛顿型法比CDN算法有效，求解L1正则化L2损失SVM问题时，CDN算法比牛顿型法更有效。2014年，Richtrik等[13]提出求解复合凸优化问题的随机块坐标下降法。该算法对求解大规模的L1正则化L2损失SVM问题是有效的。

鉴于此，针对问题(1)，基于多层优化思想[22-23]和随机坐标下降算法[13]，提出一种求解问题(1)的多层随机坐标下降算法。当迭代点满足粗糙条件时，该算法将求得粗糙模型的解用于计算精细模型的搜索方向，然后利用Armijo线搜索求解步长，从而得到下一个迭代点，否则，利用随机坐标下降算法求解精细模型的下一个迭代点。数值实验结果表明，该算法求解L1正则化L2损失支持向量机问题是有效的。

1 多层随机坐标下降算法

对L>0，F(x)在点x处的复合二次近似为

其中，

其极小点为

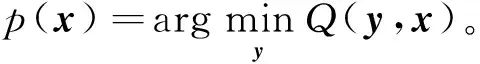
为保证算法的收敛性，选取的限制算子R和延拓P需满足条件σP=RT，其中σ>0，σ=1。根据文献[24]，选取限制算子R和延拓算子P，其中，

R=

求解问题(1)的多层随机坐标下降算法如下。

算法1多层随机坐标下降算法(MRCDA)

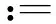
2)若不满足粗糙条件

(2)

则转步骤3)，否则，执行NH次粗糙迭代，得到xH,NH，计算

dk(xk)=P(xH,NH-Rxk),

其中，H表示多层优化方法中的粗糙层。由Armijo线搜索求得步长sk，即满足

Fμ(xk+skdk)≤Fμ(xk)+cskFμ(xk)Tdk。

令

xk+1=xk+skdk，

转步骤4)。

3)计算xk+1。对于i=1,2,…,l，随机选择j∈{1,2,…,n}，令p(x)=xk，计算

令

xk+1=p(x)+t*ej。

4)计算相对误差：

若er<ε，则停止计算，输出xk+1，否则，转步骤2)。

2 算法分析

多层优化方法的主要思想是，当迭代点满足粗糙条件(2)时，构造一个粗糙模型，将粗糙模型求得的解用于计算精细模型的搜索方向。

多层优化方法的目标是找到精细模型的最优解，粗糙模型仅作为辅助模型来构造搜索方向。设问题(1)的精细模型为

Fh(xh)=fh(xh)+λ‖xh‖1，

其中，

h为多层优化方法中的精细层。

由于光滑问题比用次梯度法求解原问题更有效，求解非光滑最小化问题时，可用一系列光滑问题替代原问题[22]。为此，引入一个光滑参数μ>0，对g(x)进行光滑化，得到gμ(x)。光滑后的目标函数为

Fμ(x)=f(x)+gμ(x)，

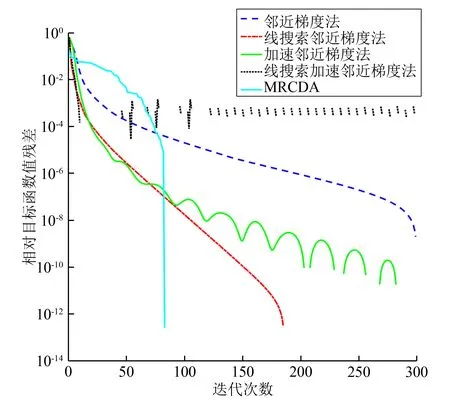
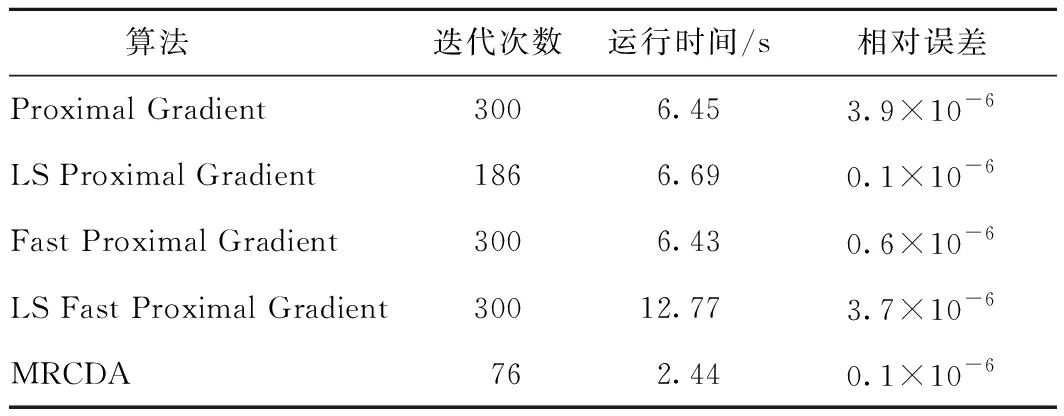
多层优化方法首先需要在层次之间传递信息，分别引入线性限制算子R∶RnH×n和延拓算子P∶Rn×nH，其中nH

dk(xk)=P(xH,NH-Rxk)。

其次需要构造粗糙模型。构造粗糙模型的关键是保证在初始点xH,0处粗糙模型与精细模型的最优性条件相匹配，可通过在粗糙模型的目标函数中添加一个线性项得到粗糙模型的目标函数：

FH(xH)=fH(xH)+gH(xH)+〈vH,xH〉，

(3)

其中，

vH=RFμ(x)-(fH(Rx)+gH(Rx))。

若当前迭代点xk满足粗糙条件(2)，则执行步骤2)。此时，为满足相容性FH(Rx)=RFμ(x)，用xH,0=Rxk开始粗糙迭代，利用一阶方法求解粗糙模型(3)，得到xH,NH，然后构造搜索方向dk(xk)=P(xH,NH-Rxk)，其中，xH,NH∈RnH为执行NH次迭代后粗糙模型的近似解。但在实际问题中，一般不易找到精确解，而是执行算法NH次迭代后，直到找到一个可接受的近似解xH,NH。此外，利用Armijo线搜索求得步长sk，即找到最小的k，使得sk=τk-1s0满足

Fμ(xk+skdk)≤Fμ(xk)+cskFμ(xk)Tdk，

其中，sk>0，τ∈(0,1)。令xk+1=xk+skdk，可得xk+1。

若当前迭代点xk不满足粗糙条件(2)，则执行步骤3)，利用随机坐标下降算法[15]求解下一个迭代点xk+1，即每次通过随机选取j∈{1,2,…,n}进行更新。具体求解过程为：

令

p(x)=xk，

则

y-xk=(0,0,…,t,…,0)T，

此时，求解子问题

转变为求解一维问题

求得

t*=

然后计算p(x)+t*ej，便可使xk的第j个分量得到更新，循环此过程，直至满足停机准则，便可得到xk+1。

3 数值实验

为了验证算法1的有效性，将本算法的数值结果与邻近梯度法[16]、线搜索邻近梯度法[16]、加速邻近梯度法[17]、线搜索加速邻近梯度法[17]求解的数值结果进行比较。所有算法在MATLAB R2018a中运行，测试环境为Windows 10操作系统，Intel®CoreTMi7-10750H CPU @2.60 GHz，16 GiB。

求解问题(1)所用的数据集来源于https://www.csie.ntu.edu.tw/～cjlin/libsvmtools/datasets/binary.html。在求解问题(1)时，将最大迭代次数设为300，令N=7 366，n=300，ε=10-6，取初始点x0=zeros(n,1)，其中算法1中的子问题采用随机坐标下降法求解[25]，其它算法中的子问题使用阈值算子求解。图1为5种算法的相对目标函数值残差随迭代次数的变化情况，图2为相对误差随迭代次数的变化情况，表1为5种算法的运行结果比较。

图1 5种算法目标函数值相对误差变化

图2 5种算法迭代序列相对误差变化

表1 5种算法比较结果

由图1、2可知，当达到相同精度时,MRCDA算法所需的迭代次数最少。从表1可看出，在相同条件下终止迭代时，MRCDA算法运行时间最短。这表明，MRCDA算法在求解L1正则化L2损失支持向量机问题时是有效的。

4 结束语

针对L1正则化L2损失SVM问题，提出了一种多层随机坐标下降算法。首先判断当前迭代点是否满足粗糙条件(2)，若满足，则执行粗糙步，否则，执行随机坐标下降步。数值实验结果表明，该算法对求解L1正则化L2损失SVM问题是有效的，但关于算法收敛性的理论分析仍有待进一步研究。