具有脉冲促销的V-W模型的动力学分析
2022-07-08周观凤蒋贵荣
付 敏, 周观凤, 凌 琳, 蒋贵荣
(桂林电子科技大学 数学与计算科学学院,广西 桂林 541004)
广告在企业产品销售和促销中有着特殊的作用,是最快速、最大化、最广泛的传播媒介。为了推动消费者对商业产品的行为,企业可通过报纸、杂志、电视广告或邮件等各种传统大众媒体或网站、短信等新媒体发布广告信息,将产品与劳务的特征、功能、用途及生产厂家、销售价格等信息及时传递给消费者,减少消费者的搜寻成本,沟通供需双方之间的联系,引起消费者的注意与兴趣,促进产品销售。广告可以推动企业的发展,企业要在激烈的市场竞争中生存和发展,就要生产出符合广告宣传的高质量产品。广告可以刺激、诱导消费者的消费,甚至改变消费者的生活习惯,使潜在的消费需求变成现实的购买行动,并会创造出全新的需求。另外,广告也会扩大产品的知名度,获得消费者一定的信赖,树立良好的企业形象,创造并维持顾客的忠诚度,从而在一定程度上引起产品购买量的增加。广告是企业发展中不可或缺的手段之一,在开拓市场,争夺销量,创造经济利益等方面的作用不可小视。由于广告的上述功能和效应,很多企业借助广告而获得巨大成功,如:正是通过广告,在短短2年内伏特加酒成为美国酒类市场第一品牌;中国的“脑白金”保健品凭借广告也在短时间内获得巨大成功。广告对许多企业的生存和发展至关重要,无广告的企业在现在的社会很难生存与发展。
广告是一种营销策略,在一定销售时间段内,如何进行广告投入,以达到最好的经济效应,是广告研究的核心内容。为了对该问题有一个科学的分析,为决策提供理性参考,就必须建立相应的数学模型,并根据模型进行预测、决策。Nerlov Arrow(N-A)模型关注的是广告行为对品牌商誉度的影响[1]。文献[2]利用Vidale-Wolfe(V-W)模型研究了产品需求与广告投入之间的关系。很多学者在V-W模型的基础上根据不同情况提出了大量的扩展模型,取得了一些成果[3-4]。Lanchester模型可看作V-W模型在竞争环境下的延伸[5-7],文献[8]利用Lanchester模型分析了双寡头垄断企业的最优广告策略。Erickson[9]研究了双寡头市场上公司的最优广告投入,并得出动态广告竞争问题的闭环纳什均衡解。Chintagunta[10]采用理论和实证相结合的方法,借助Lanchester模型分析双寡头市场上企业的动态广告竞争,得出该模型的闭环和开环纳什均衡解,并比较了这2种均衡结果。通过微分对策方法研究广告竞争较早的学者是Deal[11],他将V-W模型进行了扩展,研究了双寡头市场公司的最优广告投入,并通过数值模拟对模型进行了计算。Bass等[12]将广告进一步分为通用广告和品牌广告,企业利用通用广告增加了产品的需求量,同时利用品牌广告争夺市场份额,通过对称和非对称2种情况研究了双寡头市场中公司的最优广告策略。Sorger[13]在Sethi的基础上结合Lanchester模型进行扩展。Leitmann等[14]研究了两企业之间的竞争问题,企业目标是利润最大化,公司的市场份额受自身及竞争者双方广告的影响。Erickson[15]从广告竞争中的微分对策的角度讨论了动态模型。
V-W模型具有广泛的吸引力,因为它是在经验证据的基础上发展起来的,且对实际应用具有灵活性。该模型通过一个微分或差分来表示销售变化率与广告结转效应之间的直接关系。考虑到真实市场的竞争因素,Kaszkurewicz[16]建立的模型描述了任意非负初始条件下市场份额的动态变化,从而扩展了经典的Vidale-Wolfe模型。
促销是一种盈利手段,目的是在短时间内寻求增加企业产品销量的方法。企业促销的形式主要有人员促销、广告促销、公关促销、网上促销、服务促销等。每当进行打折、团购等促销活动或者某些节日时,市场需求在短时间内激增,使得订单量出现较大波动。这种短时间内需求激增的现象称为脉冲效应。Jiang等[17]讨论了促销对互联网的影响,发现促销参数可以通过倍周期分岔来影响广告模型的稳定性并导致混沌。文献[18]的研究表明,促销与购买意愿及销售有显著关系,其中样本类型、促销产品数量和样本量部分地调节了促销与短期或长期效应之间的关系。文献[19]构建了基于多项式Logit模型的快速消费品促销评估模型,验证了快速消费品促销效果评估模型的可行性,该评估模型有助于企业优化资源和提高经济效益。
市场中2个竞争企业都采用脉冲促销来提高销量时,周期解的存在和稳定意味着市场不会出现盲目竞争。鉴于此,将广告竞争与脉冲促销引入V-W模型,讨论销量的变化,特别是周期解的存在性和稳定性。
1 模型描述
为了考虑广告竞争的动态问题,Vidale和Wolfe构建了以下V-W模型:
其中:αi为衰减常数;Ni(t)为企业i在t时刻的销售水平;ui(t)为企业i在t时刻的广告支出;ri为广告的反应速率;M为市场的饱和程度。
当企业广告投放为固定的投入时,采用双寡头垄断的V-W模型,研究2个企业生产的相同产品的销售量:
(1)

假设
W1>W2>0,α1<α2,
(2)
W1>W2表示企业1的广告投放效果优于企业2的广告投放效果,α1<α2表示企业1的衰减常数小于企2的衰减常数。
方程组(1)的唯一正平衡点
A(N1A,N2A)=
在条件(2)下,得到N1 A>N2 A,则可通过直接计算得到方程组(1)相应的特征多项式:
λ2+(W1+α1+W2+α2)λ+
α1α2+α1W2+α2W1,
(3)
故其对应的特征值为
利用λ1λ2>0,λ1+λ2<0的情况,可推出λ1<0,λ2<0的情况,得到方程组(1)的平衡点A(N1 A,N2 A)是稳定的节点。
为了增加销量,企业1、2通过定期举办促销活动增加销量:
N1(nT+)=N1(nT)+h,
(4)
N2(nT+)=N2(nT)+c(M-N2(nT))2,
(5)
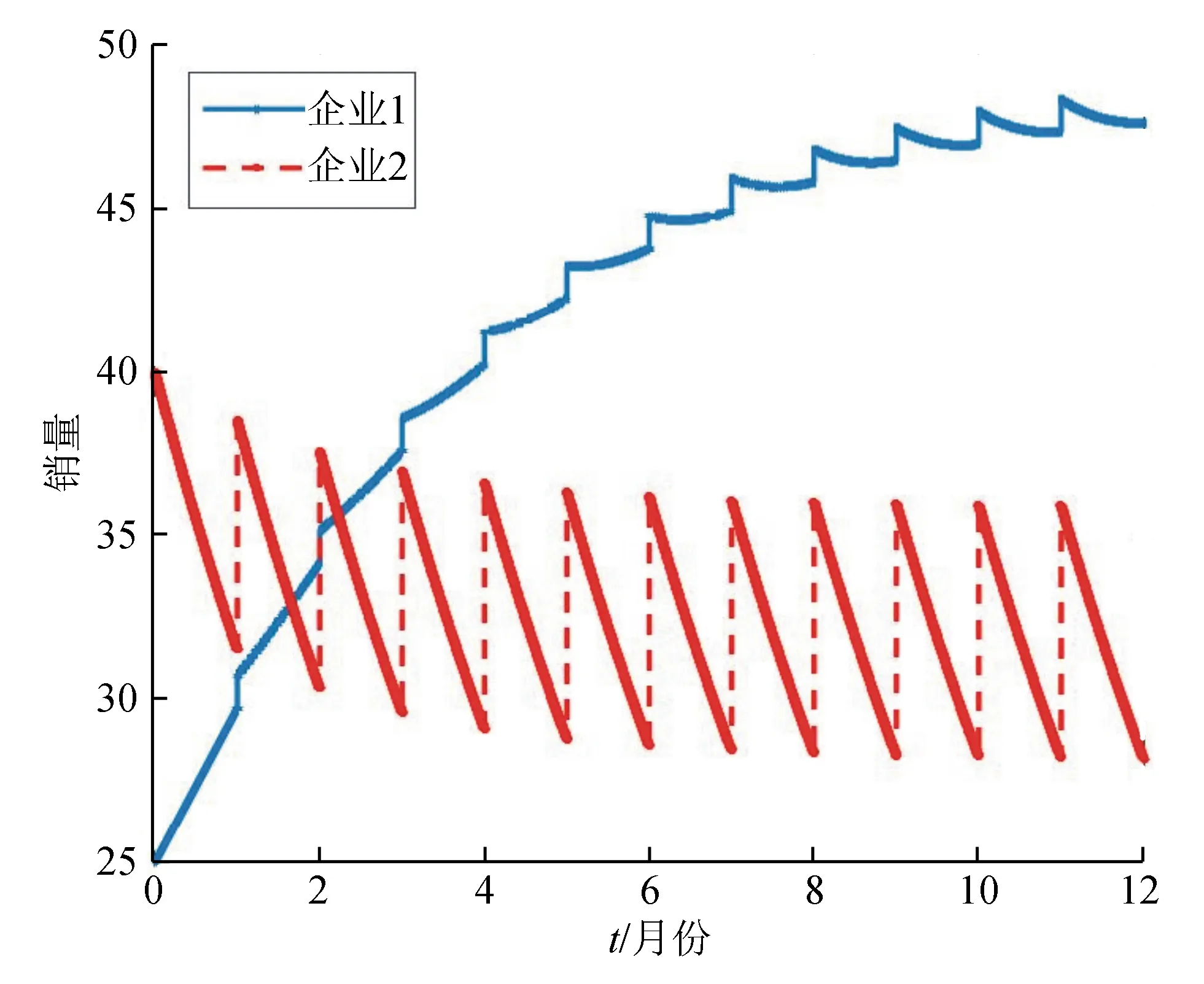
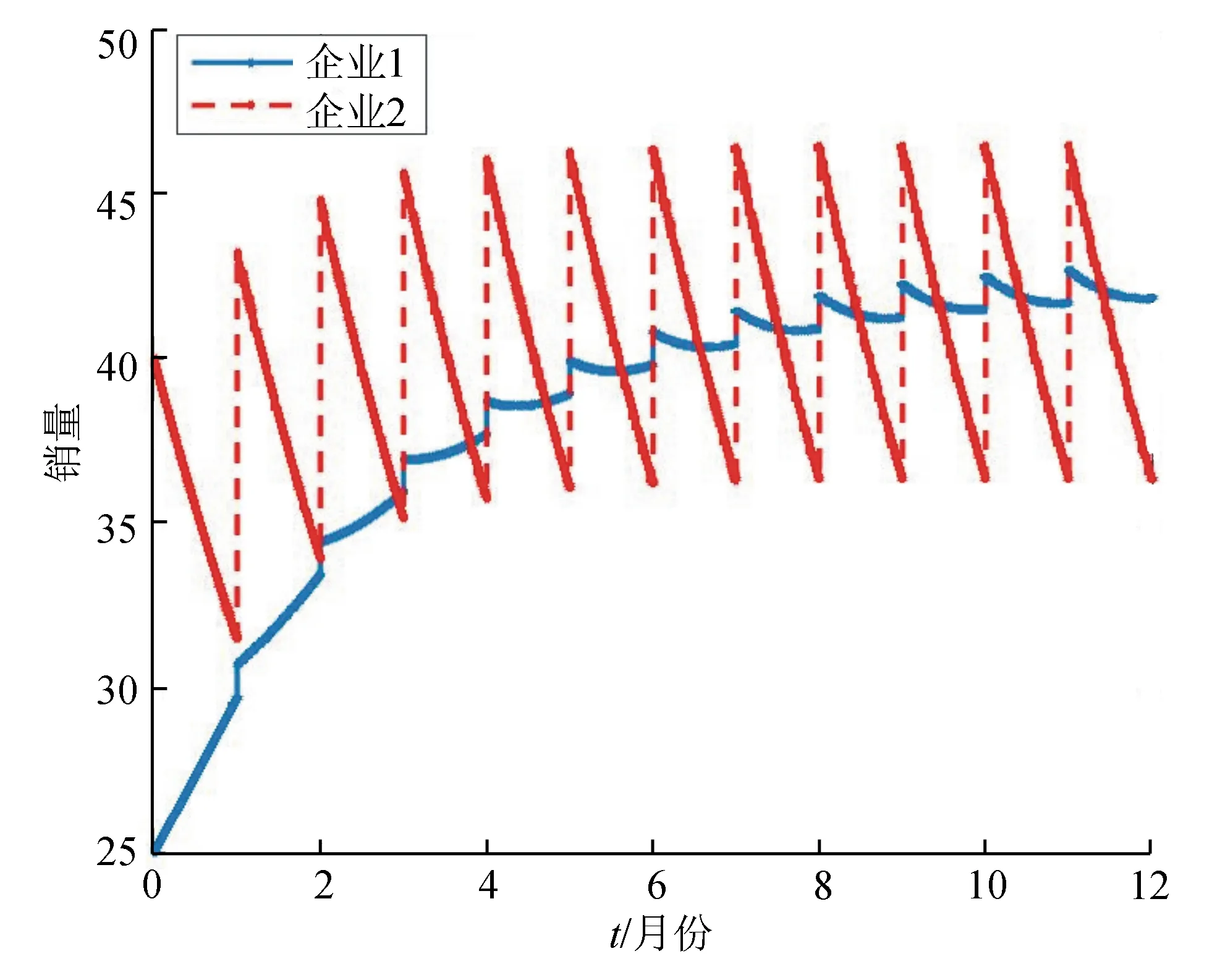
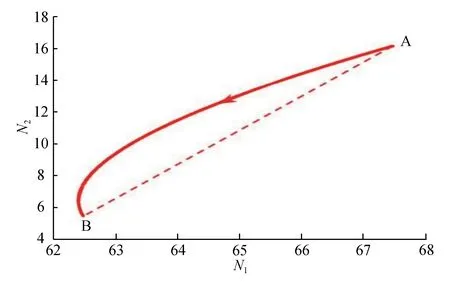
其中:0 (6) 根据对销量的分析及推导可得式(1)的一般解: (7) 其中:e为方程的基础解系; 设初始点为(N1(0),N2(0)),根据式(7)可得: 为便于计算,假设 α1+W1=α2+W2,W1=βW2, (8) 则式(1)过初始点(N1(0),N2(0))的解为 整理后,可得2个企业在时间[0,T]的销量: (9) F1(t)=(1-h1(t))N1A+h2(t)βN2A; 根据式(9)可计算企业1、2在时刻T时的销量N1(T)、N2(T),这时实施脉冲促销。由式(6)的第3个和第4个式子,可得促销后的销量为N1(T+)、N2(T+),从而2个企业在时间(0,2T]的销量为 类似地,可得2个企业在时间(nT,(n+1)T]的销量变化情况。 若销量能周期性变化,则有利于市场稳定。假设式(6)的轨迹在t=kT处到达点Ak(xk,yk),由于促销的作用,跳跃到点Ak+(xk+,yk+),在t=(k+1)T时到达点Ak+1(xk+1,yk+1),其中 xk+=xk+h,yk+=yk+c(M-yk)2, 则可得离散映射: (10) 设式(6)的不动点为A0(x0,y0),由式(10)有 (11) 解之得 (12) 其中: F5=h1βcM2-h2(Z+h)+F2β; G(c)=2cMh1β-βh1+β-h2B。 式(10)的不动点A0(x0,y0)对应式(6)的周期T-解: (13) 其中,nT 计算不动点A0(x0,y0)的特征多项式: 用λ1A0、λ2A0表示不动点A0(x0,y0)的特征值,则不动点A0(x0,y0)稳定的条件为|λ1A0|<1,|λ2A0|<1,从而有 解之得 (14) 因此,当式(14)成立时,不动点A0是稳定的,进而式(6)的正周期T解是稳定的。故有如下结论: 定理1 若式(8)、(14)成立,则式(6)具有唯一稳定的周期T解,其解如式(13)所示。 考虑模型 (15) 其中:M=100,α1=0.1,α2=0.25,W1=0.2,W2=0.05。 取初始点(25,40),T=1,h=1时,企业1的促销力度不大。取c=15/10 000,根据销量计算公式可得2个企业的销量的变化。图1为T=1,h=1,c=0.001 5时,企业产品的销量变化曲线。从图1可看出,企业1的销量从25开始增加,会大于企业2的销量。图2为T=1,h=1,c=0.002时,企业产品的销量变化曲线。从图2可看出,企业2增大促销力度,可使得销量在一定程度上保持优势。 图1 T=1,h=1,c=0.001 5时,企业产品的销量变化 图2 T=1,h=1,c=0.002时,企业产品的销量变化 取T=5,h=5,c=0.001 2,根据式(13),可得式(15)的周期解,如图3所示。系统的轨线从点A(67.477,16.168 1)出发,经过5个月后,到达点B(62.477,5.1437 6)。2个企业都进行促销活动,销量增加,系统的轨线跳跃到点A,从而得到周期解。 图3 T=5,h=5,c=0.001 2时,系统(15)的周期解 容易验证式(14)成立,根据定理1可得图3的周期解是稳定的,从其附近出发的轨线会无限趋于周期解。图4为T=5,h=5,c=0.001 2时,系统(15)的销量变化曲线。从图4可看出,从点(50,15)出发的轨线趋向于周期解。 图4 T=5,h=5,c=0.001 2时,企业产品的销量变化 考虑促销,建立了一个广告竞争模型。理论分析了销售同样产品的2个企业的销量随促销的变化情况,利用离散映射得到周期解的存在性和稳定性的充分条件,数值例子说明了理论分析的正确性。 根据销量的计算公式和数值结果,可以让企业了解双方的市场占有份额,根据双方的情况确定促销力度,保持竞争优势或增加促销力度反超竞争对手。 广告竞争模型具有稳定的周期解,可保持市场的有序竞争,避免混乱的市场行为。虽然企业的销量在变化,但具有周期性,可让企业知晓大致的周期,以免引起恐慌。 本研究只考虑了双寡头垄断市场的2家企业的单一产品的促销策略,未考虑市场中其它竞争对手的销售,留待以后进一步研究。2 销量计算

3 周期解及其稳定性
4 数值模拟

5 结束语
