基于KF-BA-LSSVR的无线传感器网络节点定位研究

束仁义 朱家兵 沈晓波 蔡 俊 夏 泐

(淮南师范学院 电子工程学院， 安徽 淮南 232038)

0 前 言

通过中国北斗卫星导航系统(BDS)或者美国全球定位系统(GPS)可以实现户外目标定位；但对于室内、井下、管道等封闭空间，很难通过BDS或者GPS实现准确定位[1]，且成本高。因此，可以预先布置无线传感器网络(wireless sensor network，WSN)节点，使用成熟的定位算法来实现精准定位[2]。近年来，WSN在矿井人员定位、室内移动目标定位、天然气管道泄露定位等方面得到了广泛应用。许多学者提出了一些改进定位算法，如Thimmaiah等人提出了一种基于无线电信号强度的WSN定位误差优化技术[3]；Chen等人提出了基于WSN距离相关的室内迭代定位算法[4]；Lv等人提出了基于GA-PSO-BP混合算法的室内三维空间WSN定位技术[5]。2002年Suykens等人提出了基于最小二乘支持向量回归机(least square support vector regression, LSSVR)算法[6]。周松斌等人将LSSVR算法应用到WSN定位中，有效降低了估计误差对定位精度的影响，减小了平均定位误差[7]。张烈平等人提出了基于粒子群优化LSSVR的三维WSN节点定位算法，与LSSVR算法相比，该算法定位精度更高[8]。钟阳晶等人提出了基于RSSI高斯滤波的LSSVR定位算法，定位误差比未进行高斯滤波处理减少了12%～20%[9]。Zhang等人提出了基于RSSI-TOA和LSSVR算法的WSN节点三维定位算法，该算法比基于LSSVR或RSSI-TOA算法的定位精度更高[10]。

支持向量机是基于统计学习理论的机器学习算法，而LSSVR算法是基于支持向量机的一种改进[11]。本次研究是在LSSVR定位算法的基础上，采用蝙蝠算法(BA)和卡尔曼滤波算法(KF)，以提高节点定位精度。通过仿真实验对 LSSVR、基于蝙蝠算法的最小二乘支持向量回归机(BA-LSSVR)与基于卡尔曼滤波和蝙蝠算法的最小二乘支持向量回归机(KF-BA-LSSVR)等3种算法的定位结果，以及基于卡尔曼滤波的最小二乘支持向量回归机(KF-LSSVR)与KF-BA-LSSVR的平均定位误差进行了对比分析。

1 LSSVR定位原理

最小二乘支持向量回归机优化问题的数学模型如式(1)所示[12]：

(1)

式中：ω—— 权重矩阵；

bk—— 偏差；

ξk—— 拟合误差；

P—— 虚拟节点数量；

C—— 大于0的正则化参数；

φ(xk) —— 非线性映射函数。

径向基函数(radical basis function, RBF)选择高斯核函数[13],表达式如式(2)所示：

(2)

式中：Rm,Rn—— 输入向量，m、n=1,2,…,P；

σ—— 高斯核标准差。

通过拉格朗日乘子法得到式(1)所示拉格朗日函数：

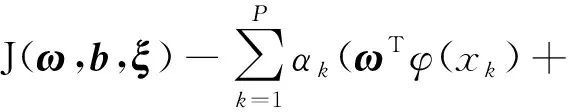
bk+ξk-yk)

(3)

式中：αk—— 拉格朗日乘子。

由式(3)分别对ω、b、α、ξ求导可得：

(4)

式中：I为单位矩阵；y=[y1,y2,…,yk]；e=[1,1,…,1]T；α=[α1,α2,…,αk]；Ω=Q(Rm,Rn)。

由式(4)可得：

(5)

式中：A=Ω+C-1I，由于|A|≠0，故A-1存在。

由式(5)得到最优决策函数：

(6)

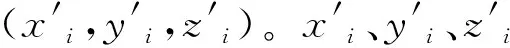
(1) 首先将dkj和xk作为输入训练样本量，此时dkj与xk分别对应式(1)中的φ(xk)和yk，同时对dkj与xk进行标准化处理；然后求得bk和αk。

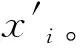
基于LSSVR的定位流程如图1所示。考虑实际定位存在偏差，节点平均定位误差为：

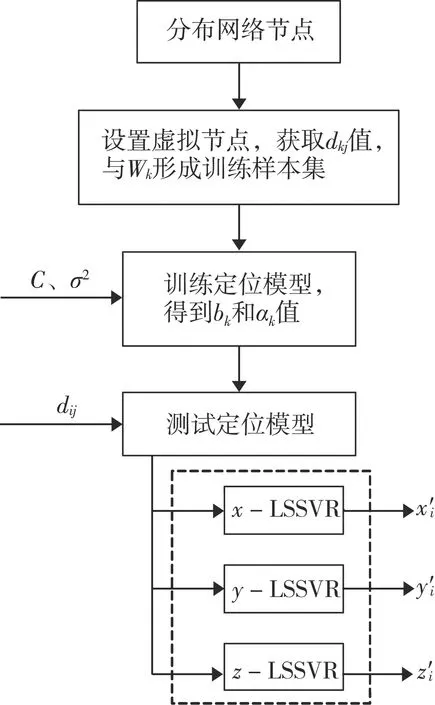
图1 基于LSSVR的定位流程

(7)

2 蝙蝠算法的参数优化

设正则化参数C和高斯核标准差σ的取值范围分别为[0.1,100.0]和[0.1,10.0]。由于确定参数值需要满足定位环境的要求，因此提出一种基于BA算法的优化方法。BA算法是Yang等人于2010年提出的一种新型群体智能算法[14]，在求解全局最优解等方面具有很好的效果。

假设在一个D维搜索空间中，存在一定数量的蝙蝠，每个蝙蝠在某个位置以一定速度飞行且具有不同频率。设最大脉冲音量和最大脉冲率分别为G和U。

已知第i个蝙蝠在t时刻的位置、飞行速度和频率分别为Xi,t、Vi,t和Fi,t，则有[15]：

Fi,t=Fmin+β(Fmax-Fmin)

(8)

Vi,t+1=Vi,t+Fi,t(Xi,t-X*)

(9)

Xi,t+1=Xi,t+Vi,t+1

(10)

式中：β—— 服从均匀分布的随机变量，取值范围为[0,1)；

X*—— 当前全局最优解。

蝙蝠在空间搜索过程中根据需要调整G和U,更新公式为：

Gi,t+1=λGi,t

(11)

Ui,t+1=Ui,0(1-exp(-γt))

(12)

式中：λ、γ—— 常数，0<λ<1、γ>0。

根据BA算法原理，优化正则化参数C和高斯核标准差σ的步骤如下：

(1) 初始化蝙蝠参数，主要包括种群数、Fmin、Fmax、Xi,t、Vi,t、G和U等。

(2) 定义蝙蝠个体的适应度函数为：

(13)

首先将C和σ代入LSSVR定位算法中，再将定位结果代入式(13)中进行求解，得到Fitness*。

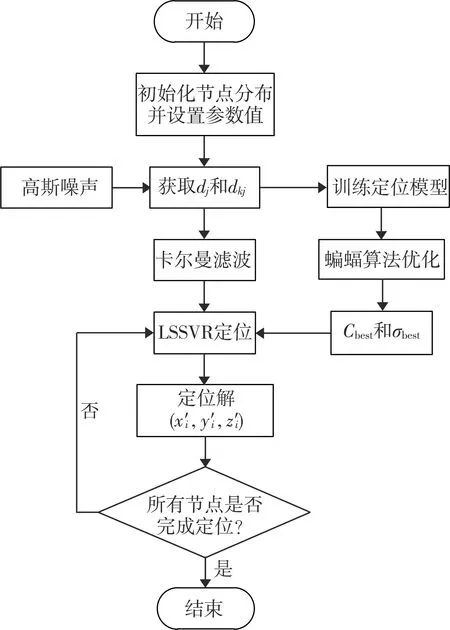
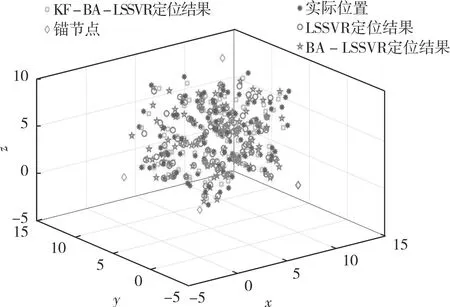
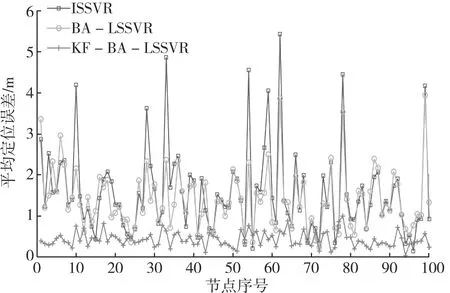
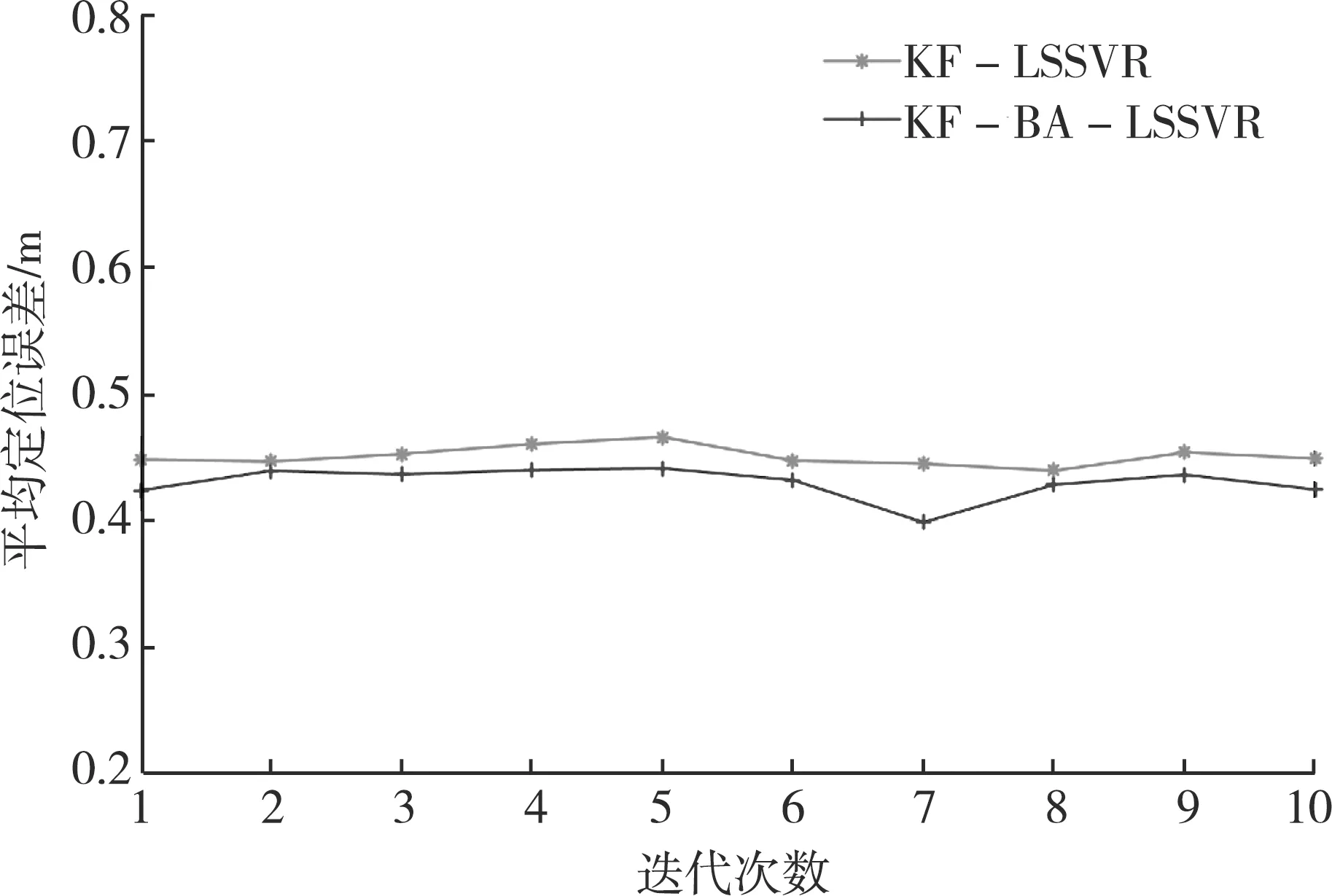
(3) 将步骤(1)和(2)中参数值代入式(8) — 式(10)中，得到C*和σ*。比较最大脉冲率U和均匀分布随机数rand，如果U

C=C*+λG

(14)

σ2=(σ*)2+λG

(15)

如果C和σ超出设定范围，则取临界值。

(4) 重复步骤(2)和(3)，如果Fitness>Fitness*,计算得到当前全局最优解Cbest和σbest。

(5) 进行多次迭代，重复步骤(2) — (4)，得到最终优化的C和σ。

3 卡尔曼滤波定位

作为输入测试变量，距离对LSSVR定位的精度有很大影响，在实际测距过程中容易受到环境的影响。为了提高测距精度，在高斯白噪声模型下采用KF算法进行距离优化，具体描述如下[16-17]：

(1) 状态一步预测：

(16)

式中：δ—— 离散时间；

Φ—— 状态转移矩阵；

(2) 一步预测协方差矩阵：

P(δ+1|δ)=ΦP(δ|δ)ΦT+S

(17)

式中：S—— 噪声协方差矩阵；

P(δ|δ) —— 上一状态的协方差矩阵，设P(0|0)=P0。

(3) 滤波增益矩阵：

K(δ+1)=P(δ+1|δ)HT×

[HP(δ+1|δ)HT+E]-1

(18)

式中：H—— 观测矩阵；

E—— 噪声驱动矩阵。

(4) 状态更新：

K(δ+1)ε(δ+1)

(19)

(5) 协方差矩阵更新：

P(δ+1|δ+1)=[I-K(δ+1)H]×

P(δ+1|δ)

(20)

通过式(1) — 式(5)进行迭代更新，减小高斯白噪声对距离的影响，提高节点定位精度。基于 KF-BA-LSSVR的定位流程如图2所示。

图2 基于KF-BA-LSSSVR的定位流程

4 仿真实验

4.1 仿真环境

表1 BA算法参数设置

按照图2所示定位流程进行仿真实验，对LSSVR、BA-LSSSVR和KF-BA-LSSSVR等3种算法的定位结果及节点平均定位误差(见图3、图4)进行对比分析。经过BA算法优化后得到C=41.836 7、σ2=2.812 3。经过BA算法优化后，LSSVR定位误差减小，而经过卡尔曼滤波后，其定位误差更小。

图3 3种算法的定位结果

图4 3种算法的平均定位误差

在参数相同的仿真环境下分别迭代10、20、30次，根据式(7)得到平均定位误差。由3种定位算法不同迭代次数的误差对比结果(见图5)可知，增加迭代次数没有提高节点的平均定位精度。

图5 3种算法不同迭代次数的平均定位误差对比

在参数相同的仿真环境下，迭代10次，得到 KF-LSSVA和KF-BA-LSSVR的平均定位误差曲线(见图6)。KF-BA-LSSVR算法的平均定位误差比KF-LSSVR算法小。

图6 KF-LSSVR和KF-BA-LSSVR的

5 结 语

为进一步提高基于LSSVR算法的WSN定位精度，提出基于BA算法的LSSVR算法。仿真实验结果表明,基于BA算法的LSSVR定位效果得到了改善。在考虑测量距离受高斯噪声影响的情况下，采取卡尔曼滤波进行距离优化后，定位精度明显提高、定位误差大幅降低。在LSSVR定位的基础上,通过BA优化正则化参数和高斯核标准差,采用卡尔曼滤波算法降低噪声对测距的影响，为WSN三维节点定位提供了一种良好的途径。