一种基于Canny边缘检测算法的零件缺陷图像处理方法

石冬阳 张俊林 杨 欣 聂翱翔 张雨欣 庞迎春

(重庆科技学院 电气工程学院， 重庆 401331)

0 前 言

在零件的加工过程中，由于机器老化、机器自身存在偏差、生产技术等原因，常常导致加工出来的产品质量存在问题[1-2]。不合格的产品直接影响仪器设备的正常使用，因此，零件质量的检测尤其重要。

近年来，随着图像处理与深度学习技术的发展，出现了多种针对零件螺纹缺陷检测的方法，很大程度地提升了零件的产品合格率。文献[3]报道了利用机器视觉皮带开发，实现了对3种螺纹缺陷的检测，但该方法没有考虑图像噪声对检测结果的影响。文献[4]中，首先采用Roberts算法对零件图像进行预处理，然后对螺纹边缘进行特征提取，其不足之处在于，检测的螺纹边缘存在断裂、漏检的现象。文献[5]中，采用机器视觉工件缺陷检测系统对螺纹缺陷进行了定位，但其能够检测的螺纹缺陷类型不全。文献[6]中，提出了局部投影统计法，该方法能够快速有效地去除图像噪声，但能够检测出的螺纹缺陷类型也不全。

1 缺陷检测模型的构建

首先，对零件图像进行灰度化、二值化、锐化等预处理；然后，采用边缘检测、直线检测、图像旋转、垂直投影等方法对零件的螺纹缺陷进行检测。零件螺纹缺陷检测流程如图1所示。

图1 零件螺纹缺陷检测流程图

2 图像预处理

为了使螺纹图像特征更加明显，避免图像噪声的干扰，需要对其进行预处理，以提高螺纹缺陷检测的精度。

2.1 图像灰度化

对图像进行灰度化操作，可以减少运算量。取3个分量的最大值，作为图像灰度化处理的结果，如式(1)所示：

Gray(i，j)=max[R(i，j)，G(i，j)，B(i，j)]

(1)

式中：Gray(i，j)表示图像灰度值；R(i，j)、G(i，j)、B(i，j)分别表示图像的3个分量。

2.2 图像二值化

目标图像与背景图像的灰度值有较大差异，根据灰度值对其进行区分。将目标图像灰度值标记为 0，将背景图像灰度值标记为1，设F(x，y)为图像中像素点的灰度值，灰度阈值(Th)的变换函数为[7-8]：

(2)

2.3 图像锐化

为了使零件边缘特征更加明显，采用Sobel算法对图像进行锐化，如式(3) — 式(5)所示：

Hx=(z7+2z8+z9)-(z1+2z2+z3)

(3)

Hy=(z3+2z6+z9)-(z1+2z4+z7)

(4)

|▽f|≈|Hx|+|Hy|

(5)

式中：Hx和Hy分别表示像素点横向、纵向梯度近似值；|▽f|表示图像梯度幅值；z1—z9表示原图像与模板矩阵相乘所对应的各像素点。

3 零件螺纹缺陷检测

零件螺纹缺陷检测的步骤主要包括：边缘检测、直线检测、水平旋转、垂直投影等。其中，边缘检测的效果将直接影响缺陷检测的精度，Canny算法具有滤波降噪的结构，并可以通过设定高低阈值，对图像真实和虚假边缘进行有效区分，可避免发生断裂、漏检的现象。

3.1 边缘检测

对目标图像进行边缘检测，可以得到图像的形状和特征，Canny边缘检测算法包括以下4个步骤[9-10]：

(1) 滤波操作。使用高斯滤波器进行滤波操作，从而减轻噪声对边缘检测的影响。对图像进行卷积处理，选用的高斯分布函数为：

(6)

式中：σ表示高斯滤波器的参数。

原图像I(x,y)与高斯分布函数S(x,y)卷积后，得到图像H(x,y)：

H(x,y)=S(x,y)×I(x,y)

(7)

(2) 图像梯度幅值与方向的计算。图像梯度幅值可呈现图像像素的变化，梯度方向代表了图像像素强度变化的方向。像素点(i,j)在x、y方向的偏导数wx(i,j)和wy(i,j)分别为：

wx(i,j)=[I(i,j+1)-I(i,j)+

I(i+1,j+1)-I(i+1,j)]/2

(8)

wy(i,j)=[I(i,j)-I(i+1,j)+

I(i,j+1)-I(i+1,j+1)]/2

(9)

此时，像素点(i,j)处的梯度幅值w(i,j)和梯度方向θ(i,j)分别为：

(10)

(11)

(3) 非最大值抑制。非最大值抑制的操作过程是先确定梯度方向的非零点，然后沿该点的方向导数寻找邻近的2个点。若2个邻近点的幅值超过中心点，那么此非零点不属于图像边缘，则令其边缘强度为0。

(4) 双阈值选取和边缘连接。通过设定高、低阈值，可对图像真实和虚假边缘进行有效区分，最终只保留真实有用的边缘信息，可以很好地抑制伪边缘的存在。

3.2 直线检测

在笛卡尔坐标系中，直线的表达式为y=ax+b。其中，a表示直线斜率；b表示该直线在y轴的截距。在极坐标系中，直线的表达式为xcosθ+ysinθ=ρ。其中，ρ表示该直线与原点之间的距离；θ表示该直线法线的切线斜率。根据直线的平移和旋转特征，平行放射线束的投射可由一组平行线的模型来实现。沿着直线xcosθ+ysinθ=ρ的射线，能够得出投射数据中的任何一点。设f(x,y)为平面图上一任意连续函数，Radon变换定位可表示为：

Radon(f(x,y))=λ(ρ,θ)

=∬f(x,y)δ(xcosθ+ysinθ-ρ)dxdy

(12)

式中：λ(ρ,θ)表示Radon变换的结果；δ()表示冲击函数，只有在其变量为0时，才为无穷大值，其积分结果为1。

当x、y的值处于离散状态时，Radon变换定位可表示为：

Radon(f(x,y))=λ(ρ,θ)

(13)

式中：m、n分别表示图像的高度和宽度；x、y、ρ、θ分别表示离散变量。

3.3 图像旋转

对零件图像进行直线检测后，需要对其进行水平旋转。以直线检测结果中若干条直线斜率的平均值作为水平旋转的角度，常用的计算公式如式(14)所示：

(14)

式中：gθ表示水平旋转角度；hi表示直线的斜率；n表示检测直线的数量。

3.4 垂直投影

垂直投影能够反映物体形状变化的规律，是识别物体缺陷的重要方式。正常螺纹与有缺陷螺纹的垂直投影图有所差异，可据此判断螺纹缺陷的位置。

4 仿真验证

4.1 图像预处理结果

通过MatlabR 2018软件分别对正常螺纹、半螺纹、不规则螺纹、无螺纹等4种螺纹零件图像进行预处理，结果如图2所示。经过预处理的图像，边缘特征更加容易提取，噪声影响较低。

图2 螺纹零件图像预处理结果

4.2 缺陷检测

4.2.1 6种边缘检测效果

分别采用Roberts、Sobel、Prewitt、LOG、Canny、数学形态学等6种边缘检测算法，对零件螺纹边缘进行检测，通过MatlabR 2018软件进行仿真模拟，对比不同算法的检测效果。其中，对于Roberts、Sobel、Prewitt等3种算法，其阈值设定为0.050 0，模拟结果如图3 — 图5所示。LOG属于二阶微分算法，其阈值设定为0.055 0，模拟结果如图6所示。对于Canny边缘检测算法，高低阈值分别设定为0.265 6、0.106 3，模拟结果如图7所示。对于数学形态学的边缘检测方法，本次采用3×3模板，模拟结果如图8所示。

图3 Roberts边缘检测算法模拟结果

图4 Sobel 边缘检测算法模拟结果

图5 Prewitt边缘检测算法模拟结果

图6 LOG边缘检测算法模拟结果

图7 Canny边缘检测算法模拟结果

图8 数学形态学边缘检测算法模拟结果

由模拟结果可知，采用Roberts、Prewitt、Sobel检测出的螺纹边缘存在断裂、漏检的现象。其中，Prewitt、Sobel算法的漏检现象较为严重，图像边缘的完整性较差。采用LOG、数学形态学算法检测出的螺纹边缘出现了虚假边缘。比较而言，Canny算法在噪声的抑制、检测边缘的连续性、检测目标的细节等方面都具有明显优势。

4.2.2 Canny算法的检测结果

利用Canny算法对预处理后的图像边缘进行检测，结果如图9所示。正常螺纹零件边缘检测结果呈规律性波动；半螺纹零件部分边缘检测结果呈规律性波动；不规则螺纹零件边缘检测结果呈无规律波动；无螺纹零件边缘检测结果呈直线。

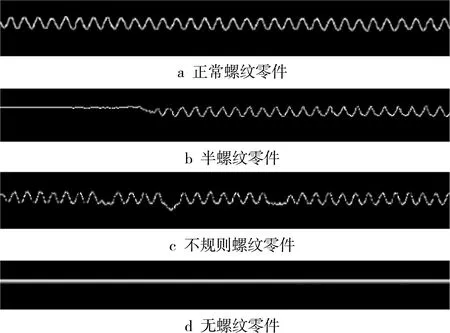
图9 螺纹零件边缘检测结果

4.2.3 直线检测结果

本次研究采用Radon算法对4种螺纹零件进行直线检测，结果如图10所示。4种螺纹零件所在的直线都能被准确地检测出来，与实际情况相一致。这说明Radon算法能够准确检测零件中直线所在位置。

图10 螺纹零件直线检测结果

4.2.4 水平旋转结果

为了使螺纹零件图像处于水平位置，需要对图像进行水平旋转。根据直线检测结果，计算零件所在直线的斜率，取若干条直线斜率的平均值，得到直线旋转的角度，结果如图11所示。

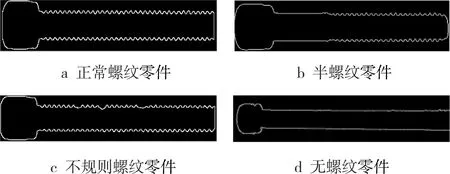
图11 螺纹零件水平旋转结果

4.2.5 垂直投影结果

通过垂直投影可以直观地观察到正常螺纹与缺陷螺纹的区别。对水平旋转后的边缘检测图进行垂直投影，结果如图12所示。正常螺纹零件的垂直投影的波形在一定幅值范围内呈规律性波动，不存在水平波动的现象。存在缺陷的螺纹零件与正常零件的垂直投影图在波形形状、波动幅值上有较大差别，可由此判断零件螺纹缺陷的类型。

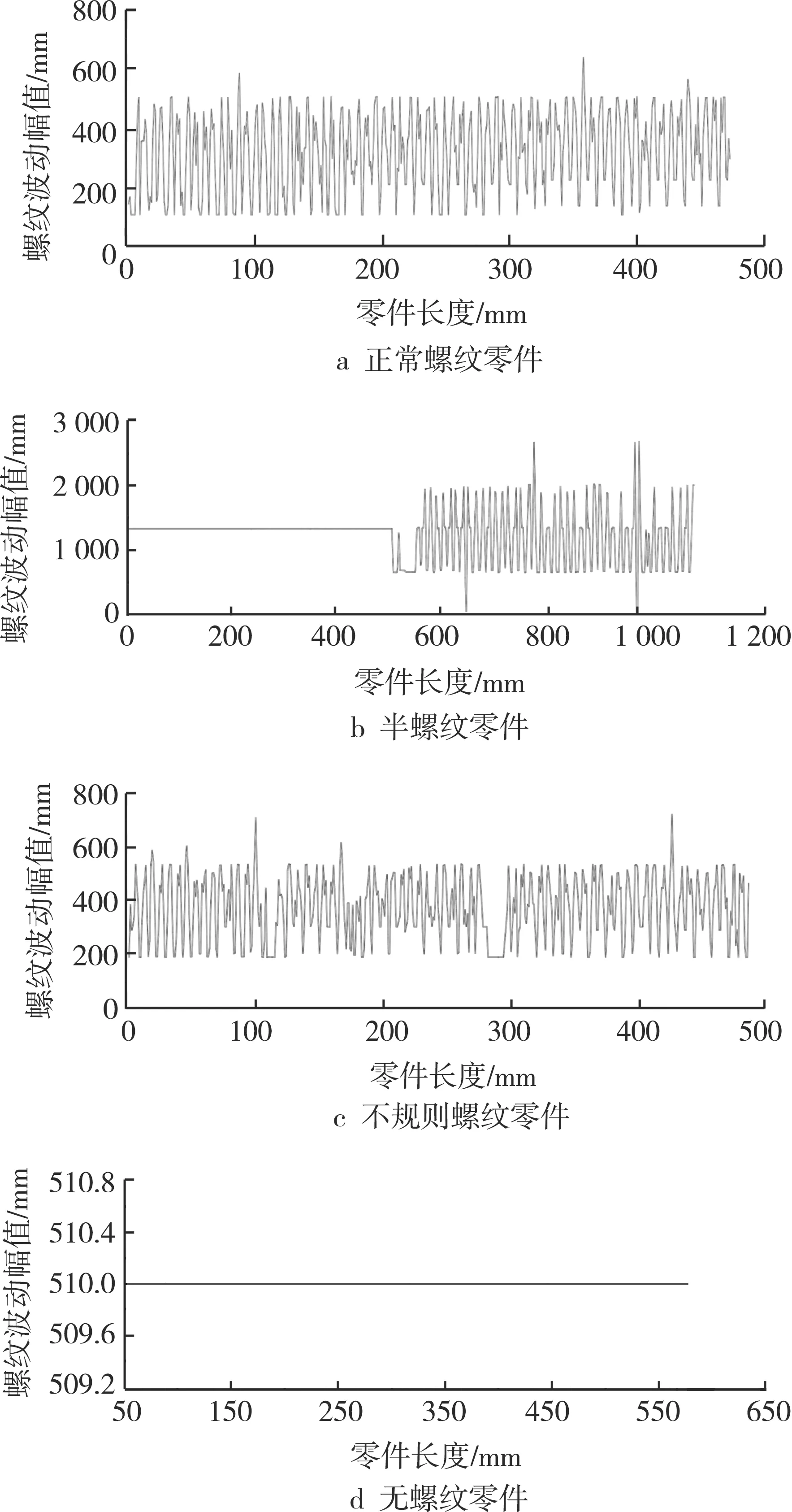
图12 螺纹零件垂直投影结果

5 结 语

本次研究以准确检测出零件上的螺纹缺陷为目的。首先对零件图像进行灰度化、二值化、图像锐化等预处理，使检测目标的边缘特征更加容易提取；然后，利用边缘检测、直线检测、图像旋转和垂直投影等方法对螺纹缺陷进行检测。采用Canny算法可避免检测过程中发生断裂、漏检的现象，能够有效提高螺纹缺陷检测的精度。