零点存在性定理中的“取点”问题
2022-07-08361000厦门市海沧区教师进修学校附属学校陈志康
361000 厦门市海沧区教师进修学校附属学校 陈志康
361026 厦门双十中学海沧附属学校 陈雨瑾
在解决零点存在性问题时,常常需要结合图形来分析,但由于学生没有学习过函数极限,无法分辨一些函数图像在无穷远处或间断点处的性态.如果想要严格说明零点的存在,只能借助零点存在性定理,即若f(x)在[a,b]上是一条连续不断的曲线,并且有f(a)·f(b)<0,则存在c∈(a,b),使得f(c)=0,适当“取点”来说明函数值的正、负.在一些试卷公布的答案中,并没有对如何“取点”进行特别说明,很多学生不能明白其精髓所在.正确“取点”要求具备较高的数学核心素养,以此为抓手提升学生的逻辑推理、数学运算能力正合适不过,如果能解决这些问题,对学生今后学习“极限”这部分的内容也会有所帮助.笔者阐述解决这些问题过程中获得的感悟.
例1(2017全国卷Ⅰ理-21) 已知函数f(x)=ae2x+(a-2)ex-x,a∈R.
(1)讨论f(x)的单调性;
(2)若f(x)有两个零点,求a的取值范围.
小问(1) 分析:可知f′(x)=2ae2x+(a-2)ex-1,结合式子的结构特征,因式分解为f′(x)=(2ex+1)(aex-1),接下来只需考虑aex-1的符号问题即可得到结果.
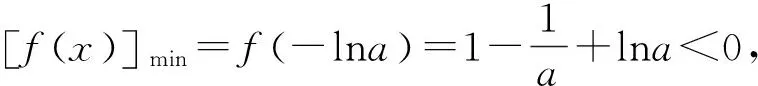

注意到f(x)=ae2x+(a-2)ex-x,0
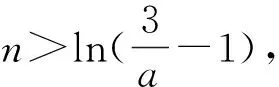
事实上,“取点”是经过适当“放缩”计算得出的,常见的不等式如当x>0时,有ex>x>lnx.笔者总结得出以下“取点”技巧.
(1)借助一些常见不等式对超越式放缩,放缩后的不等式容易解出.
(2)不等式放缩的方向要与所需函数值的正负一致,如上述找n的取值需要f(n)>0,对f(n)中一些式子放缩要往“>”的方向进行.
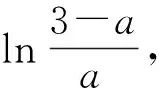
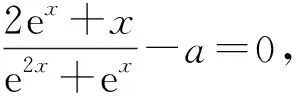
下证充分性(只需在y轴左侧找一点的函数值为负,在y轴右侧找一点的函数值也为负,例如找到x0<0使得g(x0)<0).
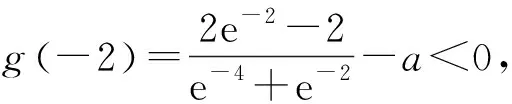

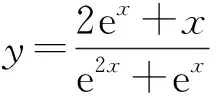

图1
例2(2015全国卷Ⅰ文-21) 设函数f(x)=e2x-alnx.
(1)讨论f(x)的导函数f′(x)的零点个数.(2)略.
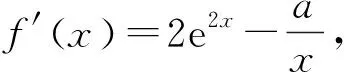
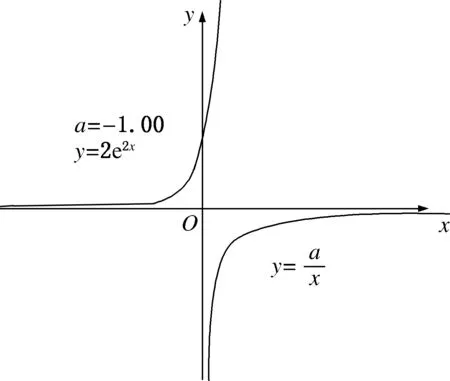
图2
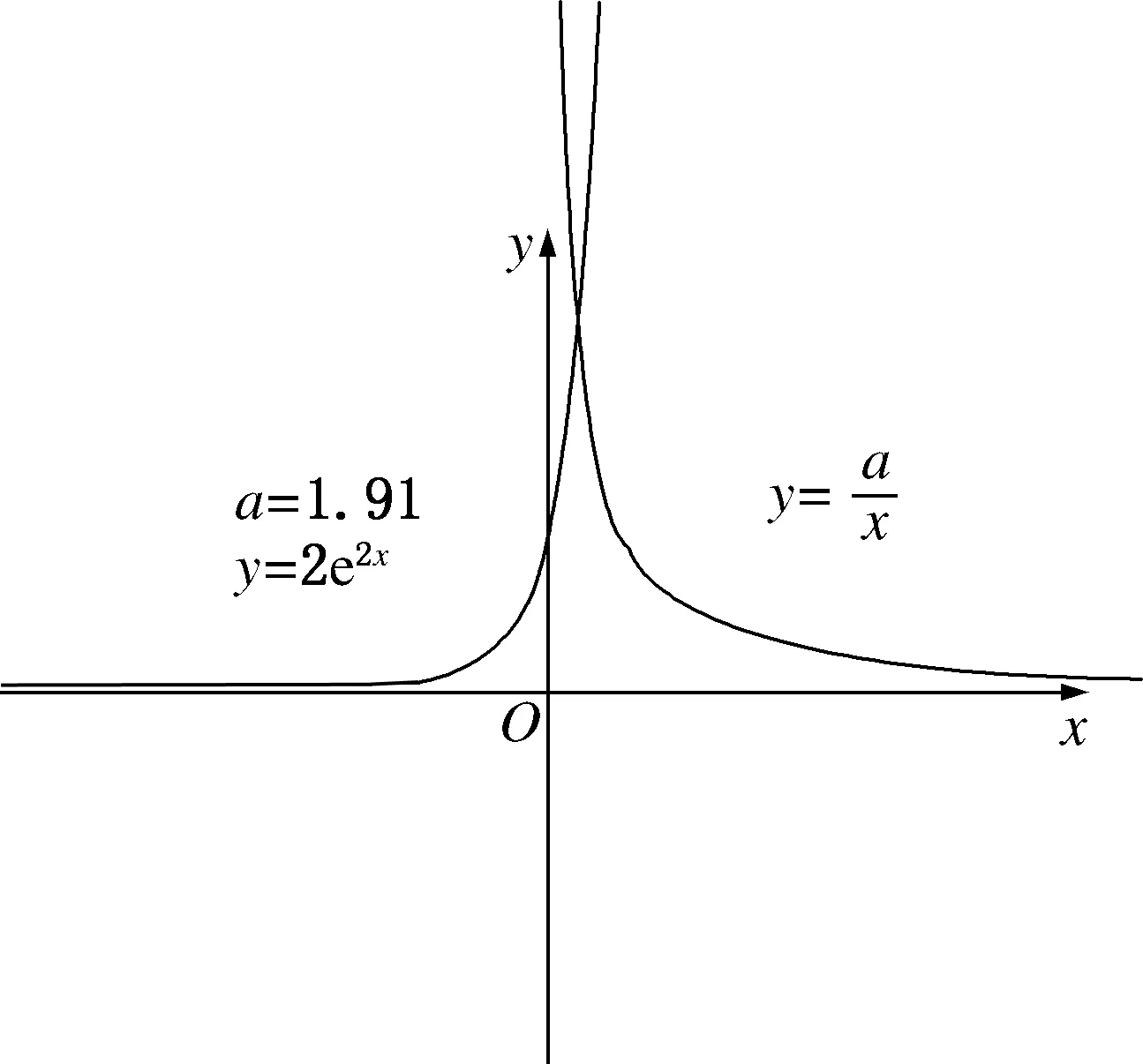
图3
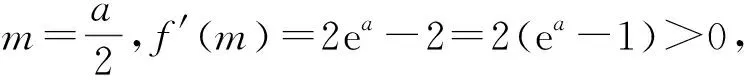
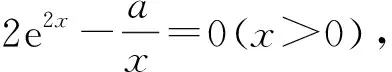
方程①的解也可以看作是g(x)=2xe2x-a在[0,+∞)上的零点(扩大定义域),而当x≥0时,注意到g′(x)=2(2x+1)e2x>0,所以g(x)在[0,+∞)单调递增,g(0)=-a<0,g(a)=2ae2a-a>2a-a>0,所以g(x)=2xe2x-a在[0,+∞)上有唯一零点,问题得到解决.在这个过程中化归思想起了很大的用处,原本函数的端点无法代入,从而无法确定符号,将函数延拓为g(x)=2xe2x-a,使这个问题得到圆满解决.
教学启示:对于“取点”的策略,除了借助不等式放缩以外,还可以归纳得出以下两种方法.
方法1:把含参项消去变为常数项,如上面分析取x=a.
方法2:想要说明存在x0使f(x0)-h(x0)<0,可借助中间量α,说明f(x0)<α,h(x0)>α即可.
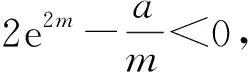
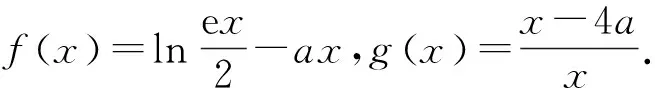
(1)略.(2)当a>0时,函数h(x)=f(x)-g(x)恰有三个不同的零点,求实数a的取值范围.
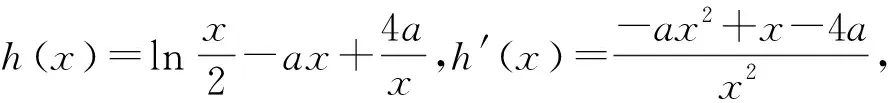
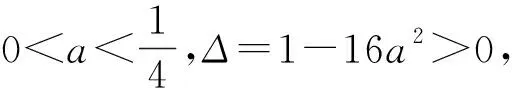
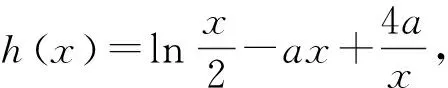

图4
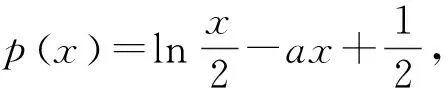
当找到x0∈(2,+∞)使得h(x0)=0后,并不需要在(0,x1)找另一个零点,原因是该零点与x0有特殊的数量关系,往往在对数函数、反比例函数、正比例函数三者叠加的函数中零点会存在这样的关系.
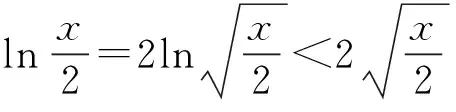
“取点”的过程是一个不断试错的过程,学生需要经历观察、猜想、计算、证明等思维活动,这些过程能发展学生的数学运算、逻辑推理能力.在教学中,教师要教会学生从数学的本质出发,追求通性通法,有效的解题是有专注的选择和有进展的试错.教师也可以在日常教学过程中强化学生对常见函数增长趋势的认识,让学生走向更高的层次.
