基于永磁环阵列的磁流体支撑及润滑特性研究

李晶冰, 戴庆文, 黄 巍, 王晓雷

(南京航空航天大学 直升机传动技术重点实验室, 江苏 南京 210016)

在各种机械结构中，部件之间的摩擦与磨损普遍存在. 这不仅会造成能量损耗，也将不同程度地降低机械可靠性与寿命. 实现低摩擦是人类追求不懈的目标. 近年来，研究人员已从减摩材料、表面设计及涂层等几个方面着手，进行了大量的研究并取得了显著的成效. 随着分子摩擦学的兴起，科学家已从理论上论证了超滑状态(Superlubricity)存在的可能性，由此推开了“零摩擦”的大门[1-2]. 经过多年的发展，超滑研究在理论[3-5]和试验方面[6-8]均取得了长足进步，且已发现了某些具有超滑特性的材料，如富勒烯碳膜[9-10]和石墨[11-12]等，其摩擦系数在10-3量级或更低[9,11]，但上述结果大多是基于点接触，也易受环境因素的影响，暂无法实现工业应用[12-14].

生产实践中最接近超滑状态的是流体润滑状态[15-16]，且理论上无磨损，对于滑动摩擦而言是十分理想的润滑状态. 一般来说，流体润滑可分成流体静压润滑和流体动压润滑，但不论是传统的流体静压或动压润滑方式，均有相应的形成条件. 流体静压润滑需利用泵产生油压，占用空间大；而动压润滑则要借助摩擦副间的相对运动使油膜内压升高产生承载能力，且运动表面间需形成楔形间隙. 如何在摩擦副间实现低摩擦及零磨损特性的同时，又可使油膜在低速或完全静止的平面间依然能产生支撑和承载能力是亟待解决的问题.

磁流体(Magnetic fluid，下文简称MF)的出现为实现上述设想提供了可能，磁流体是将表面包覆有活性剂的纳米级磁性颗粒分散于基载液中形成的稳定固-液两相超顺磁性的胶状液体[17]. 在无外磁场时，磁流体表现出牛顿流体的性质；在外磁场中，磁流体黏度会因其被磁化而升高，从而由自由流动的液体转变为半固体状态[18]，与此同时，该液体还可以被控制并限定于磁场强度较大的位置. 这为构建低速条件下的液体支撑润滑，继而实现低摩擦和零磨损开辟了全新的思路.

作者所在课题组前期研究表明，外磁场作用下的磁流体其液膜支撑能力和润滑性能相比于基载液均有所提升[19]. 王等[20]发现，若磁场由轴向充磁的永磁环提供时，当永磁环底部与基板连接，则上端面吸附的磁流体除了能提供液体支撑外，被磁流体密封在磁环内的气体也可有效提供气体支撑，其原理如图1所示. 该结构所能提供的总支撑力(F)由密封气体产生的支撑力(FG)及磁流体磁化所产生的液体支撑力(FL)两部分组成.

伴随着技术的进步，器件的小型化趋势日益凸显，上述大尺寸单环的磁流体支撑润滑结构在工程应用方面显然存在一定缺陷. 在此基础上，本文作者提出在运动副表面布置环形微小磁体阵列的设想，通过磁体吸附磁流体形成封闭气腔结构，以实现对目标区域的精准支撑与润滑，缓减精密和低速机构中的黏滑行为，同时运动副表面所布置的微小磁体既未改变机构的原有结构，又节省了产生磁场所需的空间.

Fig. 1 Schematic diagram of the liquid-gas support based on magnetic fluid seal图1 磁流体密封空气腔结构的支撑示意图

1 试验部分

1.1 试样材料及制备

选用树脂材料为基底，在其表面嵌入正方形点阵排布的永磁环阵列(N35型NdFeB永磁体，Φ5 mm×2 mm×1 mm，磁性能列于表1中)，形成周期性的磁场分布后，将表面打磨至表面粗糙度Ra小于100 nm，并依次用无水乙醇和丙酮对试样表面进行清洗. 分别在各磁体表面注入磁流体(0.05 mL，磁流体性能参数见表2)，使其在各永磁环表面形成封闭的液体结构(磁流体液体环尺寸约为Φ7.5 mm×1.9 mm×1 mm，形状如图2所示).试样表面永磁环中心距及磁极排布方式列于表3中.

表1 N35型NdFeB永磁环性能参数Table 1 N35 NdFeB permanent magnet ring performance parameter

表2 磁流体物理性质Table 2 Physical properties of magnetic fluid

表3 磁环中心距及磁极排布Table 3 Magnet array spacing and arrangement

1.2 试验方法

本文中的支撑力测试平台如图3所示，测力计压头下移，测量并记录支撑力，其量程及分辨率分别为5 N和0.001 N，测头下压速度为0.01 mm/s. 摩擦试验采用往复式摩擦磨损试验机(日本Sinto Scientific)进行测试，摩擦对偶材质为玻璃. 测试负载取决于支撑试验，往复速度为0.1 mm/s. 每次试验前对设备进行清洁与复位，重新注入磁流体，以确保测试试验初始条件相同.

Fig. 2 Schematic diagram of micro magnet arrays for magnetic fluid support and lubrication图2 用于磁流体液-气混合支撑润滑的磁体阵列示意图

2 结果和讨论

图4为单个永磁环(N35型NdFeB，Φ5 mm×2 mm×1 mm)吸附磁流体后的支撑力测试曲线，可以看出，随着压头下移，支撑力逐渐增大. 对于底部开放的永磁环试样，其支撑能力(F)仅来自磁流体的液体静磁力(FL)，就磁流体而言，其内部每个磁性颗粒的磁偶极矩在无外磁场条件下随机取向，但在外磁场作用下，颗粒的磁矩将沿外场取向，对外显示宏观磁化强度. 从理论上讲，磁流体所能提供的液体支撑力与其磁化强度和所施加磁场的梯度之积成正比[21]. 随着压头的下移，支撑间隙逐渐减小，相应的磁场强度及梯度均逐步增加，液体的静磁力随之提高.

对于底部密封的永磁环试样，在同等条件下，由于被磁流体密封在磁环内部气体的参与(FG)，其所提供的支撑力较底部开放试样的更大. 当支撑间隙h为0.01 mm时，底部密封试样的最大支撑力约为0.061 N，约为底部开放试样支撑力(约0.038 N)的1.63倍. 其具体的密封气体支撑原理如图1所示，根据磁流体密封原理，其液环内外侧的压差[22]可表示为式(1)：

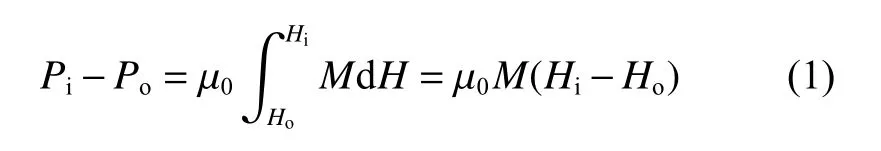
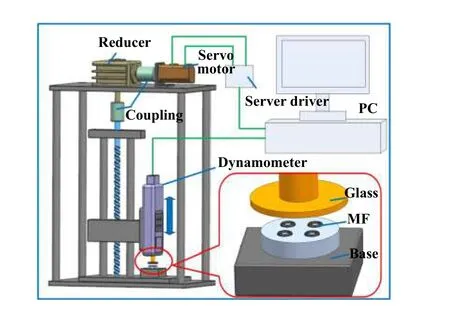
Fig. 3 Schematic diagram of support test system图3 支撑力测试系统示意图

Fig. 4 Curve of supporting force of a single ring magnet图4 单个永磁环支撑力测试曲线图

其中：Pi和Po分别是在磁流体的内部和外部边界处的气体压强，而Hi和Ho分别是磁流体内界面和外界面的磁场强度，μ0为真空磁导率，M为磁流体的磁化强度，其值是外磁场的函数. 由于密封间隙中的磁场强度高达105A/m，磁流体可以视为饱和状态(Ms)[23]. 气体支撑力(FG)可通过对支撑区域面积(AF=πri2n)的压力积分获得：

可以看出，腔室内气体产生的支撑力主要依赖于磁流体的密封能力，如图1所示，压头的下移会导致磁流体液-气界面的位置及其对应的磁场强度发生改变，使得内外界面磁场强度差值逐渐增大，进而提升气体支撑力. 研究过程中，对压头在不同间隙高度时的气体支撑力进行了理论计算，结果如图4所示. 这里以液膜高度0.01 mm位置处的支撑力为例，采用Ansoft Maxwell ver. 16.0软件分析获得此时磁流体环内外界面对应的磁场强度分别为Hi=5.6×105A/m和Ho=5.2×104A/m；μ0为真空磁导率，值为4π×10-7N/A2；Ms为2.4×104A/m；AF为空气腔面积，其值为5.7×10-8m2；根据公式(2)可计算得出FG的值为0.022 N.

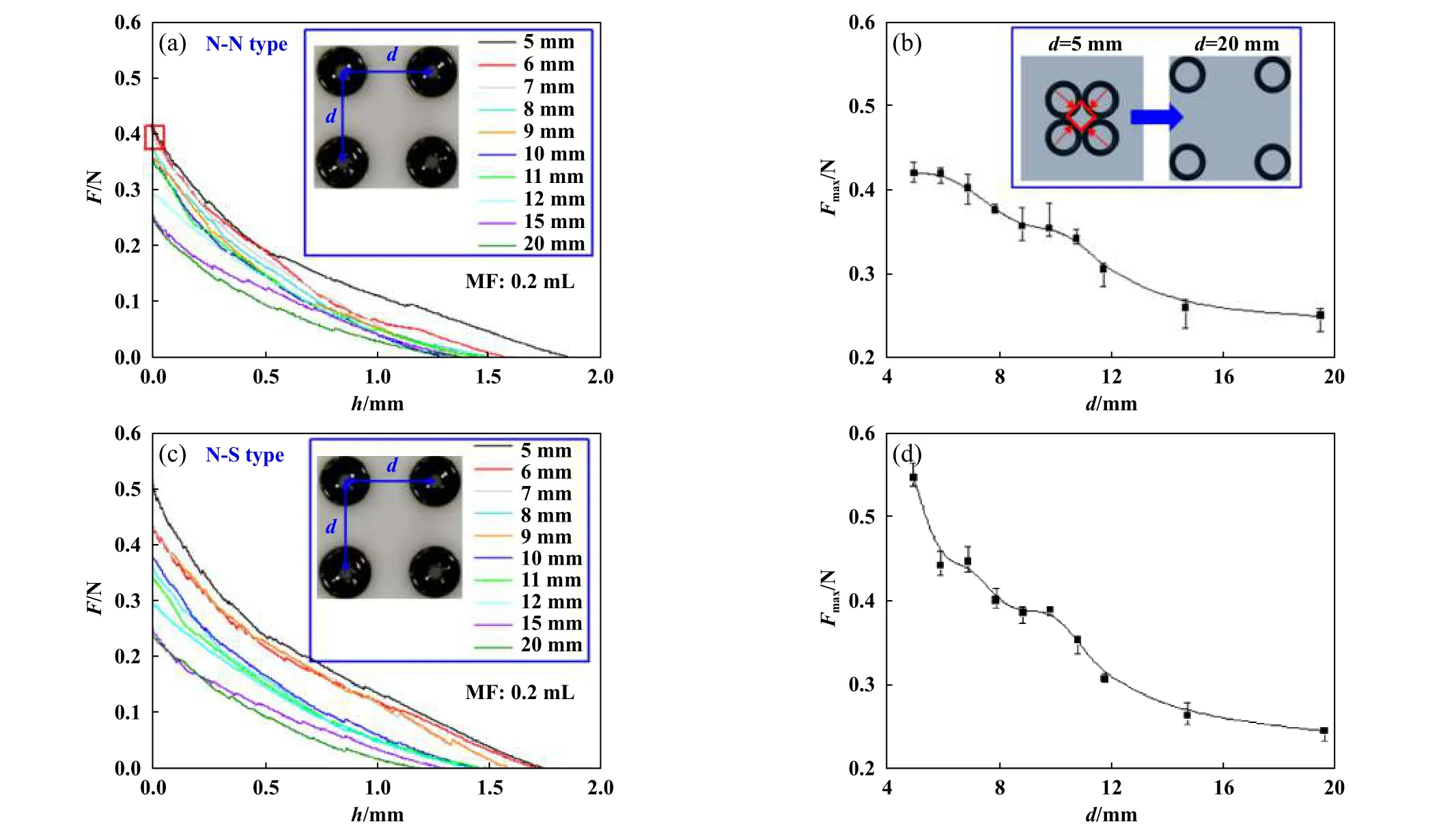
Fig. 5 Effects of space and pole arrangement on the supporting force: (a) (c) original curve of support force with different spacing under N-N and N-S arrangement; (b) (d) diagram of the maximum support force with differentspacing under N-N and N-S arrangement图5 磁环阵列不同间距和磁极排布方式对支撑力的影响：(a) (c)N-N与N-S排布下的不同间距的支撑力原始曲线图；(b)(d)N-N与N-S排布下的不同间距的最大支撑力图

图5所示为永磁环阵列在不同间距及磁极排布方式下的支撑力测试曲线图，可以看出，随着压头下移，各试样的支撑力逐渐增大. 由图5(a)可以看出，当永磁环阵列呈同级N-N排布时，中心距为5 mm的阵列所提供的支撑力最大，约为0.42 N；间距为20 mm时支撑力最小，仅为0.23 N，前者几乎为后者的两倍. 而图5(b)是N-N排列的阵列试样的最大支撑力随间距变化曲线图，由图可见，随着永磁环间距的增大，其支撑力逐渐减小. 这是因为当间距较小时，除了4个磁环阵列试样本身形成液-气混合支撑外，四磁环边界接触部分形成了1个额外的气腔[见图5(b)中红色线框]，会产生附加支撑能力，但随着间距的增大，试样中部的气腔逐渐消失，这种额外的支撑能力逐渐减弱，则总支撑力逐渐减小. 而图5(c)表明，当永磁环阵列呈N-S排布时，中心距为5 mm的永磁环阵列所提供的支撑力约为0.54 N；间距为20 mm时支撑力约为0.25 N. 相比NN排布的永磁环阵列，N-S排布的阵列试样在中心距较小时(d=5～10 mm)的支撑力有一定程度的提高，但随着间距的增大(d=11～20 mm)，这两种磁极排布方式所呈现的支撑力相近.

为了进一步解释这种现象，文中采用Ansoft Maxwell 3D软件分别计算了各试样表面的磁场分布情况，部分结果如图6所示. 从图6中可以看出，磁场最强的位置均集中在磁环边缘，随着永磁环中心距的增加，各环磁场互相之间的影响减弱；当中心距增大到一定程度时，磁场基本无影响，阵列中每个磁环将各自实现承载. 当永磁环中心距为5 mm时，磁极同向排布的N-N型试样[图6(a)]由于同极相斥的缘故，磁环接触位置的磁场强度较低；而对于N-S型排布形式[图6(d)]，磁环单元由于异极相吸的原因，在磁环接触处的磁场强度急速升高，进而使其支撑与密封能力均有所提高，宏观上表现出更高的承载能力.

图7为四永磁环阵列的单环效率比曲线图，该曲线是将永磁环阵列所实现的支撑力平均分摊到单个磁环上，再与图4中底部密封磁环的支撑力进行比较所得. 由图7可见，随着间距的增大，单环效率比逐渐降低. 当间距较大时(大于15 mm)，永磁环阵列中的单个磁环效率比约为1，说明此时各磁环独立实现承载；随着间距减小，单环效率比逐渐提高，说明此时阵列的承载能力不仅只是单环的4倍，还有额外的增值效应，且间距越小，增值效应越明显. 当间距为5 mm时，单环效率约为1.7左右. 与此同时，改变永磁环阵列的磁极排布可进一步的提升阵列单环的增值效率，当间距为5 mm时，磁极N-S排布方式的效率比约为2.2，相比N-N排布方式，效率又进一步提升.

Fig. 6 3D visualization of partial magnetic field distribution图6 部分试样表面磁场分布

Fig. 7 Efficiency ratio curve of single ring in permanent magnet ring array图7 永磁环阵列单环效率比曲线图

图8为部分永磁环阵列试样在0.4 N载荷下的摩擦系数曲线图，该试验载荷皆由支撑试验结果选定[见图5(a)]. 三种N-N排布试样的试验结果如图8(a)所示，大间距试样(No.10，d=20 mm)摩擦系数最高，约为0.036；小间距试样(No.1，d=5 mm)摩擦系数较低，约为0.005；中间距试样(No.6，d=10 mm)摩擦系数介于二者之间，约为0.022. 由支撑力测试结果可知，摩擦过程中所施加的载荷(0.4 N)可由小间距试样No.1的支撑力完全承载(约0.42 N)，但该值略高于试样No.6的承载极限(约0.35 N)，而远大于试样No.10的承载能力(约0.25 N).因此可以推断，对于试样No.1，其上下摩擦副之间完全被液-气分离，从而实现低摩擦. 同时因为磁流体在磁场中被吸附定位的原因，其他间距试样虽无法完全承载，但接触面也存在一定的磁流体，故摩擦系数总体较低，摩擦副处于混合润滑状态.

图8(b)中三种N-S排布试样的摩擦试验结果与N-N排布试样的趋势相似，这一结果表明，只要负载小于磁流体密封腔结构的承载能力，该负载将会被磁流体与其形成的密封空气腔完全承载，实现运动副之间的完全分离，从而获得优异的润滑效果. 与经典的流体动压或静压润滑不同，这种磁流体轴承结构不依赖相对运动或泵，且在静止状态下依然能够提供承载力.

3 结论

以树脂材料为基底，在其表面嵌入正方形点阵排布的永磁环阵列，形成周期性的磁场分布. 分别在各磁体表面注入特定体积的磁流体，使其在磁环表面形成封闭的液体结构，随后对各试样进行了支撑力及润滑试验，根据试验结果，得出以下结论：

Fig. 8 Friction curves of some magnetic array samples图8 部分磁性阵列试样的摩擦曲线

a. 底部密封的单个永磁环试样与底部开放的试样相比，可以产生更高的支撑力(约0.061 N)，更为重要的是，该液-气混合支撑力不依赖于外部的泵或相对运动，即使在静止状态下也依然存在.

b. 正方形点阵排布的永磁环阵列的支撑力随着阵列间距的减小而增大，且在一定间距范围内，磁环的磁极排布也会对支撑力产生影响，相比N-N排布，N-S排布方式产生的支撑力更高.

c. 当永磁环阵列的承载能力大于所加载荷时，该支撑结构可获得0.005的低摩擦系数.