泛系拓扑与粗糙集
2022-07-08王晓艳马骥
王晓艳 马骥
(1.山西工程科技职业大学 山西省晋中市 030619)
(2.中国能源建设集团山西省电力勘测设计院有限公司 山西省太原市 030000)
1 引言
1.1 经典粗糙集理论的基本概念
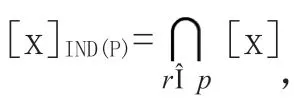
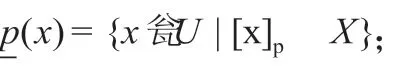
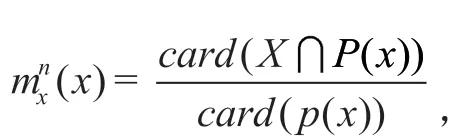
可见,给定知识库K(U,R),对于每个子集X U和一个等价关系R∈ind(K),可以根据R的基本集合的描述来划分集合X。为了衡量{des(Yi): Yi∈R}精确地说明X中对象的隶属情况,考虑两个子集:
R_(X)=∪{Y∈U/R:Y X}
R—(X)=∪{Y∈U/R:Y∩X≠∅}
分别称它们为X的R下近似集和R下近似集。集合bnR(X)= R—(X)-R_(X)称为X的R边界。
通常把posR(X)=R_(X)称为X的正域,把negR(X)=R—(X)称为X的R负域,把bnR(X)称为X的边界域。
正域posR(X)或X的下近似是那些对于知识R能完全确定地归入集合X的对象的集合。类似地,negR(X)是那些对于知识R毫无疑问不属于集合X的元素的集合,它们是属于X的补集。边界域是某种意义上论域的不确定域,对于知识R属于边界域的对象不能确定地划分是属于X或是-X。X的上近似是由那些对于知识R不能排除它们属于X的可能性的对象构成的,从形式上看,上近似就是正域和边界域的并集。
关于粗糙集理论的详细描述请参见文献。
1.2 泛系理论
泛系理论是研究广义系统的学科。广义系统可看成广义硬件与广义软件的复合体或软硬兼设体,这里广义硬件可以是任何事物集,包括是另外的广义系统或广义软件集,而广义软件则是有关的某些关系或带参量的关系以及它们的迭代生成。形式上,可以定义广义系统:((广义硬件,广义软件))。广义硬件:(任何事物集;任何广义系统集;任何广义软件集);广义软件:(广义硬件与参量的泛权关系族;广义硬件与参量的泛系关系族;广义软件*广义软件)。系统观是一切研究的基础,粗集理论首先是以知识库(近似空间)为研究基础的,知识库(近似空间)就是一个关系系统。
2 粗糙集近似的拓扑结构
2.1 泛系拓扑
为了规范化地研究极限和极限过程,数学家引入了拓扑空间的概念,它是泛系论中一种特殊的广义系统:S=(A,B),B⊂P(A),B叫做拓扑空间S或者A的拓扑结构,实际上是A的一子集族,但是要加入一些规定(四条公理),B的元素(A的子集合)就叫做邻域,任何A元素x,yÎbÎB,则称x,y是按照b意义下近邻的,而对于任何广义的点(元素)x,假如存在bÎB使得xÎb,则称x为拓扑空间S的内点,所有内点的总和就形成拓扑空间S的内域。A中的子集合假如都是内点,则叫做开集合。假如C⊂A,xÎA,不一定属于C,对于任何给定的bÎB,xÎb,则必然存在C的点yÎC,使得y也属于b,yÎb,这时候就叫做x是C的凝聚点。自然也是C的极限。当x同时是C和C的补集合的凝聚点的时候,就叫做C的边界点。这里可以自然地看到,林林总总的bÎB 就是许多泛极,是许多广义的零,是广义的零距离,同时它们也是许多泛系论下的泛系尺度,它们是用测量广义的远近的,是泛系量化(相对地辨异同,排泛序)的手段。而且,有趣的是,这些泛极,这些泛系尺度本身又是相互有泛系量化关系的,即可以再相对地辨异同,排泛序,自然也可以显运转(b是集合,它们可以相对地进行广义的四则运算/加减乘除),这里泛极成为泛系尺度,泛系尺度是泛系量化的工具,泛系尺度族又可以再进行泛系量化。而现代拓扑学就是用B这一组“泛极/泛系尺度/广义的尺子/广义的先验的知识库”来建构或者研究各种iceb——内外、边界、运转、连续性、连通性、拓扑变换、拓扑泛对称等等。这样现代拓扑学的理法又可以和泛系相对论联系起来,也成为泛系相对论论述相对性的有力工具。
定义3:串并空间:对于论域U上给定的某些泛权关系族{fi}经过广义的串行(复合*)与并行(关系的并∪与交∩)反复运算生成的类,记为,它指出:(1)fiÎSp(fi),ÆÎSp(fi),UÎSp(fi);(2)若g,gÎSp(fi),则g*g,g∪g,g∩gÎSp(fi)。其中,由广义的串行(复合*)反复运算生成的类为串空间;由广义的并行(关系的并∪,交∩)反复运算生成的类为并空间。
定义4:泛系拓扑:假使S=(A,B),BÍA2是一泛系系统,HÍA,xÎA:
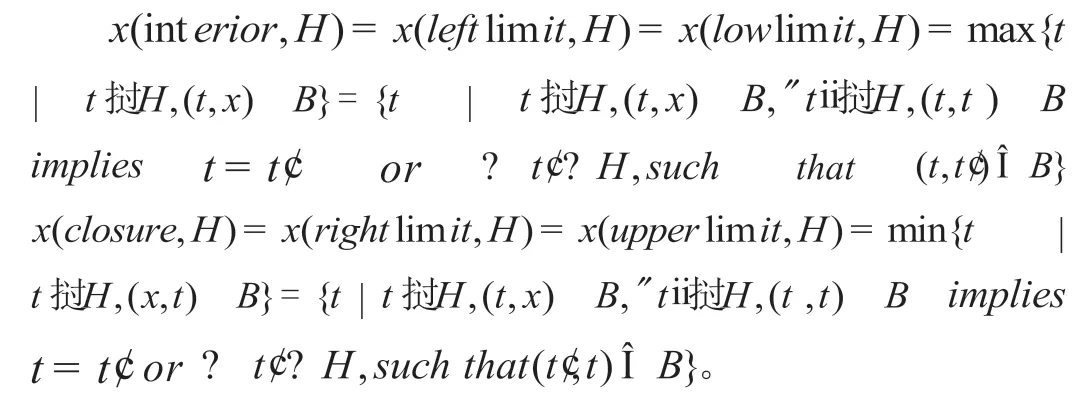
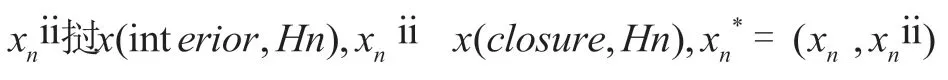
2.2 基于泛系拓扑的粗集近似
定义5:基于泛系拓扑(定义4),对于S=(A,B),我们约定A为论域U的幂集,记为p(U),B为A上的偏序关系(一般为包含关系),则S构成U的幂集上的格,记为S=
下面举实例加以说明:
例1:论域U={1,2,3,4},则p(U)={{1,2,3,4},{1,2,3}, {1,2,4},{1,3,4},{2,3,4},{1,2},{1,3},{1,4},{2,3},{2,4},{3,4},{1},{2},{3},{4},∅},下图(图1)为泛系拓扑S=
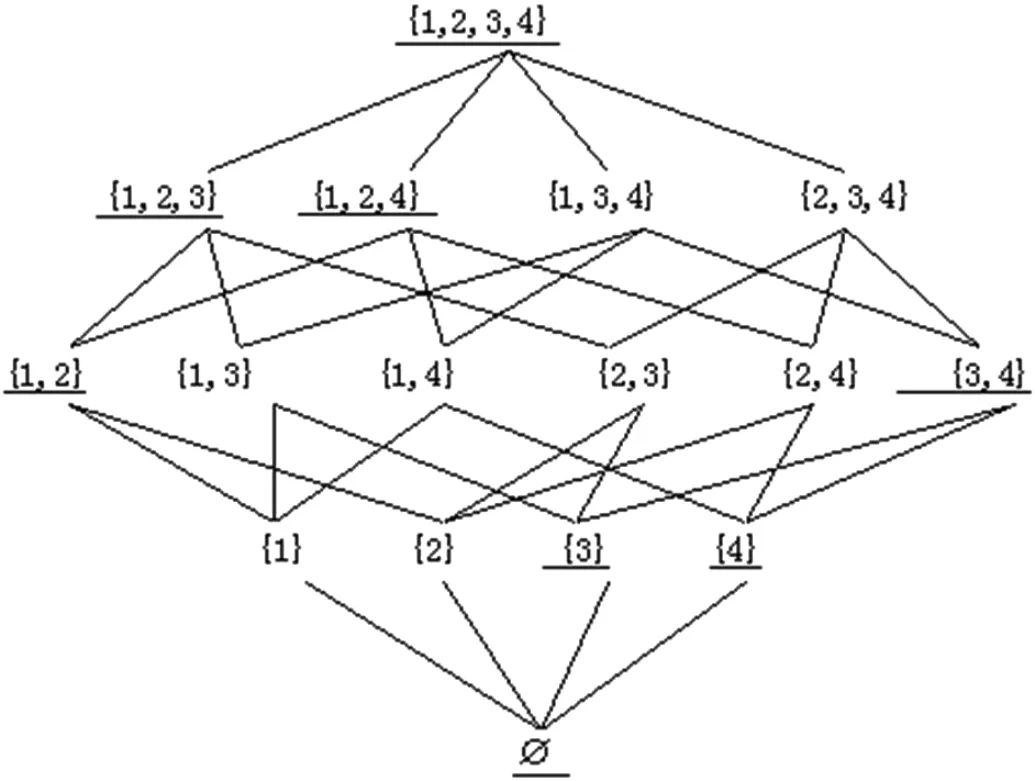
图1:泛系拓扑S
若讨论集合x={1,3},基于定义5,我们可以从上图2.2.1的并空间H中一眼得出集合x的上下近似分别为{1,2,3}和{3}。
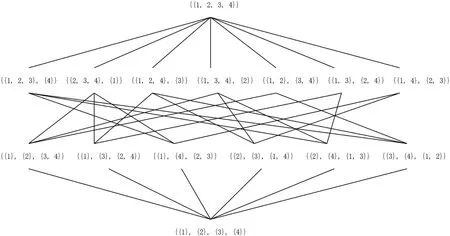
图2:泛系拓扑S3
若讨论集合x={1,2},基于定义5,{1,2}本身即为集合x的上下近似。
实质上,上近似和下近似分别体现了泛系拓扑结构中的上逼近(右逼近、外逼近)和下逼近(左逼近、内逼近),也就是说,粗集近似的本质也属于一种逼近,那么,将它与泛系逼近转化论联系起来将是一个新的方向。
2.3 基于泛系拓扑的决策表属性约简
定义6:K=(U,A)为一知识表达系统,且C,D A是两个属性子集,分别称为条件属性,且C∪D=A,C∩D=∅具有条件属性和决策属性的知识表达系统可表达为决策表,记做T=(U,A,C,D)。关系ind(C)和关系ind(D)的等价类分别称为条件类和决策类。当且仅当C D(即ind(C) ind(D)),决策表T=(U,A,C,D)是相容的。
我们都知道,粗糙集的属性约简从系统观来看是系统间的问题。在此基于泛系拓扑,可以把属性约简问题转化为一个系统内的问题。集合的包含关系能够推导出集合的细分关系。给定集合U,那么U上的所有等价关系就决定了U上的一组划分,同时U上的所有等价关系就组成了泛系拓扑,可以表示为(P (U), Δ),其中“P (U)”表示U上的一组划分,“Δ”表示细分关系。在泛系拓扑(P (U), Δ)中,来讨论粗糙集中决策表的相容性及属性约简,由于(P (U), Δ)是一个系统, 所以基于泛系拓扑讨论粗糙集中决策表的相容性及属性约简,在此就是一个系统内的问题了,而不是系统间的问题。泛系拓扑实质上就是泛系中广义系统的一种体现。
广义系统可以形式地递归定义为广义系统:((广义硬件,广义软件)),广义硬件:(任何事物集;任何广义系统集;任何泛系集),广义软件:(广义硬件的泛权关系族;泛系硬件的泛权泛系关系族;广义软件的复合)。各种数学结构,各种系统概念均可用广义系统来描述。一种泛系一元观也认为万事万物、百科千题均自成广义系统又互成广义系统。广义系统的概念比流行的一般系统的概念在哲理普适性、数理确切性与简明性及便于研究方面,以及在技理具体性方面均更突出而具有融哲理、数理与技理于一体的一体性,它也是一种广义的量,是广义量化的工具。泛系理论(泛系哲学、泛系数学、泛系工学)已把许多百科理法显生为系统科学在哲理、数理与技理三种层次上提供新的建树。
下面我们举例加以说明。
例:给定U= {1, 2, 3, 4},条件属性表是一个系统,如S1= (U, C),决策属性表是另一个系统,如S2= (U, D),所以,粗糙集的属性约简是一个系统间的问题。下面将其转换为一个系统内的问题来讨论,这个系统就是泛系拓扑S3,S3= (P (U), Δ)。
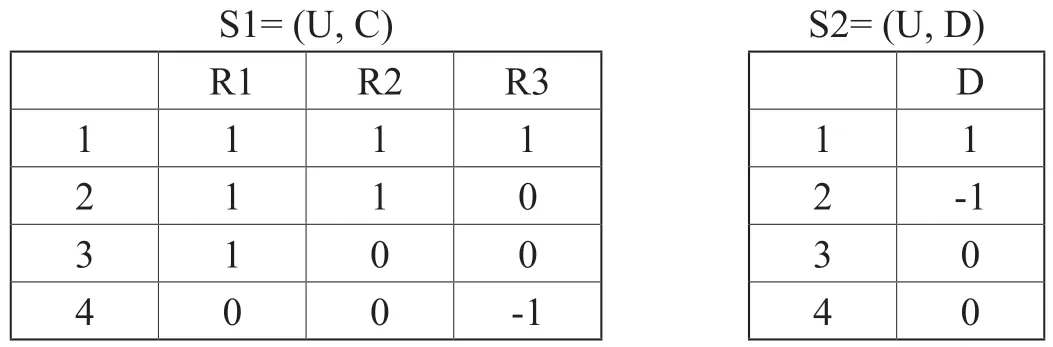
S1= (U, C) S2= (U, D)R1 R2 R3 1 1 1 1 2 1 1 0 3 1 0 0 4 0 0 -1 D 1 1 2 -1 3 0 4 0
这里,U上所有等价关系决定的一组划分如下:{{1, 2, 3, 4}}, {{1, 2, 3}, {4}}, {{2, 3, 4}, {1}}, {{1, 2, 4}, {3}}, {{1, 3, 4}, {2}}, {{1, 2}, {3, 4}}, {{1, 3}, {2, 4}}, {{1, 4}, {2, 3}}, {{1}, {2}, {3, 4}}, {{1}, {3}, {2, 4}}, {{1}, {4}, {2, 3}}, {{2}, {3}, {1, 4}}, {{2}, {4}, {1, 3}}, {{3}, {4}, {1, 2}}, {{1}, {2}, {3}, {4}}。由此组成的泛系拓扑S3= (P (U), Δ)如下:
如图2所示,从S3中,可以得到一些规则:
定义7:基于定义4,设A=P (U), B A是一细分关系,即S=(P (U), Δ),其中条件类,条件类的交集,决策类分别是S=(P (U), Δ)中的元素,由定义3,H就是一个由条件类、条件类的交集组成的并空间,显然(H, Δ)是S=(P(U), Δ)的子拓扑。假定x∈P(U)是决策类,如果min(H)△x or min(H)=x (min(H)={t | , , such that }),即min(H)) x,由定义6,决策表是相容的,否则是不相容的。且构成值为min(H)的条件类的最小集合,即为该决策表的约简。
下面举实例加以说明:
例2:已知论域U={1, 2, 3, 4},条件类分别为:U/R1={{1, 2, 3}, {4}},U/R2={{1, 2}, {3, 4}},U/R3={{1}, {4}, {2, 3}},决策类为 U/D= {{1}, {2}, {3, 4}},则:
U/R=U/ {R1, R2, R3} = {{1}, {2}, {3}, {4}}
pos(D)= {1, 2, 3, 4}
U/ {R1, R2} = {{3}, {4}, {1, 2}} pos(D) = {3, 4}
U/ {R1, R3} = {{1}, {4}, {2, 3}} pos(D) = {1, 4}
U/ {R2, R3} = {{1}, {2}, {3}, {4}} pos(D) = {1, 2, 3, 4}
所以属性R2和R3是D不可缺少的,所以约简为{R2, R3} ,也是核。
例2的泛系拓扑S=(P (U), Δ)如图3所示。
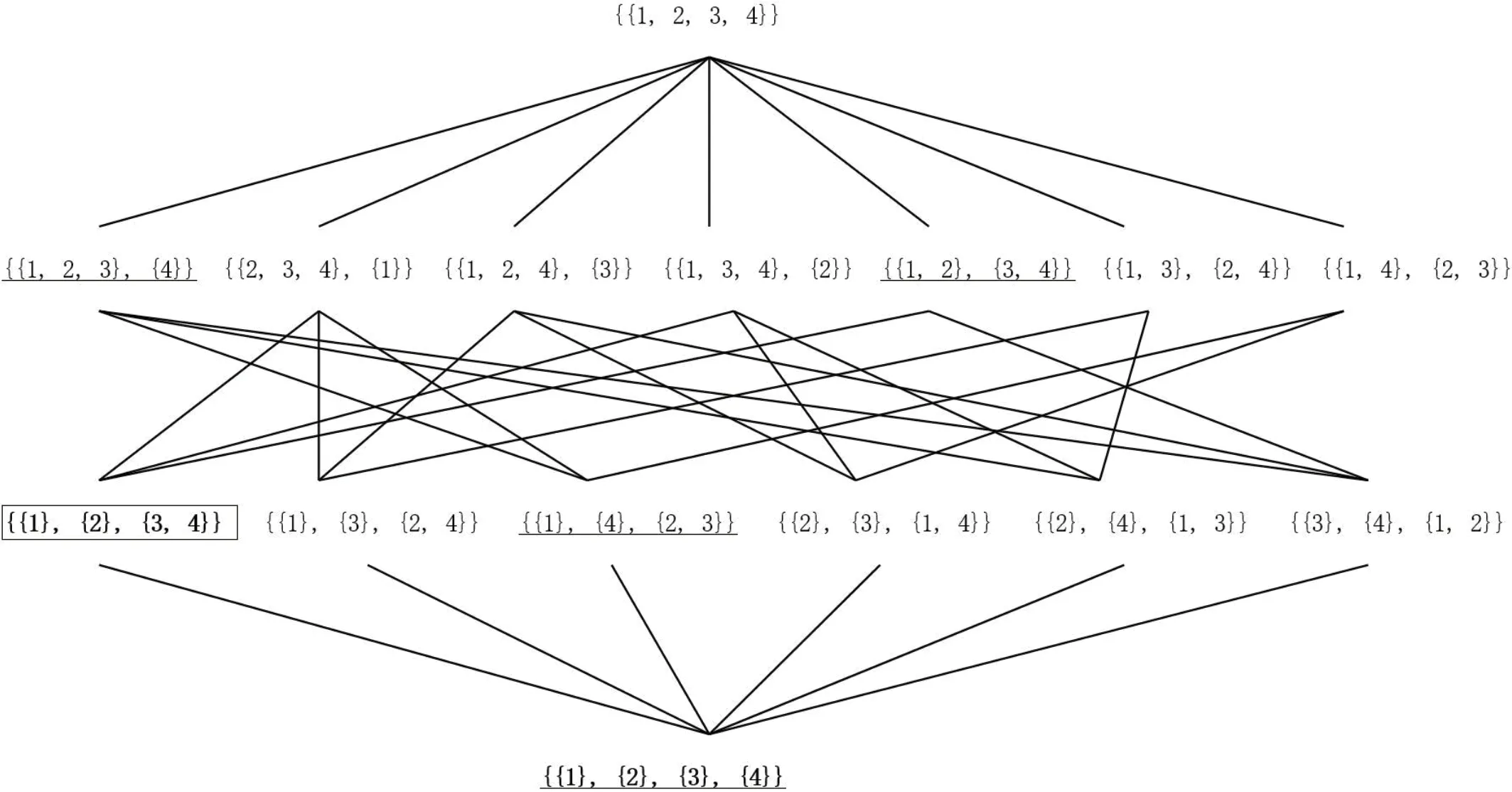
图3:泛系拓扑S
由定义7,加下划线部分为并空间 H(由条件类,条件类的交集组成),加方框部分为决策类x={{1}, {2}, {3, 4}},min(H) = {{1}, {2}, {3}, {4}}, 由于min(H)△x,所以该决策表是相容的,而且min(H)= U/{R1, R2, R3} 或 U/{R2, R3},显然最小集合为{R2, R3},所以{R2, R3}是决策表的约简。
3 结论
本文将粗糙集与泛系拓扑、串并空间联系起来,从本质上刻画粗糙集的一些概念,并加以扩展,得出粗糙集近似就是串并空间下,上逼近(右逼近、外逼近)和下逼近(左逼近、内逼近)的体现;同时从泛系拓扑的角度,结合泛系逼近转化论等理论研究决策表的相容性与属性约简问题,将系统间的问题转化为系统内的问题来讨论,得出相应的结论。
