基于边界约束的煤矿井下尘雾图像去雾算法

曹虎晨， 姚善化， 王仲根

（安徽理工大学 电气与信息工程学院，安徽 淮南 232001）

0 引言

采煤机在采煤过程中会有大量的尘雾产生，这些弥漫在空气中的尘雾不仅会影响煤矿工人的身体健康，还会造成井下事故的发生。通常在煤尘中注水[1]或在采煤机处喷洒大量的水雾[2]，以达到降尘的目的，但水雾严重影响采集到的图像质量，不利于后续对目标的识别和跟踪等处理。因此，研究煤矿井下图像去雾具有重要意义。

应用较广泛的图像去雾算法可分为基于图像增强、基于卷积神经网络（Convolutional Neural Networks,CNN）、基于物理模型3类[3]。基于图像增强的去雾算法有Retinex算法、同态滤波等。文献[4]在HSV空间下用改进的双边滤波算法融合多尺度Retinex算法，在色彩和边缘模糊处理等方面有所提升，但是去雾效果不好，易出现过曝光。文献[5]先通过同态滤波提高图像清晰度，再采用直方图均衡化突出边缘信息，提高了图像特征点选取的准确率，该方法通过增强图像对比度等来突出边缘细节，算法简单，但是去雾效果差，易出现过曝光等问题。基于CNN的去雾算法用CNN建立一个端到端的网络，再利用数据集来训练这个网络，从而得到无雾图像。文献[6]提出基于深度融合网络的去雾算法，该算法构建了较大规模的去雾数据集，解决了图像过增强现象。但该方法去雾效果差，且煤矿井下去雾数据集很少，难以训练出一个好的去雾模型。基于物理模型的去雾算法依据大气散射模型对尘雾进行处理。文献[7]通过观察大量户外有雾与无雾图像的差异，提出了基于暗原色先验的图像去雾算法（以下简称He算法）。该算法简单，去雾效果好，但细节处理效果较差，易出现去雾图像过曝光等问题。文献[8]提出一种基于暗原色先验的煤矿井下退化图像复原算法，使用正则化拉普拉斯矩阵构建暗原色先验去雾尘模型，该算法对图像细节处理较好，但是去雾后的图像偏暗，且容易失真。文献[9]基于暗原色理论提出了一种自适应双边滤波的煤矿尘雾图像增强算法，该算法在去噪的同时极大地保留了图像的边缘特征，但对细节处理较差。文献 [10]提出了基于边界约束及上下文正则化的去雾算法（以下简称Meng算法），首先通过限制传递函数的固有边界得到粗透射率，其次通过上下文正则化得到精细化透射率，最后用精细化后的透射率通过大气散射模型来恢复无雾图像，该算法对细节部分除雾效果很好，但容易出现局部透射率估计不准确的问题，且去雾图像会出现颜色失真、对比度过饱和等问题。文献[11]提出了对边界约束进行双边滤波优化的图像去雾算法，将图像分割成天空区域与非天空区域，对天空区域与非天空区域分别处理，解决了图像过曝光的问题，但图像分割需要手动操作，算法处理时间较长。

针对上述问题，本文将He算法与Meng算法进行融合，提出了一种基于边界约束的煤矿井下尘雾图像去雾算法。首先，用伽马校正改变井下图像亮度，选取开运算处理后的图像颜色通道的最大值作为煤矿井下的大气光值。其次，分别用暗通道算法与边界约束算法对图像进行处理，对边界约束算法得到的边界约束图进行引导滤波，得到更为清晰的边界约束图，并将边界约束算法的粗透射率与暗通道先验算法的粗透射率进行比较再融合。最后，经过上下文正则化细化透射率，再通过大气散射模型得到去雾后的图像。

1 相关理论

1.1 大气散射模型

在计算机视觉中，大气散射模型[12]广泛用于图像去雾，即

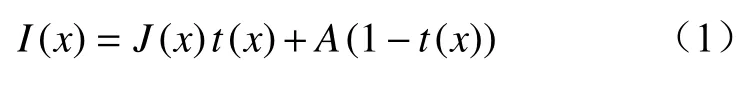
式中：I(x)为有雾图像，x为图像中像素点位置；J(x)为无雾图像；t(x)为透射率；A为全球大气光值。

图像成像中的大气散射光导致了图像的对比度下降和颜色失真等问题。去雾的目的是通过单幅图像来准确估计全球大气光值A和透射率t(x)，从而恢复无雾图像J(x)。

1.2 He算法原理

He算法的暗通道先验知识中提到无雾图像总会存在一个颜色通道的值接近0，故对无雾图像中每个像素的颜色通道值最小化可得到暗通道图像。

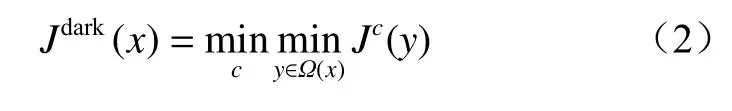
式中：Jdark(x)为暗通道图像；c为红绿蓝三色通道中的某一通道；y为图像中像素点位置；Ω(x)为以x处像素为中心的一个窗口；Jc(y)为像素点位置为y的彩色无雾图像。

将暗通道先验知识与尘雾图像成像模型结合，对式（1）进行2次最小滤波后求解出透射率。假设最小滤波后的透射率没有改变，则透射率为

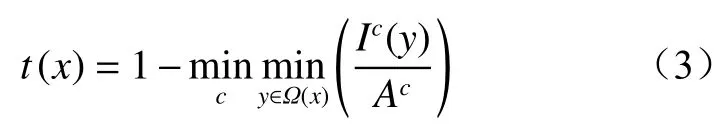
式中：Ic(y)为像素位置为y的彩色有雾图像；Ac为彩色通道的大气光值。

1.3 Meng算法原理

在无雾的情况下，透射率接近1，I(x)≈J(x)。随着雾浓度的增加，t(x)会逐渐减小，I(x)≈A，所以文献[10]提出了一个边界约束理论，即无雾图像的亮度值存在下边界B0与上边界B1，由式（1）可知，当A一定时，t(x)也存在边界tb(x)。

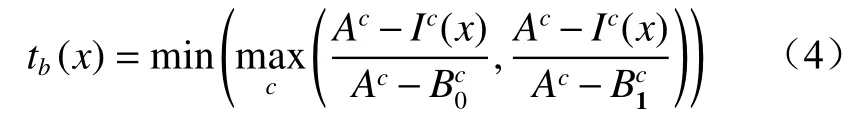
式中：Ic(x)为像素点位置为x的彩色有雾图像；,分别为某一颜色通道的下边界与上边界。

在实际生活中存在边缘区域透射率跳跃的情况，若采用式（4）估计透射率，会导致图像边缘出现伪影效应。为了解决伪影效应问题，引入了权重函数W(x,z)[10]。

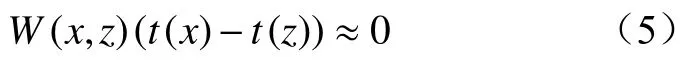
式中z为图像中与x相邻像素点的位置。

当t(x)与t(z)相差很大时，W(x,z)就要很小才能使式（5）成立，反之亦然。依据这个限制，可采取相邻像素亮度差的方式来定义权重函数。

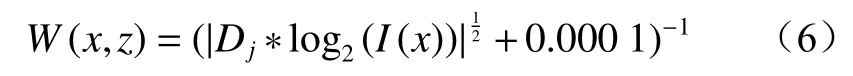
式中：Dj为像素点j的差分滤波算子，由8个Kirsch边缘检测算子与1个Laplacian算子构成；*为卷积符号。

虽然引入权重函数解决了图像边缘伪影的问题，但Meng算法在图像非边缘的区域存在透射率不相似的问题，这不符合最优透射率原则。为了获得最优透射率，引入惩罚项，构建新函数H(x,β)。

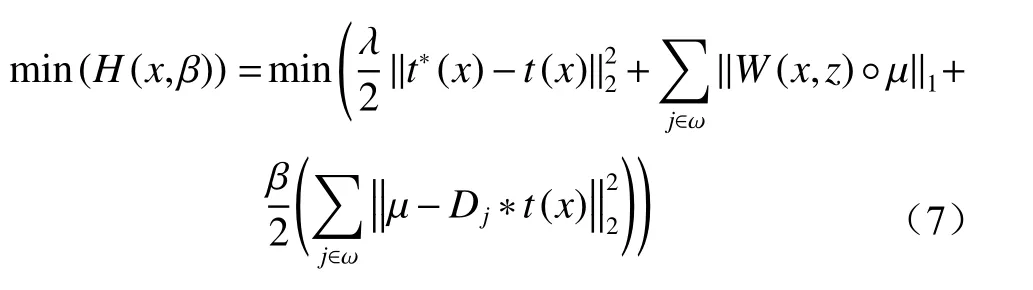
式中：β为惩罚因子；λ为正则化参数；t*(x)为优化后的透射率；°为元素相乘符号；ω为像素索引集；μ为辅助变量。

当透射率满足式（4）的边界约束条件时，H(x,β)的值最小，透射率最优。当不满足约束条件时，H(x,β)的值很大，应舍去，以达到特征稀疏化的目的。

通过交替最小化算法将与μ有关的项分离出来，通过与 μ相关函数的最小值求解出μ。

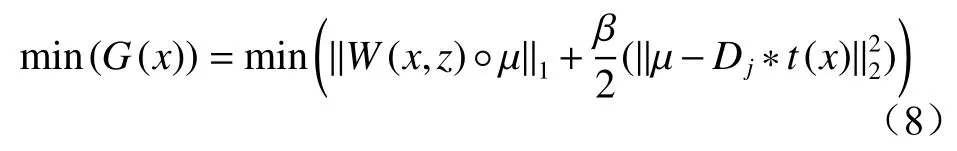
结合式（7），利用二维快速傅里叶变换，并假设圆形边界条件，最后求得t*(x)为

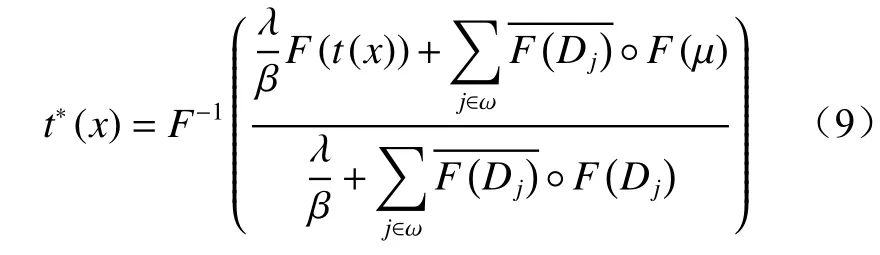
式中：F-1为傅里叶逆变换；F为傅里叶变换；为复共轭变换。

2 本文算法原理

2.1 基于边界约束的煤矿井下尘雾图像去雾算法流程

基于边界约束的煤矿井下尘雾图像去雾算法主要包括大气光值的获取、He算法与Meng算法的粗透射率融合、上下文正则化、图像去雾等。算法流程如图1所示。

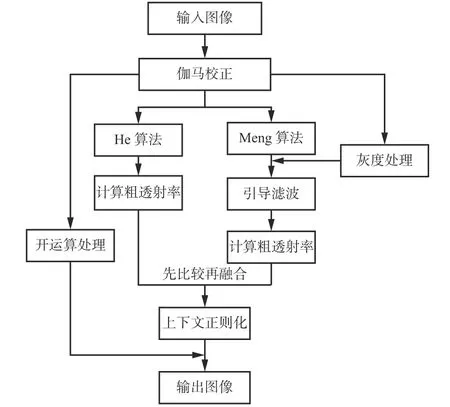
图1 去雾算法流程Fig. 1 Flow chart of defogging algorithm

首先，对输入的图像进行伽马校正，对校正后的图像进行颜色通道开运算处理，从开运算后的图像中选取亮度最大值作为大气光值。其次，分别用He算法与Meng算法对伽马校正后的图像进行处理，对Meng算法得到的边界约束图进行引导滤波，用得到的粗透射率与He算法的粗透射率进行比较再融合。最后，对融合后的粗透射率进行上下文正则化，得到精细化透射率，再通过大气散射模型得到去雾后的图像。

2.2 非线性增亮

煤矿是点光源照射环境，故先采用伽马校正对图像进行亮度调整。

式中：Igamma(x)为经过伽马校正后的有雾图像；γ为伽马因子，控制整个变换的缩放程度，γ=0.7。

伽马校正结果如图2所示。可看出，调整后的图像亮度更均匀。

图2 伽马校正结果Fig. 2 Results of Gamma correction

2.3 改进的大气光值估计方法

He算法采用的大气光值估计方法是直接选取暗通道中亮度值前0.1%的平均值，但是井下存在大片黑暗区域，造成暗通道中的亮度值都较小，选取的大气光值也较小。文献[11]提出的估计方法是选取暗通道图像开运算后的最大值。以上方法都是对暗通道图像进行处理（暗通道是对颜色通道进行最小值滤波后得到的），这使得暗通道图像的值均小于原图像颜色通道的值。本文直接对输入图像的颜色通道进行开运算处理，选取红绿蓝通道中最亮的区域值作为大气光值，这样能够降低去雾图像点光源区域的亮度，可以很好地抑制点光源照射。大气光值估计方法对比如图3所示。

图3 大气光值估计方法对比Fig. 3 Comparison of atmospheric light estimation algorithms

从图3可看出，He算法的估计方法出现了过曝光问题，极大地影响了对信息的识别。文献[11]及本文提出的估计方法差异并不明显。经过计算，He算法的估计方法得出的大气光值为[121,123,122]，文献[11]算法的估计方法得出的大气光值为[219,221,219]，本文提出的估计方法得出的大气光值为[234,233,234]。可看出本文提出的估计方法选取的大气光值更大，在煤矿环境中能够有效地抑制点光源照射。

2.4 引导滤波

针对Meng算法得到的边界约束图存在边界模糊的问题，本文引入引导滤波[13]，以保持边界清晰。

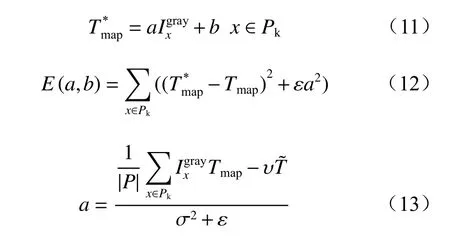
当x位于不同的窗口时，会存在不同的a，b值，所以要对以x为中心的窗口内a和b的值取平均，得到平均后的引导滤波。

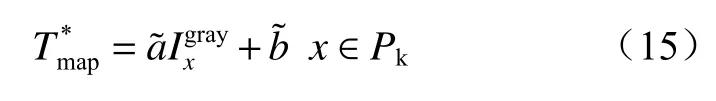
引导滤波结果如图4所示。可看出对边界约束图进行引导滤波后，边界约束图变得更加平滑，边界信息更加明显。

图4 引导滤波结果Fig. 4 Results of guiding filtering

2.5 粗透射率融合

如果将传统的Meng算法直接应用在煤矿井下，图像会出现透射率评估不正确的问题。因此，将He算法与Meng算法先进行比较然后再融合。这是因为Meng算法计算粗透射率时更加精细，但容易出现区域透射率评估不正确的问题；He算法通过暗通道来计算透射率，在井下黑暗的环境中，He算法对透射率的估计更加准确，但是其评估的透射率是成块的，透射率细节不够。如果直接对He算法与Meng算法的粗透射率进行融合，易导致透射率边界模糊，因此对He算法与Meng算法的粗透射率差值进行比较，当He算法和Meng算法的粗透射率差值小于阈值时，对He算法和Meng算法的粗透射率值取平均。当He算法和Meng算法的粗透射率差值大于阈值时，则取He算法和Meng算法中最小的粗透射率值。然后再对He算法和Meng算法的粗透射率进行融合，融合后的粗透射率为

式中：t1(x)，t2(x)分别为Meng算法与He算法的粗透射率值；Q为判定阈值，0＜Q＜1。

经过多次实验，发现当Q=0.1时，融合效果最好，实验结果如图5所示。可看出融合后的透射率克服了Meng算法相邻物体透射率不同的缺点。

图5 融合结果Fig. 5 Result of fusion

3 仿真结果与分析

3.1 主观评价

为了验证本文算法的有效性，对煤矿井下大量的有雾图像进行测试（由于篇幅限制，仅选择6张井下图像进行测试）。仿真结果如图6所示。可看出He算法虽然达到了一定的去雾效果，但在有点光源的图像中存在图像过曝光的问题。文献[9]的算法虽能够减小点光源照射的问题，但对尘雾较浓的图像去雾效果较差，且在去雾图像中的灯光处存在较多的蓝色圆环，说明此算法处理图像较亮区域时出现了颜色失真。Meng算法与文献[11]的算法对图像的细节处理得很好，但存在色彩对比度过饱和、颜色失真及整体颜色偏暗等问题。本文算法在有点光源的图像中没有出现过曝光的问题，还很好地保留了图像的细节信息，在灯光处出现的失真更少，对浓雾图像的处理效果优于其他算法，且本文算法去雾后的图像整体较亮、去雾效果更好。

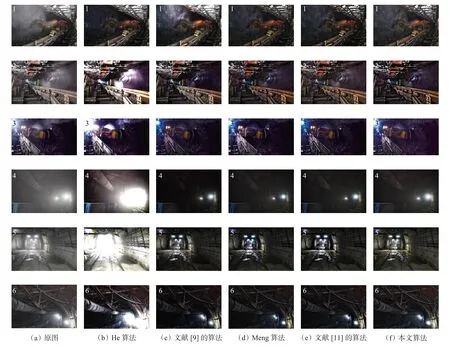
图6 去雾效果对比Fig. 6 Comparison of defogging effect

3.2 客观评价

为了验证本文算法的优异性，采用峰值信噪比（Peak Signal-to-Noise Ratio，PSNR）、结构相似性指标（Structural Similarity Index，SSIM）、特征相似性指标（Feature Similarity Index，FSIM）3种指标对各类算法的去雾效果进行客观评价，结果见表1。其中PSNR表征去雾图像的失真性，数值越大，代表图像失真越小；SSIM从图像亮度、对比度和结构对比度3个方面表征去雾效果，值越大，表示去雾效果越好；FSIM侧重图像的边缘保持，值越大，表示图像边缘保持更好。

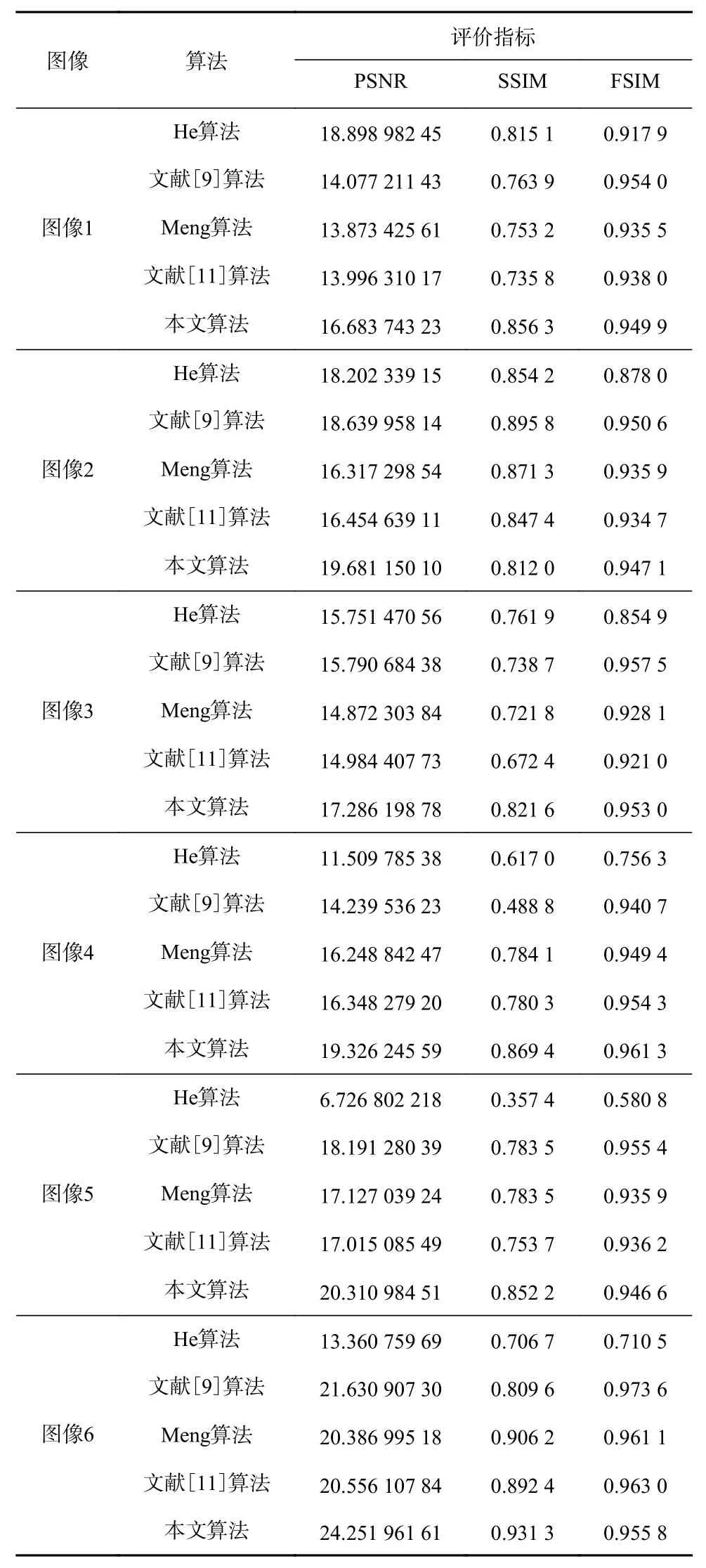
表1 不同算法去雾图像指标比较Table 1 Indicators comparison of defogging images processed by different algorithms

从表1可看出：在PSNR，SSIM ，FSIM参数上，本文算法相较于He算法分别平均提升了61.52%，36.51%，24.57%，相较于文献[9]的算法分别平均提升了15.51%，19.27%，-0.30%，相较于Meng算法分别平均提升了18.93%，7.19%，1.21%，相较于文献[11]的算法分别平均提升了18.29%，10.54%，1.19%。PSNR的提升说明本文算法得到的去雾后图像失真更小、细节信息更多。SSIM的提升说明了去雾后的图像更加明亮、对比度更加鲜明、图像结构保持得更好。FSIM的提升说明了本文算法在保留精细化的同时，还能很好地保留图像的边缘特征，具有一定的优异性。

4 结论

（1） 基于暗通道的大气光值估计方法应用到煤矿井下时，选取的大气光值较小，易造成图像过曝光、无法抑制点光源照射等问题。因此，提出直接对图像的红绿蓝三色通道做开运算处理，取开运算后通道图像的最大值作为大气光值，有效降低了点光源附近区域的亮度。

（2） 结合He算法在井下环境中评估透射率的准确性与Meng算法对细节信息处理的优异性，将两者的粗透射率差值进行比较，然后再融合得到粗透射率，利用上下文正则化对融合后的粗透射率细化，并通过大气散射模型得到去雾后的图像。

（3） 仿真结果表明，本文算法没有出现过曝光等问题，且对浓雾图像的处理效果更好，去雾后的图像也更加明亮，颜色更加接近原图。

（4） 本文去雾算法在PSNR，SSIM，FSIM上相较于He算法平均提升了61.52%，36.51%，24.57%，相较于文献[9]的算法平均提升了15.51%，19.27%，-0.30%，相较于Meng算法平均提升了18.93%，7.19%，1.21%，相较于文献[11]的算法平均提升了18.29%，10.54%，1.19%。说明本文去雾算法对煤矿井下图像的去雾效果更好、图像更加明亮、细节信息保留的更多，具有一定的优异性。