巧避材料暗示 促进深度学习——《三角形的面积》教学实践与思考

文 许燕萍 俞 军（特级教师）

【课前思考】

随着课程改革的不断深入，教师的教学理念也在不断更新。《三角形的面积》一课教学，广大教师已将重点从三角形面积公式的掌握和熟练运用转变为三角形面积公式的理解上，也看到很多案例中安排了大量的实践操作活动去探究面积公式的由来。

但如何在这些探究活动中充分暴露学生的原生态思维，拓宽他们的思维广度，最大限度地挖掘解决问题的多种策略，从而让学生深刻体验到知识产生的过程，让学生的数学学习真正发生，显然还有待深入研究。因此，笔者将从探究材料入手，不再提供给学生可操作的两个完全一样的三角形（分三类），而是让学生先想一想，然后再在《学习单》上画一画思考过程，并借助表达想法、动手操作、课件演示来更直观、更多元地展示图形的转化过程，从而拓展学生的思维空间，发展学生的空间想象力。

【教学目标】

1．经历三角形面积计算公式的推导过程，理解三角形面积计算公式的由来，并正确运用三角形面积计算公式进行计算。

2．进一步发展学生的空间想象力，体会转化的数学思想。

3．在自主探究中获得积极的情感体验，进一步培养学习数学的兴趣。

【教学过程】

一、激活已有经验，适时导入课题

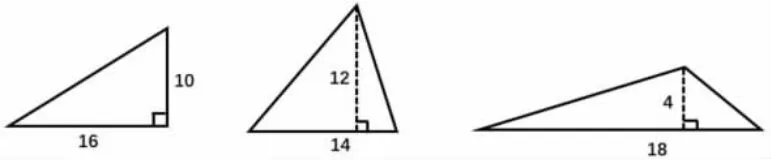
上课伊始，教师借助多媒体直接出示上面三类三角形（先不给数据），问学生：你看到了什么？（生：直角三角形、锐角三角形、钝角三角形）

（然后课件出示数据）你又看到了什么？（生：三角形的底和高分别是多少）好的，今天我们就一起来研究三角形的面积。（板书课题）

【思考：上课伊始，教师直接出示三种不同类型的三角形，在没有数据的干扰下，促使学生回忆起三角形的分类，有效激活已有经验，为本节课将要从这三类三角形展开研究做铺垫。另外，开门见山引入课题，有效激发了学生的探究欲望，使他们迅速将思维转移到本节课的研究内容上。】

二、直面挑战性任务，暴露学生思维

师：同学们，如果让你任选一类三角形来研究，你会选哪个？（生:直角三角形）现在我们要研究直角三角形的面积，你会怎么想？先把你的想法在这个直角三角形上画一画，然后再算一算，请完成《学习单》的第一题。（学生独立探究，教师关注学生探究的情况，及时了解学生的探究过程及计算背后的思考过程）

【思考：以上教学环节，看似无意，实则别有用心。在以往的教学过程中，教师通常会为学生准备好类似这样的学具：提供两个完全一样的三角形（分三类）。从前期的磨课中发现，这样的安排无意中局限了学生的思维，使其在想到拼组的方法后很难再去思考别的方法。因此，我们决定不再为学生提供两个完全一样的三角形，而是让学生先想一想，再把思考过程在《学习单》上的直角三角形中画出来，由于学生已有的活动经验和思考的角度不同，解决问题的策略也不尽相同，故此环节为学生有效创设了探究的时空，能充分暴露学生的原生态思维。】

（教师巡视并找到学生的以下三种转化方法，并逐个投影反馈）

师：同学们，请看大屏幕，有同学是这么做的（指着图1），谁能看明白？

师：（追问）随便两个直角三角形都能拼吗？（两个完全一样的直角三角形才可以拼）

师：老师这里就有两个完全一样的直角三角形，按照你的意思把它拼成长方形（紧接着教师用实物演示，并贴到黑板上）。刚才我们这样拼是拼成了（生：长方形），如果这样拼就拼成了（生：平行四边形）。

师：（追问）但这两种拼法都可以用哪个算式来计算？（16×10÷2）

师：下面我们来看第二种想法（指着图2），先请主人来说说他是怎么想的。（生：我是沿高的一半剪开，然后把它拼成一个长方形）

师：（追问）高的一半怎么找呢？谁有好办法！（生：对折）好，那老师把它沿着高对折，（教师沿着高剪开）谁来帮老师拼一拼？（指名学生拼贴到黑板上）

师：现在我们把这个直角三角形转化成了长方形，这个长方形的长是（16），宽是（10÷2），面积是16×（10÷2），这样算出来的也就是（生：三角形的面积）。

师：同学们，这里还有第三种方法（指着图3），猜猜他又是怎么想的？（他是沿着底的一半剪开，再把剪下来的左边部分拼到上面，也拼成了一个长方形）

师：（追问）那底的一半怎么找啊？（生：也用对折）好，老师就照着你的意思对折并剪下来（教师演示），这次谁来帮我拼？（指名学生贴到黑板上）

师：（追问）这个长方形的面积怎么计算呢？（生：16÷2×10）这样也就算出了（生：三角形的面积）。

小结：我们在研究直角三角形面积的时候，可以用两个完全一样的直角三角形拼成一个长方形或者平行四边形，也可以将一个直角三角形割补成一个长方形，但是不管哪种方法，都是转化成了我们已经学过的图形。

【思考：以上教学过程，教师利用印在《学习单》上的直角三角形这一探究材料，促使学生多角度地思考问题，激活了学生的多元思维，体会到了解决问题策略的多样化，有效提高了学生解决问题的能力。同时，还适时渗透了转化的数学思想。另外，在师生、生生间的交流、互动、碰撞中，学生的思维从模糊到清晰，从残缺到完整，甚至从错误到正确，从而不断完善了学生的思维。】

三、紧扣数学本质，完善学生思维

师：同学们，我们继续学习，请看大屏幕，现在还剩下哪两类图形？（生：锐角三角形和钝角三角形）同桌商量一下，一人选一个，先画一画，再算一算。请拿出《学习单》来试一试，做完后可以同桌交流一下各自的想法。

教师在巡视中有意识地选择锐角三角形的三种典型计算方法，并请学生板书到黑板上，具体如下：

方法①：14×12÷2 方法②：14×（12÷2）

方法③：14÷2×12

师：好，同学们，请停下来！我们先来交流锐角三角形。你能看懂哪一种？

（学生交流到方法①时投影《学习单》的相应思考过程，出示图4）

师：（交流到方法②时）猜猜他是怎么剪的？还有不同的剪拼方法吗？（教师根据学生汇报交流，适时呈现如图5的两种方法）

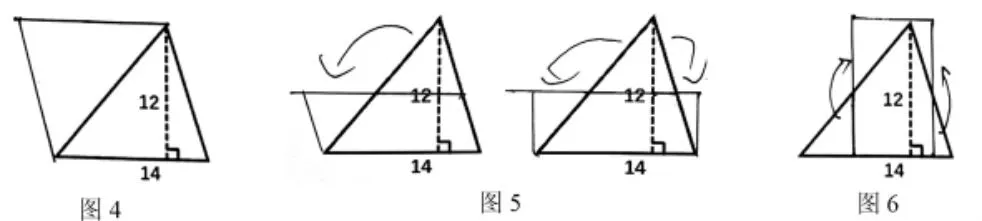
师：（继续引导）不难发现这两种方法都是沿着高的一半剪开，拼好的图形和原来的三角形面积是（生：相等的），所以这个三角形的面积该怎么算？（生：12÷2×14）。

师：（交流到方法③时）他又是怎么想的呢？（生：沿底的一半剪开，但是不能对折，要两边分别对折剪开）（教师适时出示图6）所以这个长方形的长是（生：14÷2），宽是（生：12），算式是（生：14÷2×12）。

师：还有同学选择了钝角三角形来研究，我们一起来交流（快速简单交流）。

教师逐一呈现学生中典型的三种转化方法（如图7）：

师：同学们，你们真了不起！现在我们一起以动态的方式来回顾刚才的这几种转化过程。（教师课件动态演示转化过程，如图8）

师：同学们，你们很厉害！想到了那么多的转化方法，那么现在你们说一说三角形的面积可以怎么计算呢？（生：底×高÷2）这个呢？［生：底×（高÷2）］这个呢？（生：底÷2×高）其实，这三个公式的本质是一样的，一般情况下，三角形的面积公式就写成：底×高÷2；其字母公式可表示为：S＝ah÷2。

【思考：在探究完直角三角形之后，引导学生自主探究其余两类三角形的面积，学生在已有的直角三角形的活动经验上，能够自主利用方法再次迁移，由特殊到一般，从而让推理过程更严密。另外，通过大量的对三角形面积转化过程的体验与感悟，使学生对三角形面积公式的理解更为清晰和深刻，真正构建起了三角形面积计算的模型，从而进一步有效促进了学生的深度学习。】

四、延长体验过程，强化数学思维

师：（课件呈现基本练习）同学们，你们学得都很棒！现在老师要来考考你，请看屏幕（课件出现原始三角形，如图9）。

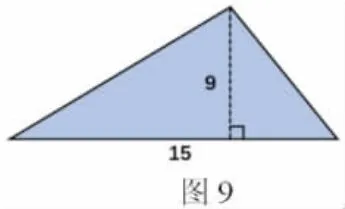
师：如果让你计算这个三角形的面积，你会想到哪些转化方法？静静地想一想。（让学生只在脑海中想，不作交流）

师：（课件出示图10-①）这种转化方法你想到了吗？（课件出示图10-②）这种转化方法你又想到了吗？（课件出示图10-③）现在呢？（课件出示图10-④）最后一个呢？

师：（再出示图10中右边三个算式）现在请你将转化的方法和匹配的算式连一连。

师：同学们，请看大屏幕，和你连的一样的请举手。很棒！为你们点赞！

【思考：通过先想象，后找到转化的方法，并和匹配的算式连一连，旨在引导学生进一步体验、强化解决“三角形的面积是多少”这个问题的思维方式，而不是简单、机械地套用公式，学生感悟到的是一种数学本质，而非一个冷冰冰的公式。】

五、适时拓展延伸，提升学生思维

（课件呈现拓展练习）请你在下图中画一个三角形，使得它的面积与平行四边形的面积相等。（每相邻两点之间的距离为1）

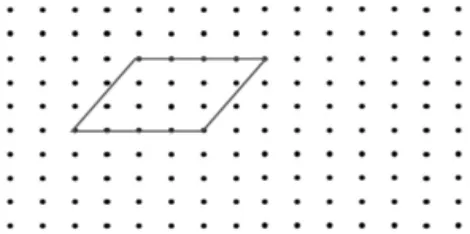
师：看来，这些数学问题都难不倒大家！下面我们继续研究。请看大屏幕，自由地读一读要求。

师：同学们，题目读完了，会吗？请在《学习单》上试一试。

反馈预设：

1.展示底是4，高是6的作品（图略）。我们先来看这位同学的作品，先请他说说是怎么想的？

生：当三角形的面积和平行四边形的面积相等，并且底也相等时，那么三角形的高必须是平行四边形的高的2倍，这样才能保证它们的面积相等。

2.展示高是3，底是8的作品（图略）。我们再来看第二位同学的作品，谁能猜猜他是怎么想的？

生：当三角形的面积和平行四边形的面积相等，并且高也相等时，三角形的底必须是平行四边形的底的2倍，这样才能确保它们的面积相等。

3.展示底×高＝24的作品（图略）。我们再来看这位同学的作品，请作者说说他又是怎么想的？

生：要保证三角形的面积与平行四边形的面积相等，只要做到“底×高＝24”，然后再÷2就可以了。

【思考：表面上这是一个实践操作题，但是考查的却是学生的空间想象能力，万变不离其宗的思维方式，以及逆向思考的能力。即无论怎样想象及如何画图，只要三角形的面积算出来等于12就行；同时，还可以逆向思考，三角形的底乘高除以2等于12，那么底乘高只要等于24即可；还有当三角形的底和平行四边形的底相等时，高必须是两倍关系才能保证它们的面积相等，从而有效提升了学生的数学思维和关键能力。】

六、渗透举一反三，发展提问能力

师：好了，同学们，到现在为止我们已经学会了如何求长方形、正方形、平行四边形和三角形的面积，此时你又有什么新的问题要问老师或同学吗？

生1：梯形的面积怎么求？

生2：圆的面积怎么求……

【思考：通过学生的提问，构建起长方形、正方形、平行四边形、三角形、梯形和圆的整体框架，为后续学习梯形的面积、圆的面积做好铺垫，同时也培养了学生的知识迁移能力。】

【课后思考】

1.精设探究材料，开放学生思维。

材料引起学习、材料引起活动，学习材料是我们解决问题和形成数学思维的基本保证。本课最大的特点是探究性学习材料的精心设计，没有像大多数教师一样给学生提供两个完全相同的三角形（分三类提供），而是呈现给学生三个不同类型的三角形，引导学生通过想一想、画一画、算一算的数学活动，完成三角形面积公式的推导。在此活动中，学生的思维不受学习材料的影响，可以想到用两个完全一样的三角形进行拼组，也可以想到把一个三角形进行剪拼，避免了不敢剪、剪坏了没有材料可用的尴尬场面。另外，“先想再画”对学生的空间想象能力提出了更高的要求，但它能充分暴露学生的原始思维，有效提升学生的想象能力和思维能力。

2.遵循学习轨迹，实现顺学而导。

从学生思考的角度出发,更容易发现问题,而问题本身往往就是教学重难点。本堂课，教师始终遵循学生学习的思维轨迹，通过画一画的独立思考，充分暴露学生的原始思维，在与他人交流的过程中，不断积累思维的经验，逐步形成自己的合理的思维方法，真正实现了顺学而导的教学理念。只有当学生通过自己的思考，建立起自己的数学理解力时，他们才能真正学好数学。

3.设计多元体验，促进深度建模。

本节课中，教师设计了两个多向思维的环节，如探究直角三角形的面积时，由思维图式得到计算的算式，而在锐角三角形和钝角三角形时，却由计算的算式回忆或猜想思考的过程。又如练习设计，第一个基本练习是根据推导方法选择匹配的算式，在解决问题的过程中学生不再是简单地套用公式，而是重现转化过程，进一步理解三角形面积计算公式的数学内涵。第二个拓展练习是根据三角形的面积公式反推底和高，通过推导、说理等过程，找到平行四边形和三角形面积之间的内在联系。这样的多元体验，贵在引导学生从多层次多角度去思考问题，不仅能强化教学重点，突破教学难点，而且还可以激发学生的学习兴趣，充分发挥出每一位学生的学习潜能，有效培养了每一位学生的创造力。

总之，科学的、客观的、具有一定开放性的学习材料，能够让学生的数学思维充分拓展，解题策略丰富多元，从而让学生的数学学习真正发生。