基于微惯性传感器的胸外按压深度检测

张正 谭朋柳 徐光勇

（南昌航空大学软件学院 江西省南昌市 330063）

自上世纪以来，随生生活环境的变化人类心脑血管疾病发病率成高趋势发展，心脏性疾病成为了威胁人类健康的重大杀手之一，发病率较高且大多发生在院外。故心肺复苏治疗(cardiopulmonary resuscitation,CPR)的有效实施是治疗心脏骤停的重要方法，使该类患者生还的唯一机会。可是心肺复苏术操作复杂，在紧急的院外环境下医务人员很难满足《国际心肺复苏指南2010》中规定的胸腔下陷5cm以上的要求并且由于医务人员因操作不当导致倾斜按压下大大降低按压有效性，很难测得垂直按压深度。所以，精确地检测按压深度对提高病患的生存率所具有的至关重要的涵义。

在胸外按压过程中，由于急救人员的按压姿势错误而常常会出现按压偏斜现象，由此导致加速度仪等传感器敏感轴的输出并非垂直重力加速度。在实际情况中，给专业急救人员提供是否按压倾斜并没有太大的实际意义，本文所研究的就是在特殊按压情况下提高按压深度精度。将MEMS传感器采集到的数据需要零偏校正，去噪以及卡尔曼滤波和融合处理。针对按压过程中的倾斜按压问题，而本文使用微型加速度计和陀螺仪相结合姿态角求解垂直方向上的真实位移。这大大减小了因倾斜按压导致的深度检测误差，更精准的给急救人员施救反馈，本文胸外按压深度解算流程图如图1所示。

图1：胸外按压深度解算流程图

2 按压装置系统的坐标系与姿态描述

作为在定向、导航、姿态分析系统中的新生力量，微惯性传感器使导航精确度获得了提升和发展。在作业和分析试验时，首先，要以借助各种类型的坐标系统来定位确定微惯性的导航体系，并判断目标物体的运动姿态或轨迹。在通常具体情况下，人们使用的较多的坐标系为惯性坐标系。

除了以上最常用的惯性坐标系之外，还有一种就是载体坐标系，该坐标系也是本课题实验中胸外按压姿态检测的参考坐标系，任一类型的载体坐标系伴随载体随之而动。载体坐标系中存在俯仰角φ、翻滚角θ、偏航角ψ，三种不同类型的角分别绕X轴、Y轴、Z轴进行旋转，均为研究要利用的姿态角研究数据源。

3 基于微惯性传感器的按压倾斜角检测

在急救人员对接患者进行胸外按压时，双手应与胸骨呈垂直状态进行按压。可是紧急情况下不规范的倾斜按压会出现不规范的二维倾斜与三维按压倾斜，示意图如图2所示。检测胸外按压的垂直性是本文研究的重点。本文在基于加速度计和陀螺仪的MPU6050传感器下，先用加速度计自身具有的倾斜角度计算功能获得初始的姿态角，对计算获得的姿态角和陀螺仪的转动速率引入了卡尔曼融合获得的终极姿态角，也便是通过滤波器处理后的姿态角。

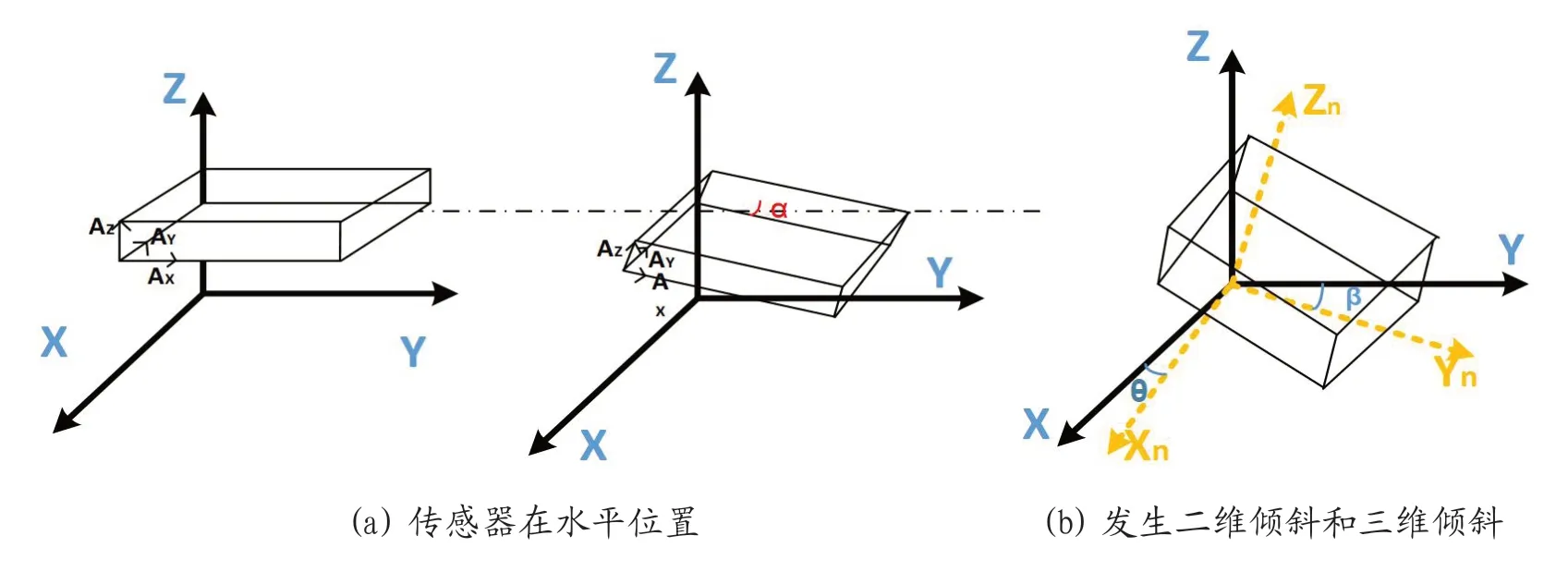
图2：倾斜按压模块空间示意模型

3.1 加速度计解算初级姿态角

加速度传感器测量的值是相对于载体坐标系(也称为传感器坐标系)。当载体传感器运动时，我们只关注绕X轴与Y轴相对水平坐标系的角度变化，因为绕Z轴发生旋转偏移时，Z轴与垂直方向的角度是不变的。

对按压加速度波形进行分析，在按压的终点（即按压最深处）加速度传感器几乎可以忽略外力施压的加速度值，经过分析，在短距离的按压过程中，开始和按压最深处倾斜角度可以认为是一致的，我们对此时的敏感轴加速度值进行分析。

假设当加速度计沿着Y旋转时，重力与X、Y轴之间的夹角和X、Y轴的加速度关系可以表示为：

A和A分别为敏感轴Z和X的输出，g为重力加速度。所以倾角可以由反正切得到：

当加速度计发生三维倾斜时，此时重力加速度g可表示为：

按照O-XY平面按压前后倾斜的角度α等于a和g间的角度，故有：

3.2 卡尔曼融合解算终极姿态角

本研究将急救人员在胸外按压过程中，按压最低点进行姿态角的求解，用于最后求解重力方向的按压位移。将由加速度计得到的初级姿态角和陀螺仪输出角速度值相结合，使用卡尔曼融合，求出终极姿态角。

本研究卡尔曼滤波算法模型如下：

状态空间方程：

观测方程为：

其中状态量X=[Angle Q_bias]，Angle是我们要求的卡尔曼融合后的倾斜角，Q_bias是陀螺仪的漂移值，Y代表了由上述加速度仪获得的姿态角的观察值，U即控制量，为陀螺仪所提供的角速率值。

R为观测噪声向量，它表示由按压测量时加速度传感器得到的姿态角观测值的噪声方差，用来描述系统在过程中对于加速度传感器的信任程度，如果R的值很小，观测值的质量很好，最终要求的姿态角对观测值的信任程度大。Q为整个需要估计的系统噪声的协方差矩阵，这里的噪声有两种：系统要预测的姿态角和角速度值。

角度的预测值Angle：

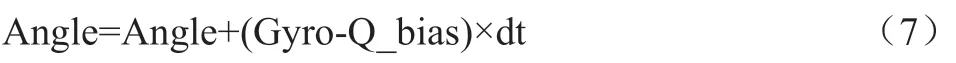
此算法公式要引起关注的是两边的角度类型必须相同。

现在根据滤波过程和数学模型得到状态预测：

先验估计

假设现在的状态为k，根据上一时刻的状态k-1预测出现在的状态：

预测协方差矩阵

系统的结果已经更新，而现在状态的协方差P还没有更新：

计算卡尔曼增益

通过卡尔曼增益来修正误差

更新协方差矩阵

现在为止，状态的最优估计值都已获得，不过想要将卡尔曼滤波继续迭代下去直到完成，就必须修改协方差矩阵。

4 胸外按压深度检测

在院外或在急救车上，心跳或呼吸骤停的病人假设平卧在水平面上，若知道物体双手互相按压的加速度，即可使用加速度二次微分计算中的梯形积分方式求出物体的位移，即可知道按压过程中的位移量。

4.1 二次积分法求解位移

在胸外按压进行之前，将按压数据收集设备放置在病人胸前，本文抽取1200个重加速度计z轴线方向的数值进行平均值计算以减少噪声影响，从而获取最准确的加速度仪零点偏移量。在人工按压过程中，利用相对较为精确地梯形积分算法按照以下公式对采样的数据进行积分：

其中Δt为采样间隔时间，运用梯形公式积分，由加速度信号a(i)(i=0,1,2,…,n)可得速度信号：

位移信号如下：

4.2 积分位移与倾斜角结合

在完成了上述的工作后，我们得到了加速度计Z轴输出值经过积分算法后的位移，因为在急救人员的实际按压操作不规范导致的倾斜按压，接下来只需将位移与倾斜角结合，计算出重力方向上的真实按压位移，算法公式如下：

上式中，S代表要计算得出的重力方向上的按压位移，d代表积分算法得出的Z轴方向按压的位移，上式中的翻滚角和俯仰角为按压到胸腔最底端时计算所得。

5 实验方法与分析

5.1 实验方法

为了对以上方案的验证，本次实验采用心肺复苏模拟按压人、MPU6050传感器模块、USB数据通信模块、树莓派核心处理器模块和PC机搭建实验平台进行仿真实验。

树莓派4B是一种三十二位具有4GB的闪存空间的微型电脑，工作频率可调性较高，接口多种功能丰富，系统集成度较高。信号检测部分使用了三轴的紧凑型MEMS陀螺仪和加速度计集成模块MPU6050，MPU6050是一种由三轴加速度和三轴陀螺仪所构成的六轴运动跟踪感应器。加速度仪选用±8g的最大量程，而陀螺仪则采用±2000°/s，在将波特率设定为9600Hz的工作状态下，利用树莓派芯片的串口传送有关MPU6050的信息给上位机，并收集七百组信息后再通过MATLAB程序对数据的信息进行生成波形分析处理。将MPU6050水平安放时，在静止环境条件中，姿态角的理想数值是0°。

5.2 实验仿真结果分析

图3为我们在实验平台使用MPU6050采集的加速度进行的加速度曲线特征点识别。如实验采取数据时，在实验胸外按压的开始点，最深处特性点，按压后完全回弹的特性点，本研究人员从上述特性点处对运动学参数作出了解析。实测中，我们所采集的胸外按摩加速度波形如图显示，有典型的在按摩过程中的起始点(starting point)，此时加速度阈值开始向偏离基线位置的快速降低。在解算中本文设定了相应程度的加速度阈值，便于在后期加速度值低于此阈值时开始积分。按压至最高点(maximum compression point)，是指由于按压至最深处，加速度急剧增大而形成波形的拐点所在。按压的终止点(ending point)意思是在按压完成后，加速度开始慢慢回复到原来停止状态的基线处。

图3：加速度曲线特征点识别

本次仿真中，特征点识别和积分后的位移检测结果如图4，图4为11个60mm的预设深度检测结果（本研究中所用的心肺复苏人胸腔最深为60mm），最大的按压误差为3.88mm，最小按压误差为2.95mm。

图4：胸外按压深度检测结果

利用本次研究的胸外按压检测实验平台，作者使用高精准位移标定仪，在30mm、40mm、50mm和60mm四个位置进行标记，作为标准位移参考。分别在四个参考位移位置进行三十次按压，分别使用传统的单一二重积分算法和本研究融入倾斜检测的算法，取平均数值对比实验反馈系统深度，计算绝对位移和相对位移误差，实验结果得表1、2。

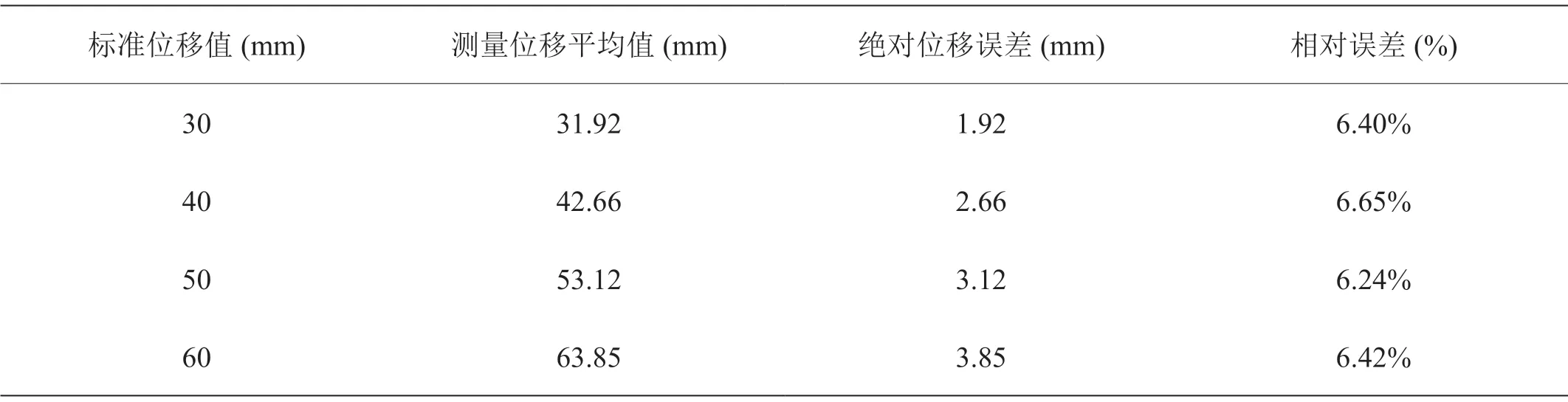
表1：二重积分算法下位移数据与标准位移比较

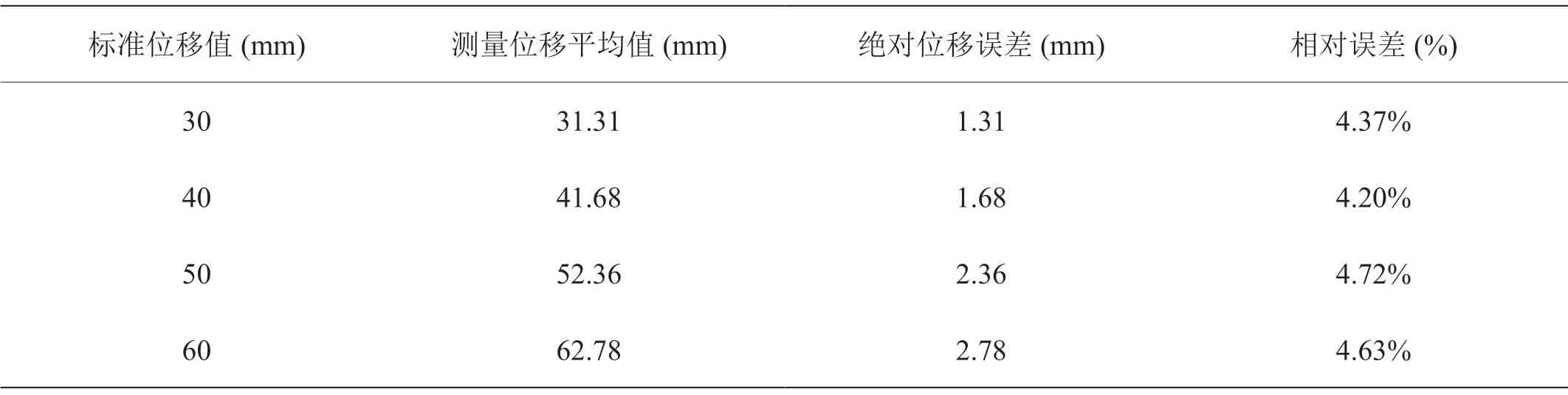
表2：加入按压姿态角下位移数据与标准位移比较

通过表1、2可以看出，二重积分算法下位移数据与标准位移比较位移比较，有所差异，相对误差在6.4%左右，但是在加入倾斜角考虑后，通过卡尔曼滤波获得姿态角，再进行位移解算，相对误差在4.4%左右，比传统位移算法相对误差减小了许多，精度提高。

6 结论

针对胸外按压效率低下的实景情况，为了提高按压深度的准确度，本研究采用MEMS三轴加速度和陀螺仪传感器MPU6050作为胸外按压深度的检测元件并设计算法计算。经过胸外按压实验测试得知，陀螺仪存在较大的漂移，对按压倾斜角的测量产生影响，而单一加速度计在倾角测量中受周围环境影响存在高频振动。本文在采用零点校准算法，梯形积分算法，创新性的加入了卡尔曼滤波算法，既可以补偿陀螺仪的漂移偏离，也克服了对加速度计的影响，从而更好的减少了MEMS传感器积分累计偏离和微分偏移误差。通过以上所述算法处理结果，很好的减少了由于倾斜按压所引起的按压深浅检测偏差，较现行的深度检测方法一般偏差小，更可以适应于现代临床上胸外按压深度检测应用的需要。