基于权重自适应鲸鱼优化算法的多能系统储能电站最优配置

在“碳中和、碳达峰”目标的引领之下，能源革命面临新的机遇，风电、光伏等新能源形式虽然在一定程度上优化了产业结构，并可加快“双碳”目标的实现速度

。但新能源发电固有的随机性和波动性使得大规模并网后系统的调峰压力加重，对电力系统的稳定性将产生较大的冲击。此外，火电机组在深度调峰时，按现有的调峰补偿制度难以满足火电厂的调峰成本，其调峰成本主要在于燃煤成本的大幅提升。根据文献[2]的计算结果，对于300 MW火电机组，当调峰深度从55%增加到40%时，机组能耗单位容量平均成本增加314515元/kWh；当调峰深度从40%增加到20%时，机组能耗单位容量平均成本增加715300 元/kWh。对于600 MW 火电机组，当调峰深度从50%增加到40%时，机组能耗单位容量平均成本增加406500元/kWh；当调峰深度从40%增加到20%时，机组能耗单位容量平均成本增加554500元/kWh。可见在火电机组参与深度调峰辅助服务时，火电厂承受较大经济负担，对于能源发电厂更为有利。储能系统具有响应速度快、可调节性强等特点，对于解决新能源出力间歇性、电网稳定调节等问题提供了一种新的解决方案，是实现“双碳”目标和能源革命的关键支撑技术。但目前储能系统配置成本较高，故不能大批量建设，因此，如何合理规划有限储能电站的位置，更好地为电力系统服务成为一个重要的研究方向

。

针对包含光伏发电、风力发电和典型负荷的电力系统，储能系统一般与可再生能源发电系统配合使用，例如在风电场并网处加入储能系统可以有效平抑风电并网功率波动

。储能系统的容量及选址配置是设计规划中的重要问题。文献[7]提出了一种滑动平均和标准校正的组合方法，分离出风电的并网分量和波动分量，然后采用小波分解得到电池和超级电容器的配置容量。上述文献均是以平抑新能源出力的波动性为优化目标，并未考虑储能系统的剩余寿命及成本等因素。文献[8]综合考虑风光储联合发电系统的稳定性和经济性，提出一种双层决策模型的储能容量配置方法。文献[9]建立了以节点电压波动、负荷波动和储能系统总容量为目标的电网模型，采用优化的多目标粒子群算法求解储能的配置问题。文献[10]关于城市电动汽车建造充电站的选址和容量问题提出了一种混沌模拟退火粒子群优化算法，该算法引入混沌理论，综合充电桩运营商，车主和发电商多方利益后建立模型。文献[11]考虑可再生能源出力的不确定性，建立了分支定界法及遗传算法双层模型来解决储能电站选址定容问题。文献[12]选择分布式储能用于缓解传输网络的拥堵，描述了三阶段规划程序，可确定分布式储能单元的最佳位置和参数。考虑换流器功率等级和储能容量的投资成本，文献[13]提出了在多电压等级下确定分布式电池储能系统最优位置、能量容量和功率等级的方法，可实现技术经济最优的储能选址需求。文献[14]综合投资、使用和安装等成本，提出了基于遗传算法的双级优化方法，在电网系统的允许节点配置储能来减少光伏渗透引起的电压波动。而对于含有储能电站的电力系统的规划与控制策略，文献[15]设计了一种基于Benders 分解的变分算法和相应的收敛准则和增强策略，提出风电场、储能与输电网结合的规划方法，并采用机会约束优化算法。为了提高系统的可靠性及降低运行成本，文献[16]为了保障系统运行的经济性以及延长储能电池的使用寿命，满足良好的经济目标，建立了双层微电网储能规划模型，可有效避免储能电池过充或过放。如上述文献所述，国内外学者对于储能的优化配置问题多针对容量配置问题，而对于储能选址问题研究得较少。尤其在含有风电、光伏、火电及储能的电力系统中，储能的选址配置问题复杂度较高

，往往求解困难。

综上，在含有风电、光伏、火电及储能的电力系统中，为了减小调峰时火电机组的调节与启停成本，本文从储能辅助火电厂调峰的角度出发，综合考虑风-光-火-储多能系统的运行特性和约束条件，将火电厂的输出功率波动最小作为目标函数，基于权重自适应鲸鱼优化算法，对储能电站的容量及选址配置问题进行优化求解。然后以IEEE-33节点的电力系统为例，选取风-光-火-储多能系统的典型功率数据进行分析，求解得到储能电站的最优配置方案，并得到了储能电站充放电运行策略。

操作上，笔者建议的是采取逢低分批买入的策略，不建议大家总是试图想着一笔买在最低点，一笔卖在最高点。建议逢急跌、分批次、每次一点点的加仓建仓。同时，在介入前必须要做好相应的策略应对。每笔介入前，必须做到以下四点：

1 多能系统储能电站的最优配置模型

本文研究的多能系统由风电、光伏发电、火电、储能以及负荷等部分组成，结构如图1所示。

由于在空间科学材料实验中针对热电偶信号的精度要求在微伏级，因而对系统的抗干扰能力有着很高的要求。在硬件设计中，通过放大调理电路的设计，系统接地方式的选取以及相应的抗干扰设计，从而减少噪声对系统的影响，提高信号检测精度[1]。

1.1 储能电站选址配置的最优目标函数

由于风电、光伏在时间分布上具有随机性和波动性的特点，使得火电厂调峰压力增加。火电厂的大幅度调节与启停，一是成本很高，二是调节时间长，极端条件下不利于电力系统稳定。因此为提高综合效益和系统的稳定性，本文将多能系统中火电厂的输出功率波动最小作为储能配置的目标函数：

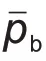
1.2 约束条件

式中，

(

)是

时刻的电价，

是储能运行单位成本，

是单位容量储能电站的造价。

（1）潮流及节点电压约束

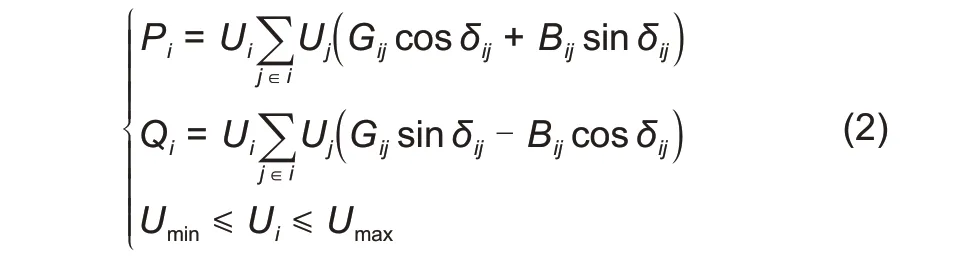
式中，

P

、

Q

分别为系统中节点

的有功、无功功率；

U

、

U

分别为节点

、

的电压幅值；

G

、

B

为节点

、

间的支路导纳；

δ

为节点

、

间的电压相角差；

和

分别为节点电压的最小和最大值。

（2）功率平衡约束

（3）传输容量约束

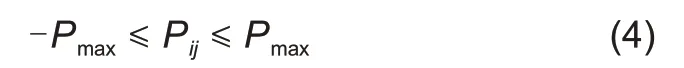
式中，

P

是

节点和

节点之间的线路潮流；

最大线路传输容量。

（4）风电、光伏出力约束

推进《黑龙江省节约用水条例》《黑龙江省地下水管理办法》立法，印发《黑龙江省“十三五”节水型社会建设规划》《县域节水型社会达标建设工作实施方案(2017—2020年)》，节水规划体系进一步完善。

式中，

(

)为从当前种群中选择个体的随机位置向量。

（5）储能电站的约束

观察对比组间护理效果(VAS评分、SDS评分、QOL评分)和恢复情况(住院费用、住院时间)差异评价结果[3]。

1.3 储能系统模型

储能电池的充放电特性可由以下参数描述：容量、功率、充/放电效率、自放电率和SOC。电池储能系统的SOC 代表电池剩余电量占额定电量的百分比，

时刻电池的SOC(

)计算式如下：

式中，

(

)为

时刻电池的剩余电量；

是储能电池容量。

目前临床尚未完全明确慢性支气管炎发病机制，普遍认为该疾病的产生与有害气体、有害颗粒入侵有关，支原体、病毒和细菌感染同样是该疾病产生的重要原因。慢性支气管炎病程长，临床症状主要表现为咳嗽、咳痰，同时伴随不同程度喘息，每年发病时间超过3个月，发病时间为2年或2年以上，发病早期异常症状不明显，可在患者急性发作期听到肺部干湿啰音，合并哮喘者可有广泛哮鸣音出现。

储能电站的充放电功率特性如下：

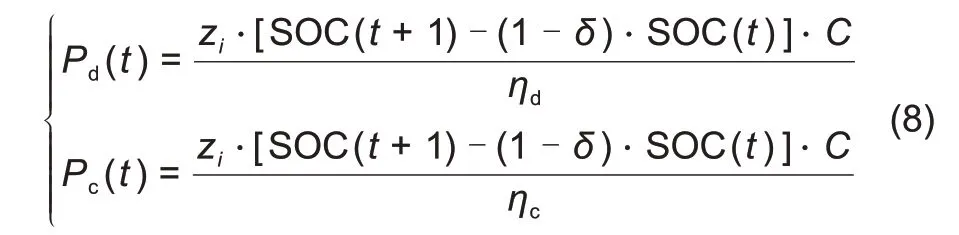
式中，

(

)和

(

)分别代表储能电站的放电和充电功率；

是自放电率；

和

分别是放电和充电效率；

z

是

节点的储能配置变量，含义如下：

储能系统的运行成本

，包括储能电站损耗成本以及储能电站投产需要的资金计算式如下：

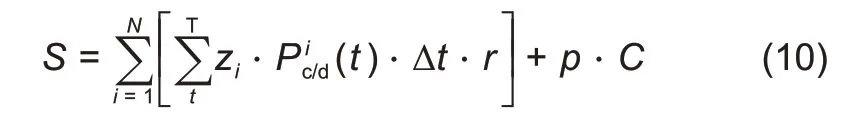
储能优化配置的约束条件主要有两类：一类约束是电力系统和储能电站的设备特性约束，例如各节点电压也要满足上下限约束，以及为了防止电池的过充和过放，荷电状态(SOC)和储能充放电功率必须满足上下限约束；另一类是系统在运行过程中需要满足的条件，例如应保证系统功率平衡等。这些约束条件表示如下：

2 储能电站最优配置求解方法

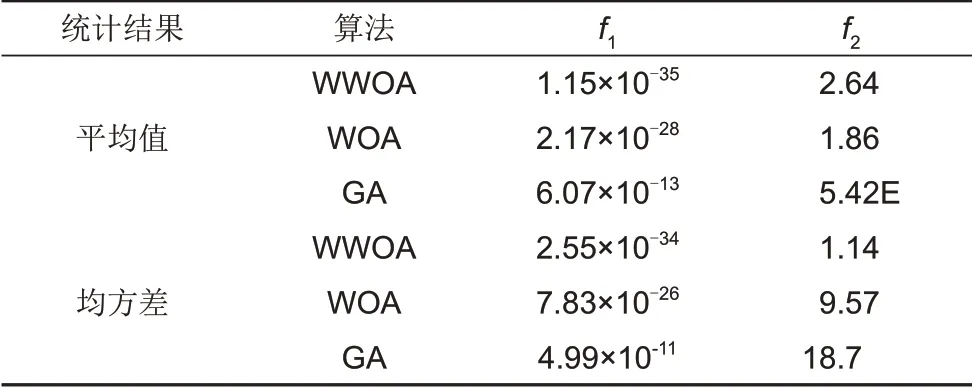
利用Matlab 2020a，将待检验的3种算法分别对标准测试函数独立重复寻优50 次，得到各算法寻优能力的平均值和均方差，如表2所示。可以看出WWOA相比于标准WOA算法和GA算法，在寻优

时精度远大于另外两种算法；在寻优

时，虽然寻优精度相差不大，甚至比标准WOA还要略低，但寻优的均方差比WOA 和GA 要小，说明算法的稳定性更好。

2.1 鲸鱼优化算法

鲸鱼优化算法(whale optimization algorithm，WOA)是2016年由澳大利亚格里菲斯大学的Mirjalili等模仿座头鲸狩猎行为而提出的一种新型启发式优化算法

。WOA主要由包围猎物(encircling prey)，气泡攻击(bubble-net attacting)以及寻找猎物(search for prey)三部分组成。

5个载体通过农杆菌介导瞬时转化洋葱内表皮细胞，GUS染色结果（图6）表明：除了GGPPS启动子全长活性略弱外，其余几个缺失片段活性均很强，能够高效驱动下游GUS基因的表达，且表达水平与CaMV 35S启动子基本一致，这表明该启动子的核心区域在上游518 bp以内。同时将GGPPS启动子全长与其他3个缺失启动子驱动GUS蛋白表达结果相比较，可以初步预测在上游1 131～1 052 bp可能存在着某些负的调控元件或诱导元件。相反，在上游1 052～518 bp，则存在着较多的增强子，在转录表达过程中发挥的促进作用也就越大。

座头鲸在狩猎时要包围猎物，该行为可用如下模型描述：

式中，

(

)是当前鲸鱼个体位置向量；

(

)是当前最优解位置；

为当前鲸鱼个体与最优位置之间的距离；

代表当前迭代次数；系数向量

和

由下式确定：

式中，

在迭代过程中由2 呈线性减小到0；

为0～1之间的随机向量。

专题教学可以是同一作者相似作品连类而成的学习，比如，学习苏轼的《前赤壁赋》时，和《后赤壁赋》进行比较阅读；学习莫泊桑的《项链》时，和其《珠宝》进行比较阅读。相对于《前赤壁赋》和《项链》的单篇学习，这样的比较阅读会让学生更好地把握单篇的特点，丰富对作者及作品的认识。

（2）气泡攻击

根据座头鲸的狩猎行为，狩猎时其是以螺旋运动游向猎物，数学模型如下：

（1）包围猎物

式中，

代表猎物和鲸鱼之间的距离；

是对数螺旋线的形状参数；

为0～1之间的随机数。鲸鱼以螺旋形状游向猎物的同时还要收缩包围圈，因此，在这种同步行为模型中，假设有

P

的概率选择收缩包围机制和1-

P

的概率选择螺旋模型来更新鲸鱼的位置，其数学描述如下：

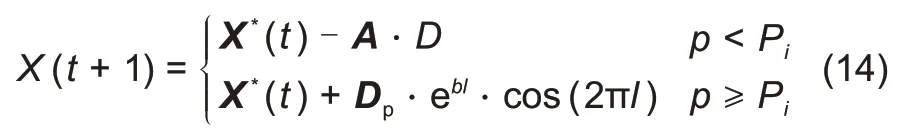
（3）搜索猎物

座头鲸除气泡攻击策略外，随机捕食也是一种重要手段。如果|

＞1，距离数据

将随机更新，说明座头鲸根据彼此的位置进行随机搜索，此时的捕猎模型为：

式中，

、

分别为风电、光伏的最小输出功率；

、

分别为风电、光伏的最大输出功率。

2.2 基于权重自适应的WOA改进

与其他智能算法相比，WOA 具有计算简单、收敛速度快、易于执行等优点，但也存在过早收敛以及易陷入局部最优等不足。尤其权重对算法影响明显：权重较大时，收敛速度较快，算法搜索范围较大；权重较小时，不易错过全局最优解，但收敛速度慢。因此有必要对权重进行自适应改进

。

在WOA 中引入非线性权重

和

，计算式如下：

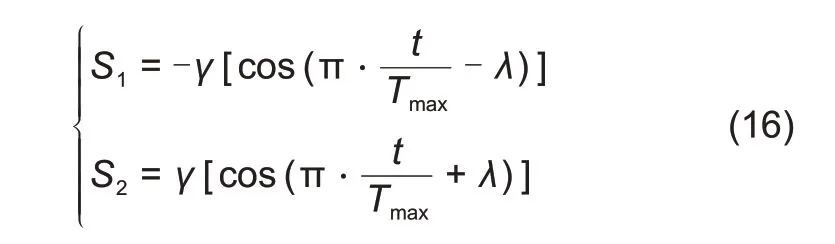
式中，

为

和

的取值范围；

为

和

的取值步长。

随迭代次数增加非线性递增，使种群能充分向最优位置移动；

随迭代次数增加非线性递减，在迭代后期有较小步长而加快收敛速度。

小型农田水利工程单体工程量较小、分布较为分散，增加了建设管理难度，特别是工程建设机械都要从农村农田中经过，工程进场道路不具备，农村河网密集，很多建设机械、建筑材料都要通过水路翻运，大大增加了施工成本。田间灌溉闸、防渗渠均建在农户庄稼中，与农民存在较大的矛盾协调工作。

将非线性权重

和

引入公式(14)～(15)，对包围猎物、气泡攻击及搜索猎物过程进行改进，得到：

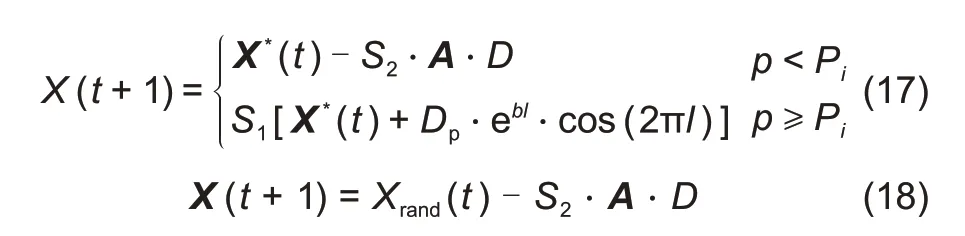
基于权重自适应改进的WOA(WWOA)流程如图2所示：

员工进入马来西亚后并拿到工作准证后，HSSE 部门要向马来西亚政府部门申请CIDB 培训，员工完成培训并考核合格，拿到经政府批准授予的CIDB 绿卡后，才真正具备进入施工现场的基本资格。培训内容主要为CIDB 重要性和历史发展背景、CIDB 卡个人信息备案情况、持有CIDB 卡人员必须具备的安全生产基本知识、必须遵守的安全规则、操作规程、雇主和雇员的安全职责，以及注册了CIDB 卡人员的保险享受条款等。

2.3 改进的WOA算法性能分析

本小节利用标准测试函数来对比WWOA、标准WOA 和遗传算法(genetic algorithm，GA)的性能。测试函数如表1 所示，最优值都为0。其中

是单峰函数，可检验算法的收敛速度和求解精度，

是多峰函数，可检验算法的全局探索能力。

储能电站的最优配置引入电力系统潮流方程，该方程为非线性规划问题，求解较困难，可用智能优化算法进行求解。

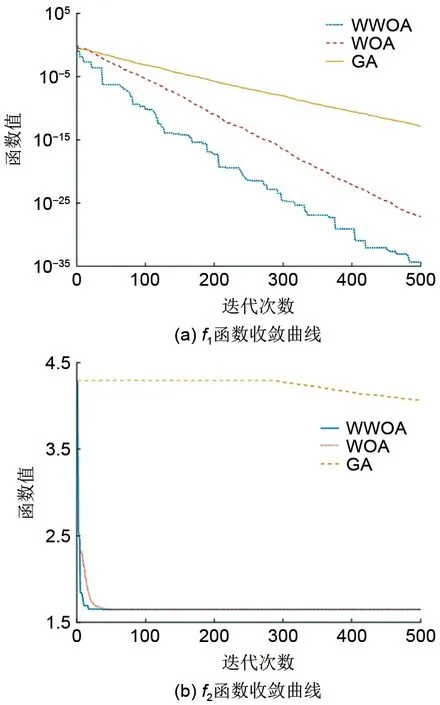
收敛曲线作为评价算法性能的重要指标。通过收敛曲线可分析算法在求解函数时的收敛速度、求解精度和全局搜索能力。图3为利用三种算法分别求解测试函数的收敛曲线图，可明显观察WWOA具有如下特点：收敛速度更快，收敛值低，这说明该算法求解精度较高；收敛曲线先出现拐点说明全局搜索能力更强。

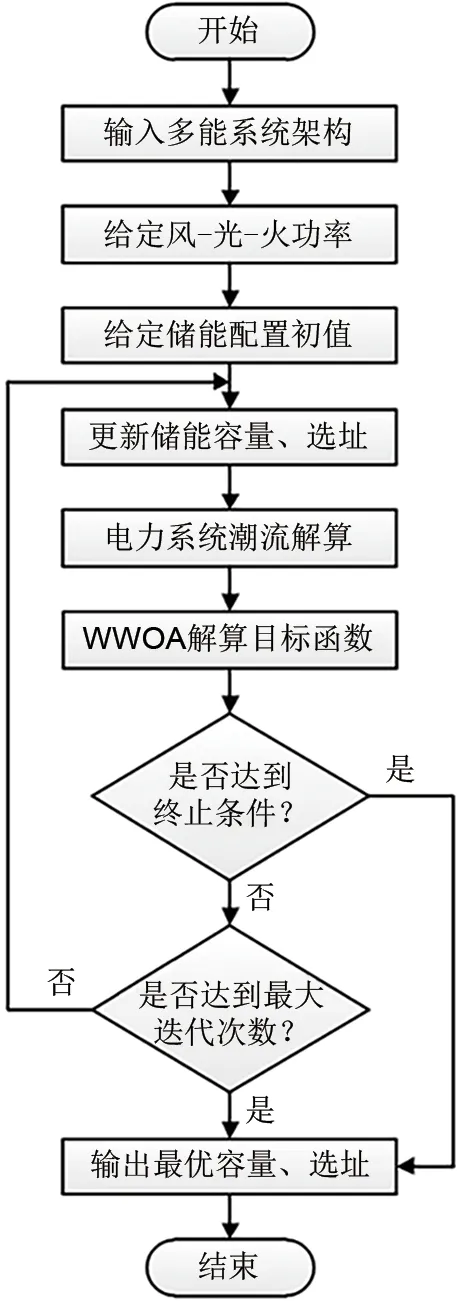
2.4 储能最优配置流程

图4 为风-光-火-储多能系统储能优化配置流程，配置算法采用WWOA 代求解，最终得到储能电站的最优容量和位置。

3 算例分析

本文采用IEEE-33节点电力系统来进行仿真分析，其结构如图5 所示。模拟的多能系统配置如下：在节点1规划火力发电厂，并作为系统的平衡节点；在节点8接入光伏；将节点25作为风力发电节点。系统节点电压允许范围为0.90～1.05 p.u.。在系统中其余节点规划储能电站，容量和位置待配置。

精准对接建设交通强国的内涵框架，按照全省建设交通强省的战略部署，四川水运将重点在增强供给能力、优化服务质量、强化安全保障、提升管理效率四个方面发力，推动水运实现高质量发展。

正是因为环保的自觉遵守，以及理念超前，所以无锡工厂自2012年起连年被无锡新区评为绿标企业。爱克发用行动证明了印刷业完全可以成为绿色环保产业。

3.1 仿真条件

本文以我国西部某地区光伏发电场和风电场日出力特性分别作为节点8和节点25的输入功率。光伏在10∶00—16∶00 发电功率较强，而风力发电功率随风速变化，如图6所示。

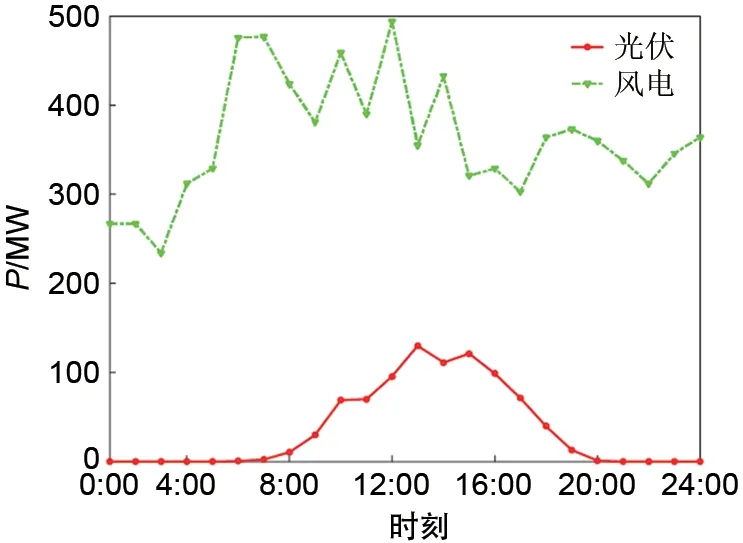
系统总装机容量为2000 MW，风电场总装机容量800 MW，光伏装机容量200 MW，火电机组容量为500 MW，储能类型为容量型化学储能，磷酸铁锂电池。储能系统的相关参数如表3所示。

维纳滤波语音增强技术能有效改善语音质量,抑制带噪语音中的噪声,但和大部分语音增强算法一样,它并不能有效提高语音可懂度(Speech Intelligibility)。维纳滤波算法增益函数依赖于语音各频点的估计信噪比,大量的研究工作用于分析信噪比估计算法的性能对提升语音质量和减少残留噪声的影响,而忽略了分析信噪比估计误差对语音可懂度的影响。而助听器的主要目的是提高使用者的语音可懂度,因此对增强算法的研究需充分考虑增强算法对语音可懂度的影响。

3.2 仿真结果分析

根据权重自适应的WOA算法，各节点配置储能的目标函数值与年运行成本如图7所示。当以火电厂功率波动最低为目标，储能选址在13节点，功率波动6.3 MW，相应储能的配置容量为40.2 MWh，此时的年运行成本为1329 万元。此条件下虽然目标函数最小，但储能容量和年运行成本并非最低值。储能容量配置最低值在2 节点，为27.6 MWh，但此时功率波动达到了12.3 MW，年运行成本也达到了1708万元，两项指标均高于节点13选址。储能年运行成本最低值在24节点，为1001万元，但此时功率波动达到了9.7 MW。

以图6的典型日特性估算年运行特性，储能系统的运行成本为1329 万元。根据行业经验数据，容量型电化学储能技术中经济性较好的是铅蓄电池和磷酸铁锂电池，目前每度电成本大致在0.6～0.9元/kWh

。基于以上数据，假设平均每天完成一次完整的充放电，该储能电站的年运行成本约为880万元～1320万元；若平均每天完成两次完整的充放电，该储能电站的年运行成本约为1760 万元～2640万元；1329 万元位于上述区间内，说明算法得到的运行成本比较合理。

图8 所示为储能系统的出力特性趋势，功率为正表示电池充电，功率为负表示电池放电。储能充电的最大充电功率为50.3 MW，最大放电功率为-48.2 MW，SOC 由最初的60%，变为最终的42%。

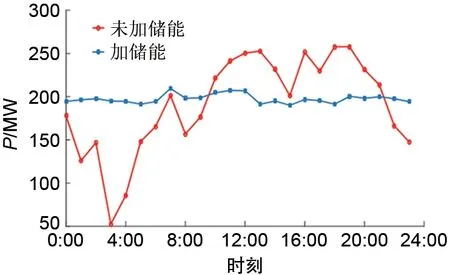
图9所示为在节点13配置储能电站前后，火电厂1的出力曲线。通过对比看出，火电厂的功率波动明显得到改善。未加储能时，在考察时间段内，火电功率的平均值为190.1 MW，最大功率256.7 MW，最小功率53.5 MW，峰谷差达到203.2 MW；加入储能后，火电功率的平均值为195.6 MW，最大功率208.9 MW，最小功率190.1 MW，峰谷差降为18.7 MW。峰谷差减小了90.79%，辅助调峰效果明显。配置储能前后的风火互补系统的功率对比如表4所示。

防污剂在溶胀聚合物中扩散的模拟研究 程栋材,黄志雄,任润桃,王晶晶,叶章基,张亮,王跃平(11-18)

4 结 论

本文基于权重自适应鲸鱼优化算法，提出了多能系统储能电站最优配置方法，研究结果表明：

（1）引入非线性自适应权重

和

对包围猎物、气泡攻击及搜索猎物过程进行改进，通过标准测试函数验证，证明WWOA 相比标准WOA 和GA算法具有更好的收敛速度、求解精度、稳定性以及全局搜索能力，利于求解储能配置目标函数这一非线性规划问题。

（2）利用IEEE33节点系统作为风-光-火-储系统的仿真模型，根据权重自适应鲸鱼优化算法的计算结果，以火电厂的输出功率波动最小作为目标函数，储能选址在13 节点，储能的最优配置容量为40.2 MWh，此条件下储能系统的年运行成本为1329万元。

（3）储能配置策略有效抑制了多能系统中火电厂的功率波动，加入储能后，在平均输出功率基本不变的前提下，火电厂功率的峰谷差由203.2 MW减小为18.7 MW，下降了90.79%，有效实现了辅助调峰。

[1] 陈海生, 刘畅, 徐玉杰, 等. 储能在碳达峰碳中和目标下的战略地位和作用[J].储能科学与技术,2021,10(5):1477-1485.CHEN H S, LIU C, XU Y J, et al. The strategic position and role of energy storage under the goal of carbon peak and carbon neutrality[J]. Energy Storage Science and Technology, 2021, 10(5):1477-1485.

[2] 祁乐, 陈标, 江平, 等. 燃煤火电机组提供调峰辅助服务的成本和效益分析[J].电力大数据,2019,22(10):23-29.QI L, CHEN B, JIANG P, et al. Cost and benefit analysis of peak regulation auxiliary services for coal-fired thermal power units[J].Power Systems and Big Data,2019,22(10):23-29.

[3] 刘英军,刘亚奇,张华良,等.我国储能政策分析与建议[J].储能科学与技术,2021,10(4):1463-1473.LIU Y J, LIU Y Q, ZHANG H L, et al. Energy storage policy analysis and suggestions in China[J]. Energy Storage Science and Technology,2021,10(4):1463-1473.

[4] 张军,张伟,曹凌捷,等.国内储能市场发展现状及趋势分析[J].电力与能源,2020,41(6):739-743.ZHANG J, ZHANG W, CAO L J, et al.Analysis of the development of energy storage market and the key development direction in China[J].Power&Energy,2020,41(6):739-743.

[5] 李建林,李雅欣,周喜超,等.储能商业化应用政策解析[J].电力系统保护与控制,2020,48(19):168-178.LI J L, LI Y X, ZHOU X C, et al.Analysis of energy storage policy in commercial application[J]. Power System Protection and Control,2020,48(19):168-178.

[6] 杨立滨, 曹阳, 魏韡, 等. 计及风电不确定性和弃风率约束的风电场储能容量配置方法[J].电力系统自动化,2020,44(16):45-52.YANG L B, CAO Y, WEI W, et al. Configuration method of energy storage for wind farms considering wind power uncertainty and wind curtailment constraint[J].Automation of Electric Power Systems,2020,44(16):45-52.

[7] 马速良, 蒋小平, 马会萌, 等. 平抑风电波动的混合储能系统的容量配置[J].电力系统保护与控制,2014,42(8):108-114.MA S L, JIANG X P, MA H M, et al. Capacity configuration of the hybrid energy storage system for wind power smoothing[J].Power System Protection and Control,2014,42(8):108-114.

[8] 李建林,郭斌琪,牛萌,等.风光储系统储能容量优化配置策略[J].电工技术学报,2018,33(6):1189-1196.LI J L, GUO B Q, NIU M, et al. Optimal configuration strategy of energy storage capacity in wind/PV/storage hybrid system[J].Transactions of China Electrotechnical Society, 2018, 33(6):1189-1196.

[9] 吴小刚, 刘宗歧, 田立亭, 等. 基于改进多目标粒子群算法的配电网储能选址定容[J].电网技术,2014,38(12):3405-3411.WU X G, LIU Z Q,TIAN L T, et al. Energy storage device locating and sizing for distribution network based on improved multiobjective particle swarm optimizer[J]. Power System Technology,2014,38(12):3405-3411.

[10]艾欣, 李一铮, 王坤宇, 等. 基于混沌模拟退火粒子群优化算法的电动汽车充电站选址与定容[J].电力自动化设备,2018,38(9):9-14.AI X, LI Y Z, WANG K Y, et al. Locating and sizing of electric vehicle charging station based on chaotic simulated annealing particle swarm optimization algorithm[J]. Electric Power Automation Equipment,2018,38(9):9-14.

[11]丁倩,曾平良,孙轶恺,等.一种考虑可再生能源不确定性的分布式储能电站选址定容规划方法[J].储能科学与技术,2020,9(1):162-169.DING Q, ZENG P L, SUN Y K, et al. A planning method for the placement and sizing of distributed energy storage system considering the uncertainty of renewable energy sources[J]. Energy Storage Science and Technology,2020,9(1):162-169.

[12]PANDŽIĆ H, WANG Y S, QIU T, et al. Near-optimal method for siting and sizing of distributed storage in a transmission network[J].IEEE Transactions on Power Systems,2014,30(5):2288-2300.

[13]MASSUCCO S, PONGIGLIONE P, SILVESTRO F, et al. Siting and sizing of energy storage systems: Towards a unified approach for transmission and distribution system operators for reserve provision and grid support[J]. Electric Power Systems Research,2021,190:106660.

[14]BABACAN O, TORRE W, KLEISSL J. Siting and sizing of distributed energy storage to mitigate voltage impact by solar PV in distribution systems[J].Solar Energy,2017,146:199-208.

[15]李昀昊, 王建学, 曹晓宇, 等. 面向风电场-储能-输电网联合规划的机会约束IGDT模型[J].电网技术,2019,43(10):3715-3724.LI Y H, WANG J X, CAO X Y, et al. A chance-constrained IGDT model for joint planning of wind farm, energy storage and transmission[J].Power System Technology,2019,43(10):3715-3724.

[16]肖浩, 裴玮, 杨艳红, 等. 计及电池寿命和经济运行的微电网储能容量优化[J].高电压技术,2015,41(10):3256-3265.XIAO H, PEI W, YANG Y H, et al. Energy storage capacity optimization for microgrid considering battery life and economic operation[J].High Voltage Engineering,2015,41(10):3256-3265.

[17]李益民, 王关平, 马建立, 等. 基于天牛须搜索遗传算法的风光柴储互补发电系统容量优化配置研究[J]. 储能科学与技术, 2020, 9(3):918-926.LI Y M, WANG G P, MA J L, et al. Study on optimal capacity in the construction of wind-solar-dieselbattery hybrid power system based on bettle antennae search algorithm improved genetic algorithm[J].Energy Storage Science and Technology,2020, 9(3):918-926.

[18]袁晓玲, 程淋伟, 鲁丽娟, 等. 基于万有引力搜索算法的微电网风光储容量优化配置[J].电力需求侧管理,2017,19(6):14-19.YUAN X L, CHENG L W, LU L J, et al. Configuration optimization of wind-solar-storage system in microgrid based on GSA[J].Power Demand Side Management,2017,19(6):14-19.

[19]赵晶,祝锡晶,孟小玲,吴霄.改进鲸鱼优化算法在机械臂时间最优轨迹规划的应用[J/OL]. 机械科学与技术:1-10[2022-06-20].DOI:10.13433/j.cnki.1003-8728.20200596.

[20]赵传武, 黄宝柱, 阎跃观, 等. 一种非线性权重的自适应鲸鱼优化算法[J].计算机技术与发展,2020,30(10):7-13.ZHAO C W, HUANG B Z, YAN Y G, et al. An adaptive whale optimization algorithm of nonlinear inertia weight[J]. Computer Technology and Development,2020,30(10):7-13.

[21]何颖源,陈永翀,刘勇,等.储能的度电成本和里程成本分析[J].电工电能新技术,2019,38(9):1-10.HE Y Y, CHEN Y C, LIU Y, et al.Analysis of cost per kilowatt-hour and cost per mileage for energy storage technologies[J].Advanced Technology of Electrical Engineering and Energy,2019,38(9):1-10.