基于优化Elman神经网络的锂电池容量预测

为了缓解能源短缺、环境危机和空气污染等问题，电动车被大力发展和广泛应用。锂电池由于具有能量密度大、体积小、无记忆效应、自放电率低等优点而被作为电动汽车的主要动力源

。通常，锂电池的性能和安全性会随着电池容量的衰退而逐渐降低，当锂电池的容量衰退到额定容量的80%时就不再适合做动力电池，而需要及时更换

。因此，为保障锂电池安全可靠地运行，需要发展先进的技术和相关算法来对锂电池的容量进行准确的预测，让用户能够在电池失效之前及时进行维护和更换

。

目前，电池容量的预测方法一般分为模型驱动方法和数据驱动方法

。基于模型驱动的方法主要根据电池的衰退机理建立等效电路模型然后结合先进的滤波技术进行容量预测。为解决锂离子电池容量预测不准确的问题，文献[6]开发了一个用于电池容量预测的贝叶斯学习框架，基于电化学阻抗谱(electrochemical impedance spectrum，EIS)中的特征构建老化模型，并利用粒子滤波算法(particle filter，PF)更新模型参数和预测电池容量。文献[7]研究了不同使用条件和环境温度下的电池退化模型，提出了一种基于球形容积法改进的PF 模型的电池容量预测方法。文献[8]采用容积卡尔曼滤波(cubage kalman filter，CKF)和经验拟合的方法来估计锂电池的容量。文献[9]研究了电池在不同使用条件和环境温度下的退化建模，进一步提出了一种朴素贝叶斯模型，用于预测不同工况下电池的容量。虽然模型驱动的方法有明确的物理意义，但是需要分析电池内部反应并进行大量复杂参数计算才能建立起准确的模型，因此不适合实时监测，而是更多地用于理论研究和电池设计上，这严重限制了模型驱动方法的一般适用性。

数据驱动的方法不需要精确分析电池内部系统的机理和化学反应，而是使用传感器测量到的电池运行数据，提取其中有效的老化特征，并采用机器学习方法预测电池容量

。文献[11]提出一种基于先验知识的神经网络和马尔科夫链的电池容量预测模型。利用内核技术，支持向量机(support vector machine，SVM)

和高斯过程回归(gaussian process regression，GPR)

展示了优越的容量预测性能。文献[14]提出了一种基于蚁群算法优化的BP神经网络的锂离子电池容量衰退预测方法。文献[15]提出了一种基于充电健康特征提取的锂电池容量预测的数据驱动方法。该方法中基于充电数据提取了14 个健康特征，并用主成分分析法进行优化，然后用关联向量机(relevance vector machine，RVM)实现了容量的预测。文献[16]基于锂电池的部分充电数据，提出了一个融合扩展卡尔曼滤波和高斯过程回归的方法进行容量在线预测。文献[17]从部分增量容量曲线中提取相关特征向量，然后分别用高斯过程回归模型和自回归模型实现了短期电池状态的健康评估和长期电池容量的预测。文献[18]提出一个融合Elman神经网络和LSTM神经网络的方法来进行容量预测，Elman神经网络和LSTM神经网络分别用来预测容量退化数据的高频和低频层面。不过Elman神经网络收敛速度较慢，还可能会陷入局部最小值，从而会影响预测精度和运算效率。

为了解决采用数据驱动方法难以获得高效特征量和传统Elman神经网络预测算法预测精度不高以及运算效率低的问题，本工作基于电池老化数据特征与GA-Elman神经网络进行了对锂电池容量的预测，在保证精度的同时提高了预测效率。首先，对所获得的数据集进行特征选择和处理，之后进一步采用主成分分析算法(principal component analysis，PCA)降低数据的维度和复杂度以提高预测效率，然后利用GA-Elman 神经网络建立容量预测模型，以此最终实现对锂离子电池容量的高效准确预测。

1 电池老化实验及数据

本工作中，4 个锂离子电池的循环老化数据均来自于

中的开源数据

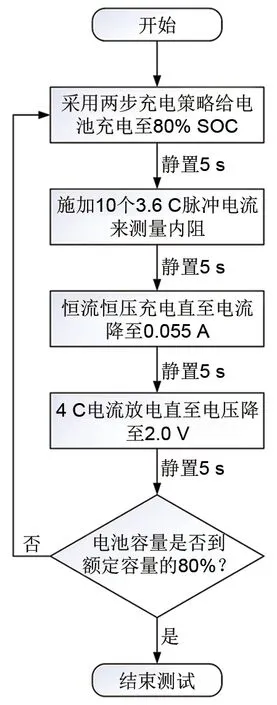
，这些数据都是通过商用磷酸铁锂/石墨电池的循环寿命试验获得。测试电池的额定容量均为1.1 Ah，额定电压为3.3 V，其详细规格如表1所示。电池寿命实验的详细流程如图1所示。测试电池均被放置在30 ℃的热控制室中，由Arbin电池测试设备进行循环实验。该实验采用两步快速充电策略对电池进行充电，充电至电池的80% SOC；再由10 个3.6 C 脉冲电流，每个脉冲持续33 ms，以实现内阻测量，其中C为额定容量；之后以恒流恒压充电直至电流降至0.055 A，最后由4 C 电流放电直至下截止电压2.0 V，最后反复循环整个流程直至电池容量衰退到额定容量的80%。此外，实验中，还通过电池表面的T-型热电偶对电池表面温度进行了测量。

The first time I met Zhu Bing Ren was during an exhibition of his works in Beijing. I was a little confused by the variety of works he showed.

2 容量预测实现方案

2.1 老化特征提取

为了更好地反映充放电过程中电池电特性随循环次数增加的变化规律，本工作采用容量增量法对其恒流放电过程数据进行了处理。随着电池容量的衰退，恒流放电阶段容量增量(discharge incremental capacity，DIC)曲线的峰值变化是有效表征锂电池内部理化特性的状态量

，DIC 曲线定义为放电容量与电压的微分，如式(1)所示。

式中，

V

代表

时刻的电池端电压。在恒流放电模式下，电流为恒定值，当取极小的时间间隔∆

时，公式(1)是成立的，由此可以绘制出恒流放电阶段的DIC曲线。由于本工作是大电流情况下提取DIC特征，大电流会抹除部分DIC曲线特征，比如某些波峰的消失，导致从低电流的多波峰特征变化成大电流下的单波峰特征，因此本工作只提取了单波峰的特征。不同循环下的DIC 曲线如图3 所示，为直观表示DIC峰值特征随循环数的变化，进一步分别将DIC峰值往

轴面和

轴面上投影，可以得到DIC峰值及DIC峰值对应电压值的变化趋势。由图3可知DIC峰值对应电压会随着循环次数的增加而下降，而DIC 峰值会上升，表明不同循环下的DIC曲线呈现明显的峰值特征。

在电池老化过程中，会伴随着电特性和热特性的改变，其热特性的变化主要是由电池老化导致的内阻增加以及由内阻增加导致的电池充放电温升加大，所以有必要引入平均温度和内阻作为模型的两个输入特征量，从而让预测模型能从多特征量中学习到更多的电池老化信息。实际情况下，可以通过卡尔曼滤波或者递推最小二乘法来获得内阻。因此可以选择经过滤波处理后的DIC峰值、DIC峰值对应的电压值、内阻以及温度这四个变量作为电池的老化特征。为进一步宏观分析这四个特征量在电池容量衰退以及循环数增加过程中的变化规律，提取不同循环下对应的四个特征量的值作三维颜色图，如图4 所示。图4 的

、

轴分别表示循环数和容量，其中，图4(a)的

轴表示DIC峰值，颜色栏表示DIC 峰值对应电压值，图4(b)的

轴表示内阻，颜色栏表示温度。从图4(a)中可以直观看到，随着循环数的增加和电池容量的衰退，

轴数值在增大，颜色逐渐由深红到浅黄，这表明随着循环数的增加DIC峰值增大而DIC峰值对应的电压值逐渐减小；由图4(b)可以得到，随着循环数的增加和电池容量的衰退，

轴数值在增加，颜色由蓝变红再变蓝，这表明温度会出现波动性的变化，内阻也会增加。因此可以选择经滤波处理后的DIC 峰值、DIC峰值对应的电压值、内阻以及温度这四个变量作为电池的老化特征，分别简化表示为

1、

2、

3和

4。

图5为循环数和DIC峰值及其对应电压值的关系曲线，该结果进一步验证了老化特征量

1、

2与容量衰退的关联关系。从图5(a)和(b)中可以看出，在电池容量衰退到额定容量的90%以下时，DIC峰值绝对值及其对应电压值会急剧下降，这和电池容量的衰退规律近似，因此可将

1和

2作为电池容量衰退预测模型的老化特征输入量。

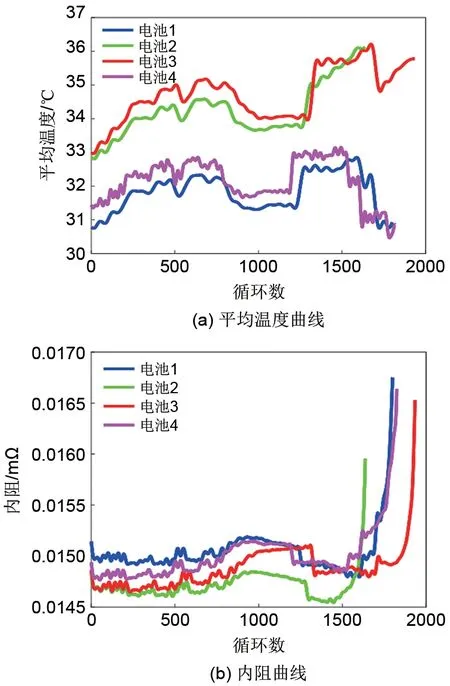
此外，为了进一步研究电池老化过程中特征量

3和

4随循环数的变化规律，得到了内阻和温度随着循环数的具体变化关系如图6所示。图6(a)绘制了电池1～4 每个循环的平均温度变化，从图中可以看出前1500 个循环四个电池数据的温度在整体趋势上变化很类似，都是上升的趋势，这是因为同类电池表现的特征是相同的，这和电池老化导致的温升规律相似。从图6(b)中可知，内阻在电池老化过程中会逐渐升高，且在电池容量衰退到额定容量的90%以下时，内阻会急剧增加，进一步表明可以将

3和

4作为电池容量衰退预测模型的老化特征输入量。

2.2 基于GRA的老化特征分析

例1：Westminster car crash:Man arrested on suspicion of terror offences(BBC,Aug.15,2018)威斯敏斯特汽车撞车案：男子涉嫌恐怖袭击被捕

关联系数

的具体表达式如式(2)所示

反思是教师发展的重要基础。是否具有反思的意识和能力，是区别作为技术人员的经验型教师与作为研究人员的学者型教师的主要指标之一。真正的成长在实践后，不会反思、总结、提炼，多少实践都不会带来巨大的进步。反思，是指行为主体立足于自我以外批判地考察自己行为的能力。班主任的反思是指班主任在带班育人实践中,以自我行为表现及行为为依据的“异位”解析和修正,进而不断提高自身教育管理效能和素养的过程。

式中，

称为分辨系数，取值在0～1，文中取值为0.5；

表示特征量；

为循环次数；

x

(

)和

x

(

)分别是需要计算关联度的变量。通过GRA 分析，得到了四个老化特征量与每个电池容量之间的相关强度，即

值，各个老化特征量与对应电池容量的相关强度如表2 所示。相关强度

值处于0～0.2则表示相关性非常弱或没有相关性，处于0.8～1.0 表示相关性非常强。从表2 中可以看出，四个老化特征量

1、

2、

3、

4与容量的灰色关联度值都大于0.6，证明四个特征量与容量之间存在比较强的相关性，这表明引入多个老化特征量是可行的。且四个电池的老化特征量

1的

值都大于0.9，这表明

1 与容量之间具有非常强的相关性。通过上述分析，可以得到所选取的四个老化特征量对于电池容量的预测是很有效的。

2.3 特征降维

电池管理系统(battery management system，BMS)处理数据过程中，如果数据量过于庞大，则会占用大量车载运算模块的计算能力，从而影响整体性能。此外，通过PCA 降维，还能部分去除数据噪声，提高模型输入特征数据的质量。因此本工作采用PCA算法对老化特征数据集进行降维处理，从而将高维度的特征量数据降维，以减少BMS 处理的数据量，节约储存空间，进一步加快计算速度，满足实时预测的需求。PCA算法是一种基于变量协方差矩阵对数据进行压缩降维、去噪的算法

，利用正交变换把一系列可能线性相关的变量转换为一组线性不相关的变量，转换后的这组变量就称为主成分，从而能在减少矩阵维度的同时尽可能地保留原矩阵的主要特性而不丢失原矩阵的主要特征。PCA算法对高维数据进行低维降维分为以下几个步骤

最后，还需要建立跨境基础设施债券市场、跨境基础设施交易平台及其他跨境基础设施投融资平台，这样才能充分发挥和放大亚投行对“一带一路”倡议的支撑作用。总之，亚投行的发展建设不能局限于一点或一隅，而是一项系统性的工程设计。

不同的金属盐溶液对应腐蚀不同的金属版，如铜版用硫酸铜、锌版用硫酸锌等。这种方法不产生气体，安全性也很高：工作的直流电电压通常不超过20V，处于安全电压（36V）范围，金属盐溶液腐蚀性非常低。同时，腐蚀过程不会消耗硫酸铜，溶液可反复使用，经济性非常高。

③创建适应度函数。在遗传算法进化搜索中，适应度用来衡量种群中每个个体可能达到最优解的程度。适应度值越高，个体遗传给下一代的概率就越大。本工作的优化目标是使Elman神经网络的输出值与期望值之间的误差最小。因此，取输出值与期望值误差平方和的倒数作为适应度函数，适应度函数如式(7)所示

（2）计算样本的协方差矩阵

，得到其特征值和特征向量；

据知情人回忆，黎永兰的教学成绩优异，她所带班级在广安名列前茅。2003年，黎永兰参加了公务员考试，告别讲台成为一名公务员，先后在广安大有乡、龙台镇等地担任了副乡长、镇长等职务，“工作很有一套”。

（3）对协方差矩阵

进行特征值分解；

（4）将特征值从大到小排序，取出最大的

个特征值所对应的特征向量(

...

ω

)，将所有取出后的特征向量进行标准化，组成特征向量矩阵

；

在上述方法的基础上，为了适应电动汽车车载BMS 的在线容量预测需求，进一步提出了大数据平台的在线容量预测框架。图8(b)为基于离线模型建立和在线容量预测的框架流程图。它包括两个部分：预测模型参数的离线辨识和在线应用。在离线模型建立部分，通过实验室测试的数据对该类型电池进行离线模型建立和训练，即模型是通过离线实验数据建立、训练和测试的。通过训练集数据自适应生成GA-Elman神经网络模型，之后再用测试集数据检验模型的预测精度和计算效率。在线容量估计部分，通过离线状态下将训练好的模型植入在线容量预测部分，通过输入车载获得的老化实时特征数据，对电池容量进行在线预测。

为了进一步确定各个老化特征量与容量衰退的具体关联系数，本工作采用灰色关联度分析(gray relation analysis，GRA)法来评价四个老化特征量与电池容量的相关性。GRA 是基于灰色系统理论的一种多因素统计分析方法，它根据因素之间发展趋势或者变化趋势的相似性和差异性来评价因素之间的关系等级。采用GRA 的目的是通过研究几何接近度来评价不同曲线之间的关系，接近度越高，相关性越强。通过定量分析，突出了参考序列和比较序列之间的相似性和差异性，基于GRA 的定量分析是为了获得参考序列和比较序列之间的相关性

。

2.4 基于GA-Elman 神经网络的容量预测模型构建

2.4.1 Elman神经网络

（2） 首先检查 SDH电源是否故障，如果有即修复电源，修复后SDH若无告警则流程转入第（4）步。若SDH告警为次要告警，则流程转入第（3）步。若为主要告警，先对两端SDH在ODF处自环，若告警不消除，则需要对ODF和SDH排查和检修，ODF检修为更换尾纤或光接头，SDH检修则为找出故障板卡并更换。若无主要告警，环回方式改成如下，在其中一端 ODF处环回给对端，观察对端是否有主要告警，若有告警即可诊断为光链路或中继 SDH故障，需要参考专用保护通道故障定位处理方法解决故障，并消除中继SDH故障。

Elman神经网络本质上是一种全局前馈局部递归网络，它在前馈式网络的隐藏层中增加了一个承接层，作为一步延时的算子，以达到记忆的目的

。Elman神经网络是一种具有反馈功能的BP神经网络，除了具有BP 神经网络的基本功能之外还具有短时记忆功能。它可以看作是具有局部记忆单元和局部反馈连接的递归神经网络，具有与多层前向网络相似的多层结构。Elman神经网络的结构如图7所示。与前馈神经网络相比，Elman神经网络具有更强的计算性能，可用于解决快速优化问题。此外，它还能以理想的精度逼近任意非线性关系，具有更高的计算性能

。由于锂电池具有微小容量再生特性，利用Elman神经网络预测锂电池容量时，网络的隐含层可以访问电池前一循环的历史数据，这可以适应锂离子电池的这一特性。

Elman神经网络的非线性状态空间函数可表示为式(4)所示

式中，

为输出层的

维向量，

为

维中间层向量，

为输入层的

维向量，

为

维反馈状态向量。

ω

、

ω

、

ω

分别为输入层、连接层和输出层对应的权值矩阵。

(*)为输出层神经元的传递函数，

(*)为连接层神经元的传递函数，通常用

函数表示，如式(5)所示

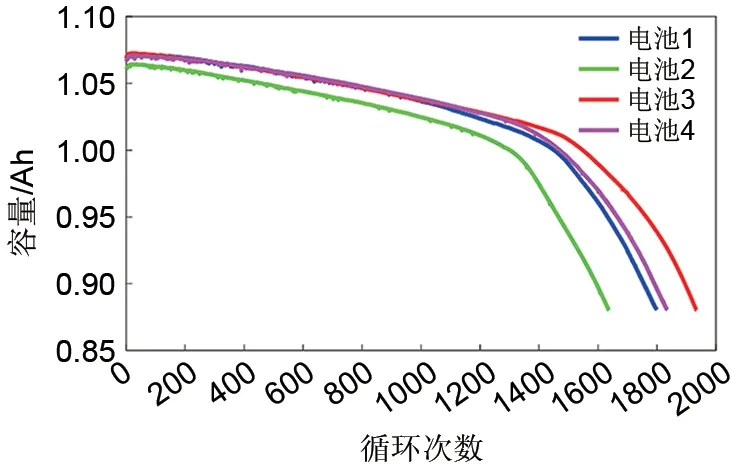
4 个电池的容量衰退曲线如图2 所示，从图2中可以看出，测试电池的容量衰退趋势基本相同，这说明同一类型锂离子电池在类似使用条件下的寿命老化机理基本一致；在电池容量大于1 Ah(额定容量的90%)时，4个电池的衰退速率均较慢，而当电池容量小于1 Ah时，4个电池的衰退速率就会激增。这表明电池的某些老化特征以90%电池额定容量为临界点，在小于90%电池额定容量时发生了剧烈的变化。在电池循环老化过程中，其电特性和热特性也会随着电池的老化而发生变化。接下来，本工作将从电池的电特性和热特性等这些变化中提取与电池容量退化有关的老化特征量。

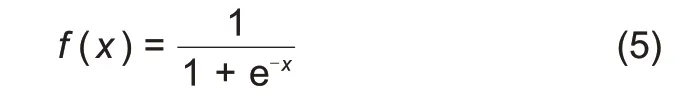
采用误差平方和作为学习指标，计算出训练样本的总误差准则函数如式(6)所示

由表1可以看出，构建的石油安全评价指标体系包含5个一级评价指标和15个二级评价指标。将石油安全程度设置为目标层A，将石油供给安全、消费安全、贸易安全、地缘政治安全及生态安全5个一级指标设为R，将直接影响一级指标的15个二级指标设为X。

④进行选择、交叉、变异等遗传操作，寻找最优模型参数。计算出最优适应度个体并进行重复遗传迭代，剔除最坏适应度个体。经过迭代和进化，当得到种群遗传代数集时，就可以得到Elman网络的最优权值和阈值。

本研究主要探讨HBO治疗对SNFH中期的保护作用，研究通过交叉对照试验，比较组内及组间HBO治疗之后的差异，发现HBO治疗可以改善SNFH中期的Harris评分、骨髓内的水肿程度以及提高SNFH中期患者的疼痛缓解有效率，但是不能改变股骨头坏死指数、股骨头坏死面积。这提示HBO治疗对于改善SNFH中期(ARCOⅡa～Ⅲa期)的临床症状及骨髓水肿程度具有一定的临床价值，但是HBO治疗无法改善SNFH中期已经出现的股骨头坏死，无法逆转病情。

传统的Elman神经网络以梯度下降法作为权值更新方法。当该方法的误差函数有多个局部最小值时，它就很难保证找到最优解，并很容易陷入局部最小值，从而导致收敛速度慢，也会影响网络训练效果，降低结果精度

。为了解决这一问题，本工作采用具有全局搜索能力的遗传算法对Elman神经网络进行优化，优化了Elman神经网络的权值和阈值，提高算法的预测精度和运算效率。完成特征处理后，本工作采用GA-Elman神经网络开展了锂电池容量预测模型的构建。GA-Elman 神经网络模型的构建思路如图8(a)所示，具体优化步骤如下:

①确定Elman神经网络的隐藏层神经元数量及其他相关网络参数；

②生成初始种群。网络的权值和阈值用实数编码，将实数视为染色体或个体，多个个体构成一个种群；

回程在苏州，时已秋转冬，天气沁凉。晚上穿单衣找到个卖烤串的羊肉汤店，边抱怨天气凉得快边要了个葱段覆盖萝卜和羊肉的砂锅，一锅下去，觉得全身滚烫，寒意全都化作白气，冒到一佛升天。立刻觉得：“嗯，夜宵的感觉回来了。”

（1）对输入

维样本集

=[ ]

...

中的所有样本进行中心化：

由此可见，财务会计在保障企业经济收益方面发挥着非常重要的作用。供水企业为了保障自身的经济效益，并且获得长期可持续的发展，就应该加强财务会计管理工作，通过改变老旧的管理理念，不断顺应变化的市场环境的需求。并且还应该对资金进行合理的安排，同时也确保资金的使用合理有效，以此来实现增值企业资产的目的。

由表中结果可知，灼烧样品时间大于40 min后烧失量的测定结果与样品反复灼烧所测得的结果相差很小，因而为了节约时间和成本，试验操作时可以灼烧样品40 min左右进行结果测定。

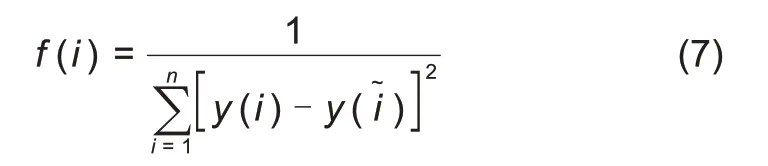
2.4.2 GA-Elman神经网络容量预测模型构建

⑤将遗传算法优化后得到的最优权值和阈值转移到Elman神经网络中，进行网络训练。重复步骤②～⑤，当达到网络训练迭代集的终止条件时，结束循环。

（5）对样本集中的每一个样本

，投影到所选取的特征向量(

...

ω

)上，转化为新的样本

=

；

3 结果与讨论

3.1 容量预测模型的评价指标

为了评估所建立的GA-Elman神经网络模型的容量预测精度，采用相对误差

、平均绝对误差(maximum absolute error，MAE)、均 方 根 误 差(root mean square error，RMSE)和拟合度

来评估模型的预测效果

。

、MAE、RMSE 和

的计算公式如式(8)～(11)所示

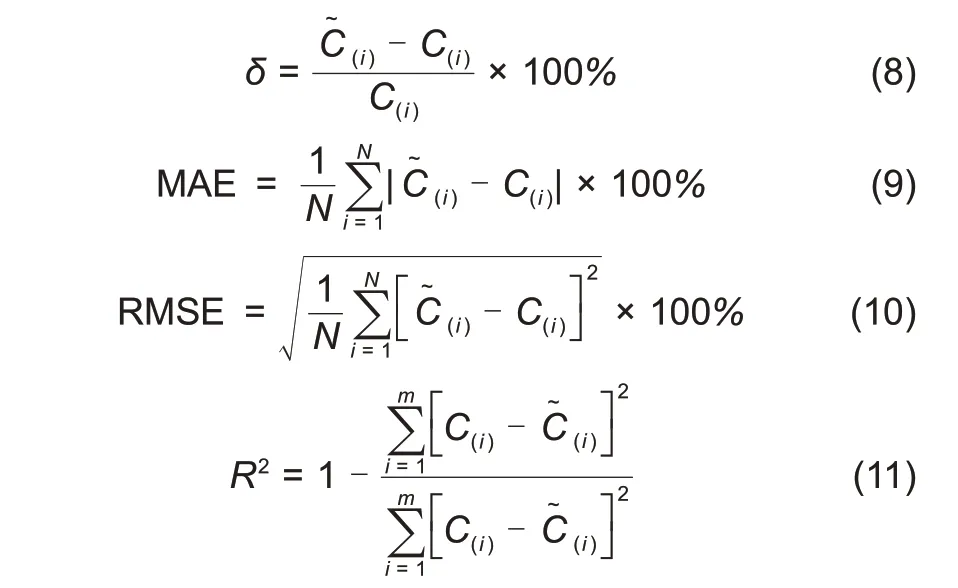
3.2 模型预测结果

（1）不同训练量对结果的影响

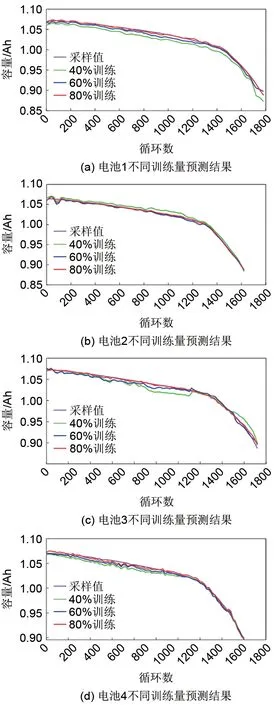
为提高网络的学习速度及预测精度，将降维后的特征向量进行归一化处理之后作为GA-Elman神经网络的输入值，模型输出值为预测的电池容量。在数据驱动方法的实现过程中，训练数据量需要根据模型复杂程度、获取训练数据的难易程度以及误差容忍度来确定。首先根据模型复杂程度，分别划分每组数据中的40%、60%、80%作为训练集，剩余的数据量作为测试集。输入网络模型后，不同训练量下模型的训练测试结果如图9所示，分别采用平均绝对误差(MAE)、均方误差(MSE)和均方根误差(RMSE)对模型预测部分的效果进行分析，如表3所示。

由图9 中可以看到，当训练数据量为80%时，模型的预测精度最高，模型整体的预测跟踪效果很好，模型的预测值几乎与采样值吻合，且最大RMSE 仅为0.57%；当模型的训练量降低至60%时，模型的预测精度只是略微地降低，模型整体的预测跟踪效果稍微下降，不过依然可以保持很好的预测跟踪效果，所有预测结果中最大MAE 为0.35%，最小

为0.971，最大RMSE 为0.93%。不过当训练数据量减少至40%时，模型的估算精度则较低，特别是循环数前中期的预测跟踪效果相对较差，预测结果的最大MAE为1.2%，最小

为0.933，最大RMSE 为1.97%。从以上三组不同训练量的预测效果来看，60%训练数据下的预测精度与80%训练数据下的预测精度结果相差无几，而40%的预测精度就相对较低。考虑到预测精度和模型训练成本，本工作选择60%的数据作为预测模型的训练集输入量。

很多学生进入大学后会松懈，喜欢游戏、娱乐，荒废了学习。很多学生形成了一种懒惰、消极的生活态度，这种生活态度给管理人员带来了很大的工作障碍。对此，高校管理人员必需要在入学时对学生进行有效管理，从一开始培养学生良好的学习态度，明确学生大学生活的学习目标，提升学生的学习动力。

（2）不同估算方法对比

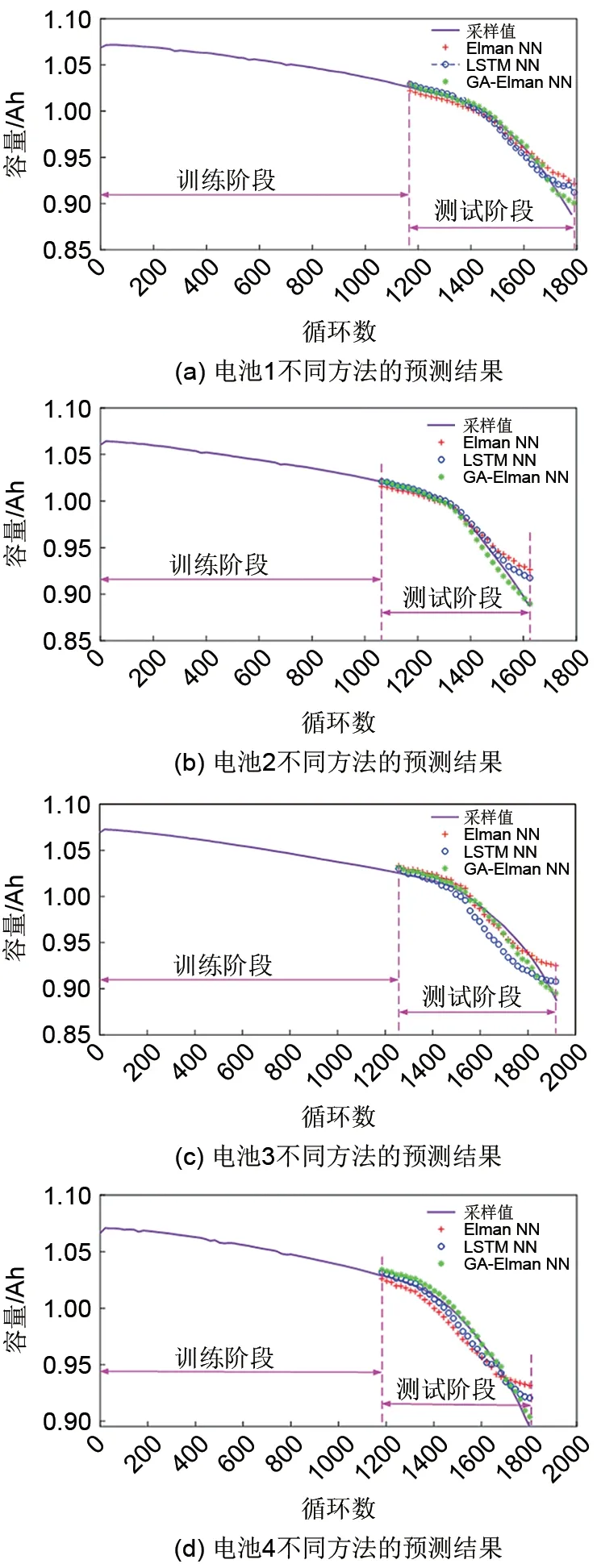
为进一步验证基于特征处理建立的GA-Elman神经网络算法模型在预测精度和运算效率上的优越性，选取60%样本数据量分别作为Elman 神经网络、LSTM 神经网络和GA-Elman 神经网络算法模型的输入训练集，比较三种不同神经网络预测模型的容量预测结果以及预测误差和运算效率，结果如图10和表4所示。

从图10及表4中可以看出，与具有循环结构的Elman神经网络和具有记忆功能的LSTM神经网络相比较，GA-Elman 神经网络对电池1～电池4 的容量预测效果和运算效率均优于LSTM神经网络和Elman 神经网络。Elman 神经网络模型的四个电池预测结果的平均RMSE 为1.38%，平均耗时为13.42 s；LSTM神经网络模型的四个电池预测结果的平均RMSE 为0.89%，平均耗时为21.59 s；而GA-Elman 神经网络模型对4 个电池容量预测结果的平均RMSE为0.5%，平均耗时为10.65 s，两项指标均优于Elman神经网络和LSTM神经网络，这表明在预测精度和运算效率方面，GA-Elman 神经网络预测模型均体现出优越性。此外，在容量衰退预测的前半段，Elman神经网络的预测结果和采样值之间的偏差比较大，而GA-Elman神经网络的预测精度很高，这表明引入遗传算法优化的GAElman神经网络可以避免Elman神经网络容易陷入局部最小值和收敛速度慢的缺点。由于GA-Elman神经网络的预测精度和运算效率方面均要优于传统的Elman神经网络，这就证明传统的Elman神经网络很难保证找到最优解，并很容易陷入局部最小值，从而导致收敛速度慢，也会影响网络训练效果，降低结果精度。

为了进一步从预测效果和运算效率方面证明GA-Elman 可以避免Elman 神经网络存在的融入陷入局部极小值的缺点，以前60%的实验数据作为训练集，后40%的数据作为测试集，神经网络的参数设置均一样，容量预测对比结果如图11和表4所示。Elman神经网络模型的四个电池预测结果的平均RMSE 为1.41%，平均耗时为13.53 s；而GA-Elman 神经网络模型对四个电池容量预测结果的平均RMSE为0.395%，平均耗时为10.59 s，结果表明GA-Elman神经网络的预测精度和计算效率均优于传统Elman 神经网络。这就证明传统的Elman神经网络很难保证找到最优解，并很容易陷入局部最小值，从而导致收敛速度慢，也会影响网络训练效果，降低结果精度。

（3）多电池数据的预测结果对比

为进一步验证基于特征处理所建立的GAElman神经网络预测模型具有良好的适应性，选择电池1全部的老化循环数据作为模型训练数据，将本文提出的预测模型分别应用于预测剩余锂离子电池全寿命周期的容量衰退情况，其容量预测结果、预测误差如图12和表5所示。

从图12中和表5可以得出，三个电池预测结果的相对误差

均不超过3%，且绝大部分相对误差

在2%以内，特别是电池4 的预测结果，其相对误差

都不超过2%，并且绝大部分相对误差

都在1%以内。三个电池预测结果中，预测误差最大的是2号电池，但其MAE仅为0.97%、

为0.9679、RMSE 为1.02%，且其相对误差

都小于3%。这表明GA-Elman神经网络预测模型在锂电池全寿命周期内具有很好的预测效果。

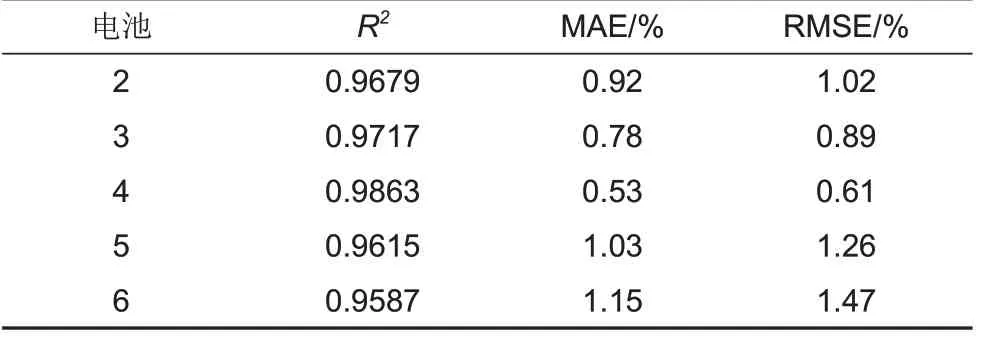
为了进一步验证模型的适应性，我们采用

数据库中的不同工况两个电池的实验室数据进一步地验证和分析，命名为电池5(1155 个循环)和电池6(1158 个循环)，其额定容量为均为1.1 Ah，测试温度为30 ℃。具体充放电过程为：首先在5.6 C 恒定电流条件下进行充电，充电至SOC 为36%，然后进行4.3 C 恒流充电至SOC 为80%，最后电池以1 C 恒流恒压充电至上截止电压3.6 V；然后在4 C恒定电流条件下放电，直到电压降至2.0 V。分别提取3个电池的

、

、

和

以及电池容量数据。利用电池1的数据进行模型训练，并预测电池5 和6 的容量。其结果如图12(g)～(j)及表5所示。分析可知：①电池5和电池6的RMSE分别为1.26%和1.47%，具有较高的精度；②电池5 和电池6 的MAE 为1.03% 和1.15%，

为0.9615 和0.9587，对容量的预测效果理想。这证明该模型对不同工况具有良好的适应性，在不同电池上都表现优异。

4 结 论

本工作基于电池老化特征和优化Elman神经网络算法提出了一种高精度和高效率预测锂电池容量的方法。由老化循环数据中提取4组与容量退化相关的老化特征向量，经过PCA 算法分别对多维特征量进行低维映射，降低特征量数据维度的同时提高了特征值的有效信息量，从而提升了预测效率。在此基础上，利用GA-Elman神经网络建立了容量预测模型。GA-Elman 神经网络模型对4 个电池容量预测结果的平均RMSE 为0.5%，平均耗时为10.65 s，与Elman 神经网络模型和LSTM 神经网络模型相比，预测精度和效率有较大优势。此外，不同工况电池的全寿命周期容量预测验证结果表明，对容量预测结果最大相对误差不到3%，表明该方法对不同电池具有较好的适应性。

[1] CHEN Z, SUN M M, SHU X, et al. Online state of health estimation for lithium-ion batteries based on support vector machine[J].Applied Sciences,2018,8(6):925.

[2] SHU X, LI G, SHEN J W, et al. An adaptive fusion estimation algorithm for state of charge of lithium-ion batteries considering wide operating temperature and degradation[J]. Journal of Power Sources,2020,462:doi:10.1016/j.jpowsour.2020.228132.

[3] HU X S, LI S E, YANG Y Lapproach.Advanced machine learning approach for lithium-ion battery state estimation in electric vehicles[J]. IEEE Transactions on Transportation Electrification,2016,2(2):140-149.

[4] 马彦,陈阳,张帆,等.基于扩展H∞粒子滤波算法的动力电池寿命预测方法[J].机械工程学报,2019,55(20):36-43.MA Y, CHEN Y, ZHANG F, et al. Remaining useful life prediction of power battery based on extend H∞particle filter algorithm[J].Journal of Mechanical Engineering,2019,55(20):36-43.

[5] HU X S, YUAN H, ZOU C F, et al. Co-estimation of state of charge and state of health for lithium-ion batteries based on fractional-order calculus[J]. IEEE Transactions on Vehicular Technology,2018,67(11):10319-10329.

[6] SAHA B, GOEBEL K, POLL S, et al. Prognostics methods for battery health monitoring using a Bayesian framework[J]. IEEE Transactions on Instrumentation and Measurement, 2009, 58(2):291-296.

[7] 韦海燕, 安晶晶, 陈静, 等. 基于改进粒子滤波算法实现锂离子电池RUL预测[J].汽车工程,2019,41(12):1377-1383.WEI H Y, AN J J, CHEN J, et al. RUL prediction of lithium-ion battery based on improved particle filtering algorithm[J].Automotive Engineering,2019,41(12):1377-1383.

[8] 郑涛,张里,侯杨成,等.基于自适应CKF的老化锂电池SOC估计[J].储能科学与技术,2020,9(4):1193-1199.ZHENG T, ZHANG L, HOU Y C, et al. SOC estimation of aging lithium battery based on adaptive CKF[J]. Energy Storage Science and Technology,2020,9(4):1193-1199.

[9] NG S S Y, XING Y J, TSUI K L. A naive Bayes model for robust remaining useful life prediction of lithium-ion battery[J]. Applied Energy,2014,118:114-123.

[10]ZHANG Y Z, XIONG R, HE H W, et al. Lithium-ion battery remaining useful life prediction with box-cox transformation and Monte Carlo simulation[J]. IEEE Transactions on Industrial Electronics,2019,66(2):1585-1597.

[11]DAI H D, ZHAO G C, LIN M Q, et al. A novel estimation method for the state of health of lithium-ion battery using prior knowledgebased neural network and Markov chain[J]. IEEE Transactions on Industrial Electronics,2019,66(10):7706-7716.

[12]DENG Y W, YING H J, ER J Q, et al. Feature parameter extraction and intelligent estimation of the state-of-health of lithium-ion batteries[J].Energy,2019,176:91-102.

[13]韩云飞, 谢佳, 蔡涛, 等. 结合高斯过程回归与特征选择的锂离子电池容量估计方法[J].储能科学与技术,2021,10(4):1432-1438.HAN Y F, XIE J, CAI T, et al. Capacity estimation of lithium-ion batteries based on Gaussian process regression and feature selection[J]. Energy Storage Science and Technology, 2021, 10(4):1432-1438.

[14]张新锋, 姚蒙蒙, 王钟毅, 等. 基于ACO-BP 神经网络的锂离子电池容量衰退预测[J].储能科学与技术,2020,9(1):138-144.ZHANG X F, YAO M M, WANG Z Y, et al. Lithium-ion battery capacity decline prediction based on ant colony optimization BP neural network algorithm[J]. Energy Storage Science and Technology,2020,9(1):138-144.张新锋, 姚蒙蒙, 王钟毅, 等. 基于ACO-BP 神经网络的锂离子电池容量衰退预测[J].储能科学与技术,2020(1):173-179.ZHANG X F, YAO M M, WANG Z Y, et al. Lithium-ion battery capacity decline prediction based on ant colony optimization BP neural network algorithm[J]. Energy Storage Science and Technology,2020(1):173-179.

[15]GUO P Y, CHENG Z, YANG L. A data-driven remaining capacity estimation approach for lithium-ion batteries based on charging health feature extraction[J]. Journal of Power Sources, 2019,412:442-450.

[16]ZHOU D, YIN H T, XIE W, et al. Research on online capacity estimation of power battery based on EKF-GPR model[J].Journal of Chemistry,2019:doi:10.1155/2019/5327319.

[17]LI X Y, WANG Z P, YAN J Y. Prognostic health condition for lithium battery using the partial incremental capacity and Gaussian process regression[J].Journal of Power Sources,2019,421:56-67.

[18]LI X Y, ZHANG L, WANG Z P, et al. Remaining useful life prediction for lithium-ion batteries based on a hybrid model combining the long short-term memory and Elman neural networks[J].Journal of Energy Storage,2019,21:510-518.

[19]SEVERSON K A,ATTIA P M, JIN N, et al. Data-driven prediction of battery cycle life before capacity degradation[J]. Nature Energy,2019,4(5):383-391.

[20]LI Y, ABDEL-MONEM M, GOPALAKRISHNAN R, et al. A quick on-line state of health estimation method for Li-ion battery with incremental capacity curves processed by Gaussian filter[J].Journal of Power Sources,2018,373:40-53.

[21]LI X Y, WANG Z P, ZHANG L, et al. State-of-health estimation for Li-ion batteries by combing the incremental capacity analysis method with grey relational analysis[J]. Journal of Power Sources,2019,410/411:106-114.

[22]WANG P, MENG P, SONG B W. Response surface method using grey relational analysis for decision making in weapon system selection[J]. Journal of Systems Engineering and Electronics,2014,25(2):265-272.

[23]LU C, TAO L F, FAN H Z. Li-ion battery capacity estimation: A geometrical approach[J]. Journal of Power Sources, 2014, 261:141-147.

[24]SUN W Z, WANG J S. Elman neural network soft-sensor model of conversion velocity in polymerization process optimized by chaos whale optimization algorithm[J].IEEE Access,2017,5:13062-13076.

[25]LIU H, TIAN H Q, LIANG X F, et al. Wind speed forecasting approach using secondary decomposition algorithm and Elman neural networks[J].Applied Energy,2015,157:183-194.

[26]HE W,WILLIARD N,OSTERMAN M,et al.Prognostics of lithiumion batteries based on dempster-shafer theory and the bayesian monte carlo method[J]. Journal of Power Sources, 2011, 196(23):10314-10321.