基于CAE技术的谷物集装箱安全性分析

摘  要：文章推导出颗粒介质对集装箱壁面载荷的计算公式，采用CAE静力学仿真技术，建立谷物集装箱两种使用工况下的有限元模型，利用CAE软件模拟谷物集装箱刚度和强度，根据标准集装箱设计原则，分析标准干货集装箱用于存储谷物的可行性，并探讨谷物集装箱优化设计方向，这对其他用于存储颗粒介质的产品的设计具有一定参考作用。

关键词：集装箱;颗粒介质;CAE;优化设计

中图分类号：TP391.9           文献标识码：A文章编号：2096-4706（2022）04-0115-03

Safety Analysis of Grain Container Based on CAE Technology

SHEN Sainan

（World Oriental International Container （Qidong） Co.， Ltd.， Qidong  226265， China）

Abstract： In this paper， the calculation formula of the load of granular medium on the container wall is derived， and the finite element model of grain container under two use conditions is established by using CAE static simulation technology， simulates the stiffness and strength of the grain container by using the CAE software， analyzes the feasibility of the standard dry cargo container for storing grain according to the design principle of the standard container， and discusses the optimization design direction of the grain container， this has a certain reference for the design of other products for storing granular medium.

Keywords： container; granular medium; CAE; optimization design

0  引  言

集裝箱作为陆运和海运的重要载货媒介，是多式联运的重要一环，而探索标准集装箱产品的特殊用途，一直是业界热点和难点，比如考虑经济性，要求标准集装箱既可以作为普通干箱发挥运输用途，又可以储存谷物等颗粒介质发挥仓储功能。本文针对20尺标准干货集装箱的结构进行简单更改，探索其用于存储谷物的安全性和优化设计方向，这对用于存储颗粒介质的其他产品的壁面载荷计算、设计、安全性分析和优化具有一定参考作用。

1  颗粒介质对集装箱壁面载荷的计算

普通固体货物放置于集装箱中，集装箱壁面所受最大载荷可以参考各船级社和其他机构关于集装箱强度设计的检验标准[1]。而液体放置于集装箱中时，集装箱壁面所受载荷可以通过简单公式计算获得。颗粒介质区别于普通固体货物与液体，集装箱填装颗粒物时，箱体形成事实上的筒仓结构。筒仓底部所受载重在受力截面上均布，筒仓立面和斜面所受物料压强参考《GB 50077-2017 钢筋混凝土筒仓设计标准》（以下简称“筒仓标准”），分深仓与浅仓两种情况求解[2]。根据集装箱装载谷物时放置方式的不同，分为垂直放置（深仓）与水平放置（浅仓）两种使用工况。

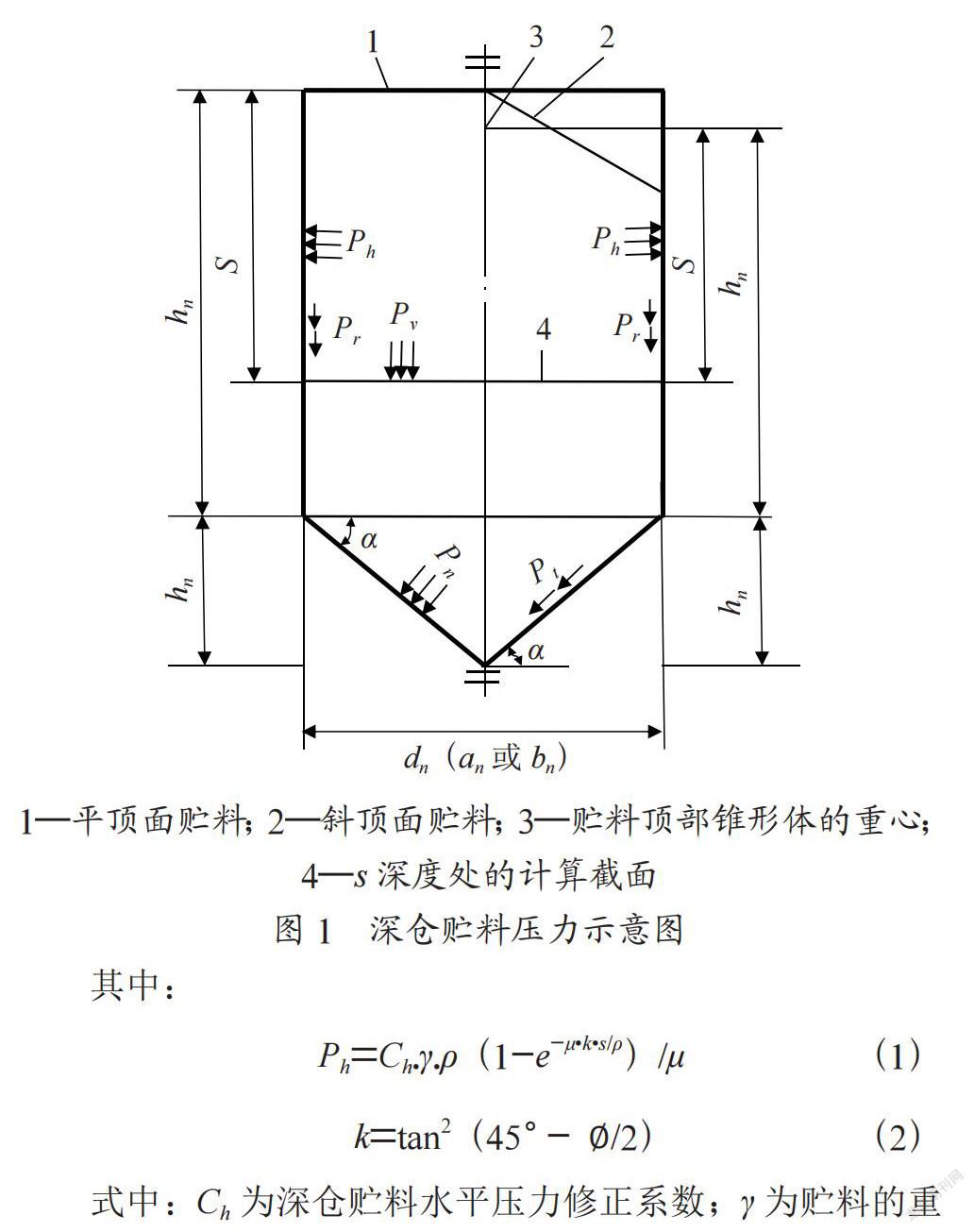
1.1  深仓壁面载荷计算

如图1所示，对于深仓，贮料顶面、贮料顶部锥形体重心以下，距离S（m）处的水平截面上，仓壁所受水平压强Ph（kPa）应按下列公式计算：

其中：

Ph=Ch·γ·ρ（1-e-μ·k·s/ρ）/μ   （1）

k=tan2（45°- ∅/2）（2）

式中：Ch为深仓贮料水平压力修正系数;γ为贮料的重力密度（KN/m3）;ρ为筒仓水平净截面的水力半径（m）;e为自然对数的底;s为贮料顶面或贮料椎体重心至计算截面的距离（m）;μ为料对仓壁的摩擦系数;k为侧压力系数;∅为贮料的内摩擦角（°）;仓底或漏斗顶面处所受竖向压强Pv（KPa）应按下式计算：

（3）

式中：Cv为深仓贮料竖向压力修正系数;hn为贮料计算高度（m）。

注：当按上式计算的Pv值大于γhn值，γhn应为浅仓的竖向压力。

贮料重力密度γ参见筒仓标准附录A《贮料的物理特性参数》，Ch值参见筒仓标准表4.2.5-1，Cv值参见筒仓标准表4.2.5-2。

针对集装箱，hn（m）=贮料顶面-贮料底面。

筒仓仓壁水平任意净截面，矩形筒仓任意净截面的水力半径（ρ（m）应按下列公式计算：

ρ=A/U（4）

ρ=anbn/2（an+bn）（5）

式中，A为筒仓水平截面的净面积（m2）;U为净截面的周长（m）;an为矩形筒仓仓壁长边内边缘的边长;bn为矩形筒仓仓壁短边内边缘的边长。

1.2  浅仓壁面载荷计算

如图2所示，平面为圆形，矩形的浅仓，贮料压力的计算应符合以下规定：

1—平顶面贮料;2—斜顶面贮料;3—贮料顶部锥形体的重心;4—s深度处的计算截面

图2  浅仓贮料压力示意图

贮料顶面、贮料顶部锥形体重心以下，距离s（m）处的水平截面上，作用于仓壁上的水平压强Ph（KPa）应按下式计算：

Ph=kγs  （6）

筒仓的贮料计算高度hn与其内径dn的比大于1.0且小于1.5、矩形平面的短边的bn的比大于0.4且小于1.5时，除按式（6）计算外，还应按式（1）计算贮料压力，取其二者计算结果的最大值。

贮料顶面、贮料锥形顶重心以下距离s（m）处竖向压强Pv（KPa）应按下式计算：

Pv=γs （7）

2  有限元分析模型的建立

谷物箱设计方案为：将20尺标准干箱侧壁厚度从2 mm改为3 mm后门端朝上垂直放置于地面，打开门端，装载28吨谷物后，关闭门端再翻转90°水平静置于地面。根据集装箱产品设计总原则，两种工况下谷物箱主结构不允许大面积屈服，箱体永久变形不可导致尺寸超差，且门端仍能开合。

由于采用真实物理试验评估谷物箱安全性存在诸多限制与缺陷，比如时间周期长、经济费用高和安全隐患多，因此本文采用CAE静力学仿真技术评估箱体刚度和强度性能，判定方案可行性。

模型方面，为了提高计算效率同时保证计算结果准确性，本文对物理模型做合理简化。第一、删除与主结构无关的零件，如绳钩、胶条和铭牌等;第二、简化仅用于传力而不作为主要分析对象的零件，如门铰链、锁头和锁座等;第三、去除小于5 mm的倒圆和倒角以提高网格质量降低网格数量;第四、考虑谷物集装箱左右对称，计算时采用1/2对称模型，降低计算规模，节省计算时间;第五、垂直放置工况，门页承开启状态，对结构无刚度补充作用，因此计算该工况时删去门页[3]。

材料方面，20尺标准干箱主结构材质为SPA-H，弹性模量2.1E5 MPa，泊松比0.3，屈服强度355 MPa[4]。

载荷方面，箱体装载28吨粮食，根据上文公式推导，垂直放置工况载荷参数如表1所示。

水平放置工况载荷参数如表2所示。

表1代入函数式（1）（3）可得深仓壁水平压强Ph1和竖直压强Pv2，表2代入函数式（6）（7）可得浅仓仓壁水平压强Ph2和竖直压强Pv2。

位移边界条件方面，垂直放置时，前角件端面固定约束，水平放置时，底角件端面固定约束。

求解算法方面，采用几何非线性算法，计算时更新每个载荷步的刚度矩阵，以准确跟踪主结构的大跨度受压区域在加载过程中的刚度变化情况[5]。

3  可行性分析结果

垂直放置工况，箱体性能如图3所示。

垂直放置工况，侧板与底架基本处于弹性变形状态，但顶板与前墙板大片屈服（铁灰色区域）且变形过大，结构在装载和存储谷物时存在安全隐患。

水平放置工况，箱体性能如图4所示。

水平放置工况，顶板、前墙板、侧板、门页和底架基本处于弹性变形状态，可认为结构安全。

由于结构设计需同时满足两种使用工况，因此判定标准集装箱用于装载和储存谷物设计方案不可行，并严禁标准集装箱垂直放置装载谷物。

4  优化设计

谷物箱使用过程中的安全隐患主要集中在垂直放置工况下的顶板和前墙板。考虑经济性、工艺复杂性和制作时间等因素，本文提出两种加强方案，方案一侧板波深从36 mm改为40 mm，每侧增加2根60×60×3.0 mm立柱;方案二每侧增加1根60×60×3.0 mm纵向加强管，顶部增加2根60×60×3.0 mm纵向加强管，计算结果如表3、表4所示。

计算结果显示，对侧板和顶板进行加强后，侧板和顶板的性能均得到了有效提升，但由于三种方案的侧壁、顶板与前墙板变形过大且大片屈服，均无法满足标准干箱用于垂直放置装载和储存粮食的需求。基于本文分析结果，笔者不建议将标准集装箱直接或简单更改后用于谷物的装载和存储。

后续探索集装箱产品用于储存谷物或其他颗粒介质时，可以从以下两个方面进行：第一、通过加厚侧壁和前墙板、加大波深或在凹波内放置立柱的方式，优化侧壁和前墙板性能，达到给结构补充刚度的作用;第二、将谷物箱设计为硬开顶结构，使谷物可以从顶部装卸，避免集装箱垂直放置装粮工况，最终保证集装箱装载谷物的安全性。

5  结  论

目前情况下，不建议将标准集装箱用于装载和存储谷物，后续可以尝试通过优化设计，同时满足集装箱的基本运输功能与装载存储谷物功能。

参考文献：

[1] 中国船级社.集装箱验箱规范 [M].北京：人民交通出版社，2016.

[2] 中华人民共和国住房和城乡建设部.钢筋混凝土筒仓设计标准：GB50077-2017  [S].北京：中国计划出版社，2018.

[3] 欧贺国，方献军，洪清泉.RADIOSS理论基础与工程应用 [M].北京：机械工业出版社，2013.

[4] 刘鸿文.材料力学 [M].北京：高等教育出版社，1992.

[5] 李黎明.ANSYS有限元分析實用教程 [M].北京：清华大学出版社，2005.

作者简介：沈赛男（1988—），女，汉族，江苏南通人，CAE工程师，硕士，主要研究方向：工程结构分析与优化设计研究。