基于误差修正NLSTM 神经网络的无人机航迹预测

梁天宇, 高 永, 刘军民, 惠永昌

(1. 西安交通大学数学与统计学院，西安 710049; 2. 海军航空大学航空基础学院，烟台 264001)

0 引言

无人机全称“无人驾驶飞行器”，英文缩写为“UAV”(Unmanned Aerial Vehicle)，是利用无线电遥控设备和自备的程序控制装置操纵的不载人飞机[1]。它被广泛应用于军用和民用等领域。随着无人机产业的蓬勃发展，无人机航迹预测也成为当前世界研究的热点。例如，对无人机进行快速准确的航迹预测可以提高作战效率，进行任务规划和及时提供冲突解决方案；通过航迹预测可以建立有效的无人机监管系统，保障民航航班的运行安全等。

目前，国内外对于飞行器航迹预测的方法主要包括两类：空气动力学方法和无参数估计方法。空气动力学模型在航迹预测的应用中普遍存在参数过多、预测精度较低等问题[2]。无参数估计方法因不考虑飞行器动力学参数从而简化模型，被广泛研究并应用于航迹预测。

无参数估计方法可分为传统的统计学算法和当前发展迅猛的神经网络算法。统计学方法主要是利用数理统计的方法处理历史数据，对历史数据进行曲线拟合以及参数估计，不断提高预测精度，包括回归预测法、蒙特卡罗法、卡尔曼滤波算法等。例如，Wu 和Pan[3]提出一种基于数据挖掘的飞行轨迹预测模型，采用二元线性回归法预测下一次的飞行时间，从大量历史位置数据分析飞机每个时间点的位置；Lymperopoulos 和Lygeros[4]证明了序列蒙特卡罗法在多飞行器航迹预测中的有效性；Prevost 等[5]采用改进的卡尔曼滤波(Improved Kalman Filter, IKF)算法估计无人机追踪的运动目标的状态，并通过计算预测误差来评价预测轨迹的质量；罗兆文等[6]建立了基于滑窗多项式最小二乘拟合的航迹预测法，对于短期预测有较好的效果。

在基于神经网络的航迹预测方面，徐婷婷等[7]设计了三层反向传播(Back Propagation, BP)神经网络模型用于船舶的航迹实时预测，其结果体现了神经网络较强的非线性逼近能力与鲁棒性。杨彬和贺正洪[8]利用广义回归神经网络(Generalized Regression Neural Network, GRNN)对高超声速飞行器进行轨迹预测。吴一凡和冉晓旻[9]将卷积神经网络(Convolutional Neural Networks, CNN)引入到航迹预测中，并且证明了其在小样本航迹预测中具有较高的准确性。

以上应用于航迹预测的算法各有优点，但是仅把航迹数据看出空间中的独立数据点，没有充分利用其轨迹时序上的相关性。循环神经网络(Recurrent Neural Networks,RNN)是一种具有代表性的神经网络模型，其结构非常适用于处理时间、空间上有强关联的动态序列数据。然而，传统的RNN 由于其结构过于简单，对序列数据的记忆能力会逐渐下降，不能存储长期记忆，即无法解决长期依赖问题。为克服这一问题，Hochreiter 和Schmidhuber[10]提出了长短期记忆神经网络(Long Short-Term Memory, LSTM)。它改进了原RNN 中的记忆单元，以不同的方式计算隐层神经元的状态，从而使得神经网络具有更长时间的记忆能力。目前，LSTM 已被广泛应用于各个领域的预测研究中。

鉴于此，本文首次提出利用RNN 以及其变体LSTM 对无人机飞行轨迹进行预测，传统的LSTM 用于预测时仍存在精度不够高等问题。针对传统LSTM 模型的不足，本文提出一种带误差修正的嵌套长短期记忆网络(Error-corrected Nested LSTMs, ENLSTM)航迹预测模型。该模型能够通过对历史数据的训练实现对无人机的航迹预测，并且利用误差模型对网络进行修正，得到更准确的预测航迹。在无人机的模拟飞行数据和真实行训练数据上的仿真对比实验表明所提出的ENLSTM 模型能更加有效地预测无人机的飞行轨迹，证实模型的可行性。

1 相关理论

1.1 RNN 循环神经网络

循环神经网络(RNN)是一类专门用于处理序列数据的神经网络，比如时间序列、文本语句、语音等。RNN 不仅考虑前一个时刻输入的影响，并且考虑以前时刻输入的影响，所以赋予了网络“记忆”的功能。RNN 的向前传播中折叠了一个循环计算的重复结构，即对于一个序列，其当前状态ht包含了过去所有状态ht−1对其的影响，以及当前时刻外部输入xt的影响，即

一个最简单的RNN 架构如图1 所示，左边是循环未展开的部分，右边是展开的结构。RNN 主要由输入层、隐藏层和输出层组成，隐藏层的箭头表示数据的循环更新，即实现网络的记忆功能。其中x表示输入的样本，o表示输出的预测，W表示隐藏层从前一时刻转移到后一时刻的权重矩阵，U表示输入层到隐藏层的权重矩阵，V表示隐藏层到输出层的权重矩阵，网络中每个单元共享一组(W,U,V)，实现参数共享可极大地降低计算量。

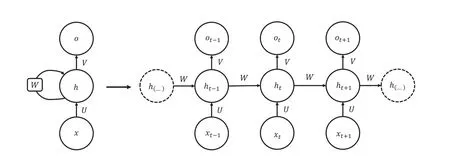
图1 RNN 网络结构图

根据图1 的网络结构，RNN 的前向传播过程如下：

1) 时刻t的隐状态

2) 时刻t预测输出

其中f、g均为激活函数，用于筛选重要信息。f可以采用tanh、relu 和sigmoid 函数等，g通常取为softmax 函数；

3) 对于离散分类任务，该网络的损失函数一般为交叉熵，而对于连续预测任务，损失函数通常是均方误差，即

通过将每个时刻的输出值的误差反向传播和梯度下降法，可以对RNN 的权重参数进行更新，在不断调整参数的过程中提高模型性能。

1.2 NLSTM 嵌套长短期记忆网络

随着时间序列变长，RNN 的反向传播过程中可能会出现梯度消失和梯度爆炸的问题，这导致其难以传递相隔较远的信息。因此，RNN 的一系列变种算法被提出，其中最具有代表性的是LSTM。如果说RNN 能够使得网络拥有短暂的“记忆”，那么LSTM 则是扩展了网络的“记忆”，能够解决长期依赖问题。LSTM 在RNN 的基础上加了三个门来控制，网络结构为图2。

如图2 所示，LSTM 神经网络也如同RNN 分为输入层、隐藏层和输出层，隐藏层中增加了三个门结构，分别是遗忘门、输入门和输出门。

图2 LSTM 网络结构图

1) 遗忘门决定保留多少上一层的细胞ct−1中的旧记忆信息，流入当前时刻的xt与上一时刻传递过来的状态ht−1，通过对应的所有事件步共享的权重Wxf、Whf，偏移bf进行线性组合，并通过sigmoid 函数进行处理后得到对旧记忆信息的保留比例ft，即

2) 输入门控制了有多少新记忆信息可以流入，即生成新记忆信息和新记忆信息的使用比例it，接着融合旧信息与新信息生成新的记忆细胞ct，对应下式

其中⊙表示矩阵的元素相乘，tanh 为激活函数。

3) 基于新的记忆细胞ct以及输出门计算的比例值ot，得到最终的输出ht

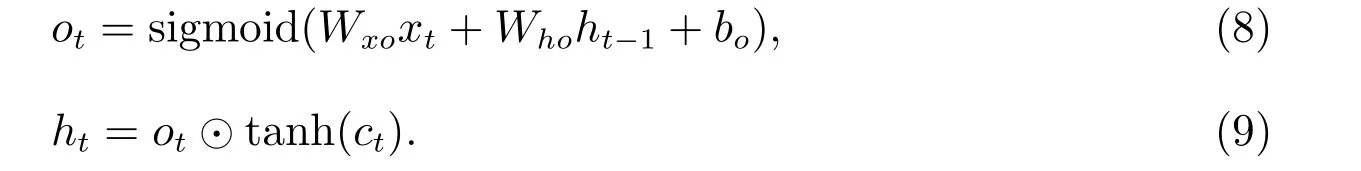
关于LSTM 模型的变体有很多，为了提高模型的精度，增加LSTM 网络的深度是一种较为常用的方法。嵌套长短期记忆网络(Nested LSTMs, NLSTM)[11]，则是通过加入一个状态函数，从而有选择性地访问内部记忆信息，使得网络能够处理更长时间规模的序列，网络结构如图3 所示。其中状态函数mt用于替换LSTM 网络中ct计算式(7)中的加和，即在NLSTM 中

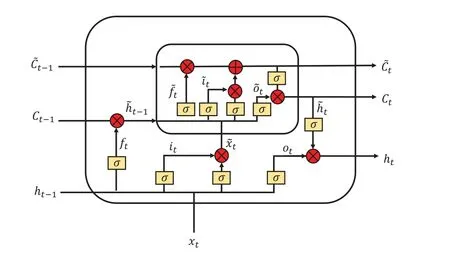
图3 Nested LSTMs 网络结构图

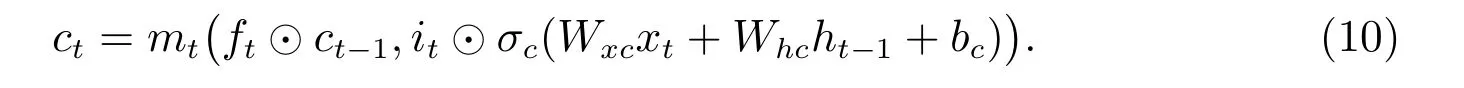
如果将mt作为一个LSTM 记忆单元，则NLSTM 中记忆函数的输入和隐藏状态为

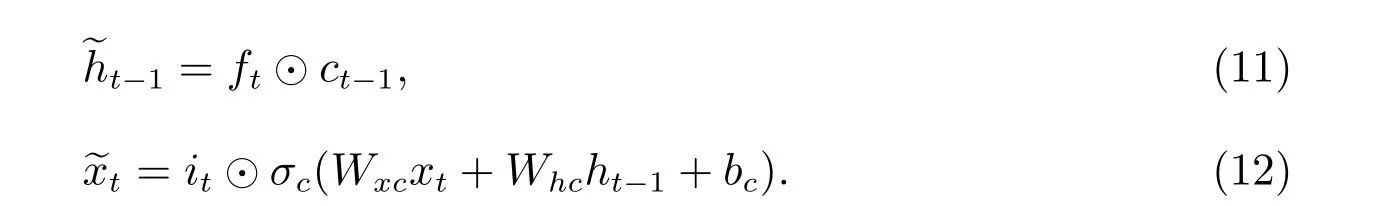
那么NLSTM 的内部计算过程如下

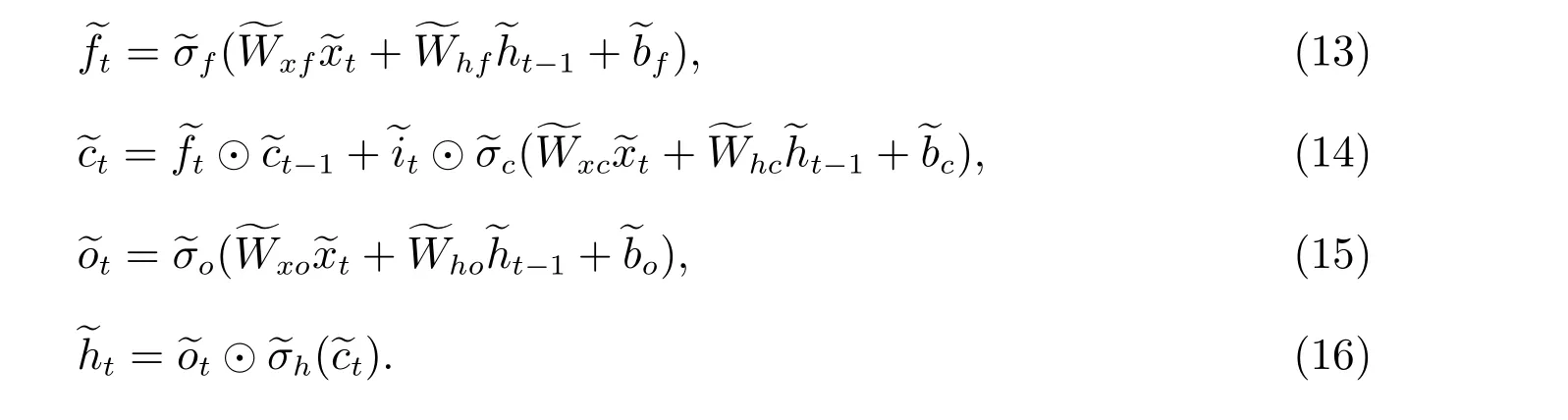
NLSTM 的外部记忆信息为

通过嵌套长短期记忆网络的架构可以看出，它创造了一种记忆的时间层级，通过门控的方式去访问内部记忆，以便于选择性地去访问长期记忆信息。同时增加了网络的深度，有效提高模型的性能。

2 带误差修正的NLSTM 网络预测无人机航迹模型

2.1 误差修正

影响无人机飞行轨迹预测产生误差的因素有很多，首先良好的预测模型需要高精度的数据作为支撑，而由于数据采集与监控系统采集的数据可能存在误差以及采样频率不稳定等原因造成产生异常数据是影响预测精度的重要原因[12]。其次，模型自身存在局限性。进行轨迹预测需要建立数学模型，即将实际问题进行抽象、化简，模型只能在理论上以一定的精度逼近实际问题而无法真实地刻画[13]。例如由于网络训练精度限制以及参数设置，误差不可避免地存在。最后，预测时长和样本容量大小的选取也会对预测精度产生影响。例如，随着预测序列长度的增加以及新的预测数据的影响，误差会逐步累积。

为了进一步缩小预测误差以提高预测结果的可信度，需要进行误差修正。早期的误差修正技术出现在对测量仪器的校正上，随着计算机的飞速发展，误差修正在技术实现上有了飞跃的进步，程序化、自动化和环境自适应修正得以实现。信号处理技术的发展更是充实和完善了误差修正的建模技术。在误差建模方面，其基本算法包括解算方法、仿真方法和一些辅助方法等，近年来还出现了一些计算机集成算法工具，如Matlab 工具箱，为误差建模的实施提供很大的帮助[14]。

本文为了提高预测精度，提出误差修正策略。在建立NLSTM 预测模型后，利用误差建模技术对预测轨迹进行校正，建立误差模型

2.2 算法模型

本文基于深度学习框架Tensorflow 建立NLSTM 网络，各部分结构与参数设置如下：

1) 隐藏层结构与参数：考虑到输入样本的数量较少，本文将隐藏层层数设为1，即建立一个单层的NLSTM 网络，神经元个数为20，添加无激活函数的全连接层，嵌套深度设置为2；

2) 模型训练参数：模型在训练前需要指定损失函数和优化器。本文选择均方误差作为损失函数和Adagrad 优化器不断更新参数，进行预测模型的优化。设置训练批尺寸为50，训练轮数为1 000；

3) 预测评价指标：为了便于预测值与真实值比较，分析模型的预测效果，选择均方根误差作为评价指标

结合2.1 的误差修正，本文提出的ENLSTM 预测模型整体框架为图4。

图4 ENLSTM 预测模型框架

3 实验及结果分析

为了验证本文提出的ENLSTM 网络模型对无人机航迹预测的可行性和普适性，实验部分对模拟飞行数据和无人机实际飞行数据分别进行预测，根据轨迹预测图及预测误差进行分析。

3.1 数据描述

1) 模拟飞行数据采用四种含有随机噪声的三维曲线，使用70%的数据点作为网络的训练集，剩下30%作为测试集。参数方程式及取值范围如表1 所示。

表1 模拟数据的参数方程式及取值范围

2) 实验使用的无人机训练飞行的真实数据是通过Mission Planner 加载航线日志，导出mat 格式的飞行数据再利用Matlab 软件加载数据。接着从GPS 标签中选择经度、纬度和高度三个航迹指标作为网络的输入进行无人机的航迹预测。由于该无人机的四边航线飞行训练过程中，分为上升、平飞和下滑三个阶段，其中平飞阶段为27 圈，采样点数量为9 477，本实验使用平飞阶段前26 圈的经度、纬度和高度三个航迹指标数据作为模型的训练集，剩下的数据用于测试。

3.2 数据预处理

数据的预处理包括数据归一化和构造时间序列样本集两部分。

1) 数据归一化

由于输入变量的量纲不同，为了消除其影响，本文选择对输入的样本数据，即经纬度和高度进行z-score 标准化处理，以提高预测的准确性，公式如下

2) 构造时间序列样本集

设定时间步长为T，用前T个样本点的历史数据预测下一时刻的数值，即采用时刻t −T到时刻t −1 的数据作为预测的输入序列，时刻t的数据作为预测的输出，以此生成连贯的时间序列类型样本集。

3.3 模型参数分析

为了得到误差相对较小的最优模型，首先进行ENLSTM 预测模型部分超参数的分析与优化。根据经验以及样本长度，分别选择20、30、40、50 作为预测的时间步长和0.12、0.1、0.08 作为Adagrad 优化器的学习率训练模型，并且计算测试数据的预测值与真实值的均方根误差RMSE。表2 为使用ENLSTM 模型对无人机真实飞行轨迹进行预测的误差。

表2 不同时间步长和学习率下预测模型的RMSE

根据表2，选出均方根误差最小的模型参数，即预测时间步长设为50，优化器的学习率为0.1，此时RMSE 为0.109 2。

3.4 对比试验

为了验证ENLSTM 模型预测效果的优越性，本文使用BP 神经网络、单层RNN 和单层LSTM 分别对模拟数据和对实际飞行数据进行预测，对比效果。对于BP 神经网络，本文设计一个三层的BP 神经网络，输入长度为50 个时刻的位置坐标，隐藏层的节点数为20 个，输出为下一时刻的位置坐标。设置隐藏层的传递函数为对数S 型函数，输出层的传递函数则为线性函数；训练方法采用Levenberg-Marquardt 算法；学习率设为0.1；训练次数设为1 000。单层RNN 和单层LSTM 模型的参数设置和ENLSTM 类似。

四个模型对于模拟飞行数据的预测曲线为图5 至图8，对于真实飞行数据的预测曲线为图9，其中黑色实线为真实航迹，蓝色星号线为ENLSTM 的预测轨迹，虚线为LSTM、RNN 和BP 三种模型的预测结果。可以较为直观地看出，ENLSTM 模型的预测轨迹更接近于真实轨迹。

图5 模拟数据1 的预测曲线与真实曲线

图6 模拟数据2 的预测曲线与真实曲线

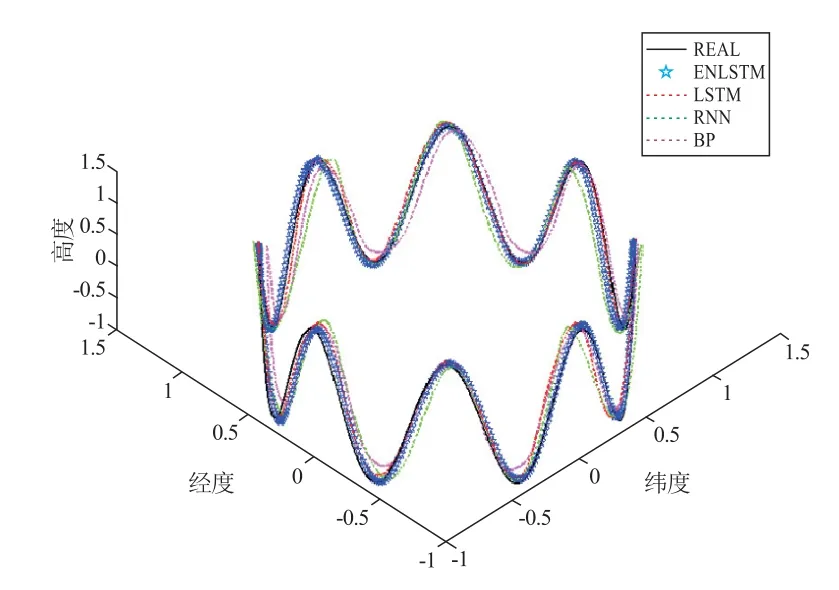
图7 模拟数据3 的预测曲线与真实曲线

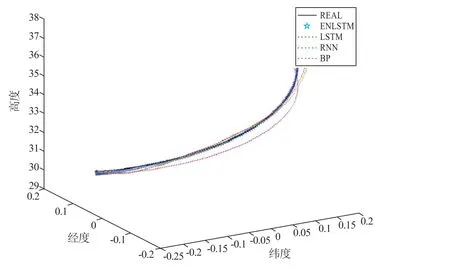
图8 模拟数据4 的预测曲线与真实曲线

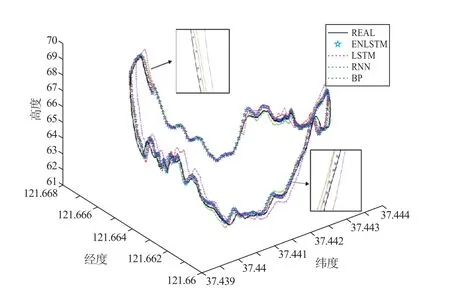
图9 真实数据的预测轨迹与真实轨迹

通过计算，四种模型预测结果的RMSE 为表3。针对模拟数据，ENLSTM 模型的预测序列与真实序列的误差RMSE 分别为0.086 1、0.021 1、0.025 5 和0.087 1，实际飞行数据的预测误差RMSE 为0.109 2，比起LSTM、RNN 和BP 模型的预测结果，误差都有了显著减小，说明本文提出的模型在预测性能方面有了明显的改进。并且从四种模型的预测误差依次递减，可以说明循环神经网络相对BP 神经网络在时间序列数据的预测上更具有优势，以及基于基础循环神经网络的逐步改进提升了模型的预测能力。

表3 四种模型预测结果的RMSE

4 总结与展望

本文将NLSTM 神经网络应用到无人机的航迹预测中，并且通过误差建模对预测值进行修正。将提出的ENLSTM 预测模型分别应用到无人机的模拟飞行轨迹和真实飞行轨迹，通过不断优化参数，可以使模型达到较好的预测效果。同时与BP、RNN、LSTM 神经网络对比，实验表明在参数基本相同的情况下，ENLSTM 模型预测精度更高。针对无人机的航迹预测问题，ENLSTM 模型有着较好的应用效果。同时ENLSTM 仍存在权重参数较多使得训练时间较长的问题，下一步将对ENLSTM 模型的网络结构进行优化，使得预测结果准确且高效。