深层页岩气水平井钻进中井筒-地层瞬态传热模型

2022-07-06吴鹏程钟成旭严俊涛万秀梅陈烨杨谋

石油钻采工艺 2022年1期

吴鹏程钟成旭严俊涛万秀梅陈烨杨谋

1. 中国石油西南油气田公司页岩气研究院；2. 中国石油川渝页岩气前线指挥部；3. 油气藏地质及开发工程国家重点实验室·西南石油大学

0 引言

四川深层页岩气资源丰富，埋深在3800～4300 m左右，井底温度高，水平井钻进过程中井底循环温度均超过140 ℃。如泸202井在井深5248 m、垂深4288 m处井筒温度为140 ℃；在井深5400 m、垂深4312 m处井筒温度为145 ℃。当循环温度超过135 ℃时，频繁发生入井仪器电子元器件损坏、定子橡胶开裂等故障，导致频繁起下钻更换工具和仪器，影响钻井周期。为此，分析了钻井参数、水平段长度、流体性能、入口温度对井筒温度的影响，开展了深层页岩气水平井井底循环温度影响因素研究，以确保有效安全钻进。

井筒温度影响因素包括钻井参数(钻井液排量、钻进时间)、流体性能(钻井液密度和比热容、入口温度)、井身结构(裸眼段长度、套管层次、井眼尺寸)等［1］。钻井过程中，井筒-地层为耦合体，井筒-地层各控制区域(钻柱内、钻柱壁、环空、井壁、近井壁套管、水泥环及岩石)之间的热量相互影响，每个控制区域热量守恒模型均涉及一个偏微分方程。为此，若要知晓井筒温度分布情况，涉及井筒-地层十余个偏微分方程联立求解，求解难度大。Raymond率先建立了井筒-地层瞬态传热数值模型［2］，但在模型求解上忽略了套管传热影响，将环空与钻柱内热交换应用综合传热系数来表述，使得计算温度低于实际工况［3］。在Raymond模型基础上，国内外学者采用有限差分和有限元方法对瞬态传热模型进行求解，获得了考虑不同环境、不同工况下的井筒瞬态温度分布特征，Marshall等分析了正常钻进过程中井筒温度敏感性因素［4-8］；Garcia等研究了漏失、溢流对井筒温度分布的影响［9-10］；宋洵成等研究了深水隔水管对井筒温度分布的影响［11］；刘洋等考察了尾管注水泥及水泥浆候凝期间井筒温度分布特征［12-14］。

上述传热模型主要应用于评价直井热交换现象，深层页岩气水平井钻进中热交换与直井的区别为：(1)井筒温度初始条件和边界条件不同。直井初始温度仅与井深相关，页岩气水平井初始地温为井深和井斜角的函数(假设同一平面上地温相等)。(2)循环温度差异。流体循环是将环空下部井段温度携带至上部井段，使得下部温度低于原始地温，上部井段高于原始地温，然而水平井钻进过程中，靶点A至靶点B环空流体的初始温度均为原始地温，在循环初期，流经靶点B流体温度为原始地温加上流体循环摩阻生热附加的温度，使得水平井初始钻进时下部井段温度要高于原始地温，若此时用原始地温来设计流体性能、优选井下动力钻具的服役环境则难以满足实际要求。(3)循环排量对温度影响差异。直井增加排量，能将下部井段流体携带至上部井段，降低下部井段温度；而水平井增加排量，由于水平段流体温度为原始地温，增加排量摩阻生热量更多，使得环空温度更高，因此，排量过大不利于降温。尽管文献[7]也开展了页岩气水平井井筒温度场模拟，但水平井与直井间的传热机理差异尚未深入研究与报道，制约了深层页岩气钻井过程中井筒降温技术的应用与推广。

笔者基于能量守恒原理，考虑流体循环摩阻生热对井筒温度的影响，建立了深层页岩气井实际井身结构与钻柱组合条件下井筒-地层各控制区域的瞬态传热模型，并采用快速收敛的全隐式有限差分法对数学模型求解，获得井筒-地层瞬态温度分布特征。同时，开展了钻井参数、流体性能对环空温度分布的敏感因素分析，研究各参数对井筒温度影响规律。在此基础上，结合旋转导向工具服役环境温度，开展了在有、无地面降温装置条件下深层页岩气水平段延伸距离分析，并应用现场数据验证了数学模型的有效性。本论文研究成果为深层页岩气井钻前温度预测、钻进优化、钻后评价提供了可靠的理论基础。

1 物理模型与假设条件

1.1 物理模型

在深层页岩气井钻进过程中，井筒-地层各区域发生着复杂的热交换，使得钻柱内和环空流体温度随钻进时间的变化而改变。钻井液在地面以一定温度(Tin)从钻柱内向下流动，对于钻柱内流动传热控制单元，热量变化包括：(1)流体向下流入的热量Qp(z)与流出热量Qp(z+dz)之差；(2)从钻柱内壁以热对流方式传入管内的热量Qpa；(3)流体循环摩阻产生的热量Qpf。流体向下流经钻头喷嘴后流入环空，在井底钻柱内流体温度与环空流体温度相等。在环空向上流动过程中，控制单元热量变化包括：(1)向上流动流入的热量Qa(z+dz)与流出热量Qa(z)之差；(2)在钻柱外壁以热对流方式传入钻柱壁的热量Qap；(3)在井壁以热对流方式传入环空的热量QFa；(4)流体循环摩阻产生的热量Qaf。流体经一个循环周期从环空返至地面，该流动传热过程如图1所示。

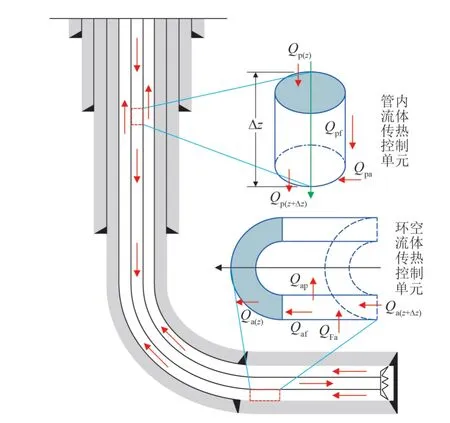
图1 页岩气水平井井筒传热示意图Fig. 1 Schematic diagram of heat transfer in shale gas horizontal well

1.2 假设条件

根据地层、水泥环、套管和井筒的热传递机理，采用能量平衡相关理论建立井筒与地层之间的传热方程，对所建立的模型进行如下基本假设：(1)在地层、水泥环空和套管仅有径向和轴向上的热传导，忽略岩石孔隙中流体产生的热对流作用；(2)井筒中钻井液为单相不可压缩流体，且在井筒环空、套管环空及地层中液体无相态变化；(3)相同岩性岩石热力学参数具有各向同性，即热导率和比热容在地层中某一位置的垂直方向和水平方向相等，但岩石的密度、比热容和热导率随埋藏深度而变化；(4)忽略钻柱内和环空钻井液轴向导热和径向上的温度梯度［15］；(5)距井壁一定距离的地层温度不受井筒内传热过程的影响。

2 数学模型

在钻进过程中，井筒-地层各控制区域热量为耦合体，包括钻柱内、钻柱壁、环空、井壁及近井壁地层。各控制区域热量互相扰动，使得井筒-地层热量随钻进时间而变化，因此，若需要知道钻进过程中环空温度演变特性，则需要建立井筒-地层各控制区域瞬态传热数学模型。

2.1 钻柱内流体传热模型

结合传热物理模型中表述的传热机理，则钻柱内传热模型建立如下。

钻柱内流体向下流动过程中流入微分单元的热量

钻柱内钻井液与钻柱内壁在径向上热对流交换的热量

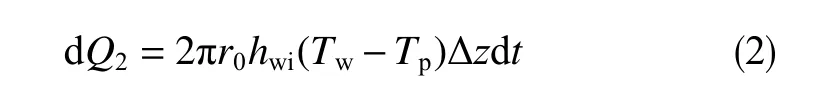
钻柱内流体循环摩阻产生的热量

单位时间内，钻柱内微分单元内能的变化量

基于能量守恒，将式(1)～(4)整理可得

等式两边同时除以∆zdt，则有

将式(6)整理可得钻柱内循环温度模型

式中， ρm为钻井液密度，kg/m3；cm为钻井液比热容，J/(kg· ℃ )；Tp为钻柱内钻井液温度，℃；Tw为钻柱壁温度，℃；hwi为钻柱内壁面对流换热系数，W/(m2· ℃ )；Q为钻井液排量，m3/s；Qp为钻柱内流体热源项，W/m；为钻柱内径，m。

2.2 钻柱壁传热模型

影响钻柱壁热量的因素为：钻柱壁在轴向上的热传导、钻柱外壁与环空流体的热对流、钻柱内壁与环空流体的热对流、钻柱壁热量在单位时间的变化。则由能量守恒原理，该模型可以表述为

式中， ρw为钻柱密度，kg/m3；cw为钻井液比热容，J/(kg· ℃ )；Ta为环空钻井液温度，℃；hwo为钻柱外壁面对流换热系数，W/(m2· ℃ )； λw为钻柱热导率，W/(m· ℃ )；r1为钻柱外径，m。

2.3 环空流体传热模型

环空流体热量影响因素包括：钻井液向上流动携带的热量、钻柱外壁与流体发生的热对流、井壁与环空流体发生的热对流、环空流体循环摩阻产生的热量、环空钻井液内能的变化。基于能量守恒，则环空流体传热数学模型为

式中，hb为井眼对流换热系数，W/(m2· ℃ )；r2为井眼半径，m；Tc1为井壁温度，℃；Qa为环空内流体热源项，W/m。

2.4 井壁传热模型

井壁由套管和岩石构成，则井壁热量影响因素为：轴向上发生的热传导、井壁内侧环空流体与井壁发生的热对流、井壁外处临近的水泥石(或滞留钻井液)/岩石与套管产生的热传导、微元段自身能量的变化。基于能量守恒原理，井壁传热模型为

式中，λc1为套管/岩石热导率，W/(m· ℃ )；λs1为水泥环/岩石热导率，W/(m· ℃ )；Ts1为水泥环/岩石温度，℃；ρc1为套管/岩石密度，kg/m3；cc1为套管/岩石比热容，J/(kg· ℃ )；r3为套管外径，m。

2.5 近井壁地层传热模型

近井壁地层有多层套管、水泥环及地层构成，其传热模型可看成多个圆筒壁在径向和轴向上的热传导，数学模型为

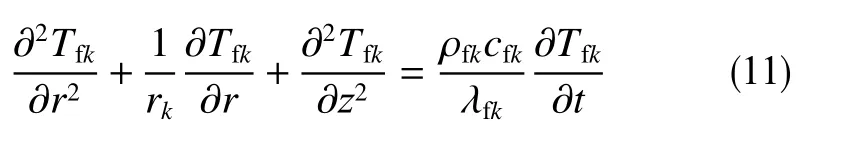
式中， λfk为套管/水泥环/岩石热导率，W/(m· ℃ )；ρfk为套管/水泥环/岩石密度，kg/m3；cfk为套管/水泥环/岩石比热容，J/(kg· ℃ )；Tfk为套管/水泥环/岩石温度，℃；k依据套管层级大小而定，4 ≤k≤ 11。

2.6 数学模型初始条件与边界条件

要对上述井筒-地层瞬态传热模型(7)～(11)进行求解，则要设置数值模型的初始条件和边界条件，其示意图如图2所示。

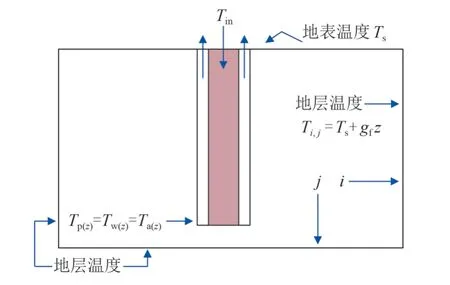
图2 初始条件与边界条件示意图Fig. 2 Schematic diagram of initial conditions and boundary conditions

2.6.1 模型初始条件

井筒-地层各控制区域包括钻柱内流体、钻柱壁、环空流体及近井壁地层初始温度与原始地温相等

式中，Ti,j表示钻柱内、钻柱壁、环空及近井壁地层温度，℃；θ为井斜角，°；i为井筒-地层径向各网格单元个数，1 ≤i≤ 11；j为轴向网格单元个数；Ts为地表温度，℃；gf为地温梯度，℃/100 m；z为井深，m。

钻柱内流体在井口的温度为钻井液入口温度

式中，Tin为钻井液入口温度，℃。

2.6.2 模型边界条件

钻柱内钻井液、钻柱壁及环空钻井液在井底处温度均相等，即

在井壁面，流出地层和传入环空的热量相等

流体循环未扰动远处温度，即离井壁远处的地层温度为原始温度

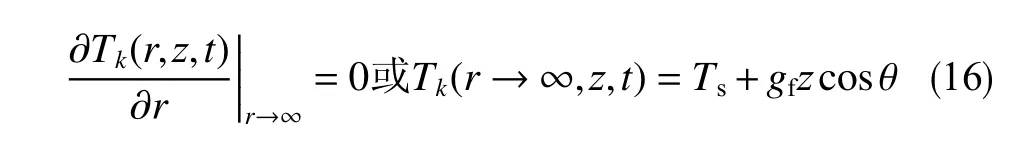
井筒-地层各控制区域在地表与大气为绝热状态

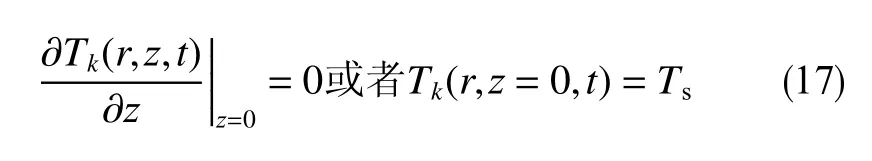
3 数值模型求解

上述井筒-地层瞬态传热模型为多个偏微分方程，可采用全隐式有限差分法对数学模型求解，模型离散格式为

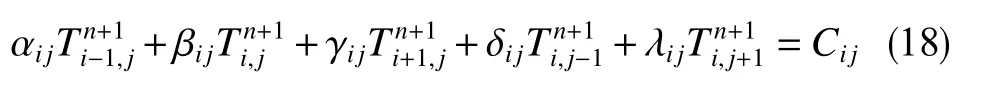
把所有节点的有限差分方程用矩阵形式表述，有

式中，αij、βij、 γij、 δij、λij、a分别为矩阵系数；i,j分别为在径向和轴向上空间网格节点；n为时间节点。

结合式(18)和式(19)离散形式，以含有复杂的二阶偏导的钻柱壁传热模型，即式(8)为例进行离散与合并，表达格式为

式中，T0、T1、T2分别为钻柱内流体、钻柱壁及环空流体温度，℃。

4 应用实例

4.1 基本参数

以四川盆地Y101H26-1井为算例，井身结构如表1所示。造斜深度为3700 m，水平增斜入靶A点井深为4125 m，井眼曲率为6.06 (°)/30 m。地表温度25 ℃，地温梯度3.1 ℃/100 m，排量29 L/s，油基钻井液密度2.17 g/cm3，钻井液动切力、稠度系数和流性指数分别为12.78 Pa、0.33 Pa· sn、0.81。

4.2 井筒-地层温度分布特征

图3为循环10 h时井筒-地层温度分布，可以看出，循环10 h时下部井段流体温度低于原始地层温度，而上部井段流体温度高于原始地层温度，该现象表明钻井液循环将下部井段热量携带至上部井段，导致流体冷却下部井段近井壁地层，加热上部地层。图4为近井壁地层温度与环空温度差分布图，可以看出，离井壁越远的地层，地层温度与环空温度差越大，在离井壁约1.079 m和2.844 m的距离，两者差值最大，则表明流体循环对近井壁扰动的距离约为1.079 m。该井造斜点深度为3700 m，至靶点A的井深为4125 m。在造斜点深度至靶点A，原始地层温度随井深呈非线性变化，至靶点A后，原始地层温度不变，该温度变化趋势与井斜角相关，如公式(12)和(16)所示。在增斜段，管内与环空截面积未发生变化，流体流经该区域产生的热对流交换热量与该段若为直井段相等，但增斜段，原始地层温度随井深增加而减小，流体流经该区域时在相等的对流交换量条件下，该段温度降低较多，导致造斜井段地层温度与环空温度差异最大；随着水平段延伸距离的增加，环空流体温度与地层温度之间的差值逐渐减小。

图3 循环10 h时井筒温度分布Fig. 3 well temperature distribution after 10 hours of circulation

图4 循环10 h时近井壁地层温度与环空温度差分布Fig. 4 Distribution of temperature difference between formation near well and annular space when circulating for 10 hours

4.3 井筒温度敏感因素分析

井筒温度影响因素较多，分析各因素对井筒温度的影响，为井筒降温提供技术指导。为此分析了循环时间、入口温度、钻井液比热容、钻井液密度及排量对井筒温度的影响。

图5为不同循环时间环空温度分布，可以看出，在井底循环初期(0.5、1、5 h)环空温度高于原始地层温度，其结果与常规直井循环温度不同(直井时，流体循环温度低于原始地温)。该现象由于在靶点A至靶点B的长水平段，井筒-地层的初始温度均为原始地温，不随井深发生变化。钻柱内流体从下至上和环空流体从底部向上流动过程中温度保持不变(直井时钻柱内流体从下至上流动时，在单位长度dz井段，流入的冷浆降低了该段流体的温度，使得循环流体温度低于地温)，同时流体循环产生流动摩阻，该流动摩阻在单位时间内产生热量，如公式(3)，导致井底流体在循环初期高于原始地温，当长时间循环后，钻柱内的冷浆逐渐进入下部井段，使得环空流体温度逐渐低于原始地温。为此，增加循环时间可以有效降低井底温度。

图5 不同循环时间环空温度分布Fig. 5 Annulus temperature distribution under different cycle times

图6为不同入口流体温度下环空温度分布，可以看出，随入口温度增加，井底温度增加，入口流体温度20、35、50、65 ℃时，井底温度134.17、141.28、148.39、155.51 ℃。由于入口流体温度增加，增加了流体携带入井内的热量，使得井内温度增加。因此，为了降低井底温度，可以适当降低入口流体温度。

图6 不同入口流体温度下环空温度分布Fig. 6 Annulus temperature distribution at different inlet temperatures

图7为不同钻井液比热容下环空温度分布，可以看出，随着钻井液比热容增加，钻井液在单位时间内吸收地层热量越多(Q=cmΔt，单位时间吸收地层的热量与钻井液比热容、单位流体质量及时间成正比关系)，环空温度降低越快。比热容1600、1800、2000、2200 J/(kg·℃)时，井底温度为151.3、142.48、134.78、128.03 ℃。为此，若能采用高比热容钻井液体系，如油基钻井液替换成水基钻井液体系，则降低井底温度效果会提升。

图7 不同钻井液比热容下环空温度分布Fig. 7 Annulus temperature distribution under different specific heat capacities of drilling fluids

图8为不同钻井液密度下环空温度分布，可以看出，随着钻井液密度增加，环空温度降低。通过热量计算公式可知，单位时间内质量越大的流体，与地层间发生的热交换量越多，使得环空流体温度迅速降低。当钻井液密度为1.87、2.17、2.37 g/cm3时，井底环空温度分别为147.66、142.48、139.42 ℃。

图8 不同钻井液密度下环空温度分布Fig. 8 Annulus temperature distribution under different drilling fluid densities

图9为不同钻井液排量下环空温度分布，可以看出，随着排量增加，环空温度先降低后增加。造成该现象的原因为：尽管高排量提升了环空流体与井壁之间的对流换热效率，但同时增加了环空循环摩阻，导致热量增加。同时，井较深(深部地层为无穷大的热源)，流体在钻柱内向下流动过程中流到井底所需时间长，流体易被加热。此时大排量引起高摩阻与喷嘴压降产生的高热量，使得井底温度增加。当排量分别为20、25、29、32、34 L/s时，井底温度分别为141.03、140.31、142.48、145.77、155.37 ℃。

图9 不同排量下环空温度分布Fig. 9 Annulus temperature distribution under different displacements

4.4 现场实测分析

目前，常规旋转导向工具服役温度为135℃，Y101H26-1井采用了地面降温方法来降低旋转导向工具在井底的温度，进而延长该工具的服役时间及增加水平段钻进长度。图10为该井通过地面降温设备将入口温度控制在35℃时的环空温度分布。利用本文建立的瞬态传热模型计算表明：井深为4600、5100、5250、5350、5450、5550、5650、5750 m时，井底环空温度分别为108.16、122.12、125.98、128.47、130.89、133.25、135.54、137.77 ℃。在5650、5750 m测温分别为137.5、141.6 ℃，计算精度超过97.3%。该井通过地面降温后，钻进井深小于5650 m (水平段长度1525 m)时环空温度低于135 ℃。

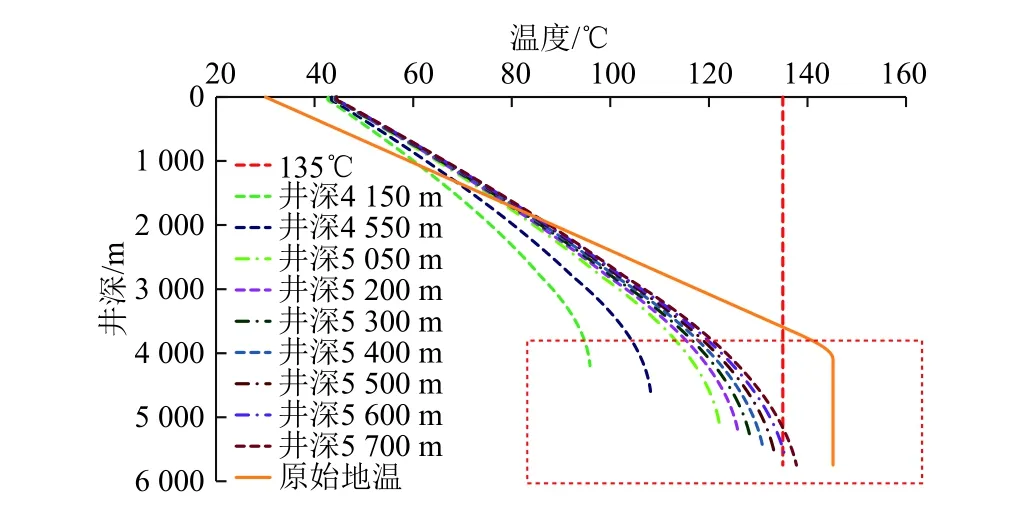
图10 入口温度为35 ℃时环空温度分布Fig. 10 Annulus temperature distribution when the inlet temperature is 35 ℃

结合上述模型计算预测精度，分析当不采用地面降温设备时，即入口温度为65 ℃环空温度分布特征，如图11所示。当井深为4600、5100、5250、5350、5450、5550、5650、5750 m时，井底环空温度分别为119.50、131.36、134.66、136.79、138.86、140.88、142.84、144.76 ℃。结合旋转导向服役环境温度，在5250 m时接近其服役环境。由图10和图11可知，通过地面降温设备将钻井液入口温度从65 ℃降至35 ℃，水平段钻进井深从5250 m延长至5650 m，延伸长度400 m，地面降温设备能有效降低井底温度，进而延长旋转导向工具服役时间。