基于介尺度PBM 模型的生物反应器放大模拟及实验研究

万景，张霖，樊亚超，刘勰民，骆培成，张锋，张志炳

（1 南京大学化学化工学院，江苏 南京 210023； 2 中国石化大连石油化工研究院，辽宁 大连 116045；3东南大学化学化工学院，江苏 南京 211189）

引 言

进入21 世纪，生物技术因资源可再生、环境友好等特点受到人们越来越多的关注。工业生物技术已成为世界各国争相发展的重点项目，其中生物反应器更是占据工业生物技术的中心位置。生物反应周期长、连续操作、效率低的特点导致了生物反应器具有高能耗、低设备利用率的缺点，因此高效节能的反应器成为科技与工程研发核心。由于生物反应器的设计和放大过程中存在着诸多困难[1-2]，大型生物反应器在设计初期很难通过实验的方式提供可靠的设计依据。而计算流体力学（CFD）技术可有效提供反应器内的流场、传质、传热等信息，因此利用CFD 相关软件进行数值模拟已成为大型生物反应器设计的重要途径[3-4]。

耦合CFD 与群体平衡模型(PBM)，涵盖了实际存在的气泡聚并、破碎等气泡动力学行为，从而可准确预测生物反应器内流场分布以及传质能力。随着对气泡动力学行为的深入认识，人们开发了多种气泡聚并与破裂的模型[5-6]。在气泡聚并模型方面，Luo 模型[7]被广泛应用于鼓泡塔模拟，但研究表明该模型会过高估计聚并频率，因此杨宁等[8-9]将气液体系内介尺度能量的描述和PBM 模型相结合，在气液体系稳定的状态下，介尺度能量趋于最小，与此同时，不同尺寸气泡的破碎和聚并状态达到平衡，故修正之后的模型能够更加准确地估计聚并频率。在气泡破碎模型方面，Luo 等[10]将能谱与涡能量相结合，他们认为涡不仅具有尺度，还具有能量，由此提出了湍流涡诱导碰撞气泡破碎的模型。Han 等[11]基于表面能量密度的增加提出了一种新型破碎依据，并将表面振荡和大尺度涡引起的破碎影响纳入模型；此外，Han 等[12-13]还改进了数学模型，使其能够适用于湍流的全能谱和气泡的多次破碎。Solsvik 等[14]的模型考虑了黏流剪切对气泡破碎的影响。Shi 等[15]提出了气泡诱导湍流的修正破碎模型，考虑了气泡诱导湍流影响下涡旋的平均湍流速度和对应的特征波数/长度尺度。

以上模型为模拟气泡聚并破裂的动力学行为提供了充分的理论基础，但是生物反应器内存在着湍流涡和气泡群介尺度结构，如何选择合适的模型阐明这种介尺度结构仍然面临巨大的挑战。本课题组在5 L 通气搅拌式工业生物反应器中通过组合不同聚并、破碎模型的方式，对八种模型组进行考察，分别从体积传质系数kLa和气泡尺寸两个方面与实验值对比，这八种组合模型包括以下四种诱导气泡碰撞的因素，它们分别为湍流涡随机运动诱导碰撞、浮升力差异诱导碰撞、大气泡的尾流夹带诱导碰撞和速度梯度差诱导碰撞。结果显示，与实验数据最为吻合的是基于介尺度理念的修正聚并模型与考虑黏流剪切的破碎模型组合。整个计算过程在商业软件Ansys Fluent 17.0 平台上进行。由于小型生物反应器的工业应用前景不大，故本文在选定最优气泡聚并破碎模型的基础上，通过叶轮末端剪切力相等的放大原则将5 L 生物反应器放大到400 m3。搅拌是化工生产过程中的重要环节，开发新型搅拌桨一直都是化学工程领域的热点[16-18]，本文通过软件模拟新开发了四种组合桨，考察不同桨型对生物反应器内气泡分散的效果，在分析了各个组合桨的流场特性、混合死区分布等特征之后，选出400 m3生物反应器的最优组合桨，为大型通气搅拌式工业生物反应器的设计与研究提供参考。本文组合气泡不同的聚并效率和破碎频率，得到了贴合实验值的气泡聚并破碎模型；并通过放大准则得到400 m3通气搅拌式工业生物反应器相关的结构和工况参数，进而使用最优聚并破碎模型模拟不同桨型的气泡分散情况。

1 实验装置与方法

1.1 实验装置

实验装置如图1 所示，该生物反应器外壁是具有椭圆封头的圆柱形玻璃材质，内壁有四块不锈钢挡板，挡板高232 mm，宽20 mm，厚度为3 mm。生物反应器内径T=150 mm，液面高度为298 mm，封头曲面高度30 mm。采用三层涡轮刚性桨，桨叶为不锈钢材质，桨叶直径D=50 mm,叶片长度17 mm，叶片宽度17 mm，叶片厚度2 mm，桨叶间距H0=70 mm，下层桨离底高度C=35 mm，气体分布器是内径为46 mm、宽度为12 mm 的不锈钢圆环，圆环上方等距离分布10 个直径为1 mm 圆孔，气体从中空的圆环通过圆孔向生物反应器喷出，生物反应器内设有溶氧电极，可间隔36 s记录氧气浓度。

图1 生物反应器实验装置Fig.1 Bioreactor experimental setup

1.2 实验方法

由于反应器内气相氧气浓度恒定，且假设混合过程是理想的，所以体积传质系数kLa的计算式[19]为

式中，CI0为初始溶解氧浓度；τp为DO 电极时间常数；CS为饱和溶解氧浓度；CI为实时溶解氧浓度。如果反应器的时间常数τR=1/kLa，远大于τp。则式（1）可简化为

因为饱和溶解氧浓度CS和初始溶解氧浓度CI0在整个实验过程中不会变化，故只需记录不同时刻t的实时溶解氧浓度CI，便可绘制函数-ln[(CS-CI)/(CSCI0)]的图像。由式(3)可知，kLa可通过函数-ln[(CSCI)/(CS-CI0)]对时间t求导得到。

实验开始前，先注纯水到生物反应器指定液位，校正溶氧值后开启搅拌（转速可调节200、300、400 r/min），打开连接氮气钢瓶的气体流量计，调节流量为4 L/min，通过溶氧电极记录体系中溶氧数据的变化；体系内的溶氧量会逐渐降低，待平衡后，停止通入氮气，打开氧气阀通入氧气，继续监测溶氧值的变化，每组转速重复3次实验，以此减少实验设备对结果的影响。通过高速摄像机(Phanton v2640)记录气泡信息，采集速度为1000 帧/秒，采集时间为30 s；得到气泡图像后，进一步处理得到气泡尺寸分布。

2 数学模型和数值模拟

2.1 控制方程

采用Eulerian-Eulerian 双流体方法进行三维数值模拟[20-21]。该方法将气相和液相分别视为分散相和连续相。两相滞留量满足相容条件

各相的连续性平衡方程为

各相的动量平衡方程为

2.2 相间作用力

根据Sanyal 等[22-23]的研究结果，本文模拟只考虑曳力，忽略其他相间作用力，曳力系数选择Schiller-Naumann模型[24]模拟气液体系相间作用力。

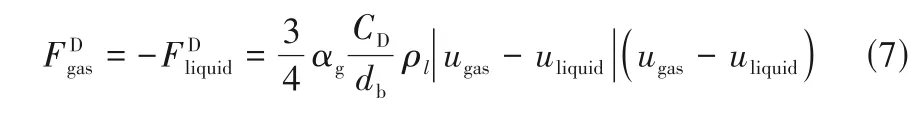
其中，曳力系数为

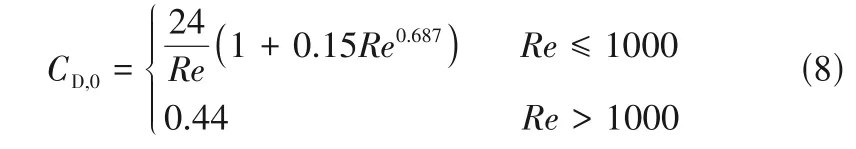
式中，CD是气泡群曳力系数;CD,0为单气泡曳力系数，CD=CD,0(1-αg)p，本模拟中p=1。

2.3 湍流模型

本文采用RNGk-ε湍流模型[25]来预测气泡塔内流体的流动特性。方程为

其中

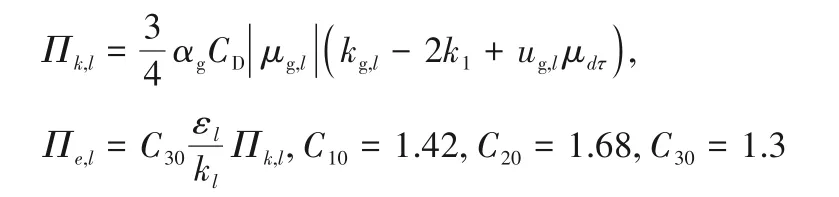
式中，Пk,l和Пe,l表示考虑气泡诱导湍流的源项。

2.4 群平衡模型

2.4.1 聚并模型 气泡聚并速率通常采用Luo 模型[7]，为

湍流波动引起的气泡碰撞频率[26](Prince and Bl)为

Luo[7]提出的聚并效率模型为

杨宁等[8-9]将气液体系内介尺度能量的描述和PBM 模型相结合，气液体系在稳定状态下，介尺度能量趋于最小，同时不同直径之间的气泡破碎和聚并处于动态平衡，从而提出了对聚并模型的修正方法。其中Luo 聚并模型[7]对应修正因子关系式见式（13）。

本文所研究的聚并模型如表1所示。

表1 本文研究的聚并模型详细信息Table 1 Details of the coalescence model studied in this paper

2.4.2 破碎模型 体积为V0的母气泡破碎成fV和(1-fV)V0两个子气泡的破碎率[27]为

式中，λ为涡旋大小；d0为母气泡直径；fV为破碎体积分数。

Luo等[10]提出的碰撞频率模型为

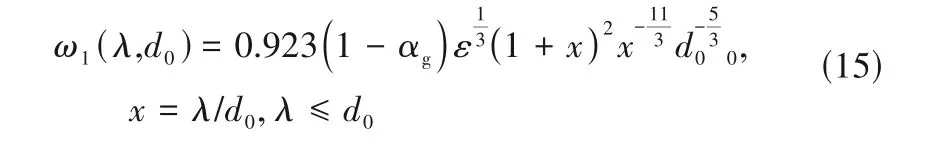
由Han 等[11]提出的模型中气泡与小涡(λ≤d0)和大涡(λ>d0)的碰撞频率为

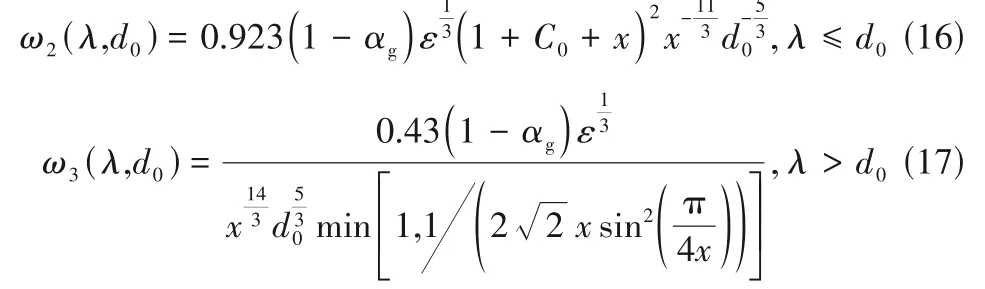
式中，C0为无量纲振荡比。

黏性剪切引起的碰撞频率由Solsvik等[14]提出的模型计算。

由Shi 等[15]提出的破碎模型考虑了在气泡诱导湍流影响下涡流的平均湍流速度和对应于BIT 的特征波数/长度。

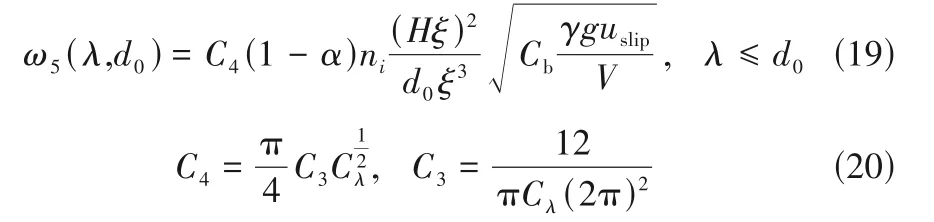
破碎概率为

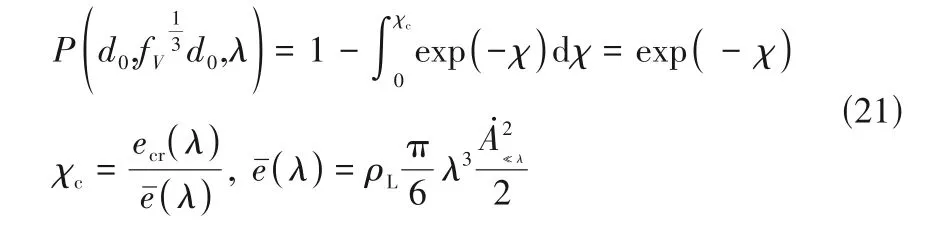
式中，χc为破碎的临界无量纲能量；eˉ(λ)为涡的平均动能；ecr(λ)为破碎所需临界涡的动能。

本文所研究的破碎模型的详细信息见表2。

表2 本文研究的破碎模型详细信息Table 2 Details of the crushing model studied in this paper

2.5 气泡直径和体积传质系数

在采用PBM 方法预测气泡尺寸分布时，利用class method(CM)对气泡进行离散，根据直径大小可将气泡分成若干组。界面面积a由气含率αg和Sauter平均直径(d32)求得

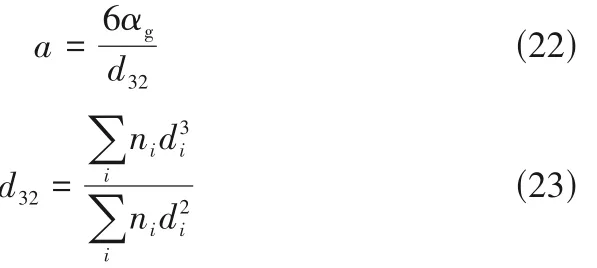
文献提出了很多计算体积传质系数kLa的方法，其中渗透理论[28]和表面更新理论[29]最常用。根据渗透理论，传质系数可描述为

式中，DL为氧分子扩散率，设为2.01× 10-5cm2/s[30]；ε为湍流耗散率；vl为液相运动黏度。

2.6 数值模拟

为了求解上述方程，本文采用耦合多网格求解器的有限体积格式对方程进行了“高分辨率”离散。搅拌槽的计算域划分为旋转叶轮域和静止域，在网格划分时采用较大的全局网格尺寸，并对叶轮旋转区域进行局部加密，保证计算精度。

本文采用四个网格尺寸，分别为501244、757201、1001872、1249354 个，来进行网格无关性验证。体积传质系数kLa及平均气泡直径d32是表征气液流动混合的重要参数。采用4种密度的网格得到的体积传质系数kLa及平均气泡直径d32数值模拟结果如图2 所示，由图可知，当网格数量增加到100 万个左右时，kLa和d32的数值模拟结果基本不变。因此，在随后的模拟中，均采用100万个网格尺寸作为计算基准。

图2 网格数量对模拟kLa和d32的影响Fig.2 Effects of mesh number on simulated kLa and d32

液面设置为Degassing 边界条件，搅拌桨设置为无滑移壁面，搅拌釜的外壁和挡板设置为静止壁面，初始气泡尺寸采用文献[31]中的方法计算。采用多重参考系法（MRF）进行稳态计算，气泡的聚并和破碎模型采用udf 编写，动量方程、体积分数以及湍流方程均采用一阶迎风格式离散，平衡状态为收敛残差低于10-5且进出口物料守恒。

3 实验结果与讨论

3.1 聚并和破碎模型对气泡尺寸模拟的影响

图3（a）分别为0、200、300、400 r/min 转速下拍摄的气泡图片。在同一位置进行多次拍摄，然后通过软件处理得到气泡尺寸分布。由图可知，随着搅拌转速的增加，气泡的尺寸明显减小且形状趋于球形。图3（b）为不同模型组合的平均气泡尺寸和实验测量值以及搅拌桨的剪切速率。由图可知，加入修正因子后，气泡尺寸会在一定程度上减小，相比其他破碎模型，B2 和B3 破碎模型预测的气泡尺寸更小，原因是这两种模型不仅考虑了传统的小涡引起的气泡碰撞，还考虑了大尺度湍流涡以及黏流剪切引起的气泡碰撞。在八组模型组合中，只有C2-B3（基于介尺度修正并考虑流体剪切的模型）最为接近实验值，而其他组合预测值的误差相对较大；在标准Luo模型中，随着转速的增加，搅拌桨剪切速率上升，对气泡的切割作用越显著，使得气泡直径越小，这与实际情况相吻合。四种诱导气泡碰撞的因素中，湍流涡随机运动诱导碰撞的影响最为显著，其他气泡组合模型无法准确地描述这种气泡行为，使得气泡聚并效率要高于实际值。本文C2-B3将气液体系内介尺度能量的描述和PBM 模型相结合，在气液体系稳定的状态下，介尺度能量趋于最小，与此同时，不同尺寸气泡的破碎和聚并状态达到平衡，故该模型能准确描述湍流涡随机运动诱导碰撞的影响，从而与实验结果吻合。

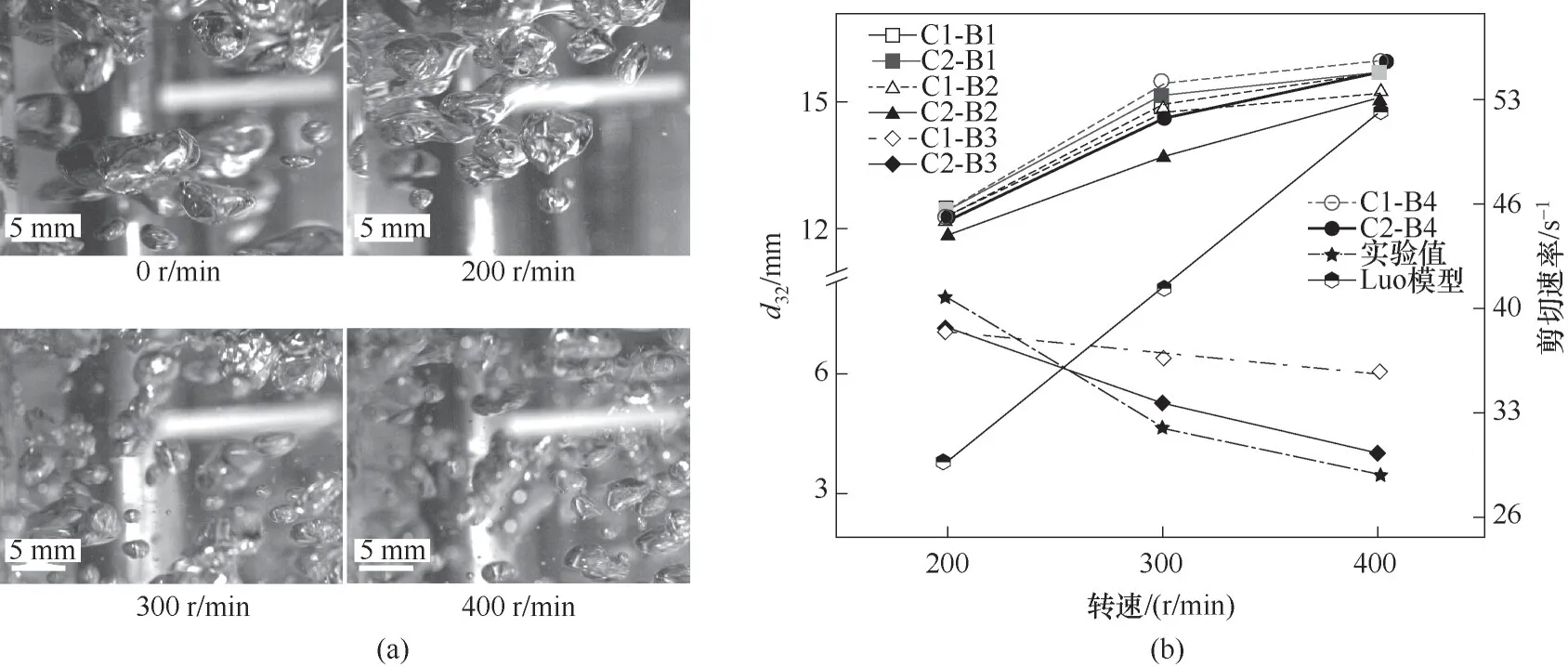
图3 0、200、300、400 r/min的气泡图(a);不同模型不同转速下的平均直径(b)Fig.3 Bubble diagrams at 0,200,300,and 400 r/min(a);Mean diameter of different models at different speeds(b)

图4 给出了最优模型组合下200、300、400 r/min转速的气泡平均尺寸分布云图。由图可得，转速为200 r/min 时，搅拌桨能够在一定程度上使其周围气泡破碎，但无法切割底部的大气泡；转速为300 r/min 时，大气泡数量明显减少，部分区域气泡尺寸更加均匀；转速为400 r/min 时，整个生物反应器内的气泡大小都比较相近，且气泡分布最为均匀。

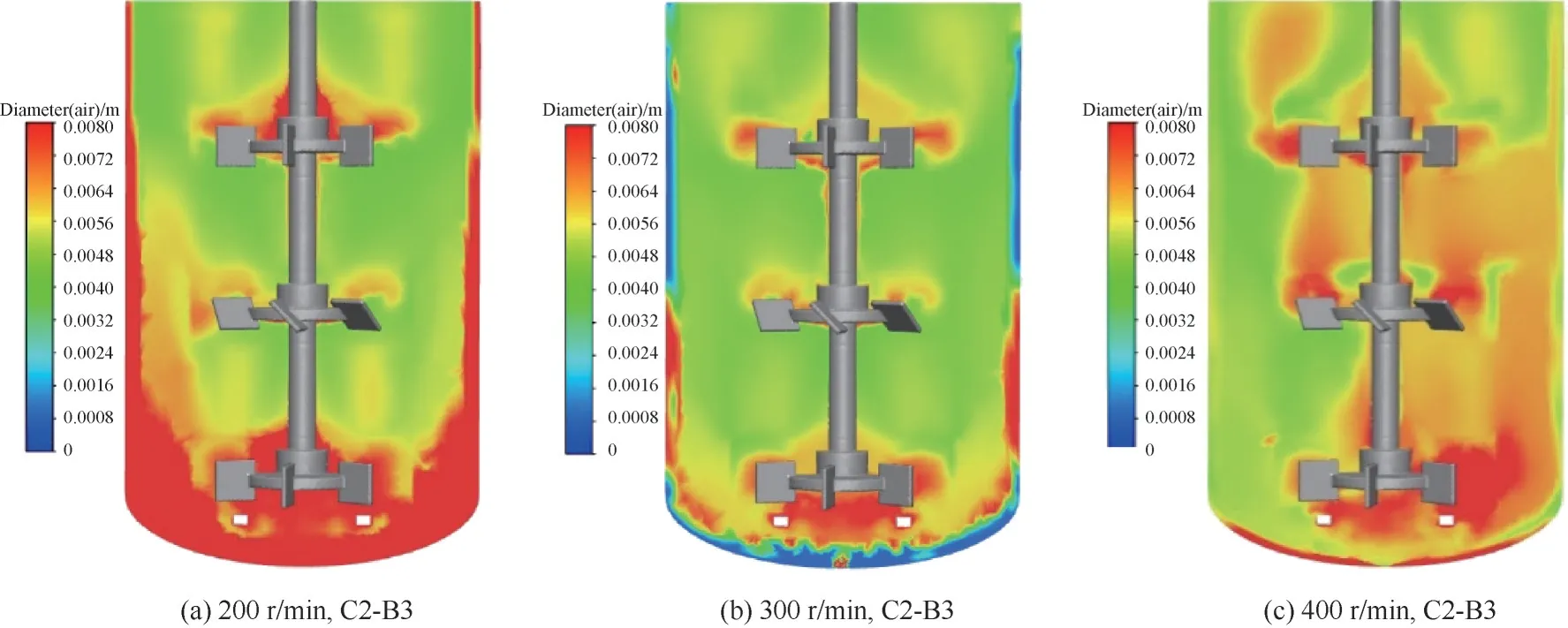
图4 最优模型组合下不同转速的气泡直径分布Fig.4 Distribution of bubble diameters at different rotational speeds under the optimal model combination

3.2 聚并和破碎模型对模拟体积传质系数的影响

图5（a）为生物反应器的溶氧率（DO 值）随时间的变化曲线，体系的通气量为1 m3/(m3·min)，搅拌转速为200、300、400 r/min。由图可知，随着氮气的通入，溶氧不断被吹出，导致体系内DO 值减小；当DO值到达最低点后改通空气，体系的溶氧逐渐增加直至饱和。此外，随着转速增加，体系内氧浓度的下降和上升都更加迅速。

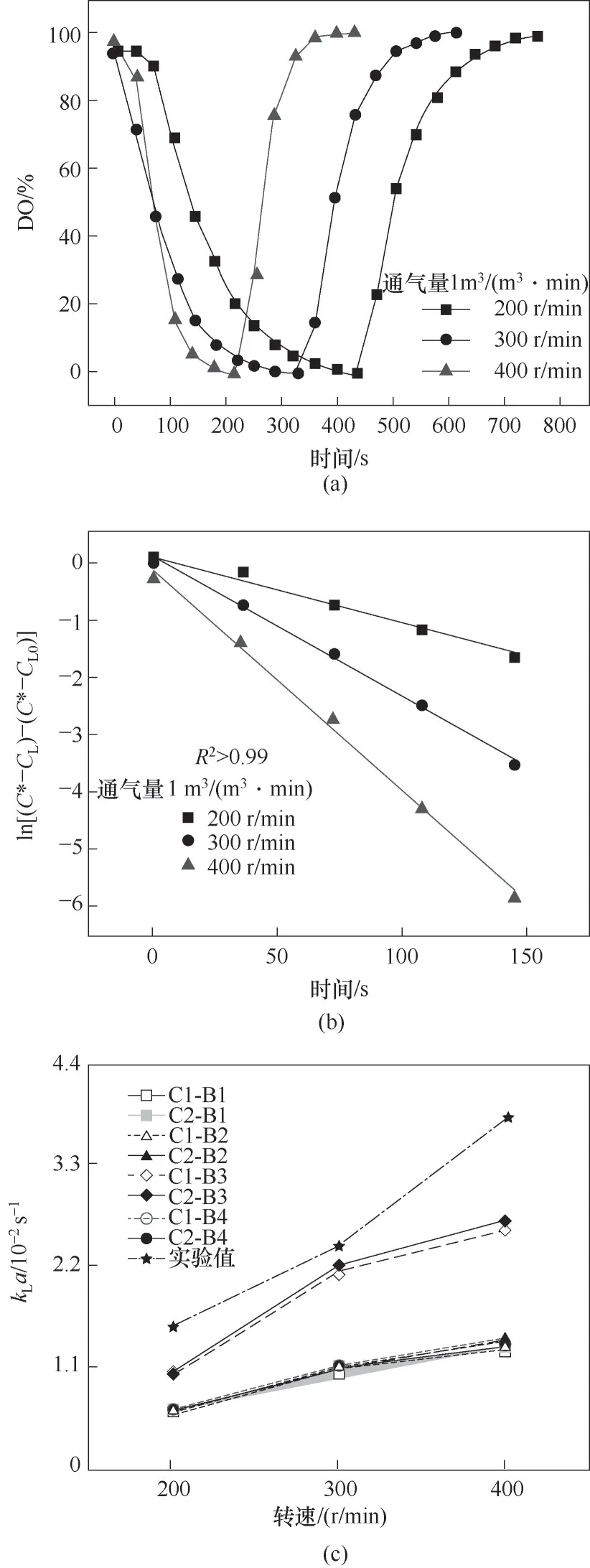
图5 DO值随时间的变化曲线(a)和拟合曲线(b)，不同模型组合在不同转速下的kLa(c)Fig.5 Variation curve(a)and fitting curve(b)of DO value with time，kLa of different model combinations at different speeds(c)

实验数据如表3 所示。在转速相同的情况下，三次实验得到的kLa都很接近，经过计算可得误差范围都控制在3%左右，这说明了实验测量的体积传质系数是可靠的。

表3 不同实验次数下kLa随转速的变化情况Table 3 kLa changes with speed under different number of tests

图5（c）为不同模型组合模拟的体积传质系数。由图可知，八种模型组合预测的体积传质系数均低于实验值，其中组合C1-B1 即文献中常用的Luo 聚并和破碎模型[7]与实验值偏差最大，组合C2-B3 模型与实验值最为接近，这与图3（b）气泡尺寸分布结果一致，因为根据式（22）、式（24），体积传质系数与气泡尺寸成反比。值得注意的是在相同破碎模型下，加入基于介尺度的修正因子能够降低聚并效率从而提高体积传质系数，这种修正效果在5 L 生物反应器中并不明显，这是因为5 L 生物反应器的表观气速较低，由式（13）可知较低的表观气速对应接近于1的修正因子。但是当该模型应用于大型通气搅拌式工业生物反应器时，其表观气速较大，这种修正效果将变得极为明显。此外，考虑黏流剪切的破碎模型将更适合于生物反应器的模拟，这是因为高速搅拌会造成极强的黏流剪切作用。图6为最优模型组合下体积传质系数分布云图，由图可知，kLa值大致呈现由中心向外壁逐渐降低的趋势，除此之外，一方面提高转速造成体系中气含率增大，kL增大；另一方面破碎气泡的作用也使得气泡尺寸变小，相际接触面积a增大，两方面作用下使得kLa值与转速成正相关。

图6 最优模型组合下不同转速的体积传质系数分布Fig.6 Distribution of volumetric mass transfer coefficients at different rotational speeds under the optimal model combination

3.3 400 m3 通气搅拌式工业生物反应器桨型的优化

在工业化生产中，为减少建筑成本和人工成本，工厂通常使用大型通气搅拌式生物反应器进行生物发酵，其中搅拌桨型对生物反应器效能而言至关重要，合适的搅拌桨型组合能使反应器内氧气的分布更加均匀，搅拌死区体积分数更小，从而缩短好氧生物的发酵时间，提高发酵效率。本文在设计大型生物反应器的罐体时，保持其与5 L 反应器几何相似，并微调高径比进行系列放大。400 m3生物反应器模型内壁有四块挡板，挡板高11.45 m，宽0.45 m，厚度为6 cm。生物反应器内径T=5.54 m，液面高度为12.5 m，封头曲面高度1.4 m。采用四层涡轮桨，桨叶直径D=2 m,叶片长度41 cm，叶片厚度2 cm，桨叶间距2.88 m，下层桨离底高度1.6 m，气体分布器是内径为1.56 m、宽度为33 cm 的圆环，圆环上方均匀分布着5 圈气孔，每圈有72 个直径为2 cm 的圆孔。生物反应器的放大准则分为单位体积功率相等、末端剪切力相等、单位体积传质系数相等。本文通过末端剪切力，即末端线速度相等的放大原则确定400 m3生物反应器的转速为50 r/min。

本文考察的轴流桨有六斜叶圆盘搅拌桨，径流桨有非对称式抛物线搅拌桨、布鲁马金式搅拌桨以及六直叶圆盘搅拌桨。将这些桨分为图7所示的四种组合[组合(A), 非对称抛物线式-六斜叶圆盘式-六斜叶圆盘式-非对称抛物线式搅拌桨;组合(B),非对称抛物线式-六斜叶圆盘式-六斜叶圆盘式-布鲁马金式搅拌桨;组合(C),六直叶圆盘式-六斜叶圆盘式-六斜叶圆盘式-布鲁马金式搅拌桨;组合(D),布鲁马金式-六斜叶圆盘式-六斜叶圆盘式-布鲁马金式搅拌桨]，综合对比生物反应器组合桨相应的气含率及kLa，可选择最优桨型。

图7 400 m3生物反应器桨型组合Fig.7 400 m3 bioreactor paddle type combination

如图8 所示，在相同工况下(50 r/min, 0. 3 m3/(m3·min))组合(A)、(D)对应的生物反应器底部存在近1/3 的死区，导致有效发酵空间减少；组合(C)对应的生物反应器虽然死区最小，但传质效果差，气泡分散效果不佳且生物反应器顶部气含率不高；组合(B)对应生物反应器的死区不仅较小，而且对气泡分散效果要优于其他三种组合。如图9 所示，组合（A）、（D）对应生物反应器的传质主要集中在搅拌桨周围，原因是该搅拌桨组合并不能很好地径向分散气泡，轴流效果明显大于径流效果，进而导致气泡主要集中在搅拌桨附近；组合(B)、(C)对应的生物反应器有较为明显的环流效应，搅拌桨对气泡的破碎效果较好，这导致平均体积传质系数高，且分布较为均匀。综上所述，组合(B)对应的生物反应器拥有搅拌死区体积分数小、平均体积传质系数高等特点，故组合(B)对应的搅拌桨为最佳桨型。

图8 400 m3生物反应器不同桨型气含率分布Fig.8 Distribution of gas holdup with different paddle types in a 400 m3 bioreactor

图9 400 m3生物反应器kLa分布Fig.9 kLa distribution of 400 m3 bioreactor

4 结 论

针对生物反应器内存在的复杂湍流涡和气泡群介尺度结构，本文以5 L 通气搅拌式工业生物反应器为对象，考察了基于介尺度提出的修正聚并模型以及四种气泡破碎模型对模拟流体流动行为以及气液传质能力的影响；后续通过叶轮末端剪切力相等的放大原则将5 L生物反应器放大到400 m3，在采用最优气泡聚并破碎模型的基础上对400 m3通气搅拌式生物反应器进行了搅拌桨型的优化，结论如下。

（1）气泡的聚并破碎模型对预测气泡尺寸分布有很大影响，最优气泡模型无论从气泡的数密度还是气泡所占体积两方面考察，所得模拟结果均与实验测量结果最接近。在气泡聚并模型方面，基于介尺度修正的聚并模型能够降低体系内气泡聚并效率，从而模拟的气泡尺寸和体积传质系数更加准确。聚并效率降低的程度因反应器尺寸的不同而有所差别，如在小型生物反应器中，加入修正对体系的影响并不显著，但是在大型生物反应器中，由于表观气速较大，这种修正效果将更加明显；在气泡破碎模型方面，B3破碎模型除了考虑传统的小湍流涡引起的气泡碰撞外，还考虑了黏流剪切引起的气泡碰撞，使模拟破碎效果与实际气泡破碎效果十分接近。综上所述，C2-B3（基于介尺度修正且考虑流体剪切的模型）预测的气泡尺寸和体积传质系数最贴合实验值。

（2）对于400 m3工业生物反应器，非对称抛物线式-六斜叶圆盘式-六斜叶圆盘式-布鲁马金式搅拌桨的组合形式具有氧传质能力强、死区体积分数小的特点，适合应用于大型工业生物反应器。