湍流系统的能量最小多尺度模型研究进展

王利民，郭舒宇，向星，付少童

（1 中国科学院过程工程研究所多相复杂系统国家重点实验室，北京 100190；2中国科学院大学化工学院，北京 100049）

引 言

过程工程中存在着不同尺度的湍流，其对物质传递与反应效率发挥着重要作用。自雷诺实验以来，湍流科学研究已有一个多世纪的历史[1]，但其仍为经典物理学中尚未解决的主要难题之一[2]。Reynolds将充分发展的湍流运动分解成时均运动和脉动运动，在对Navier-Stokes 方程进行雷诺分解时，产生了未知的雷诺应力项，造成了雷诺时均运动方程不封闭的根本性困难[3]。为了封闭雷诺时均运动方程，需要对雷诺应力项进行模化，而模化的方式可以多种多样，构造了各种湍流模型。

当前文献报道的湍流模型已达数百种。普遍认为，湍流模型的关键在于模型封闭的合理性。传统的湍流模型可分为两类[4]。第一类是涡黏法，假设湍流脉动对平均流有耗散作用，Boussinesq 假设下的雷诺应力在数学上类似于牛顿流体的应力-应变关系，并与平均应变率成正比。典型的涡黏模型主要有零方程模型[5]、一方程模型[6]和两方程模型[7-9]。涡黏性模型中，与分子理论中的平均自由程类似，Prandtl率先提出了混合长度模型[10]，通过引入湍流特征长度来模化雷诺应力，但该模型存在很多不足，在模型中特征长度的取值根据简单工况的实验确定，在应用到比较复杂工况时其适用性依然存疑；湍流场的尺度范围很大，用单一长度尺度来描述雷诺应力不合适。随后Taylor 的涡量输运理论、von Karman的相似性理论也通过假设雷诺应力和时均速度梯度之间的关系来封闭雷诺时均（Reynoldsaveraged Navier-Stokes,RANS）方程[11]。随着湍流建模和模拟技术的发展，这些唯象湍流模型逐渐被更复杂的模型所取代。由于湍流过程中有序和无序共存的复杂性，目前还没有一个公认的普适湍流模型。另一类是雷诺应力模型（Reynolds stress model,RSM）[12]或二阶矩闭合模型，该模型考虑了雷诺应力的各向异性和复杂的湍流相互作用，比涡黏模型更详细、更通用。Chou[13]和Rotta[14]在雷诺应力模型做出了开创性工作，直接从雷诺应力输运方程或其简化代数方程计算Navier-Stokes 方程中的雷诺应力张量，从而摒弃了湍流黏性系数的概念。然而这种建模方法中雷诺应力存在扩散输运、湍流压力-应变相互作用，以及产生项和耗散项等，仍存在封闭问题[15]。此外，由于雷诺应力的计算需要另外求解六个输运方程，使得RSM 的计算成本非常高。因此，与直接数值模拟（direct numerical simulation,DNS）[16]和大涡模拟（large eddy simulation, LES）[17]一样，RSM 产生的信息量远超工程中计算平均流动的所需，不具备成本效益[18]。

各种层次的湍流模拟方法如图1 所示，除DNS外均需要构建湍流模型。湍流模型是影响工程湍流模拟准确性的关键因素之一，在计算流体力学（computational fluid dynamics,CFD）模拟中起着关键作用。当前各种湍流模型形式千差万别，但封闭雷诺时均方程的方式仍是经验性的，缺乏对复杂流动的各种相互作用的竞争中协调及控制机制的深入研究。而介科学理论致力于阐明复杂系统中各种控制机制的相互作用，本文基于介科学框架，以能量最小多尺度(energy-minimization multi-scale,EMMS)的思想为核心，介绍了湍流中介尺度行为的共性原理，包括湍流中的黏性控制机制与惯性控制机制，以及二者在流动中的竞争中协调以实现稳定性条件。基于该思想构建了具备工程应用价值的EMMS 湍流模型，显著改进了RANS 模拟预测的精度，在层湍转捩预测以及全球气候仿真等具备重要应用价值，为介科学理论作为复杂系统的普适理论奠定了基础。

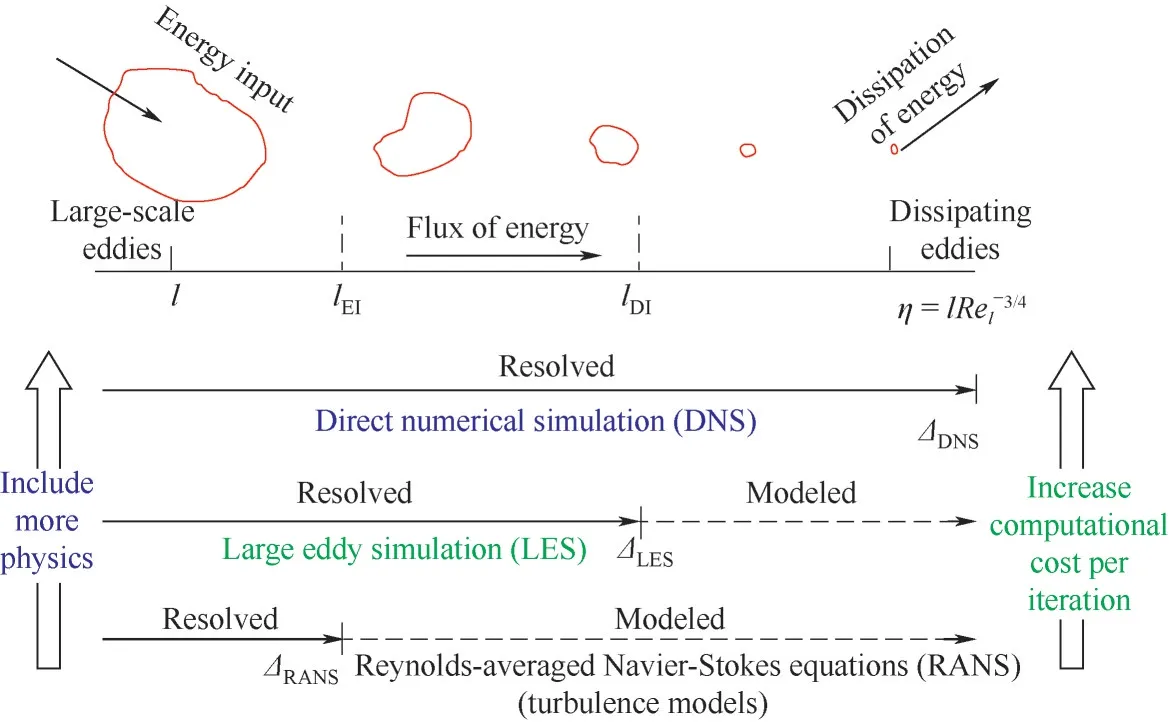
图1 湍流模拟的通用多尺度框架Fig.1 A generic multiscale framework for modelling turbulent flows

1 EMMS建模思路

20 世纪80～90 年代，李静海等[19-21]从气固流态化中的颗粒聚团现象出发，认为：气体和颗粒都拥有自己独立的运动趋势，即气体趋向于选择阻力最小的途径流动，而颗粒总是尽可能处于最小位能的位置，介尺度聚团的形成源于气体和颗粒的各自运动趋势在竞争中的协调。李静海等原创性地提出了基于颗粒尺度、颗粒聚团尺度和设备尺度的多尺度分析方法和介尺度聚团结构应满足的稳定性条件，将该稳定性条件与气体、固体的守恒方程和团聚物尺寸方程同时求解，从而得到相应的结构参数，建立了具有普遍意义的EMMS 模型[19-21]。EMMS 模型成功实现了非均匀气固系统的准确模拟，显著提升了预测的准确性和精度[22-23]。邱小平等[24]耦合了EMMS 曳力与简化双流体模型，实现了工业规模气固反应器快速模拟的潜力。陈恺成等[25]开展了基于EMMS 的循环流化床流域研究，确定了快速床的操作边界。佟颖等[26]基于双分散颗粒EMMS 曳力模型，模拟了两种不同的双分散鼓泡流化床，探讨了模型的适用性。

EMMS 原理成功推广到其他复杂系统[27-28]。在气液体系中，应用EMMS模型能量分解的基本思路，Ge等[28-29]对气液体系微观和介观能耗过程进行了区分和定义，提出了气液体系的稳定性条件。在此基础上，Yang 等[30]假设鼓泡塔体系中存在两种气泡特征直径，以反映体系内的非均匀结构，提出了双气泡(dual-bubble-size, DBS)模型，从理论上预测了鼓泡塔中的流型转变，在结构参数范围内，全局微尺度能耗最小值对应的解会发生跳跃，从物理上解释了流动结构的宏观演化。Han 等[31]根据介区域分析了主导机制，并基于介尺度框架研究了鼓泡塔中的流域转变。陈卫等[32]将流态化过程中鼓泡、湍动和快速流化过程类比物质的固、液和气三态，尝试基于EMMS 原理构建相变理论。马永丽等[33]对气液固流化床内复杂三相流动结构的介尺度机理模型进行了分析和总结。汪帆等[34]基于介尺度研究范式及理论，探讨了利用EMMS 模型对现有成核数学模型进行修正和优化的思路。

上述研究的非平衡复杂系统都遵循控制机制之间的竞争中协调，文献中的大量模拟和实验结果都证实了EMMS原理对所研究非平衡复杂系统的适用性[35-37]，表明了EMMS 模型背后蕴含的原理具有一定的普遍性。EMMS建模思路从理解复杂系统的多尺度结构和不同机制之间的相互作用和控制机制开始，通过分析各控制机制的竞争中协调获得系统的稳定性条件，在数学上可表述为多目标变分问题。因此，通过相应的稳定性条件和复杂系统的封闭模型，可以实现不同尺度下动力学方程的关联[38-39]。经过三十多年的努力，EMMS思路已经成为解决复杂系统问题的一个非常有前途的工具，这一原创性学术思想形成了创新性的EMMS原理与介科学理论体系[40]。

2 湍流控制机制与稳定性条件

雷诺实验通过临界Reynolds数来区分流动的层流和湍流状态，率先开展了流动稳定性的研究。Heisenberg[41]将Orr-Sommerfeld 方程用于分析平面Poiseuille 流的稳定性，发现在接近湍流起始流速的有界剪切流中会出现Tollmien-Schlichting 波，该方法也被用于解决流动稳定性问题[42]。Lorenz[43]发现，流体确定性模型的所有非周期解均有界但存在不规则的波动，这与控制方程非线性导致的无穷多序列分叉和扰动有关。Helmholtz[44]提出了恒定外力作用下流体缓慢稳定流动的最小能量耗散率原理。Korteweg[45]发现层流状态下流体的流动分布使得黏性的能量损失最小。Reyleigh[46]将最小能量耗散率原理扩展到许多其他流体流动系统。根据非平衡热力学理论，Bejan[47]提出了层流中最小熵产生原理，这与最小能量耗散率原理一致。

一般认为，在层流中，系统完全由流体黏性决定，速度分布受黏性耗散率最小的条件控制。而在单相湍流中，黏性控制机制和惯性控制机制共同作用，比层流中黏性作用主导的情况要复杂很多，因此Helmholtz[44]提出的最小能量耗散率原理不再适用于湍流。

目前，基于各种最大化流动耗散函数，提出了几种变分准则来预测单相湍流中的平均速度场。Malkus[48]提出了最大总黏性耗散率D的变分准则，以预测湍流管流中的轴向速度分布。随后，该准则被修正为最大“效率”E=DDf/Dm（这里Dm是平均流的黏性耗散率，Df=D-Dm是脉动的耗散率），由最大“效率”E预测的最佳速度场比最大总黏性耗散率D得出的结果更接近实际流动[49]。Bertram[50]提出了一种新的最小湍动能变分判据，并试图阐明不同变分判据在不同约束条件下的联系。自Malkus 的最大总黏性耗散率D变分准则出现以来，湍流系统中出现了各种变分原理，但均无法解释为什么一些变分原理可以产生实际结果。此外，对于给定最大/最小化的特定流动量缺乏明确的物理基础。

由于单相湍流系统中存在黏性和惯性两种不同的控制机制，变分原理不能仅用黏性控制机制的极值趋势或惯性控制机制的极值趋势来表示；相反，这两种控制机制的竞争中协调对系统稳定起着重要作用。如果认为单相湍流由许多湍流涡组成，且涡与周围环境的相互作用类似于颗粒和气体之间的相互作用，则湍流系统和气固系统的耗散行为类似[27]。黏性和惯性控制机制都不能完全支配一个系统，因此它们不能完全实现各自的趋势；相反，它们通过竞争中协调来共同实现系统稳定。Li等[27]发现了黏性控制机制和惯性控制机制之间的竞争中协调，类似于气固系统中颗粒主导机制和气体主导机制之间的竞争中协调，提出黏性耗散率Wv最小和总耗散率WT最大，即

利用关系式(1)作为稳定性条件成功预测了圆管湍流的径向速度分布。Wang 等[28,51-52]发现，湍流中黏性力和惯性力分别反映了速度场在空间和时间上的非均匀性。惯性力和黏性力同时作用于流体微元，流体微元提供载体，黏性和惯性在流体微元内竞争中协调，其中惯性机制和黏性机制均与耗散有关。将总能量耗散分解为平均剪切耗散和湍流脉动耗散：

式（2）右侧第一项为平均剪切耗散，定义为Wv；第二项为湍流脉动耗散，定义为Wte。假设Wv与完全层流中能量耗散的本质相同，由黏性占优，则根据最小黏性耗散原理，与时均速度场相关的平均剪切耗散Wv应趋于最小。

当流动处于稳定状态时，流体微元受到的惯性力为：

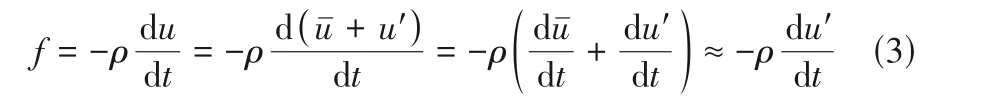
即表明流体的脉动决定其惯性运动，湍流脉动越剧烈则惯性作用越强。湍流惯性机制与湍流脉动的耗散存在密切关联。根据Li等[27]认为总耗散率WT趋于最大，由于黏性作用使黏性平均剪切耗散率Wv趋于最小，所以湍流脉动耗散Wte=WT-Wv趋于最大，这样可推导出如下关系：

建立合理湍流模型的关键在于如何更深刻地理解计算网格中的湍流结构，而这与稳定性条件密切相关。如果不考虑这种稳定性条件，很难开发出更好的模型。EMMS 湍流模型考虑稳定性条件，利用式(4)进行封闭湍流动力学方程。

3 EMMS湍流模型

工程中的湍流主要表现为层流和湍流共存。然而传统的湍流模型假设流体在计算网格中处于均匀和充分湍流状态，从而忽略了流动中的层流部分，导致工程中实际流动的湍流模拟并不精确。湍流模拟中，面对计算网格内的非均匀性，通常采取的方法为平均化处理、通过滤波只解析大涡和解析所有尺度的涡结构，而忽视了湍流中的介尺度涡团及黏性和惯性之间竞争中协调的主导机制，因而难以同时兼顾模拟的准确性和计算量。

3.1 EMMS湍流模型的建立

在由不同大小“旋涡”组成的单相湍流中，存在多尺度结构和复杂的相互作用[11]。湍流中涡的运动在空间尺度和时间尺度上是动态耦合[53]，由于大涡并不稳定，最终会分裂成许多小涡，伴随着湍动能由大涡向小涡传递。众多小涡继承了前一个旋涡的能量，经历同样的过程分裂成更小的涡，再将能量向下传递。通过这种方式，能量从大的运动尺度一直传递到足够小尺度。

微尺度：范围从分子尺度到Kolmogorov 尺度η，该尺度下黏性和惯性交替变化。当黏性占主导，一组分子作为一个整体进行相同的运动；而当惯性占主导时，考虑两个旋涡之间的界面高速剪切作用。

介尺度：一定范围的涡代表湍流的介尺度结构。湍流惯性子区尺度(η≪l≪L)远大于Kolmogorov 尺度，但远小于宏观的流动尺度。介尺度涡从大尺度涡的波动中获取动能，并将其传递给更小的涡。介尺度涡可看作是将大尺度含能涡与小尺度耗散涡联系起来的桥梁。

宏尺度：包含大尺度流体的流动，L。大尺度流动受边界特定的几何特征控制，因而是各向异性的。大多数大尺度波动从平均流接收能量，并将其转换为小尺度波动。宏尺度包含了尺度范围内涡的大部分动能。宏观尺度涡的作用是从主流获取能量以维持湍流。因此，宏尺度行为体现在与壁面和边界效应相关的全局波动。

随着EMMS模型和DBS模型在气固和气液两种系统中的成功发展，EMMS 建模思路扩展到了单相湍流体系[52,54]，即EMMS湍流模型（图2），其使用了稳定条件来封闭湍流。具体来说，视流动为由湍流流体相和非湍流流体相组成的两相流问题，引入描述该两相流系统的介尺度结构参数，特别是湍流流体成分所占的体积分数，使湍流有效黏性系数进一步增强所含的湍流介尺度结构信息。随后，根据湍流涡级串理论，将湍流中包含的能量耗散分解为不同部分，然后进行量化，与气固系统EMMS模型的原理类似，通过惯性和黏性协调控制机制形成的湍流稳定性条件封闭湍流模型，优化出湍流的介尺度结构参数，改进湍流模式理论中的涡黏性系数。

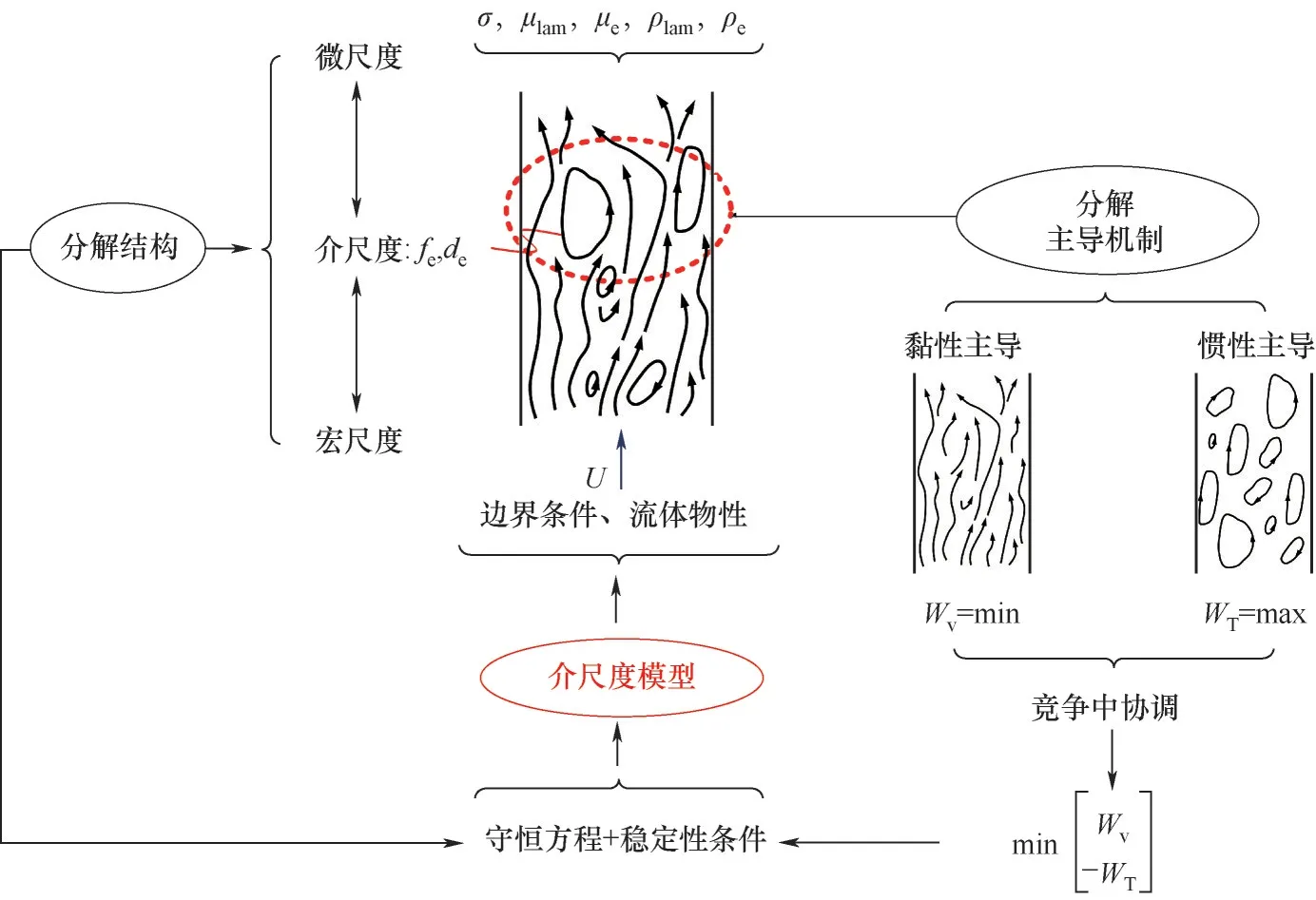
图2 湍流系统的介尺度框架[52]Fig.2 A mesoscale framework for turbulence system[52]

3.1.1 流动分相与对应的约束方程 最新发展的双涡EMMS 湍流模型[55]借鉴两相相互渗透的双流体模型，假设在流动中具有层流流体成分、大涡流体成分和小涡流体成分组分（图3）。则该系统可通过下述结构参数来描述：层流、大涡和小涡的体积分数（fl，fL和fS）；大涡和小涡对应的等效直径（dL和dS）；层流、大涡和小涡的表观速度（Ul，UL和US）。

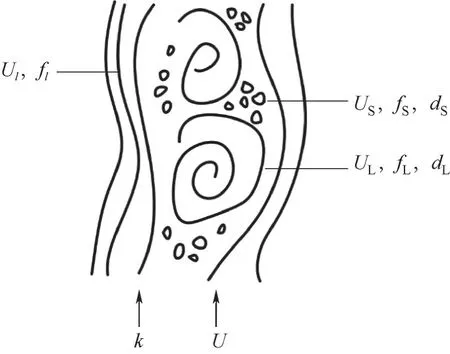
图3 双涡EMMS湍流模型结构示意图[55]Fig.3 Structure diagram of dual-eddy EMMS-based turbulence model[55]

当流动处于稳定状态时，涡团所受的曳力和有效浮力相平衡，大、小涡团的力平衡方程分别如下：

其中，g是重力加速度。大、小涡团和周边层流流体之间的滑移速度分别为：

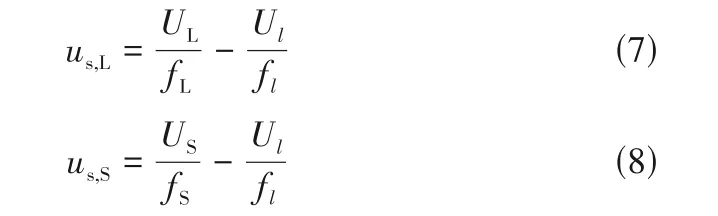
本模型通过将涡团类比于气泡，从而得到其曳力系数。大涡的曳力系数计算公式如下：

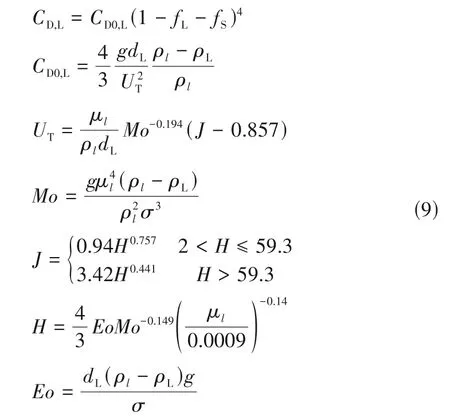
小涡的曳力系数可以根据式（9）以此类推计算而得。

假设求解范围内的所有湍动能k均由大涡贡献，其湍流强度为终端湍流强度I0，则大涡的特征方程表示为：

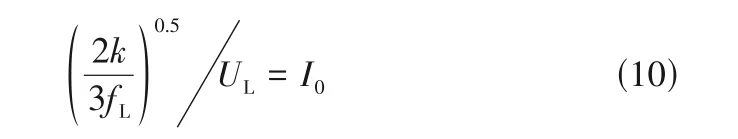
由耗散涡Reynolds数约为1可得：

此外，流体速度和相体积分数的守恒方程分别为：

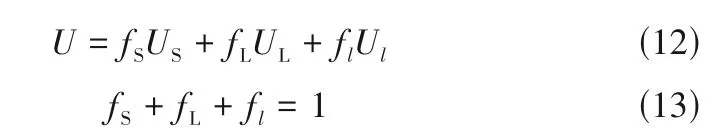
3.1.2 能耗分解 假设流体流动处于稳态，则总能量耗散率WT等于能量输入率，可分解为四个部分：湍流涡团与周边流体表面互相振荡而引起的能量耗散率Ws，大尺度涡团破碎而产生的能量耗散率Wbk，耗散涡尺度的小涡能量耗散率WKolmogorov，以及发生在层流（非湍流）成分流体内的分子黏性耗散Wv。根据上述描述得到方程：

WT可近似为初始大涡的能量耗散率：

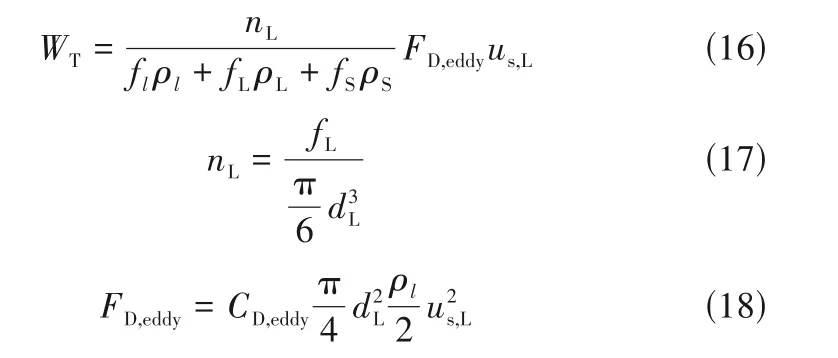
Ws与湍流涡团表面的剧烈振荡而引起的阻力FD,surf有关：

Wbk可写成如下形式：

其中,ωL,λ(dL,λ)为抵达频率；PL͂(dL|fBV,λ)为碰撞破碎的概率密度分布函数；dL为被撞击的涡团尺度；λ为撞击的涡团尺度；EDIS为涡团破碎时的黏性耗散。

WKolmogorov根据均匀各向同性湍流的耗散谱计算得出：

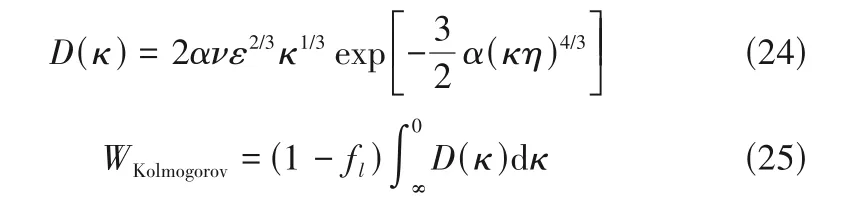
通过输入U、k、σ、μl、ρl、ρL、ρS求解以上代数方程，结合式(4)即可优化得到该工况下的层流体积分数、层流速度、大涡体积分数、大涡速度等一系列结构参数。

3.2 EMMS湍流模型与CFD耦合

双涡EMMS 湍流模型假设在一般湍流中有层流、大涡和小涡三部分共存，并相互渗透。在CFD求解RANS 方程中，首先获得计算网格中的流体速度U和湍动能k，通过求解EMMS湍流模型即可获得该网格单元下的结构参数fL，fS，fl。基于大涡体积分数fL对RANS 模型中的湍流黏性系数进行修正。以耦合RANS方程中的k-ωSST模型为例，湍流黏性系数μt被修正为：

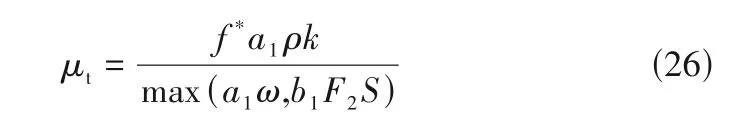
即将控制方程中的μt乘以由fL归一化得到的湍流控制因子f*，同时，k方程中的湍动能生成项也需要乘以f*来抑制湍动能在局部区域的生成。基于EMMS模型的计算结果，f*已拟合为代数形式：

3.3 EMMS模型显著改进了预测精度

基于EMMS 原理的湍流模型显著提高了RANS在湍流建模和仿真中的精度[56]。例如，在顶盖方腔流中，EMMS 湍流模型可以成功捕捉到左下角和右下角的三次角涡，而标准的k-ε模型无法预测(图4)。此外，EMMS 湍流模型预测的流线相比于标准k-ε模型预测的流线更符合DNS结果[52,54]。

图4 基于EMMS的湍流模型预测的Re=10000时顶盖驱动方腔流的流线图与DNS和k-ε的流线比较[52]Fig.4 Streamline patterns for lid-driven cavity flow at Re=10000 predicted by the EMMS-based turbulence model in a comparison with those from DNS and k-ε model[52]

边界层转捩预测在高速飞行器的设计中起着重要作用[57]。与CFD 发展的其他领域相比，转捩区的CFD 预测仍然是一个难点。RANS 方法用于预测转捩问题具有计算成本低的优势[58]。文献[59-61]中报道了RANS 下三种计算层流到湍流转捩的方法：(1)在实验确定的转捩位置打开湍流模型或使用湍流黏度；(2)利用低Reynolds 数湍流模型；(3)使用间歇的概念来混合从层流到湍流区域的流动。这些方法大多缺乏真实的物理基础，适用范围相当有限。

为了耦合CFD 进行计算，基于OpenFOAM 进行了二次开发，构建EMMS湍流模型库、不可压缩湍流模型动态库和可压缩湍流模型动态库。基于双涡EMMS 湍流模型优化湍流体积分数f，并与k–ωSST湍流模型耦合[9]，实现了平板及NACA0012翼型边界层转捩的预测，结果如图5 和图6 所示。算例计算网格与边界条件如图7 和图8 所示。f*由0 逐渐增大到1表明流体微元由完全层流控制逐步转变为完全湍流控制。图9 和图10 分别为平板和翼型边界层的表面摩擦系数，Cf突增的点即为转捩位置，与图5 和图6 中f*突变的位置相对应，且均与实验数据[62-63]吻合较好，验证了双涡EMMS 湍流模型预测转捩问题的可行性。

图5 平板边界层转捩算例的湍流控制因子f*分布[55]Fig.5 Turbulence control factor distribution for flat plate boundary transition case[55]

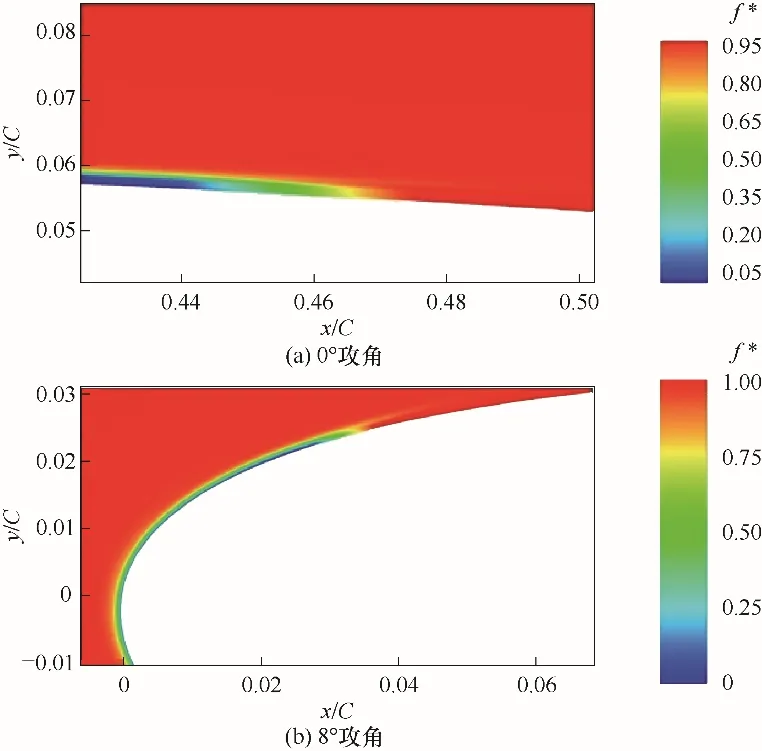
图6 NACA0012翼型上表面转捩点附近湍流控制因子f*分布Fig.6 Turbulence control factor distribution near transition point on the NACA0012 top-surface

图7 T3A 算例计算网格与边界条件Fig.7 Computational mesh and boundary conditions for T3A case

图8 NACA0012翼型算例计算网格Fig.8 Computational mesh for NACA0012 airfoil case

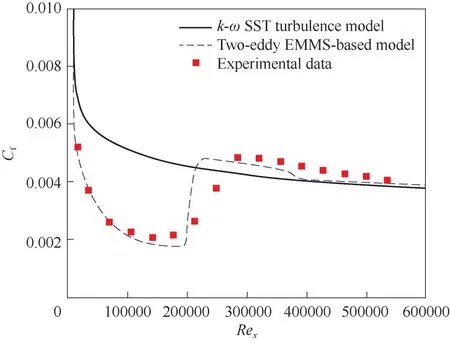
图9 双涡EMMS湍流模型和k-ω SST湍流模型预测平板边界层表面摩擦系数Cf及与实验数据的比较Fig.9 Skin friction Cf predicted by two-eddy EMMS-based turbulence model and k-ω SST turbulence model in a comparison with experimental data on the flat plate boundary

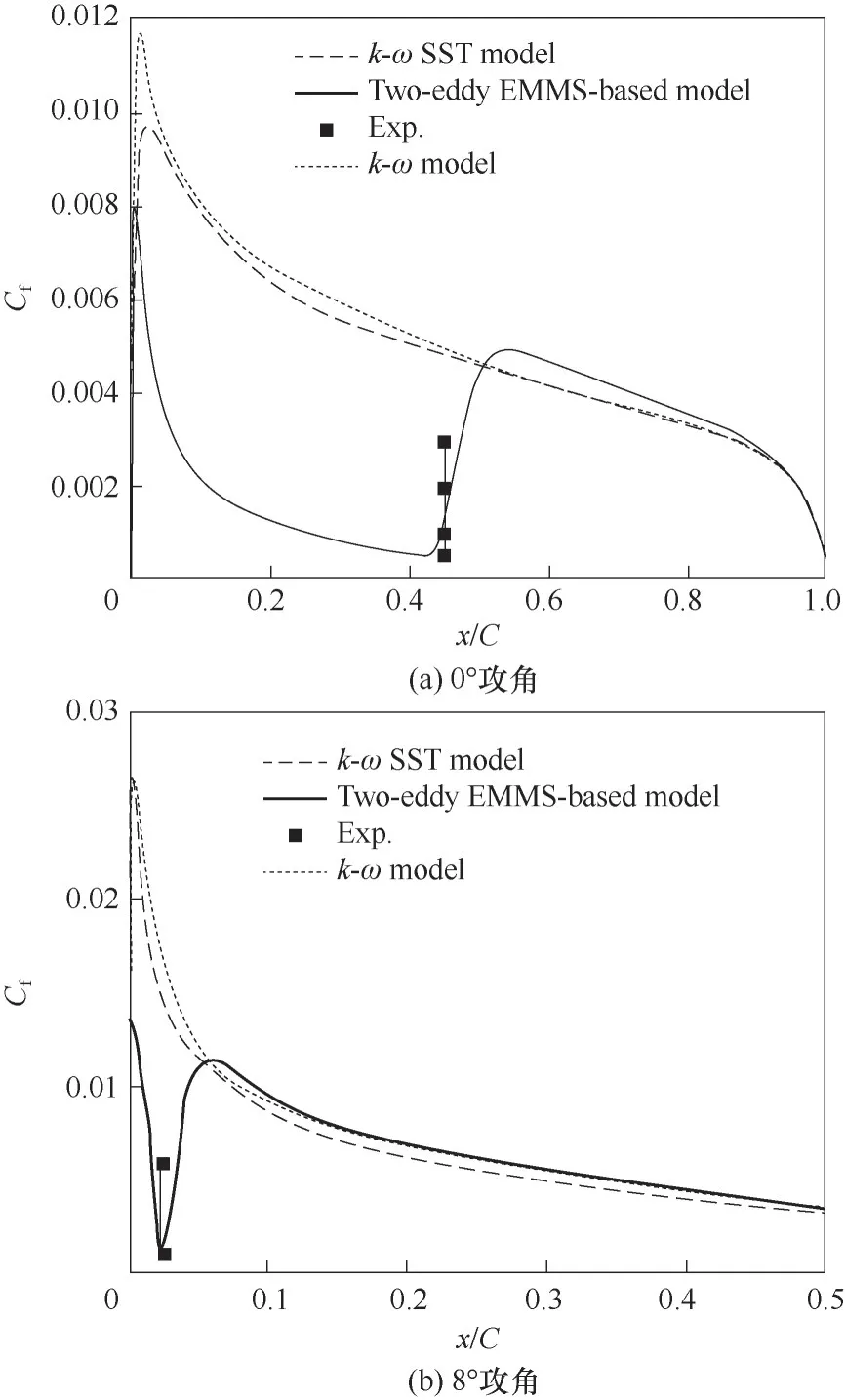
图10 双涡EMMS湍流模型和k-ω SST湍流模型预测NACA0012翼型表面摩擦系数Cf[55]Fig.10 Skin friction Cf predicted by two-eddy EMMS-based turbulence model and k-ω SST turbulence model in comparison with experimental data on the NACA0012 airfoil top-surface[55]

复杂的气候模型由描述大气、海洋、陆地表面和冰的数学方程组成[64]。气象大气和海洋模式涉及典型的工程湍流模拟，计算网格通常达到几十公里量级，在粗网格里湍动和非湍动（即层流）区域共存，而传统模式都是假设网格内是均匀状态，从而导致模型预测不准确。通过应用EMMS湍流模型对全球海洋环流进行了模拟，得到了初步结果（图11）。湍流结构只是网格内非均匀性的一部分，未来的工作可以将介尺度理论内涵扩展到更一般的情况，如计算网格内除了湍流，还可以考虑云、植被生长、雨雪、地形高程等在粗网格内的不均匀分布等，这些都属于介尺度理论的研究范畴。基于介科学概念考虑计算网格内的非均匀性，避免平均化方法的均匀处理，将会对天气预报和气候模拟的计算精度有很大改进。

图11 全球海洋环流的EMMS模拟Fig.11 EMMS modeling in ocean currents

3.4 EMMS湍流模型验证了介科学理论的普适性

介科学认为系统的复杂性源于共存的两种（或更多）主导机制之间竞争中协调[65]。不同机制的相对主导作用随着系统状态的变化而变化。以两种主导机制为例，系统将出现三个区域，即机制A 主导、机制A 和机制B 之间竞争中协调以及机制B 主导[66]。复杂性出现于机制A 和机制B 协调（共存）的介区域中。当系统状态处于两个极端区域之间的介区域时，不同共存主导机制之间竞争中协调导致了介尺度的复杂性[67]。因此，介科学很好地阐述了这种复杂性，对介尺度和介区域而言具有重要意义。

基于双涡EMMS 湍流模型同样计算出了Li等[40,66-67]提出的复杂系统中不同区域的行为。如图12 所示，随着流速的增加，依次出现了完全黏性控制、黏性和惯性之间竞争中协调以及完全惯性控制三种区域，大涡等效直径dL在中间位置出现了剧烈波动。说明流动的复杂性同样出现在黏性控制机制与惯性控制机制竞争中协调（层流成分和湍流成分流体共存）的介区域。这表明，介科学的概念在湍流系统中得到进一步证实，同时也为介科学理论作为复杂系统普适理论提供证据。

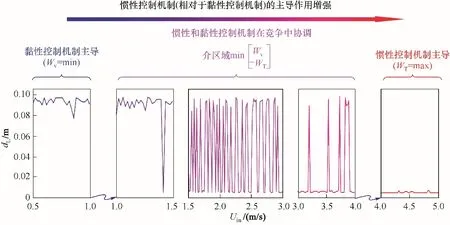
图12 湍流系统的三种区域预测Fig.12 Three-regime prediction identified in turbulence system

4 结论与展望

介科学聚焦于单元尺度和系统尺度之间存在的控制机制之间的竞争中协调导致的结构，并建立其稳定性条件，从而实现对介尺度结构及其性能的定量描述[65]。在揭示竞争中协调的主导机制及其关系时，应特别注意介尺度问题的层次特征，主导机制之间的竞争中协调导致了不同尺度上的结构差异和时空多尺度行为，每种主导机制自身的规律及其极值趋势。

湍流一直被认为是经典物理中最复杂的问题之一。一个多世纪以来，吸引了众多科学家的持续努力，但人们对它的认识还只是局部的，目前还没有完全令人满意的湍流理论。而在湍流模拟中，湍流模型对于模拟结果的准确性至关重要，而当前湍流模型大都是基于实验数据或经验关联式封闭湍流, 对物理模型的内部机理缺乏进一步探索，因而难以找到一种普适的湍流模型。介尺度湍流模型的发展将新兴的介科学思想与CFD 相结合，对模拟过程工程中的湍流问题和介尺度结构具有理论和实际意义。EMMS 建模思路成功地推广到湍流系统，通过建立工程湍流非均匀结构的物理模型，阐明其控制机制及其相互关系，解释了介尺度行为——非均匀涡团结构的形成机制及其对动量传递过程的影响。目前基于介科学视角下的EMMS湍流模型主要有如下进展：（1）在顶盖方腔流中捕捉到标准的k-ε模型无法预测到的三次角涡，与DNS结果更加符合；（2）基于双涡EMMS 湍流模型成功预测了平板及NACA0012 边界层转捩；（3）湍流系统中成功复现了介科学理论预测的完全黏性控制、黏性和惯性之间竞争中协调以及完全惯性控制三种区域，进一步验证了介科学理论在复杂系统中的普适性。

介科学有助于解决非均匀湍流系统的定量模拟，EMMS原理改进了湍流建模和模拟的精度，使其能够解决工程实际问题。湍流系统的EMMS模型为介科学作为共性原理提供了证据。EMMS原理对介尺度问题具有普遍性，EMMS 思路框架有助于交叉学科的融合发展，介科学的发展将极大提高不同学科解决复杂问题的能力。

致谢：感谢中国科学院过程工程研究所李静海院士长期以来对本研究给予的指导及鼓励！