浅埋地下建筑围护结构传热过程模拟研究

刘妙坤，崔萍，谢晓娜

(山东建筑大学热能工程学院，山东济南 250101)

0 引言

与地上建筑相比，地下建筑由于与土壤直接接触而具有特殊的传热特性，其研究更侧重楼地、墙壁和屋顶受土壤热物性因素影响下的传热问题[1-3]。根据文献[4]可知，距地表面15 m 处的地温波幅可以忽略不计，可将这一深度的地温看作地面年平均温度。 据此，将埋深＜15m 的地下建筑称为浅埋地下建筑，而埋深＞15m 的称为深埋地下建筑。

对于浅埋地下建筑，由于受地表温度场波动的影响，其热湿传递过程与深埋建筑相比更加复杂。当前，浅埋地下建筑冷热设计负荷的计算方法主要以一维传热为主，热负荷计算时主要采用简化的划分地带法，把地面沿外墙平行的方向分成4 个计算地带，同时忽略了传热系数的动态变化，通常取平均传热系数进行简易计算[5]；对于冷负荷的计算，多采用便于手写计算的冷负荷系数法，将地面传热视为有利因素，不考虑其带来的影响。 对于地下人防建筑的计算，GB 50038—2005《人民防空地下室设计规范》[6]中也仅对其围护结构的传热量给出简单的计算公式，将地下建筑传热过程视为简单的一维传热问题，未考虑传热系数的变化以及实际土层的蓄热作用。

目前，对于浅埋地下建筑的传热模拟方法，主要有解析解和数值解两种模型。 国内常应用数值解模型进行研究，运用有限元分析软件ANSYS、高级数值仿真软件COMSOL Multiphysics 等计算，此外还可以通过有限差分法编写数值程序求解[7-8]。 解析解法在国外的研究中应用较多，通过使用动态解析解法、分区温度区线估计法 (Interzone Temperature Profile Estimation，ITPE)等给出传热过程的二维或三维近似解[9-10]。 这些研究多采用简化计算方法，将室外温度直接视为非稳态正弦波动。 而实际中室外地表温度波动幅度大，将室外温度直接视为非稳态正弦波动将会忽略实际地表温度波动部分产生的热影响，同样会给计算结果带来较大误差。

针对上述的问题和不足，文章改进了地下传热计算方法，将室外温度取实际室外逐时地表温度。采用有限差分法编写数值程序建立地下建筑围护三维动态传热模型，在室外温度取实际室外逐时地表温度时，分析地下建筑热流及温度场变化情况；讨论了当前规范和文献中的常用简化计算方法，分析了各简化计算方法的不足，进而明确使用改进方法进行地下建筑传热计算的可行性。

1 浅埋地下建筑围护结构模型建立

1.1 围护结构物理模型

研究对象为一座浅埋地下建筑，物理模型如图1 所示，其中y 为研究区域水平方向长边距离，m；z为研究区域垂直方向距离，m；a 为地下建筑水平方向长边距离，m；h 为地下建筑垂直方向距离，m。 围护结构一般由多层材料构成，如区域Ⅰ、Ⅱ所示；围护结构外表面与土层紧密接触，因此周围土层与围护结构之间也存在传热过程，图1 中区域Ⅲ表示影响围护结构传热的土层区域。

图1 物理模型示意图

1.2 数学模型建立

地下建筑围护结构传热过程是一个三维非稳态无内热源周期性边界条件的导热过程，3 个区域的导热微分方程[2]可以由式(1)～(3)表示为

式中 ρ1、ρ2、ρ3分别为区域Ⅰ、Ⅱ、Ⅲ 的密度，kg/m3；c1、c2、c3分别为区域Ⅰ、Ⅱ、Ⅲ的比热容，J/(kg·K)；λ1、λ2、λ3分别为区域Ⅰ、Ⅱ、Ⅲ的导热系数，W/(m·K)；τ为时间变量，s；t 为 τ 时刻土壤温度值，℃；x 为研究区域水平方向短边距离，m。

1.3 边界条件设置

1.3.1 室外边界条件

浅埋地下建筑受室外气象参数条件变化影响较大，其室外边界条件较为复杂。 地下建筑的室外边界条件主要包括4 个绝热边界、室外地表面和土壤深处恒温边界。

将地下建筑底部向下 ＜15 m 视为恒温层，其温度约等于当地地表年平均温度[11]，由式(4) 表示为

式中tg，m为当地室外地表面年平均温度，℃；H 为恒温层深度，m。

地下建筑四周为无热量通过的绝热面，热流为0，其边界条件为第二类边界条件，可由式(5)和(6)表示为

式中λ 为土层导热系数，W/(m·K)。

1.3.2 室内边界条件

不考虑室内温度的波动，并忽略建筑内部产热，室内壁面边界条件由式(7) 和(8) 表示为

式中b 为室内壁面边界面距离，m；h 为内表面对流换热系数，W/(m2·K)；tf为室内空气温度，℃。

1.3.3 初始条件

根据文献[11] 中给出的公式，地层原始温度计算公式由式(9) 表示为

式中 t(x，y，z)为地层原始温度，℃；th为地层某一深度在某一时刻的原始温度，℃；Ag为地层表面温度波幅，℃；a 为地层材质的导温系数，m2/h；T 为温度波的波动周期，h。

2 围护结构传热过程计算程序设计

文章主要研究浅埋地下建筑围护结构温度与热流分布。 三维非稳态不稳定边界元程序设计流程图如图2 所示。 主要分为7 个步骤，下面将详细叙述网格划分、方程离散和室外地表边界条件取值等3个关键步骤。

图2 程序设计流程图

2.1 网格划分

将浅埋地下建筑整个传热区域沿径向及深度方向划分为若干个网格。 网格划分时，采用变步长的不均匀网格划分方法，在温度变化剧烈的建筑内部与外部交界位置采用小网格，向外逐渐增大。 x0、y0分别为横向和竖向起始网格距离，最小网格单元x0＝y0＝0.05 m，相邻网格间距差值增幅 Δσ ＝0.05 m；在深度方向上则均匀划分为70 个网格节点。 建筑x、y 方向向外延伸和z 方向向下延伸的距离均为15 m。 网格划分示意图如图3 所示。

图3 地下区域网格划分示意图

2.2 传热方程离散

应用有限差分法，对式(1)～(3)在时间和空间上都进行离散[12]。 节点示意图如图4 所示。

图4 节点示意图

离散得到的中心节点数值离散方程由式(10)表示为

式中 ΔV 为网格体积，m3；ρ 为土层密度，kg/m3；c 为土层比热容，J/(kg·K)；i、j、k 为 x、y、z 方向节点；Cx、Cy、Cz分别为 x、y、z 方向上的网格长度，m。

边界节点数值离散方程由式(11)表示为

2.3 室外地表面边界条件取值

谢晓娜[13]对地表温度进行傅立叶分解，分解为多个正弦波叠加的形式，将不同周期下各个正弦波的振幅列出，发现1 年周期的振幅明显高于其他周期。 因此，可将地表温度简化，由式(12)表示为

式中tg为室外地表温度，℃；Ak为室外地表温度经傅立叶分解后第k 阶正弦波的振幅；Pk为室外地表温度经傅立叶分解后第k 阶正弦波的相位；ak为室外地表温度经傅立叶分解后第k 阶正弦波的周期。

3 模拟计算结果分析

建筑围护结构具有对热作用的抵挡或利用的作用，从而使室内人员获得热舒适感。 1 d 之内室外气温与太阳辐射呈周期性变化，建筑围护结构受周期性不稳定热流波的作用[14]。 对于地下建筑而言，虽不受太阳辐射影响，但室外气温的波动同样会对其产生影响，且不同围护结构(如天花板、地面和四周墙壁等)的传热情况并不相同。 天花板由于与土壤不直接接触，其热流变化并不受土壤影响，故文章中涉及的水平围护结构只考虑地板的传热。 模拟计算中，将地下建筑四周的土层视为相同厚度，则建筑四周尺寸相同的垂直墙体，其热传递情况可以视为相同，故只在x、y 方向上各选取一面墙体研究其热传递问题。

针对室外温度存在逐时波动的特点，提出在计算时可将室外温度取实际室外逐时地表温度的方法。 以济南市某地下建筑为例，对其围护结构在不同室外温度下传热过程进行数值模拟，进而验证该种方法的可行性。 由建筑环境及暖通空调系统模拟软件DeST 可知，济南市室外地表面年平均温度为16.5 ℃，夏季温度取正号、冬季取负号。 该建筑长、宽、高分别为12.0、9.0、4.0 m，房间内表面对流换热系数为8.7 W/(m2·K)。 建筑周围土层为轻粘土，围护结构采用混凝土结构，由20 mm 厚水泥砂浆和40 mm厚碎石材料组成。 各材料热物性参数见表1。

表1 各材料热物性参数表

3.1 实际室外地表温度下地下建筑传热过程分析

实际情况中，热流波通过建筑围护结构到达室内表面的过程中，由于受到围护结构热容和热阻的作用，其波幅出现衰减和相位延迟现象，围护结构对室外气候具有一定的调节作用。 规定热流由室外流向室内为正，当热流密度为正时，内外表面温差较小，热流密度同样较小；当热流密度为负时，内外表面温差较大，热流密度同样较大，冬季则相反。 将室内温度设为23 ℃，室外温度设为济南实际室外逐时地表温度，得到围护结构1 年周期水平围护结构和垂直围护结构平均热流曲线，并与典型年室外逐时地表温度进行对比，结果如图5 所示。

图5 中黑色折线为实际地温下地下建筑水平围护热流曲线，可以看出1 年内变化幅度很小且为负值，表明全年内热流方向均为由地下建筑围护结构向土壤中传递；红色折线为实际地温下地下建筑垂直围护热流曲线，蓝色折线为济南实际室外逐时地表温度曲线，二者变化趋势相似，均为不光滑的正弦波动。 6～9 月垂直围护热流为正值且大于水平围护热流，表明此时间段内地下建筑主要吸收土壤传递来的热量。

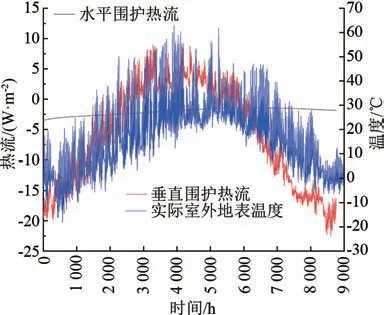
图5 实际室外地温下热流变化与典型年室外地表温度对比图

同时还可以看到，典型年室外逐时地表温度最大值约出现在3 750 h，而热流的最大值则约出现在4 300 h，二者间存在近1 个月的时间差，相位存在约6.28%的延迟，这是由于热量在自围护结构向土壤中传递时出现了延迟。 且垂直围护热流的变化整体虽为正弦波动，但每一时刻均伴随着细小波动，也体现了土壤的蓄热性，地下建筑的温度波在传递过程中出现了衰减。

土壤埋深对地下建筑传热过程也存在一定影响[15-17]。 为进一步研究实际地温工况下不同土壤埋深地下建筑围护结构热流变化情况，取该地下建筑长、短边两不同垂直围护结构作为研究对象，在其上沿z 方向自地表向下均匀取6 个点，深度分别为0.67、1.33、2.00、2.67、3.33、4.00 m，得到两垂直围护结构上各点1 年周期热流变化曲线，如图6 所示。

图6 两垂直围护结构上不同深度处实际热流图

由图6 可知，两垂直围护上相同深度各点处实际热流曲线基本一致。 深度为 0.67、1.33、2.00 m 处热流曲线呈现与图5 中1 年周期平均热流相似的不规则正弦波动形态，且振幅随深度增加而逐渐减小；深度为2.67、3.33、4.00 m 处热流曲线则变为光滑的正弦波动，振幅逐渐趋于平稳。 由此表明，地下建筑周围土壤厚度越小，热流曲线波动幅度越大；土壤厚度越大，热流曲线波动幅度越小。 这是由于深度越接近恒温层，地下建筑受地表温度影响逐渐减小，计算结果逐渐趋于稳定。 但同时也可以明显看出，应用实际室外地表温度作为室外温度进行传热计算时，若地下建筑周围土层厚度过小，则热流计算结果会出现较大误差，故土壤厚度的选择也是计算时需要考虑的一个重要因素。

除通过地下建筑围护结构的热流外，地下建筑内部温度场同样可以反映其热传递情况。 应用可视化后处理软件Tecplot 可得到该地下建筑连同周围土体在x ＝20 m 处截面冬、夏季温度场等温线，结果如图7 所示。

由图7 可以看出，冬季地下建筑相当于一个热源，向周围土层进行传热；等温线温度在0 ～23 ℃范围内变化，等温线在建筑周围分布密集，表明土壤主要与地下建筑进行热交换；0 ～17 ℃区间内等温线分布均匀，17 ℃后则为闭合曲线。 夏季热量由土层向建筑内传递，等温线在地表附近分布密集且基本保持平行，表明土壤主要与地表面进行热交换，与地下建筑几乎不发生热传递。

图7 实际室外地温地下温度场冬、夏季等温线图

观察等温线温度变化规律可见，冬、夏季土层温度均随土层深度增加而降低，在地下建筑下方土层深处趋于16.5 ℃后不再变化，表现出三维传热的特点，同时也符合设定恒温层为济南市室外地表面年平均温度16.5 ℃的条件。 同时，冬季地下建筑正下方区域温度略高于两侧环状区域，验证了远场边界线与建筑内墙的距离满足边界条件要求[18]，进而表明室外温度取实际室外逐时地表温度时所得地下建筑传热过程符合非稳态传热特性。

由上述分析可知，实际情况中地下围护热流变化是一个受到诸多因素影响的复杂变化过程。 为分析当前常用的地下建筑传热计算方法存在的不足，下面将以地下建筑围护结构1 年周期平均热流值计算为例，对规范中给出的热流计算公式、当前研究中常用的非稳态工况和室外温度简化为稳态与1 年周期正弦波叠加工况下地下建筑热流计算方法进行分析讨论。

3.2 常用地下建筑传热计算方法讨论

3.2.1 稳态计算方法

GB 50038—2005[6]中对地下建筑围护结构传热量给出计算公式，由式(13)表示为

式中Q 为围护结构的散热量，W；k 为围护结构的平均传热系数，W/(m2·K)；F 为外墙及底板内表面面积，m2；tn为室内设计计算温度，℃；t0为土壤初始温度，℃。

根据土壤导热系数λ 取值不同，围护结构平均传热系数k 可使用线性内插法取值，规范中给出了部分参考数值有 λ ＝ 0. 92 W/(m ·℃)、 k ＝0.71 W/(m2·℃)； λ ＝ 1. 16 W/(m ·℃)、 k ＝0.80 W/(m2·℃)； λ ＝ 1. 73 W/(m ·℃)、 k ＝1.06 W/(m2·℃)。

模拟过程中将土壤导热系数取 λ ＝1.0 W/(m·℃)，故相应围护结构平均传热系数k ＝0.74 W/(m2·℃)。 热流q 计算公式可由式(14)表示为

所得到的该地下建筑应用规范方法的计算结果为q ＝14.93 W/m2。 将该热流计算结果与实际室外地表温度下热流计算结果进行对比，结果如图8所示。

图8 GB 50038—2005 方法热流计算结果与实际室外地温热流结果对比图

由图8 可知，应用规范中的方法进行热流计算所得结果为不随时间变化的恒定值，与实际室外地温下垂直围护热流计算所得正弦波动相差较大，故规范中给出方法不适用于实际地下建筑复杂的三维传热过程。

3.2.2 非稳态计算方法

当前对于地下建筑的二维和三维非稳态传热问题，研究时多将室外温度看作简单正弦波动。 将室内温度设为23 ℃，室外温度设为1 年周期正弦波，所得水平和垂直围护结构1 年周期平均热流曲线如图9 所示。

由图9 可知，非稳态室外温度下热流曲线形态与实际地表温度下热流曲线相比仍存在明显差异。0～8 760 h 内水平围护热流在-31～-12 .5 W/m2范围内变化且持续上升，垂直围护热流曲线在-35 ～-15 W/m2范围内变化且为不完整的带有细小波动的正弦波动，最大值约出现在5 500 h，比实际工况下热流最大值出现时间4 300 h 推迟约1 200 h。 相位波动出现约13.70 %的延迟，相比实际室外温度最大值出现时间3 750 h 更是存在20.00%的误差，表明该种室外温度下热流值计算误差较大，即该种热流计算方法同样存在局限性。

图9 非稳态热流计算结果与实际地温热流结果对比图

3.2.3 稳态与非稳态叠加计算方法

由文献[11]可知，对地下建筑传热进行计算时，还可将室外温度分解为稳态＋1 年周期正弦波。将室内温度设为23 ℃，室外温度设为稳态15 ℃＋1 年周期正弦波，得到水平和垂直围护热流曲线。由于该曲线同样呈正弦波动，将其与实际地温下围护热流曲线进行对比，结果如图10 所示。

图10 稳态＋1 年周期正弦波热流曲线与实际热流曲线对比图

由图10 可知，稳态与非稳态叠加室外温度下，0～8 760 h内水平围护热流曲线形态和变化范围与实际情况下热流曲线相比基本相同，仅存在约为1 W/m2的差值；垂直围护热流为光滑的正弦波曲线，变化范围与实际工况下热流曲线基本相同，最大值约出现在4 700 h，比实际工况下热流最大值出现时间4 300 h 推迟约400 h。 相位波动出现约4.57%的延迟，相比实际室外温度最大值出现时间3 750 h存在10.84%的误差。 由此可见，虽然室外温度为稳态＋1 年周期正弦波时地下建筑围护水平热流计算结果与实际情况最为相似，但同样存在误差且不可忽略，表明该种计算方法同样存在不足。

4 结论

文章采用MATLAB 软件建立济南市某浅埋地下建筑传热的数值模型，分析当室内温度设定为恒定23 ℃时，室外温度取实际室外逐时地表温度和当前规范与文献中常用的3 种室外温度下，地下建筑传热计算结果。 得出的主要结论如下:

(1) 室外温度取实际室外逐时地表温度时，全年热流变化趋势与典型年室外地温变化趋势相似。由于土壤存在蓄热特性，1 年内热流最大值较最高温出现时间存在1 个月的延迟，误差约为6.28%；垂直围护结构上不同埋深处热流随土壤深度变化呈现深度越小波动越大的趋势，温度场变化符合三维非稳态传热规律，证明该种计算方法适用于地下建筑三维非稳态传热问题。

(2) 使用规范中的稳态方法进行计算时，围护热流为无波动的恒定值；使用非稳态室外温度进行计算时，热流曲线相位波动较(1)中方法延迟约13.70%，与实际温度间误差约为20.00%；使用稳态＋1 年周期正弦波作为室外温度进行计算时，热流曲线相位波动较(1)中方法延迟约4.57%，与实际温度间误差约为10.84%。 所以3 种常见简化方法计算地下建筑围护热流值均与实际情况间存在较大误差，文章提出的计算方法具有更高的准确性。