花江北盘江大桥六枝岸高陡边坡稳定性评价①
2022-07-06李军伟胡弘毅梅松华任虎程贺建清
李军伟, 胡弘毅, 梅松华, 任虎程, 贺建清
(1.湖南省自然资源调查所,湖南 长沙 410014;2.湖南科技大学,湖南 湘潭 411201;3.中国电建集团中南勘测设计研究院有限公司,湖南 长沙 410014)
拟建的花江北盘江大桥是贵州省六枝至安龙高速公路跨越北盘江大峡谷的一座特大桥梁,系六枝至安龙高速公路的控制性工程。 桥址区位于贵州省关岭县花江镇科力寨村至贞丰县花江村,地形为深切河谷,受北盘江冲刷侵蚀,河谷呈“V”字型,两岸呈陡坎地形;可见一级河流阶地,属于中切峰丛峡谷地貌。 由于拟建大桥地处高山峡谷,两岸地形变化剧烈,起伏大,桥位岸坡的整体稳定性对保证大桥顺利建设和长期安全运营有着决定性影响[1]。 根据大桥初步设计,在桥位(K 线)选择主跨1 366 m 钢桁梁悬索桥方案为初步设计方案[2]。
如何在稳定性分析中反映大桥岸坡的岩体结构特征以及变形破坏模式,是准确判断岸坡稳定与否的关键[3]。 本文根据地勘成果,利用工程类比和经验方法初步确定边坡岩土体物理力学参数,针对推荐方案,建立北盘江大桥六枝岸(北岸)边坡地质概化模型,采用极限平衡分析法和基于强度折减原理的三维有限差分FLAC3D软件,对花江北盘江大桥六枝岸(北岸)边坡进行整体稳定性计算分析,综合评价自然边坡和工程边坡的稳定性,为大桥初步设计方案论证提供科学依据。
1 边坡工程地质分析
花江北盘江大桥六枝岸地层岩性为三叠系中统杨柳井组(T2y)厚层、中厚层状白云岩[2]。 近北盘江岩层产状为30°~36°∠30°~35°,岩层倾向与桥轴线呈79°相交且岩层倾向与坡向相反(见图1),为反倾向层状结构边坡,岩层产状有利于边坡的整体稳定。 虽然局部受风化裂隙、节理影响发生崩塌现象,但规模一般小于5 m3。 边坡中上部岩层产状为195°~220°∠45°~66°,岩层产状呈上缓下陡的形态分布,岩层倾向与桥轴线呈63°~73°相交,为中倾-陡倾顺层边坡。 其中索塔位置岩层为210°∠66°。
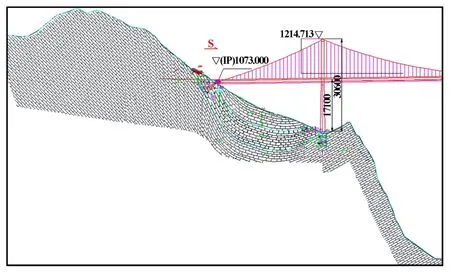
图1 六枝岸桥轴线边坡工程地质纵剖面
六枝岸边坡中上部自然边坡坡角小于岩层倾角,有利于边坡稳定;边坡下部为一反倾层状构造的陡崖,相当于给中上部中倾-陡倾顺层边坡压脚,边坡整体稳定性好,不会发生整体顺层滑动破坏。 因下伏基岩为中厚层中风化三叠系中统杨柳井组(T2y)白云岩、灰岩,也不会发生滑移-弯曲破坏型(溃曲)破坏。
六枝岸垂直于桥轴线边坡,岩层倾向与桥轴线垂直线呈79°夹角,岩层倾角11°,边坡自然坡度9°~18°,为典型的层状正交边坡,整体稳定性较好。边坡表面覆盖层厚度3~10 m,有可能因施工扰动出现覆盖层沿基岩面或沿弧形滑裂面的局部破坏。
六枝岸边坡节理主要有J1(25°∠8°)和J2(110°∠78°)两组。 J1 节理间距0.15 ~0.4 m,平直、微张、延伸大于1.5 m;J2 节理间距0.2 ~0.4 m,平直、微张、延伸大于2.0 m。
基岩未见有明显切脚,其周围亦无规模较大的边坡变形破坏,边坡处于稳定状态,但溶沟、溶槽、石牙等溶蚀现象发育。
六枝岸边坡可能的变形破坏模式为:由于岩体节理、层面、各种裂隙切割形成的楔形体滑移和局部块体掉块、崩塌以及覆盖层沿基岩面或沿弧形滑裂面的局部破坏。
2 边坡稳定性安全系数选取标准及岩土体力学参数选取
2.1 边坡稳定性安全系数选取标准
目前,我国与特大型桥梁建设有关的边坡工程还没有相关设计规范,在桥梁边坡设计与校核过程中,边坡允许安全系数的取值问题一直是设计人员十分关心而目前尚未彻底解决的问题。 为此,专门收集、研究了国内相关行业边坡工程设计规范[3-7]中关于边坡安全系数标准规定以及国内有影响的重大水电工程、桥梁工程边坡安全系数取值情况,来确定花江北盘江大桥边坡的安全系数选取标准。 综合考虑花江北盘江大桥桥位区的工程地质条件、工程重要性等级等因素,将其边坡安全系数设计标准初步拟定为:正常工况(自然状态、岩体自重+桥梁荷载)条件下取1.35,地震工况条件下取1.10,暴雨工况条件下取1.20。
2.2 边坡岩土体力学参数选取
在北盘江大桥六枝岸(北岸)边坡的稳定性分析中,除了按传统的工程地质综合评价方法确定强度指标外,还采用Hoek-Brown 建议的经验公式[8-11],结合相关边坡工程的经验,确定了节理岩体强度推荐范围值,如表1 所示。
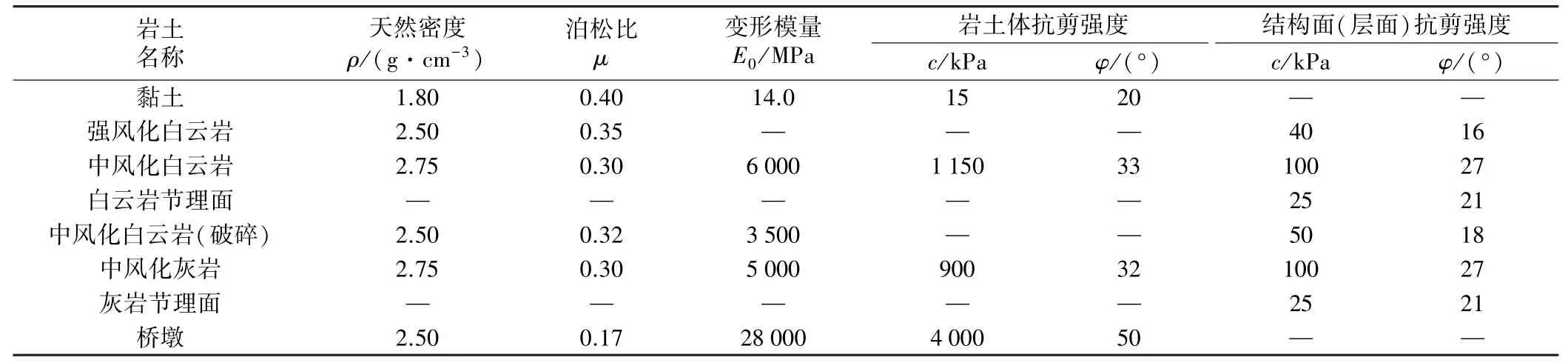
表1 花江北盘江大桥边坡岩土体及桥墩材料物理力学参数推荐值
3 边坡稳定性分析
本次边坡稳定性计算分析采用Slide.v6007 以及FLAC3D6.0 对桥址区边坡分别进行二维极限平衡分析和三维有限差分分析。
3.1 计算工况
计算工况见表2。 暴雨工况主要通过对岩土体强度参数折减的方式进行模拟,计算过程中强度参数折减系数取0.85。

表2 花江北盘江大桥六枝岸边坡稳定性计算工况表
二维极限平衡分析所取分析边坡为单位宽度,对承台底部荷载应按承台单位宽度所受荷载进行施加。因此在二维计算过程中,在对单宽剪力和单宽轴向压力合成后按照合力的方位施加于承台底。 三维计算过程中荷载(压力、剪力)以面力形式施加到桥梁索塔及锚碇基坑底面。 地震惯性力参照SL 386—2007《水利水电工程边坡设计规范》[12]附录D2 的有关规定计算。 岩体自重+桥梁荷载见表3。
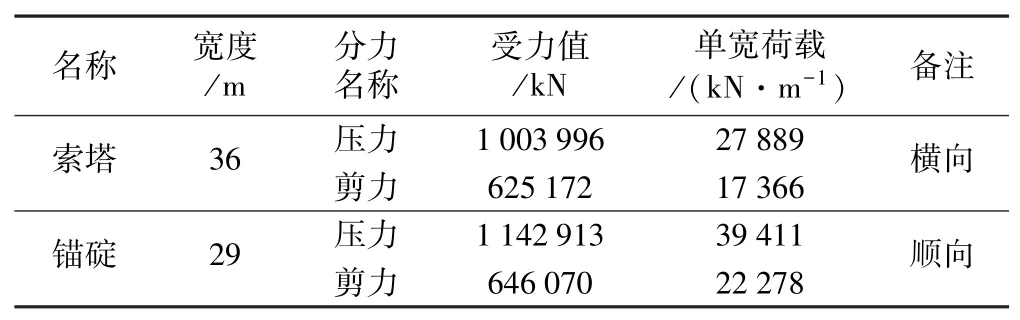
表3 六枝岸边坡稳定计算岩体自重+桥梁荷载表
3.2 边坡稳定性二维分析
3.2.1 二维地质概化模型
根据计算要求及工程地质条件,不同边坡潜在失稳模式不同,需根据工程地质条件进行概化,建立工程地质概化模型。 考虑到桥梁的主要水平荷载方向为顺桥轴向和垂直于桥轴线方向,在二维计算时,一般选择桥位桥轴线纵剖面边坡和主塔位置垂直于桥轴线横断面边坡来进行分析。 因主塔位置垂直于桥轴线横断面边坡整体稳定性较好,本文不做分析。 图2 为六枝岸桥轴线纵剖面边坡计算概化模型。
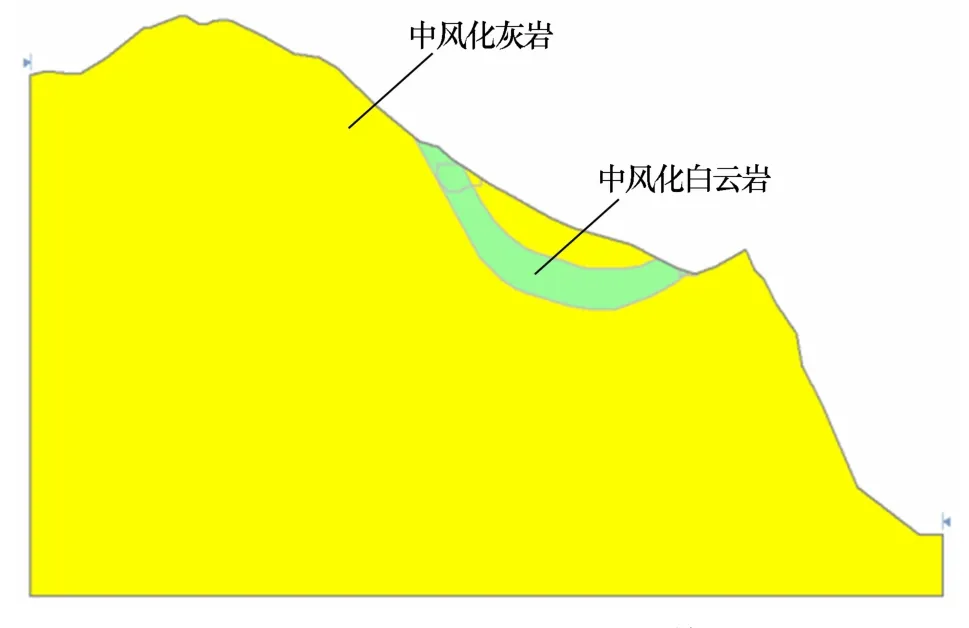
图2 六枝岸桥轴线纵剖面边坡计算概化模型
3.2.2 边坡稳定性极限平衡分析
对于沿圆弧滑动面破坏的边坡,极限平衡分析一般先采用滑裂面自动搜索,然后采用M-P 法、Bishop法和Janbu 法计算安全系数,取三者中的最低值为边坡计算安全系数。 对于沿层面或接触面破坏的边坡,在岩层接触面及岩层内设置数条滑裂面(一般按照滑裂面所处位置的深度设置表层、浅层以及深层等假定滑裂面),对每个滑裂面采用3 种计算方法计算安全系数,选择其中安全系数最低的滑裂面作为潜在滑裂面,再计算边坡安全系数,取三者中的最低值为边坡计算安全系数。 六枝岸桥轴线纵剖面边坡二维极限平衡法分析结果见表4。

表4 花江北盘江大桥六枝岸桥轴线纵剖面边坡稳定性极限平衡分析结果
3.3 边坡稳定性三维分析
3.3.1 三维地质概化模型
计算模型坐标系:平行桥轴线方向为Y轴(方位角47°),以朝安龙侧位Y轴为正向,垂直桥轴线为X轴,竖直方向为Z轴,向上为正。
六枝岸边坡三维计算范围(见图3):X轴方向(垂直桥轴线方向),以桥轴线为基准,向上下游方向各延伸300 m;Y轴方向(平行桥轴线方向),以索塔中心为原点,向北侧延伸700 m,向南侧延伸650 m;Z轴方向(竖直方向),从高程400 m 至地表。 计算模型采用四面体、五面体和六面体混合网格单元进行离散,共划分单元105 560 个,节点21 248 个,三维网格见图4。
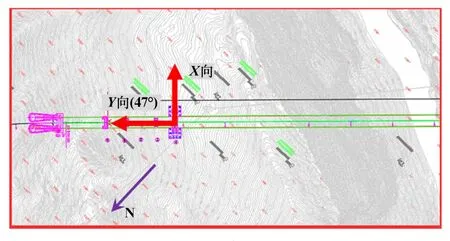
图3 边坡三维计算模型范围示意图
三维数值模型中,锚碇与索塔的位置如图5 所示。
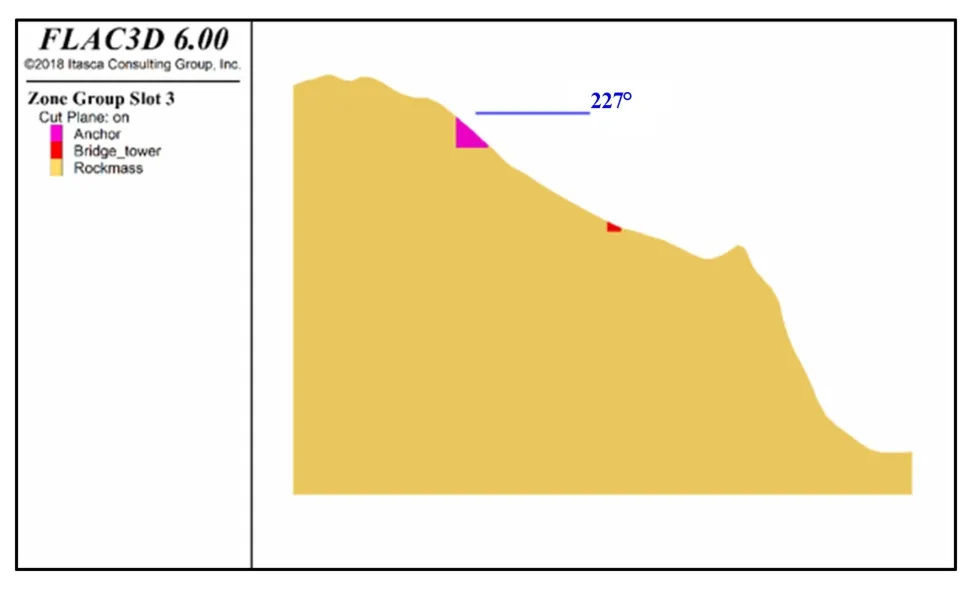
图5 边坡三维计算模型中锚碇与索塔的位置
在3 个相邻的边坡剖面布置监测点(见图6),监测各点在三维强度折减计算中的速度和位移,根据各监测点速度和位移的收敛情况,判断坡体的临界安全系数,即边坡稳定性安全系数。
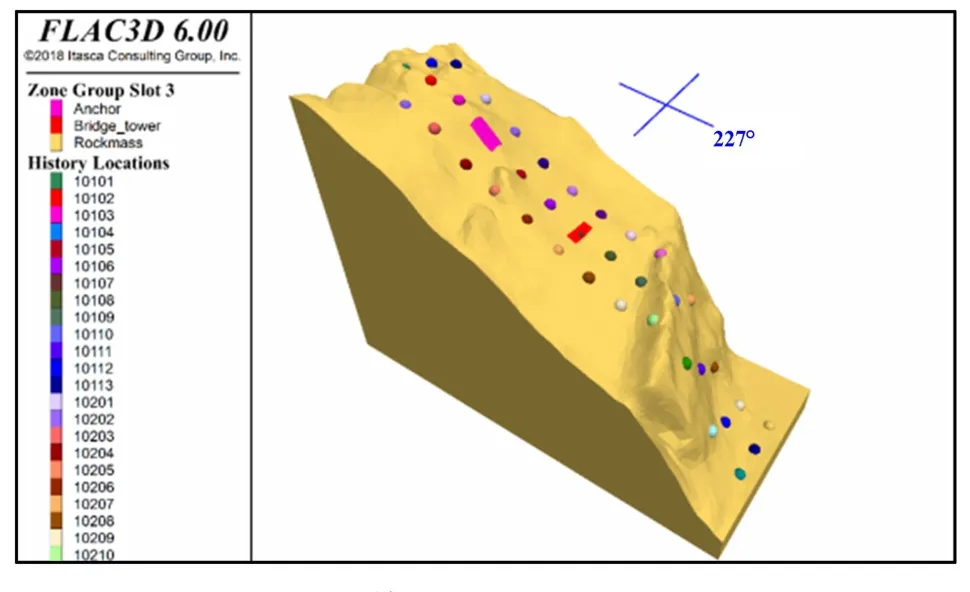
图6 三维计算模型中位移与速度监测点
3.3.2 边坡稳定性三维有限差分强度折减分析
工况3 条件下,边坡表面各监测点位移及速度变化特征的计算结果如图7 所示。 其纵坐标为位移及速度大小,横坐标为强度折减系数,不同曲线代表相应坡表不同位置的监测点。 不同部位变形响应的差异显示了各部位稳定性的不同。
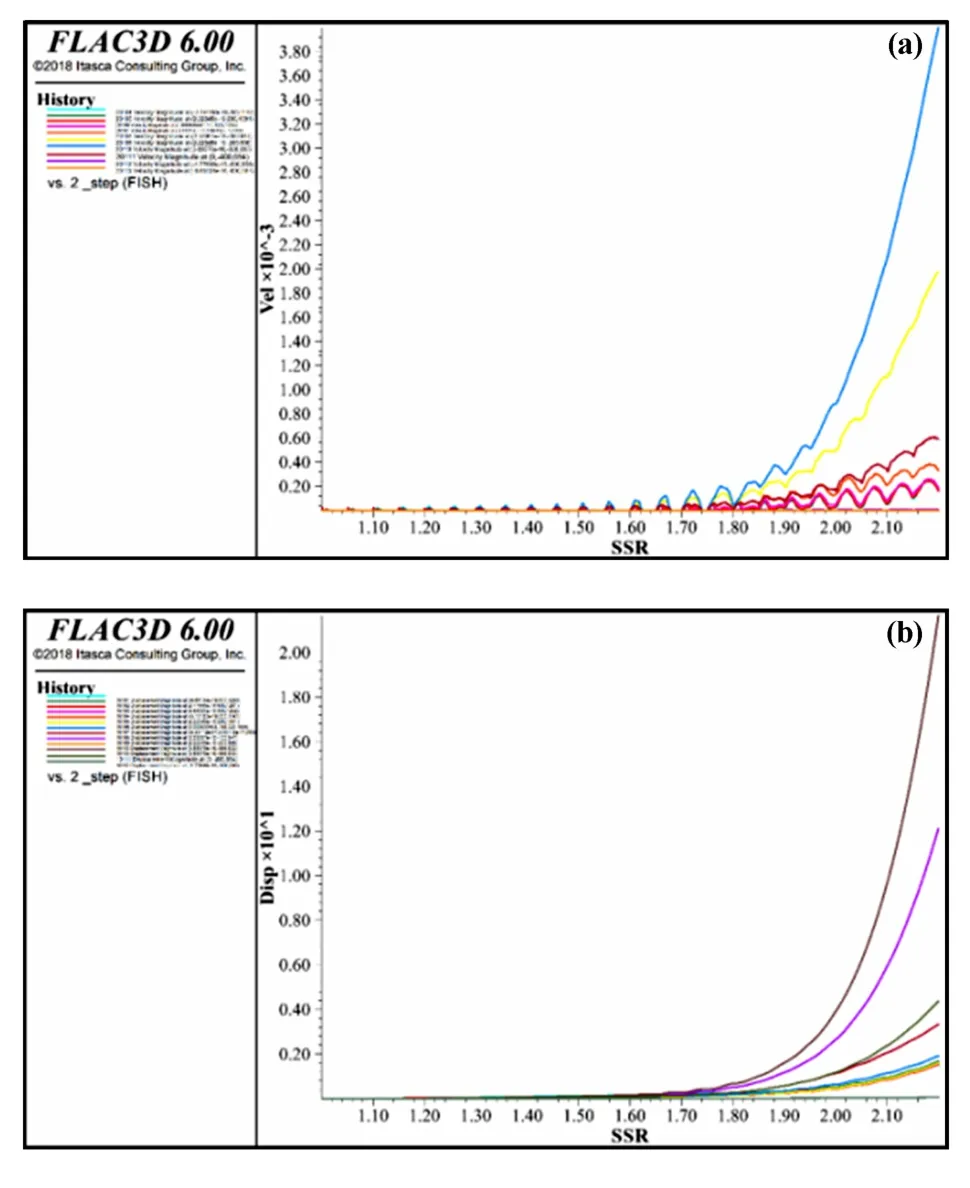
图7 边桥梁荷载作用下边坡数值监测结果与折减系数关系曲线(X=0 剖面)
从图7 可见,监测点的速度和位移分别在安全系数1.80 左右开始出现不收敛特征,监测点的速度和位移接近同时发散。 综合判定边坡在工况3 下安全系数为1.80。 其他工况条件下,安全系数的获取以此类推。
图8~10 以临界状态总位移和剪切应变的形式给出了边坡在失稳状态下的潜在滑面。 由图可见,边坡各剖面的失稳模式基本以近似圆弧型整体失稳,失稳模式与二维计算获取的结果一致。

图8 桥梁荷载作用下边坡潜在滑裂面示意图(X=0 剖面)
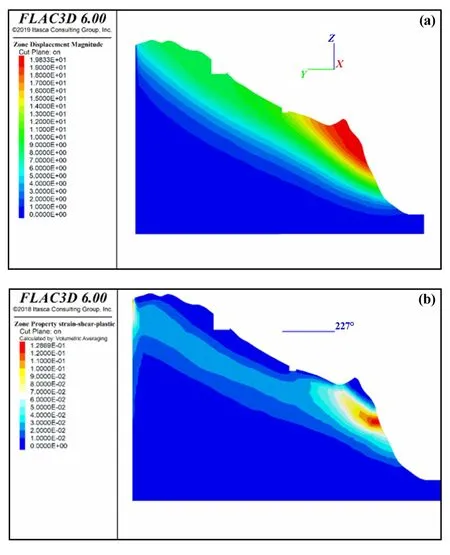
图9 桥梁荷载+地震作用下边坡潜在滑裂面示意图(X=0 剖面)
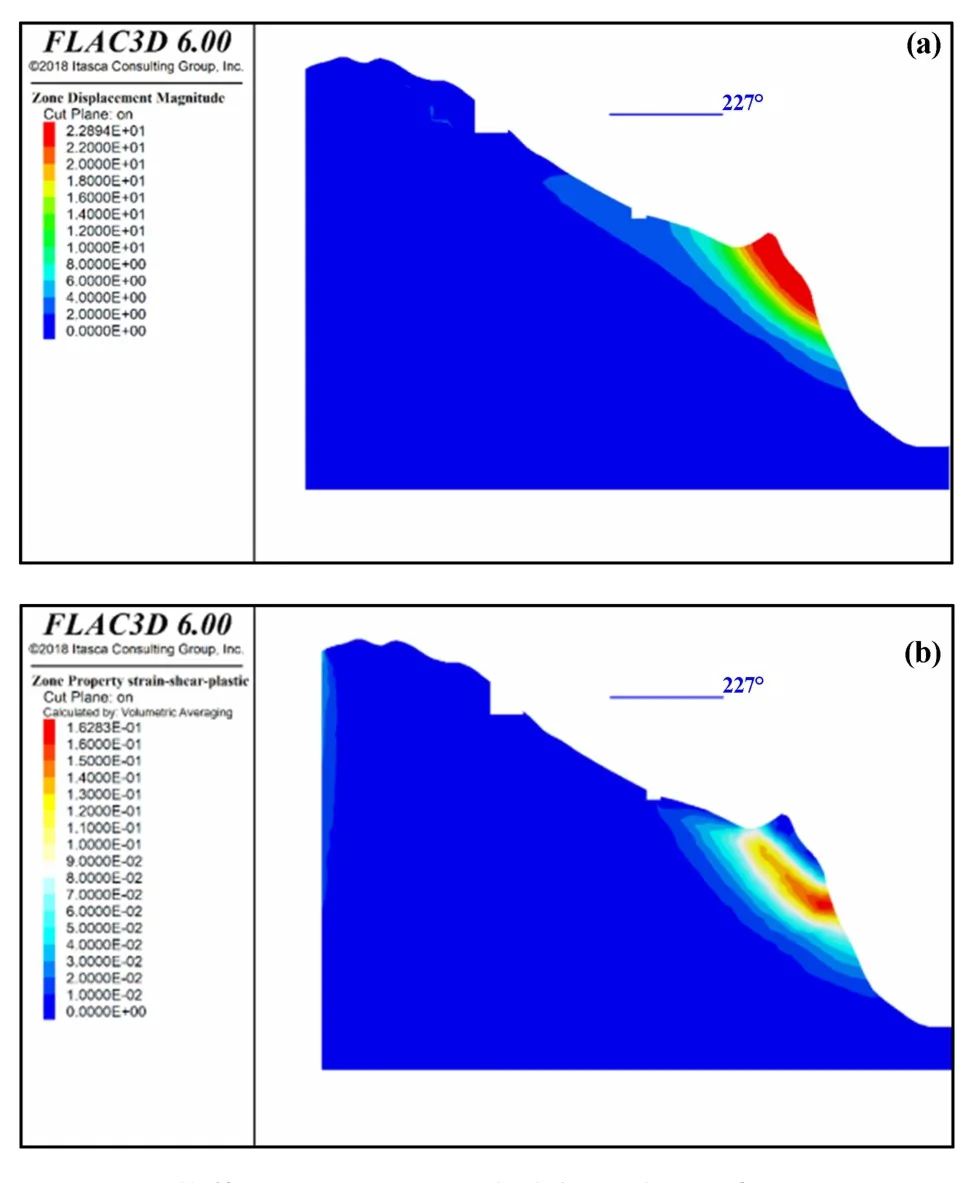
图10 桥梁荷载+暴雨作用下边坡潜在滑裂面示意图(X=0 剖面)
3.4 边坡稳定性计算结果
各工况条件下二维、三维稳定性计算结果对比见表5。 由表可以看出,二维、三维稳定性分析结果规律一致,均满足边坡稳定性设计要求,且有一定安全裕度。 相较于二维极限平衡法,三维有限差分强度折减法计算得到的安全系数略大,这是三维条件下边坡受三维方向的约束作用而导致其计算结果比极限平衡分析结果偏大,符合一般规律。
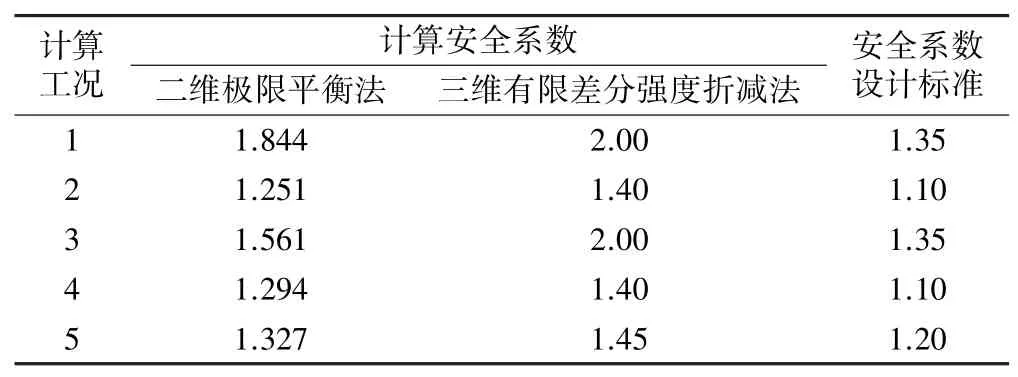
表5 花江北盘江大桥六枝岸边坡稳定性计算结果对比
4 结 论
系统研究了花江北盘江大桥推荐桥位六枝岸边坡工程地质特征,分析了边坡可能出现的变形破坏形式;根据地勘结果,利用工程类比和经验方法初步确定边坡岩土体物理力学参数;基于大桥初步设计桥型方案,采用极限平衡分析和三维有限差分方法(FLAC3D),分别评价了花江北盘江大桥六枝岸边坡的稳定性,得到如下主要结论:
1) 各工况条件下,二维、三维稳定性分析结果规律一致,均满足边坡稳定性设计要求,且有一定安全裕度;边坡各剖面的失稳模式基本以近似圆弧型整体失稳。
2) 相较于二维极限平衡法,三维有限差分强度折减法计算得到的安全系数略大。
