脉冲调制微波放电等离子体的数值模拟
2022-07-05刘壹顺秦绍华
刘 鹏,李 娜,陈 童,刘壹顺,杜 军,潘 杰,秦绍华
(山东师范大学物理与电子科学学院,山东 济南 250014)
微波放电是在微波激励源的激励之下,由波导或微波传输线传输能量,在微波谐振腔内形成非平衡放电等离子体的气体放电。相较于直流、低频、射频等其他激励方式,微波放电的频率较高,有助于提高放电时的电子密度,具有粒子密度高、放电均匀稳定、能量转化效率高和无电极污染等优点[1-2]。微波放电等离子体技术最早可以追溯自上世纪60年代,经过多年发展,已经成为一种成熟的等离子体发生技术,广泛应用于元素检测、薄膜沉积、表面清洗、辅助燃烧和温室气体处理等领域。
微波电源频率为GHz数量级,放电产生的活性粒子随电场振荡,并被限制在放电空间中。连续型放电产生的等离子体热效应积累严重、温度较高、功率消耗大,限制了其应用[3]。利用脉冲调制微波激励源间断性给电,避免了连续性放电的缺点。脉冲调制微波放电可以有效地抑制气体加热效应和降低能耗,同时保持较高的电子能量和电子密度,优化等离子体的产生。
微波谐振腔内微波放电作用可以用约化电场强度(E/N)等效表示,脉冲占空比决定了微波作用的时间。张鹏[4]、刘肖[5]等人在分析放电自由基产物时,发现产物组分的摩尔分数会随着约化电场强度的改变发生变化,当约化电场强度较低时,部分产物基本不能生成。Starikovskiy A等人指出约化电场强度会明显影响电子能量沉积方向和单个自由基产生的平均能量消耗值[6]。Annemie Bogaerts文章中提到,微波的约化电场强度会影响振动激发和电子激发的能量[7]。张远涛等人利用占空比和脉冲调制频率来优化峰值电流和高能电子的产生[8]。上述研究主要集中在氦气或者氦气加入少量的空气。本文主要针对约化电场强度和占空比对氩气和湿空气微波放电等离子体的影响进行了研究。
本文后续安排如下,第一节介绍等离子体动力学模型。第二节讨论不同约化电场强度和占空比下电子密度和温度的时间演化与平均粒子密度的变化,以及空气反应中粒子的主要生成路径。第三部分是总结。
1 等离子体动力学模型
本文建立零维氩气与湿空气微波放电等离子体模型,分别以氩气与湿空气作为背景气体进行仿真。各自的比例成分是N2:O2:H2O=78:21:1,密度初始值N2为1.9×1019cm-3,O2为0.5×1019cm-3,H2O为0.2×1018cm-3。Ar的为2.4×1019cm-3。参照Bogaerts论文中微波等离子体模拟的典型值,气体压力为2660 Pa、微波功率为400 W、微波频率为2.45 GHz、脉冲调制频率为1 KHz。数值模拟的约化电场强度中间值设为55 Td,脉冲占空比中间值为50%[9-10]。模型中的主要粒子如表1所示。初始离子、自由基密度分别设为107和105cm-3。

表1 模型中的粒子种类Tab.1 The pecies of particles in the model
本文微波放电等离子体模型的控制方程主要由零维连续性方程、电子能量方程组成[11]。本模型中,第i种粒子密度的时间演化Ni用连续方程表示:
(1)
其中,Ni是ith物种的粒子密度,Rij是第jth个反应对应的第ith种源速率。在反应边界处,由于器壁对粒子的吸附及碰撞导致的壁反应,会出现边界损失现象。本文中采用的零维模型对空间采取均匀化处理,未考虑边界损失现象。
电子能量密度方程用于求解电子温度,电子温度Te影响反应速率系数,用于在ZDPlaskin中求解粒子密度。电子能量密度方程[11]表示为:
(2)
式中,dε是电子能量密度。dε=(3/2)dekBTe,kB和Te分别是玻尔兹曼常数和电子温度,de是电子密度,J和E是放电电流密度和电场。εi和ki分别是第i次非弹性电子碰撞过程中的能量损失和反应速率系数,di是粒子经过第i次非弹性碰撞后的粒子密度,me、Mu分别为电子质量和粒子u的质量。vm是电子与粒子之间的动量交换碰撞频率,Tu为粒子u的温度。本模型中重粒子温度Tu等于气体温度Tg,设为300 K。重粒子反应后温度可能发生变化,更精确的模型应当包括重粒子温度平衡方程。
模型中考虑电子碰撞电离、电子碰撞激发、电子吸附反应、电子-离子反应、三体反应、中性-中性反应、电子碰撞电子激发、离子-自由基反应、电子-离子复合、电子-离子离解复合等反应类型。
微波放电过程中等离子体动力学数值模型的求解采用零维动力学求解器ZDPlaskin,其与求解电子玻尔兹曼方程的BOLSIG+数值求解器相耦合。BOLSIG+数值求解器通过读取具体反应的截面数据后,计算其反应速率系数,并将反应速率系数提供给ZDPlaskin求解器用来计算粒子密度[12]。部分反应速率系数可以通过文献直接获得,如附录所示。
2 计算结果与讨论
2.1 约化电场强度和占空比对电子密度时间演化的影响
首先本文将占空比固定为50%,在45~65 Td范围内调节约化电场强度,模拟空气与氩气微波放电电子密度的时间演化过程,仿真结果如图1所示。

图1 不同E/N下电子密度的时间演化(a)空气(b)氩气Fig.1 Time evolutions of electron density at different E/N(a) Air (b) Argon
图1(a)为不同E/N下的空气介质电子密度的时间演化。在放电阶段,空气的电子密度峰值随E/N的增加而逐步上升。当E/N为45 Td时,电子密度的变化比较平缓,超过45 Td,电子密度呈现快速增长的趋势。在余辉阶段,当E/N为45 Td时,电子密度下降缓慢,从45到55 Td,空气电子密度下降速率逐渐增大,从55到65 Td,电子密度下降速率变化不大。可见通过约化电场强度E/N可以调节电子密度,进而优化大气压下脉冲调制微波放电等离子体应用[13-14]。
图1(b)给出不同E/N下氩气电子密度的时间演化。放电阶段,随E/N数值的增加,氩气的电子密度峰值同样逐步增大,但上升和下降速率变化不大。对比图1(a)和图1(b)可见,在相同E/N下空气的电子密度峰值低于氩气。因为氩气是惰性气体,其电子更易被激发,电子密度的峰值较高且稳定。
将E/N固定为55 Td,占空比在10%~90%范围内进行调节,模拟空气与氩气微波放电电子密度的时间演化过程,仿真结果如图2所示。
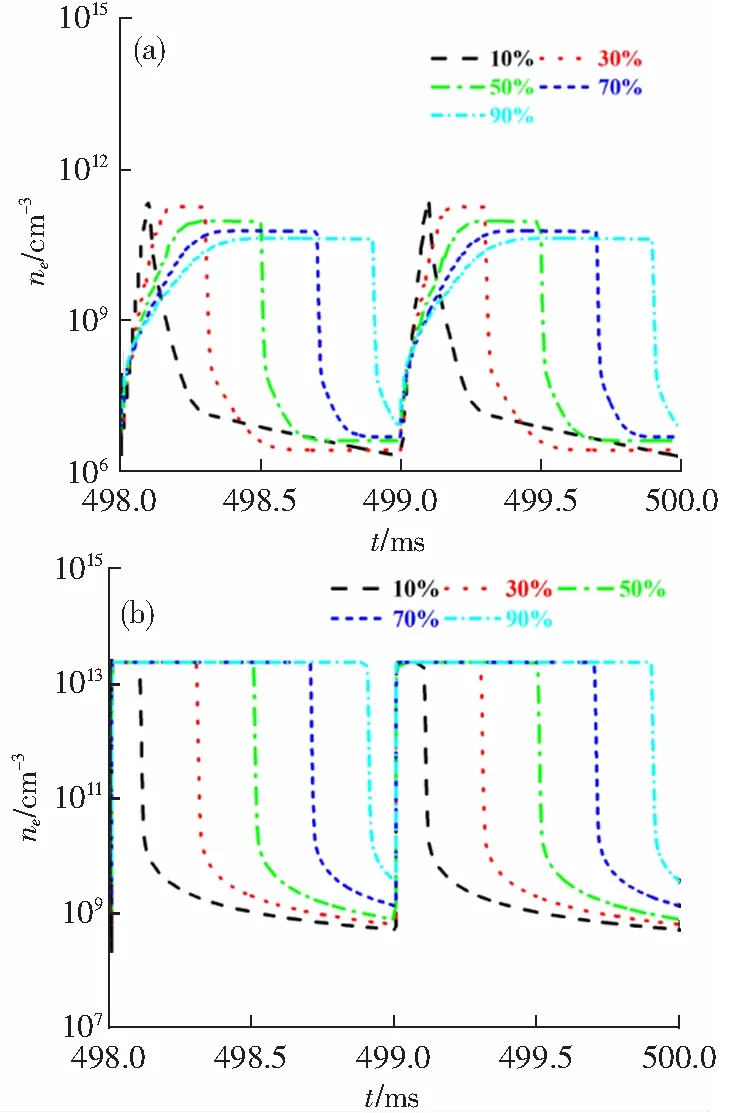
图2 不同占空比下电子密度的时间演化(a)空气(b)氩气Fig.2 Time evolutions of electron density at different duty cycles (a) Air (b) Argon
由图2(a)可见,随着占空比的增大,空气电子密度峰值逐渐下降,变化速率逐渐减缓,但峰值持续时间逐渐变长。占空比增加,微波放电持续时间增加,反应损耗的电子也随之增多,导致电子密度峰值的下降。在大气微波放电过程中,当占空比很小时,会形成一个非常强的反转电场来重新加热阴极鞘层中的电子,产生高能电子[14]。因此当占空比为10%,电子获得一个较快的激发,电子密度迅速达到峰值,随着占空比的继续增大,电子密度的变化率放缓,而脉冲放电时间的变长,会相应地导致电子密度峰值持续的时间的变长。
图2(b)给出不同占空比下氩气电子密度的时间演化,在不同的占空比下,氩气的电子密度峰值相同,放电持续时间跟占空比呈正相关。可见氩气的电子密度峰值不受占空比的影响,持续时间正比于占空比。对比图2(a)和图2(b),可见在相同占空比下空气的电子密度峰值低于氩气的。
将占空比固定为50%,随着E/N的增加,空气与氩气的平均电子温度都逐渐增大,但是空气的平均电子温度增长速率逐渐变大,氩气的平均电子温度增长趋势较为稳定。对比空气与氩气,可以看出在约化电场强度相同的前提下,空气的平均电子温度低于氩气的平均电子温度。
将E/N固定为55 Td,随着占空比的增加,空气与氩气的平均电子温度都逐渐增大,且增长趋势逐渐变缓。对比空气与氩气,可以看出在占空比一致的前提下,空气的平均电子温度低于氩气的平均电子温度。
2.2 约化电场强度和占空比对平均粒子密度的影响
将占空比固定为50%,在45~65 Td范围内调节约化电场强度,模拟空气与氩气微波放电粒子的产生,仿真结果如图3所示。
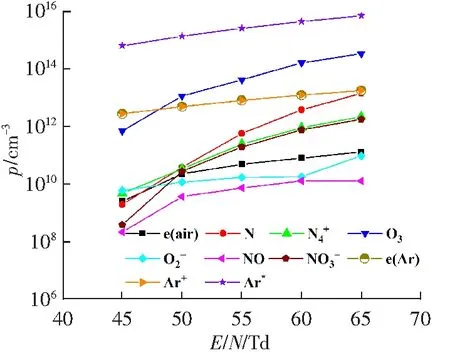
图3 不同E/N下平均粒子密度图Fig.3 Average particle densities at different E/N values
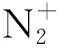
氩气中的平均电子密度变化趋势与空气中的相一致,但是其数值要高于空气的平均电子密度,Ar+的平均粒子密度与氩气的平均电子密度重合,在氩气介质中,Ar的平均粒子密度最高。
将E/N固定为55 Td,占空比在10%~90%范围内进行调节,模拟空气与氩气微波放电粒子的产生,仿真结果如图4所示。
从图中可以看出,随着占空比的增加,大部分粒子密度呈现平缓增加的趋势。当占空比小于30%,粒子密度上升较快,大于30%后,上升趋缓。可见当占空比大于30%后,占空比的增加对等离子体中平均粒子密度的影响变小。
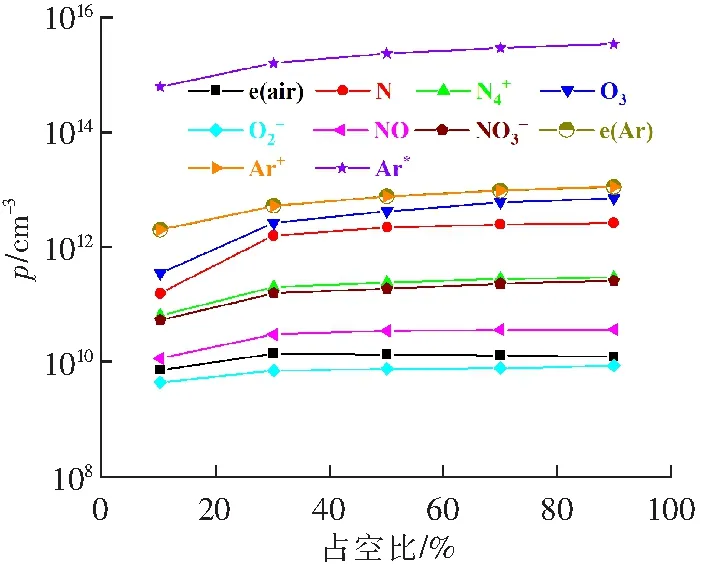
图4 不同占空比下平均粒子密度图Fig.4 Average particle densities at different duty cycles
由图4可见,氩气的平均电子密度高于空气的平均电子密度。氩气介质中Ar的平均粒子密度最高,氩气的平均电子密度与Ar+的平均粒子密度重合。仿真结果表明,改变占空比对平均粒子密度的影响不明显,特别是占空比达到30%之后。
2.3 空气中粒子反应路径
空气微波放电等离子体中粒子种类较多,为了进一步研究粒子的演化特性,理解整个反应体系,我们画出了空气中主要粒子的反应路径图,如图5所示。其中E/N为55 Td、占空比为50%,图中对应的百分数为参与反应的粒子占粒子总量的百分比。从图5可以看出,N2(A)、N2(B)、N2(C)等激发态粒子主要来自于电子与氮气的电子碰撞激发反应。
在空气微波放电等离子体反应过程中,53.92%的N2通过电子碰撞激发反应生成N2(B),25.55%的N2通过电子碰撞激发反应生成N2(A),11.54%的N2通过电子碰撞激发反应生成N2(C),还有6.14%的N2通过反应生成N2(a′)。
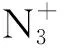

图5 空气中粒子反应路径图Fig.5 Diagram of particle reaction paths in air
3 结论
本文采用空气与氩气零维微波放电等离子体模型,研究了约化电场强度对电子密度和平均粒子密度的影响。仿真结果表明,空气中的电子密度峰值随着约化电场强度的增加而增大,随着占空比的增加而减少;氩气中的电子密度峰值随着约化电场强度增加而增大,但不随占空比的变化而改变。相同约化电场强度下,空气的电子密度峰值低于氩气的。多数粒子的平均粒子密度随着约化电场强度的增加而增大,随占空比的增加呈现增大趋势,但变化不明显。相同条件下,氩气等离子体的平均电子密度高于空气的。
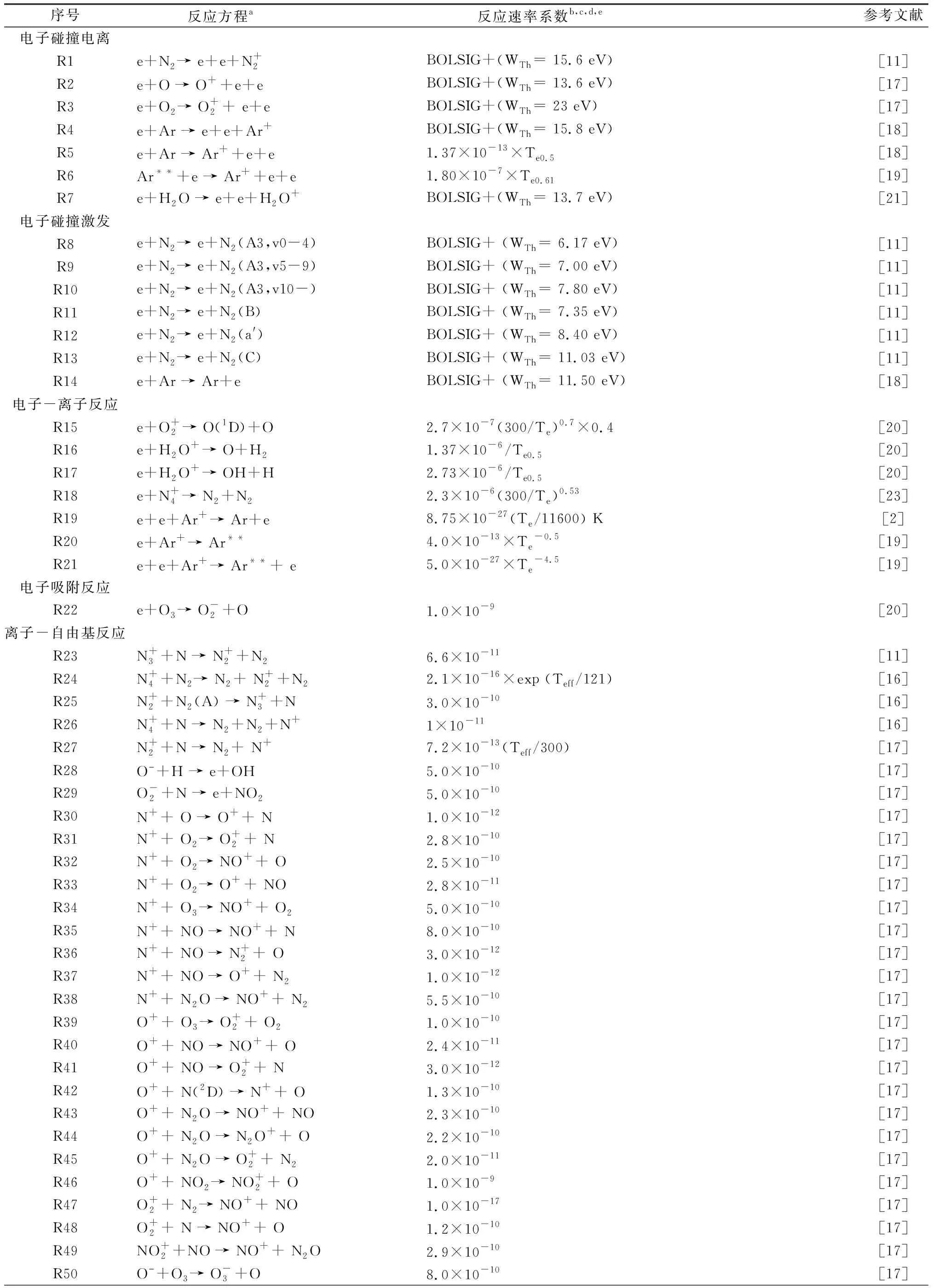
附录 气相反应及其反应速率系数

续附录 气相反应及其反应速率系数

续附录 气相反应及其反应速率系数

续附录 气相反应及其反应速率系数

续附录 气相反应及其反应速率系数
