真三轴压缩下大理岩强度、变形与损伤特征数值

2022-07-05王浩然王志亮王昊辰汪书敏

哈尔滨工业大学学报 2022年8期

王浩然，王志亮，王昊辰，汪书敏

(合肥工业大学土木与水利工程学院，合肥 230009)

自然界中岩体处于复杂应力状态，在进行深部洞室开挖过程中，临空面会释放岩体中积累的应变能，造成应力重分布，导致岩体内部产生新裂纹，并且裂纹与裂纹之间扩展贯通，最终会造成岩体的失稳破坏[1-3]。以往的常规三轴压缩试验忽略了中间主应力(σ2)的影响，传统的莫尔-库仑和霍克-布朗准则对真三轴应力状态下岩石力学表征难以适用，而中间主应力对岩石在真三轴应力状态下的力学特性影响显著[4]。近年来，许多学者对深埋大理岩进行真三轴压缩试验，以探究其在高地应力下的破坏机制。Zheng等[4]探讨了锦屏大理岩在真三轴压缩下的残余强度特征，发现对于较高σ3(最小主应力)，随着σ2的增大残余强度先减小后增大，对于较低σ3，则随着σ2的增大而逐渐减小；Feng等[5]对花岗岩、大理岩和砂岩等进行了真三轴循环加卸载试验，指出岩石黏聚力对σ3和σ2不敏感，内摩擦角最小值不受σ3和σ2的影响，但其最大值受两者的影响；Gao等[6]对含节理的锦屏大理岩进行真三轴压缩试验，发现节理大理岩强度对σ3的敏感性要大于对σ2的敏感性。

然而，在实验室进行真三轴试验需要先进且昂贵的实验设备，试件的制备也费时耗力，并且试验中很难观察到细观的破坏过程。近年来，数值模拟方法已成为传统研究方法的有力补充。其中，离散单元法作为一个有效的数值分析工具，广泛应用于岩石力学研究[7-8]。Yang等[9]研究了射孔角度和射孔布置对同步水力压裂裂缝扩展机制和岩石破坏模式的影响，指出大主应力差下较小的射孔间距更有利于中心岩体的破裂。Lee等[10]对非平行双裂隙花岗岩试样进行单轴压缩试验，并且开展了颗粒流程序模拟，发现岩桥裂纹的贯通主要通过拉伸裂纹的扩展聚集。Zhang等[11]对含两个平行裂隙的矩形类岩石试件进行单轴压缩数值模拟，总结出岩桥贯通两种新模式。由于实际工程问题复杂，简化为二维问题后，其计算结果存在一定差距，故开展三维数值研究十分必要。Duan等[12]对砂岩展开真三轴压缩离散元模拟，重点分析σ3、σ2对微裂纹取向、黏结力取向、组构和配位数演化的影响，指出随着σ3水平的增加，σ2对颗粒尺度响应的影响逐渐减弱。Zhang等[13]采用平行黏结模型先标定大理岩的力学性能，然后建立真三轴压缩数值模型，在数值岩样上预制裂隙，研究裂隙大理岩在真三轴应力状态下的破坏特征。Zhang等[14]采用黏结粒子模型研究花岗岩在真三轴应力状态下的变形和强度特征，消除了端部效应，隔离了中间主应力的影响。

综上，中间主应力对岩石力学特性影响较大，且目前对真三轴应力环境下的岩石内部裂隙扩展演化过程难以做到实时观察。为此，拟采用三维离散元颗粒流程序(PFC3D)对大理岩试件开展真三轴应力状态下的微观裂纹扩展机制数值研究，并基于全应力-应变曲线特征，深入探析裂纹扩展过程与受压变形过程当中的内在联系，同时与实验观测结果进行比较，力求得出具有参考价值的结论。

1 数值模型的建立

1.1 数值模型

PFC5.0内嵌有十种接触模型[8]，其中，平行黏结模型在模拟岩石类材料受压破坏时，能够沿着法向或者切向破坏，可较好地反映此类材料的破坏形式，已广泛应用于岩石类材料相关问题分析中[15]，故本文选择该模型进行后继研究。大理岩试样数值模型尺寸为50 mm×50 mm×100 mm，假定无内部缺陷。采用与文献[16]常规三轴压缩数值试验相同的平行黏结模型细观参数，大理岩颗粒的半径在0.9～1.356 mm，避免颗粒尺寸对力学性能的影响。其中，真三轴数值模型包含26 018个颗粒，112 093个平行键黏结，4 504个线性黏结，如图1所示。

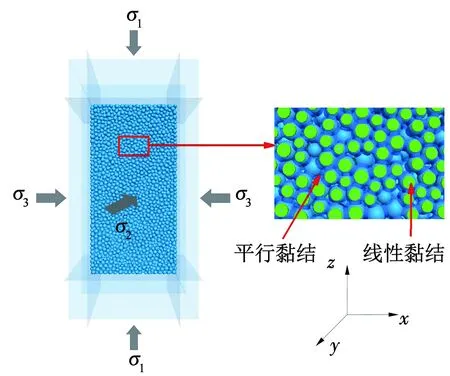
图1 数值建模

1.2 真三轴压缩模拟加载方式

数值模拟中的加载应力路径是仿照岩石真三轴压缩试验的加载方式[17-18]，如图2所示，模拟的加载路径由以下3个阶段组成：

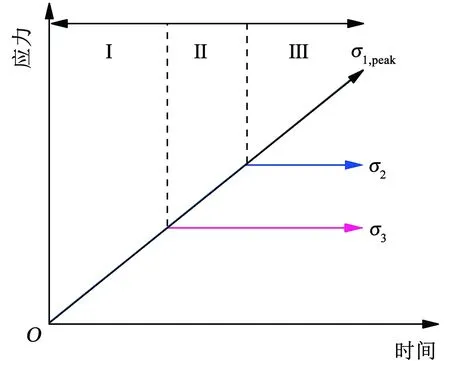
图2 真三轴试验的加载路径

1)在静水条件下(σ1=σ2=σ3)，通过伺服控制函数控制6个墙体以一定位移速率单调加载试样，直到达到预设的σ3水平。

2)通过伺服控制函数控制x方向上两个平行墙体保持σ3恒定，同时控制y、z方向两对平行墙体以恒定位移速率继续加载，保证σ1和σ2以相同的速率单调上升，直到达到预定的σ2。

3)通过伺服控制函数控制x、y方向上两对平行墙体保持σ2、σ3恒定，控制z方向平行墙体保证σ1单调升高，直至峰值(σ1,peak)，然后继续加载至σ1后下降到σ1,peak的70%时终止。

1.3 真三轴模拟应力路径及破坏角的测量

对大理岩数值试样分别进行7组不同应力控制的真三轴压缩破坏试验，即将最小主应力σ3分为5、20、50、80、100、120和150 MPa 7个应力水平，每个应力水平下，σ2的大小根据模拟过程中峰值强度确定，涵盖了从σ2=σ3到σ2=σ1的整个范围(表1)。

表1 大理岩真三轴模拟的破坏应力状态和破坏面角

图3展示出破坏面角度θ的测量方法，左边为颗粒破坏后的fragment显示(同种颜色的颗粒表示同种破碎块体)，中间为微裂纹的空间分布(深色为剪切裂纹，浅色为拉伸裂纹)，右边为颗粒位移矢量空间分布。当σ2=σ3时没有明显的破坏角；当σ2>σ3时，平行黏结键断裂，无法传递力，故无法形成力链，则在平行黏结键断裂处产生微裂纹，微裂纹的积累导致破裂面的产生。而且，破坏面平行于中间主应力方向，各个应力路径下破坏角的范围为60°～65°(见图3(b)、表1)，对于恒定σ3，破坏角随着σ2的增大而增大。

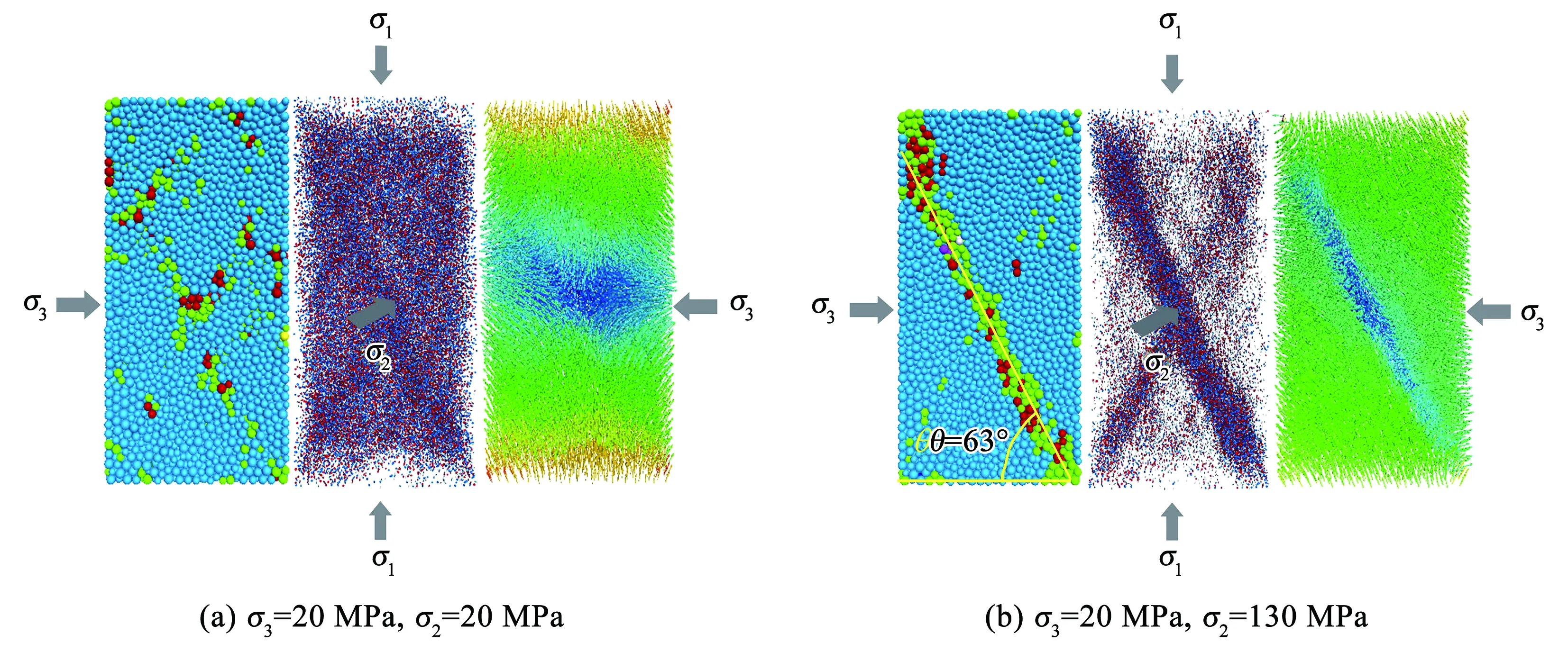
图3 PFC计算结果及破坏角的测量

2 真三轴压缩数值结果分析

2.1 中间主应力对真三轴破坏应力的影响

表1列出了破坏时的所有真三轴压缩应力条件，对于每个最小主应力σ3，σ1,peak是σ2的函数，如图4所示。可以看出，σ1,peak随σ2的增加而增大，且当σ2达到某一固定平台值时，超过此值σ1,peak逐渐下降，这种变化趋势不是左右对称的，相关硬岩真三轴压缩试验结果一致[19-20]。

由上可知，σ1,peak既是σ3的函数，又是σ2的函数。σ1,peak这种先升后降的趋势符合二阶多项式方程特征。曲线图4中的虚线组成常规三轴压缩(σ2=σ3)和常规三轴拉伸(σ2=σ1)两种极限情况，σ1,peak与σ3的变化可以用下式来线性拟合，这实为传统的三轴破坏判据，即Mohr-Coulomb准则。

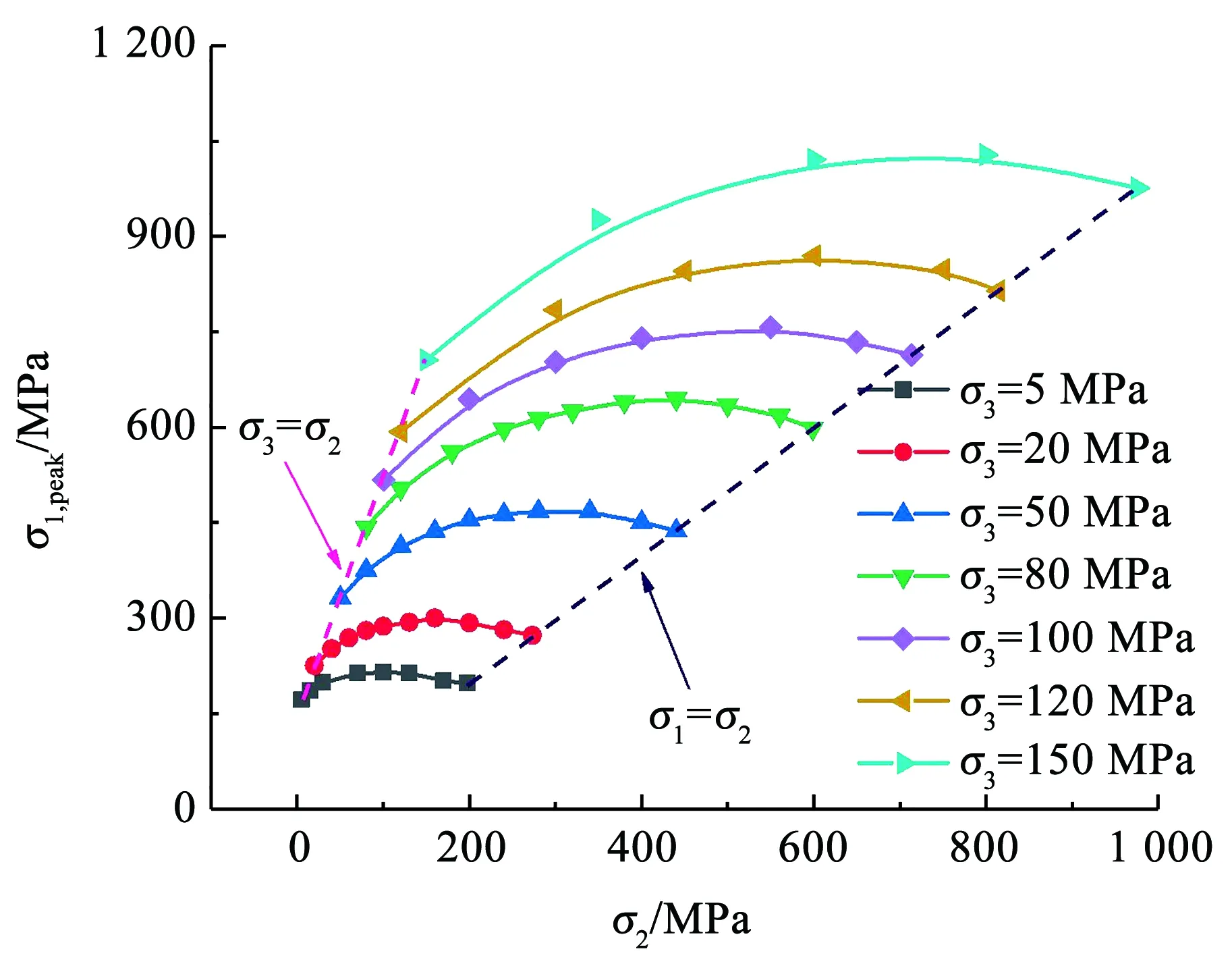
图4 σ1,peak与σ2在恒定σ3水平上的变化关系

对于常规三轴压缩(σ2=σ3)

σ1,peak=150.84+3.68σ3,R2=0.999

(1)

对于常规三轴拉伸(σ1=σ2)

σ1,peak=169.28+5.40σ3,R2=0.999

(2)

对于给定的σ3，σ1,peak与σ2的关系曲线表现出强度上的差异性，这揭示了传统的三轴压缩试验以及经典莫尔-库仑和霍克-布朗等破坏准则存在不足。

取峰值应力50%处的割线模量计算岩样的弹性模量E，图5展示E在σ3应力水平下随σ2的变化关系，可以看出，在每个最小主应力水平下，弹性模量随着中间主应力的增加先急速增加，再逐渐趋近于平稳，并且最小主应力越大，平稳增加段所占比例就越大，表明最小主应力对弹性模量的增加有约束作用。采用Logistic函数可直观表示E和σ2的变化关系，拟合方程列于图5中，拟合度较高。

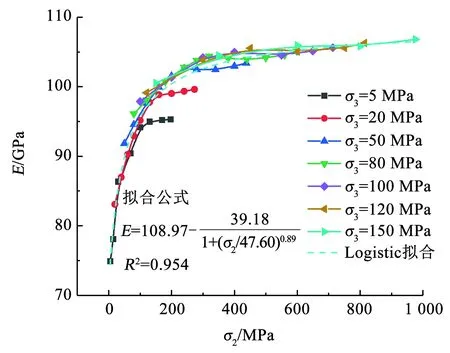
图5 E与σ2在恒定σ3水平上的变化关系

2.2 基于八面体理论的真三轴破坏应力分析

八面体理论认为，当岩石内部八面体剪应力达到某一临界值时，岩石将进入破坏阶段。为了研究大理岩试样的空间破坏特性与中间主应力之间的关系，并且表1和图4真三轴破坏时的应力状态都可以由两个主应力不变量之间的单一关系表示，即破坏时的八面体剪应力(τoct,f)和破坏时的八面体正应力(σoct,f)：

τoct,f=[(σ1,peak-σ2)2+(σ2-σ3)2+

(σ3-σ1,peak)2]1/2/3

(3)

σoct,f=(σ1,peak+σ2+σ3)/3

(4)

图6(a)是在τoct,f-σoct,f区域中重新绘制破坏时的应力条件，可以看出，在大理岩数值试样当中，τoct,f随着σoct,f的升高而持续上升，尽管上升速率有所下降。因为所建数值模型没有明显缺陷，破坏时的主要原因是剪切而不是压实[21]，与2.4节的结论相同。同时，为了更好地确定在恒定σ3应力条件下σ2在σ1和σ3之间的相对位置，引入应力比b[17]，对于确定的破坏应力状态，可以获得良好的数据基础。应力比b定义为

b=(σ2-σ3)/(σ1-σ3)

(5)

对图6(a)中所示的数据点进行二阶多项式方程拟合，得到式(6)的τoct,f-σoct,f变化方程。

(6)

由图6(b)可以看出，在τoct,f-σoct,f曲线区域中数据点表现出一定的分散性，但是分散中包含潜在规律，即对于每个级别的τoct,f，最小的σoct,f一致地出现在σ2=σ3时，最大的σoct,f一致地匹配σ2=σ1应力状态。

在图6(c)中，重新绘制了与图6(a)和(b)相同的应力状态数据点，从式(5)可看出,σ2=σ3和σ2=σ1时，应力比b=0和b=1。与此同时，图6(c)为每个数据点分配了与其表示的b值相对应的颜色(侧面显示的颜色条)，易见低σ3下个体b的离散度非常低，σ2=σ3和σ2=σ1的拟合曲线(图中虚线)明确地描绘b=0和b=1时的应力状态，即分别对应岩石处于广义三轴压缩状态(σ1>σ2=σ3)和广义三轴拉伸状态(σ1=σ2>σ3)。对比图6(a)和(c)可以看出，对于0到1的任何其他b值，都可以得到一条拟合良好的曲线，并且对于恒定的b值，τoct,f随着σoct,f线性增加，形成线性的破坏包络线。

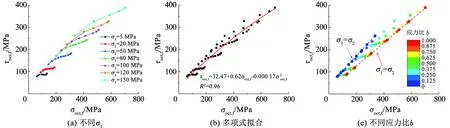
图6 破坏时τoct,f随σoct,f的变化

2.3 变形特征与裂纹扩展的联系

图7给出了σ3=150 MPa下的偏应力与3个主应变分量的关系。限于篇幅，仅讨论一个最小主应力水平下的关系图。易见随σ2/σ1的增大，应变εy由拉应变转为压应变，并且压应变也随之增大。增加σ2/σ1值也会导致在最小应力方向上位移膨胀量的提升。在第1个拐点之前，3个主应力、主应变大小相同，压缩方向一致且为正；在第1个拐点与第2个拐点之间，最大主应力和中间主应力大小相同，εz和εy由于两个方向的压缩而一致且为正，εx由于在该方向上开始扩张而为负；第2个拐点之后，εy与εz由重合变为分离，两个方向上的应变变化较为明显。

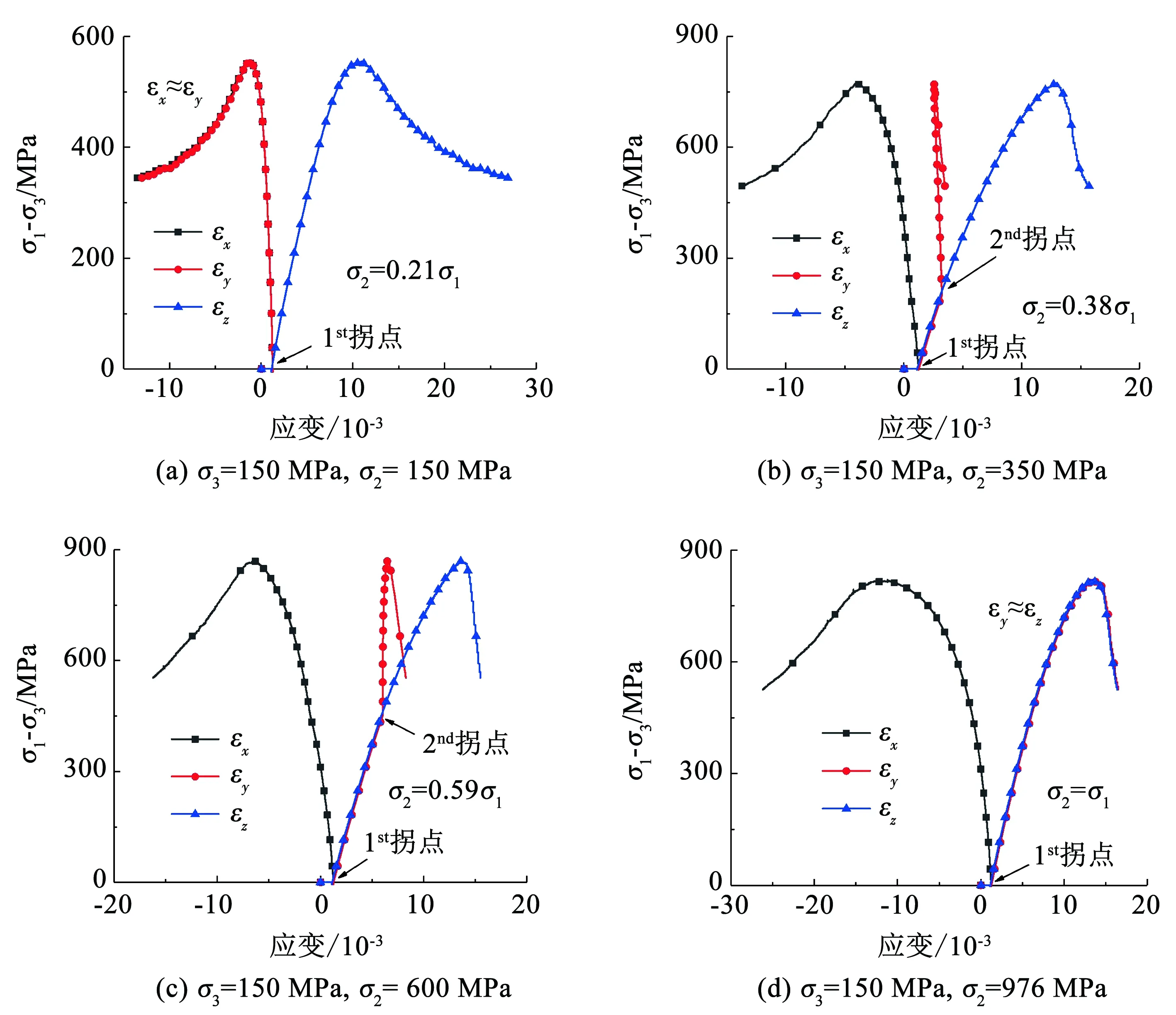
图7 不同应力路径的偏应力-应变关系

图8展示出σ3在80 MPa下微裂纹数量、每10时步所产生的微裂纹数和偏应力与轴向应变的关系。对比常规三轴压缩偏应力-应变曲线，真三轴大理岩破坏微裂纹的演化过程也可分为4个阶段：第1个阶段为线弹性阶段(OB段)，其中3个主应力伺服至σ3时到达A点，数值试样不断被压缩，包含初始压密区，几乎没有微裂纹和声发射事件产生，B点所对应的偏应力在40%σ1,peak附近；第2个阶段为裂纹稳定扩展阶段(BC段)，试样声发射事件呈稳定增长态势，岩石损伤呈稳定速率上升，C点所对应的偏应力在80%σ1,peak附近；第3个阶段为裂纹非稳定扩展阶段(CD段)，D点对应峰值强度，从C点新生裂纹张开度明显增大，岩样出现不可恢复的塑性变形，并且随着σ2增加该阶段占比增大；第4个阶段为峰后破坏阶段(DE段)，D点之后，不同应力条件下微裂纹的扩展速率不尽相同，但是随着宏观裂隙的形成，该阶段后期的微裂纹扩展速率逐渐降低。

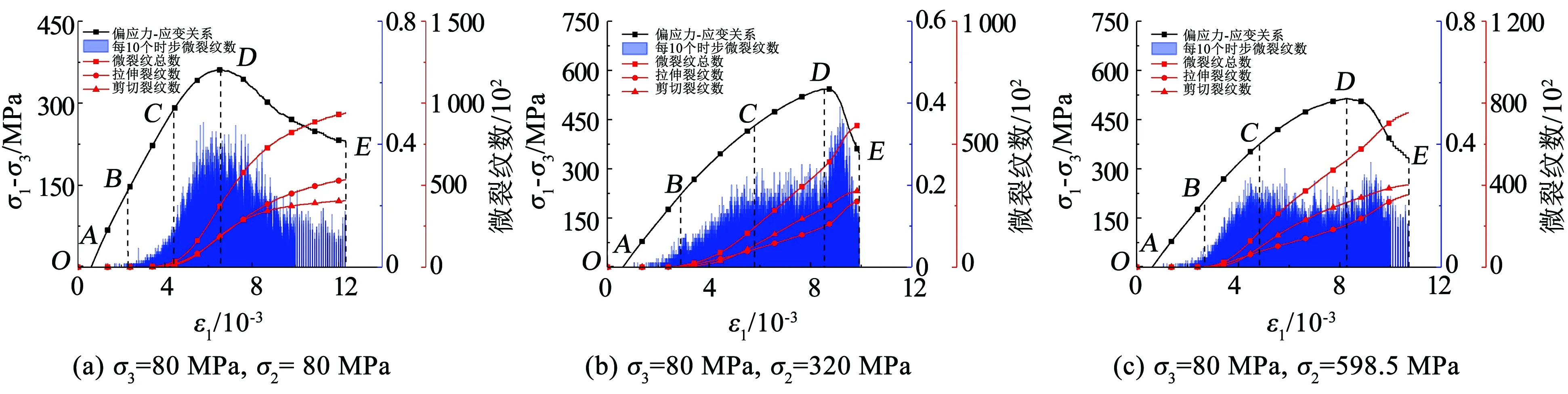
图8 轴向应变与偏应力、微裂纹数和声发射的关系

从图8可以看出，随着σ2的增大，试样峰后表现出由塑性破坏转向脆性破坏的趋势。当σ3保持不变时，随着σ2增大CD阶段所占比重增加，并且剪切裂纹数目慢慢大于拉伸裂纹数目，破坏方式从拉伸破坏转变为拉剪混合破坏。对于恒定的σ3，不同应力路径下σ2的大小影响微裂纹的产生速度，即损伤的变化速率，且σ2越大则峰后损伤速率下降得越快。

2.4 微裂纹形成对宏观破裂面的影响

图9为不同应力路径下微观裂纹倾向倾角与其相对数量关系的赤平极射投影。对比图9(a)与(d)可看出，初始围压对微观裂纹的倾向倾角有较大影响：初始围压较低时微观裂纹倾向分布较均匀，裂纹主要平行于最大主应力方向，类似单轴压缩时裂纹的赤平极射投影[22]；σ3=σ2=80 MPa属于初始围压较高的状态，裂纹的倾向开始往中间主应力方向(90°)和最小主应力方向(0°)上集中，并且裂纹的倾角慢慢变大。从图9(b)和(c)可以看出，因σ2>σ3时出现明显的破坏角，裂纹倾向以及数量分布从中间主应力方向逐渐向最小主应力方向扩展，并且随着中间主应力的增大，裂纹倾角也慢慢偏离最大主应力方向，最终扩展的角度形成实际的宏观破坏角(位于60°～65°)。

图9 细观裂纹赤平极射投影

从图10(a)可以看出，对于低σ3应力水平，拉伸裂纹占比较大；当σ3>50 MPa之后，随着σ2增大，剪切裂纹占比开始增大，破坏方式从拉伸破坏向拉剪混合破坏转变。在图10(b)和(c)中，对于恒定的σ3，微裂纹数目随σ2先下降然后再上升，岩样损伤发展呈现出“对勾”型变化趋势，即开始下降快，而上升速度滞缓。当σ3=σ2时，随着σ3的增大，微裂纹数目快速上升；而当σ1=σ2时，随着σ3的增大，微裂纹数目上升速率较为缓慢，后期微裂纹数目几乎没有变化。从这两图中的虚线可以看出高中间主应力抑制损伤的上升趋势。