阿克苏地区日蒸散量估算方法研究

2022-07-05何南腾邹嘉南郭文弟周笑迁

气象研究与应用 2022年2期

何南腾，邹嘉南*，郭文弟，周笑迁，狄迪

（1.南京信息工程大学中国气象局气溶胶与云降水重点开放实验室，南京 210044；2.中国地质调查局西安矿产资源调查中心，西安 710100）

引言

蒸散发是陆面水循环中重要的水文过程之一，也是联系植物碳交换和水分利用的关键生态过程［1］。作为大气和地表之间的联系，蒸散量作为水文参量同时出现在地表水量和能量平衡方程中，是陆面过程数值模拟研究中不可缺少的重要边界条件。此外，Rosenberg 等［2］认为70%降落到地球表面的降水是通过蒸发或蒸散作用回到大气中的，在干旱区这个比例可达90%。因此，它对于了解作物蒸散发过程规律、水资源管理以及提高水资源利用效率以及干旱评定等［3-5］有重要意义。近年来，Santos 等结合遥感技术与土壤水量平衡模型，估算了西班牙西南地区棉田2004—2005 年蒸散量的季节变化［6］；Nobuhiro 等通过能量平衡波文比方法估算了常绿阔叶林蒸散发［1］；Zhao 等基于多年涡度相关和小气候梯度系统观测数据库，使用了土壤水量平衡法、波文比法、Penman－Monteith（PM）等6 种方法估算并比较绿洲农田蒸散量，发现Penman－Monteith（PM）结果最符合绿洲实际［7］。由于受不同地区气象和地形、地貌时空异质性的影响，不同参考作物蒸散量计算公式的适用性各不相同。Penman－Monteith（PM）公式作为FAO 专家组唯一推荐使用的参考作物蒸散量计算公式，至今多种参考作物蒸散量计算方法的适用性评价已成为当今的热点问题。然而，参考作物蒸散量计算方法的普适性在极端干旱区却鲜有研究。本文依据阿克苏地区2006—2015 年日蒸散量数据与气象资料，对Penman－Monteith（PM）公式进行进一步的优化与适用性分析，以期推荐一个更加精确的参考作物蒸散量计算方法，这对于了解极端干旱区棉田等作物种植以及可持续发展有长远的意义。

此外，由于气象数据具备周期性强、时空性、多维多尺度、各属性相互影响等特征，仅用传统方法对气象数据进行分析和处理会遇到诸多困难［8］。目前，由于遥感卫星成本低，基于遥感技术和模型估算蒸散发逐渐成为一种经济实用的手段［9-10］。另外，神经网络作为一种人工智能算法，有别于传统方法，特别是应用在处理非线性问题上有着良好效果。此前，也有专家利用神经网络模型模拟膜下滴灌玉米逐日蒸散量［11］。本研究利用了反向传播神经网络（Back Propagation Neural Network，下文统一称为BP 神经网络）、广义回归神经网络（General Regression Neural Network，下文统一称为GRNN 神经网络）两种神经网络对日蒸散量数据进行拟合，希望通过此寻找出一种较为准确的日蒸散量估算方法。

1 资料与方法

1.1 研究区概况

阿克苏地区位于新疆中部地区、天山山脉中段南麓、塔里木盆地的北缘，78°03′～78°39′E，39°30′～42°41′N，面积约为1325×104hm2。综合观测场位于阿克苏站区内，地理坐标：80°45′E、40°37′N，海拔1028m，2006 年建立，长方形，大小150m×90m，可以满足100a 尺度的采样要求。

1.2 数据来源

本研究使用了阿克苏站中综合观测场农田生态系统2006—2015 年有测量记录的日蒸散量数据（100 个样本，水量平衡法，单位mm·d-1，来自国家生态科学数据中心资源共享服务平台（http：／／www.cnern.org.cn／），在本研究中用于日蒸散量估算值的对比与验证。另外，使用了相匹配日期的阿克苏站的气象资料，包括日平均气温、日最高气温、最低气温、日照时数、平均相对湿度、平均水汽压、平均风速等气候要素观测数据和经纬度、海拔高度等地理数据。由于国家生态科学数据中心资源共享服务平台中没有阿克苏站以上需求的日尺度气象资料，所以，本研究需要的气象资料引用了美国国家海洋和大气管理局（NOAA）国家环境信息中心（NCEI）相应的日尺度数据。

对于Penman-Monteith（PM）公式和GRNN 神经网络、BP 神经网络，为方便对估算方法的评估，本研究采用同样的样本进行对比。其中，Penman-Monteith（PM）公式包括了所有样本的计算，GRNN 神经网络、BP神经网络验证集中的30 个样本在总样本中随机选出。

1.3 计算方法

1.3.1 Penman-Monteith（PM）公式

在蒸散量计算中，彭曼法（Penman-Monteith）基于能量平衡和水汽扩散理论，不受作物种类、土壤类型和水汽条件等因素的限制，仅考虑气候要素的影响，其计算得出的潜在蒸散量与实测值最为接近，因此被广泛应用到区域干湿状况的评价研究中［12］。表达式如下：

式中，PE 为潜在蒸散量，Δ 表示空气气温为T时的饱和水气压斜率，计算方式如（2），本次研究中T 取日平均气温，Tmean表示日平均温度（℃），es表示饱和水气压（kPa），ea表示实际水气压（kPa）；Rn为地表净辐射，等于收入短波辐射Rns 和支出的净长波辐射Rnl 之差；G 为土壤热通量，一天至十天的时间尺度，其参考草地的土壤热容量相当小，可以忽略不计。γ 为干湿表常数，计算方式如（4），其中P 为大气压；u2为2m 高风速，uz表示10m 高处风速，z 表示高度，取10m。

1.3.2 方法校准

在日蒸散量计算中，主要对地表净辐射项的参数做出调整。目前对于地表净辐射有诸多经验方法已被广泛用于估计世界各地的净辐射，然而，这些经验方法需要特定地点的参数校准。Xiao 等［13］量化了地表反照率的时空变化以更好地估计中国地区的净短波辐射，并基于原位观测重新校了FAO-56 PM方法的参数以更好地估计净长波辐射。此方法也可用于彭曼法（Penman-Monteith）对日蒸散量的计算。地表净辐射等于收入短波辐射Rns 和支出的净长波辐射Rnl 之差。对于短波辐射有：

其中，RS为太阳辐射，对于阿克苏地区（40°37′N），校准后有：

其中α′随月份变化如表1 所示

表1 阿克苏地区地表反照率随月份变化

此外，对于净长波辐射Rnl 有

其中，σ＝4.903×10-9为斯蒂芬-玻尔兹曼常数（MK·K-4·m-2·d-1）。分别为最高和最低绝对气温（K＝℃＋273.16）；ea为实际蒸汽压；RS为太阳辐射，RS0为晴空辐射；a、b 为经验回归系数（无量纲）。

对于阿克苏地区a＝0.50－0.002×lat＝0.419，b＝－0.25＋0.002×lat＝－0.169。所以对于修正后的地表净辐射项可列为：

1.3.3 神经网络

（1）GRNN 神经网络

GRNN 具备很强的非线性映射能力、柔性结构以及较好的容错性，适用于解决非线性问题。GRNN在逼近能力和学习速度上也有很强的优势，网络最后收敛于样本量积聚较多的优化回归面，另外在样本数据较少时，也有一个较好的预测效果。

GRNN 神经网络由四层构成［14］。如图1 所示，分别为输入层、模式层、求和层和输出层。假设样本特征集为：｛trx1，trx2，…，trxm｝，其中trxi＝［x1，x2，…xn］。标签集为：｛try1，try2，…，trym｝，其中tryi＝［y1，y2…，yk］。

输入测试样本，节点个数等于样本的特征维度。模式层中节点个数等于训练样本的个数，第i 个测试样本trxi与第j 个测试样本trxj之间的Gauss 函数取值为：

求和层节点个数等于输出样本维度加1×（k＋1），求和层的输出为两部分，第一个节点输出模式层输出的算术和，其余k 个节点的输出为模式输出的加权和。假设对于测试样本tex，模式层的输出为｛ɡ1，ɡ2，…ɡm｝。

求和层第一个节点的输出为：

其余k 个节点的输出为：

其中加权系数yij为第j 个模式层节点对应的训练样本的标签的第j 个元素。

输出层节点个数等于标签向量的维度，每个节点的输出等于对应的求和层输出与求和层第一个节点输出相除。

（2）BP 神经网络

本次研究还采用了BP 神经网络（如图2），其含有输入层、隐含层和输出层三个部分。BP 神经网络使用梯度下降算法［15］。假设输入层神经元为P＝［p1，p2，…，pi］，隐含层神经元为S＝［s1，s2，…，sk］，输出层神经元为Y＝［y1，y2，…，yj］。另外，表示输入层第i 个神经元连接隐含层第k 个神经元的权值，表示隐含层第k 个神经元连接输出层第j 个神经元的权值。隐含层的激发函数为f1，输出层的激发函数为f2，表示隐含层神经元阈值，表示输出层神经元阈值，其中，∈（－1，1）。

输入层各神经元与隐含层各神经由相应的权值连接，隐含层的第一个神经元x1，加权求和从输入层每一个神经元处得到输出值，加上阈值，通过激发函数f1，得到该神经元的输出值：

然后，输出层第一个神经元y1 接收隐含层每一个神经元输出值，并加权求和得，加上阈值，通过激发函数f2，得到输出层该神经元的输出值：

（3）评估方法

拟合优度指标通常用于评价改进方法的性能，通常对于此类研究采用Nash-Sutcliffe 系数（NSE）、平均偏差误差（MBE）和均方根误差（RMSE）。表达式如下［13］：

式中n 为观测次数；Re为估计数据；R0为观测数据；Rave为观测数据的平均值。Nash-Sutcliffe 系数取值范围为-∞～1，其值越接近1，均方根误差值越小，模型性能越好。平均偏差误差为正值表示高估了结果，其为负值则表示低估了结果。

2 结果与分析

2.1 自相关性分析

表2 为日蒸散量与日最高温度、日最低温度、露点温度、风速、日照时长、降雨量等六个气象要素相关系数的统计。其中，p 值表示原假设为真时得到的样本观察结果或者更极端结果出现的概率。* 表示有统计学差异（p＜0.05），** 表示差异显著（p＜0.01），显著性差异。它是统计学上对数据差异性的评价。通常情况下，实验结果达到0.05 水平或0.01 水平，才可以说数据间具有差异显著或是极显著。

从表2 中可以看出，日蒸散量与其他六个气象要素量均呈正相关，与日最高温度、日最低温度和日平均露点温度相关系数分别为0.3142、0.4338、0.4624，且均达到0.01 显著性水平。神经网络对结果的预测如果是建立在具有高度相互影响的因素上，其预测模型和结果会相对可靠，综合彭曼公式和相关系数考虑，本研究利用日最高温度、日最低温度、日平均露点温度、风速、日照时长、纬度、海拔、日序作为自变量，日蒸散量作为因变量，建立神经网络模型。

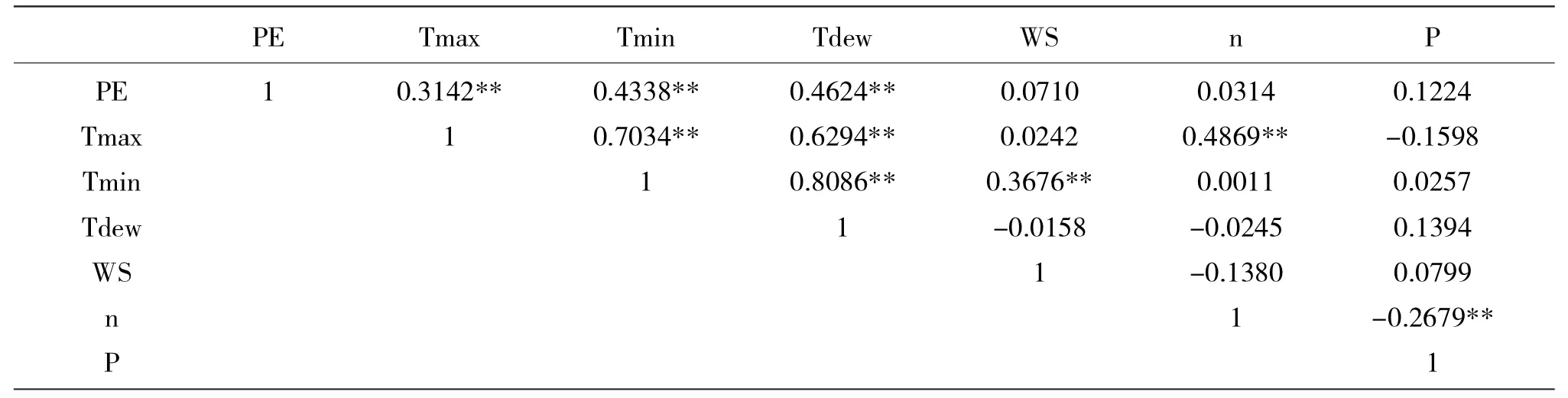
表2 自相关性分析

2.2 修正后彭曼法（Penman－Monteith）

如图3 所示，修正过后彭曼公式对于日蒸散量的估算比修正前要小（MBE 值由8.4428 减小到5.6030），且更接近于真实测量值。从拟合效果来看，Nash-Sutcliffe 系数修正前与修正后分别为0.0328与0.0132，能说明结果接近观测值的平均值水平，总体结果可信。同时，修正前后的均方根误差分别为11.7830 和8.7981。所以总的来说，修正后彭曼公式效果优于修正前，对阿克苏地区日蒸散量计算的适用性和准确性相比修正前有所增加。

2.3 GRNN 与BP 神经网络估算

此次研究使用了一百个样本，分成70 个训练集与30 个测试集，使用了日最高温度、日最低温度、露点温度、风速、日照时长、纬度、海拔、日序等八个变量作为输入值，日蒸散量作为输出值。将GRNN 神经网络拟合结果与实际测量值进行评估，其Nash－Sutcliffe 系数为－0.4410，均方根误差为3.3431，说明结果接近观测值的平均值水平，总体结果可信。另外，测试集中仍有少部分预测值（4 个）与测量值相比有较大误差。这涉及到神经网络的泛化性问题，此次研究的训练样本数量较少，导致有少量较大误差的预测值产生。

对于BP 神经网络，为取消样本数量对拟合效果的误差，同样分成70 个训练集与30 个测试集，使用了日最高温度、日最低温度、露点温度、风速、日照时长、纬度、海拔、日序等八个变量作为输入值，日蒸散量作为输出值。估算结果与实际值的Nash－Sutcliffe 系数为－0.0883，均方根误差为3.2659，总体结果可信。其中仍有少量的预测值与测量值相比有较大误差。另外可以看出，BP 神经网络较GRNN 神经网络对日蒸散量估算有更好的效果。

经过对比，BP 神经网络对于日蒸散量的估算效果优于GRNN 神经网络。所以对于BP 神经网络，本研究做了进一步的评估。图4 显示神经网络输出对训练、验证和测试集的目标回归图。四幅图的y＝x 线表示目标输出，不同颜色的实线表示神经网络输出。为了完美的配合，数据应该沿着45 度的线下降。可以看出训练集与验证集输出值贴近目标值，且回归系数分别达到0.94244 和0.94606。同时，测试集回归系数为0.6113，效果不如训练集与验证集，本研究认为是由数据量偏少造成。另外，总体的输出值与目标值也贴近且回归系数达到了0.90871，证明BP 神经网络对于日蒸散量的估算问题上，有一个很好的拟合效果。