K-means+SSA-Elman网络可见光室内位置感知算法

李宝玉，张 峰，彭 侠，刘叶楠

（1.西安工业大学 电子信息工程学院，陕西 西安 710065；2.西安应用光学研究所，陕西 西安 710065）

引言

随着无线定位的发展，位置感知服务市场应用前景日益广阔[1-2]。可见光(visible light, VLC)室内位置感知具有成本低、定位精度高、噪声干扰小等优点[3-4]。在基于场强、聚类和神经网络等室内位置感知算法中[5]，神经网络在VLC室内位置感知中具有训练速度快、耗时短等优点。其中，基于Elman网络的算法具有适应时变特性、计算能力强等特点，但也存在预测值易陷入局部最优、收敛速度慢等问题[6]。文献[7]将遗传算法融入粒子群算法中，确定Elman网络权阈值，建立训练模型，提高预测精度，但需大量训练样本，操作繁琐；文献[8]通过灰狼优化算法对Elman网络进行优化，确定最优权阈值，提高模型预测精度；文献[9]采用EMD将数据分解为有限个子函数，建立Elman子模型，利用粒子群算法对权值进行寻优操作，但精度提升有限。

论文利用SSA对Elman神经网络权阈值进行优化，使网络获得最优参数，从而达到提高定位精度的目的。在此基础上融合K-means算法，利用K-means对数据库完成聚类优化，进一步提高室内位置感知系统的定位精度和稳定性[10]。

1 基于Elman网络的VLC室内位置感知模型

1.1 Elman神经网络VLC室内定位整体综述

论文基于神经网络算法和麻雀搜索优化方法建立VLC室内位置感知模型，如图1所示。

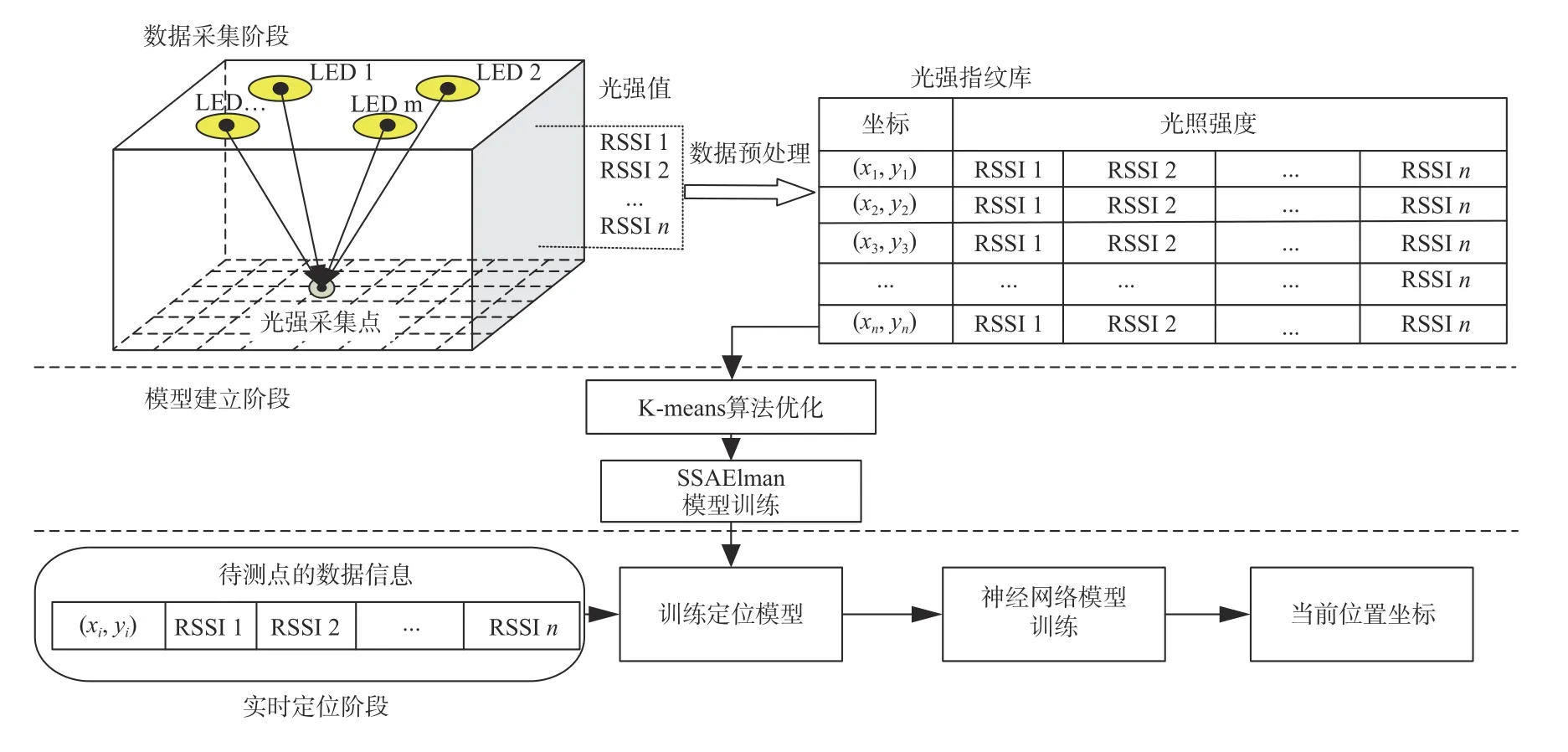
图1 定位算法整体组成图Fig.1 Overall composition diagram of positioning algorithm

数据采集阶段采集光功率，建立数据库。建模阶段利用K-means对数据库优化：随机选取 K个点为初始聚类中心；计算剩余数据与初始中心的欧式距离进行相似度评判；比较数据点与各中心点光功率的相似度形成K 个簇；反复迭代直至中心不再变化。将优化后的数据作为网络训练数据搭建Elman网络模型，利用SSA优化网络最优权阈值，建立SSA-Elman模型。实时定位阶段根据待测点信息通过模型得初步预测，将初步预测值代入子类二次训练得到预测点的最终坐标。

1.2 基于Elman神经网络的定位算法

Elman网络是对人脑基本特性的模拟和抽象中提出的一种递归神经网络[11]，如图2所示，共4层：输入层、输出层、隐含层和承接层。Elman网络无需考虑外部因素，可任意精度逼近非线性系统[12]。

图2 Elman神经网络结构图Fig.2 Structure diagram of Elman neural network

Elman神经网络数学模型为

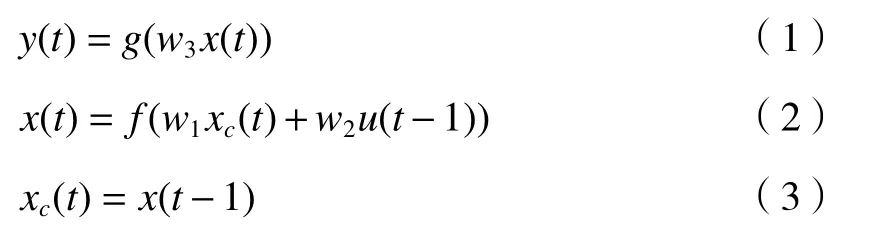
式(1)中：u(t-1)为 输入层的输入； y(t)为输出层的输出； x(t)为 隐含层输出； w1为输入层与隐含层间的连接权值； w2为 承接层与隐含层间的权值； w3为隐含层与输出层间的权值； xc为承接层输出反馈向量。(2)式中：f()为隐含层传递函数，如下：

式中：g()为输出层传递函数，常用Pureline函数，可得到(5)式：

Elman最优权阈值的设置可使网络有更好的训练效果和收敛速度。虽然Elman网络在计算能力及稳定性方面优于BP网络，但由于是基于梯度下降原理，存在最优权值难确定及由此所带来的局部极小值问题，造成网络训练难达到全局最优，影响精度和稳定性。为此引入SSA算法进行优化。

2 基于SSA算法的模型优化

2.1 SSA算法的基本原理

麻雀搜索算法具有搜索范围全面、训练速度快等优点[13]。算法的核心内容是麻雀的捕食与反捕食行为，模型建立的规则如下：

麻雀种群位置初始化，如(6)式所示：

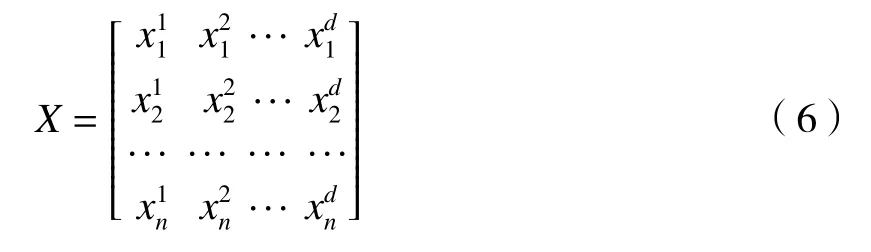
式中：d为待优化问题（神经网络初始权阈值）变量维数；n是麻雀个数。麻雀适应度为

式中：f 表示种群适应度。在SSA中，发现者的适应度值越高，越容易获取到食物。发现者位置更新如(8)式。

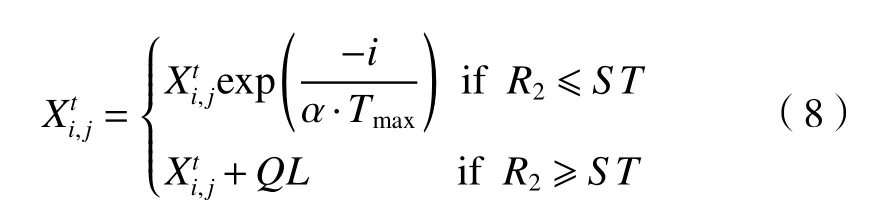
式中：t 为迭代数； Tmax为最大迭代数； α∈(0,1]是随机数； xi,j为 第i个个体在第 j维空间中的位置；R2(R2∈[0,1])为 预警值； ST(ST∈[0.5,1])为安全值；Q是随机数，服从正态分布；L表示一个1 ×d矩阵，元素全部为1。当 R2≤ST ，周围安全；当 R2≥ST，周围发现捕食者，所有麻雀飞到其他安全区域觅食。追随者位置更新如(9)式：

式中：XP和 Xw分别为目前觅食最佳和最差位置；A为 1×d 矩阵，元素为1或-1，且 A+=AT(AAT)-1。当 i≥n/2 时 ，第 i 个个体的适应度较低，要飞到其他区域觅食。当危险出现，侦察者数学表达式如下：

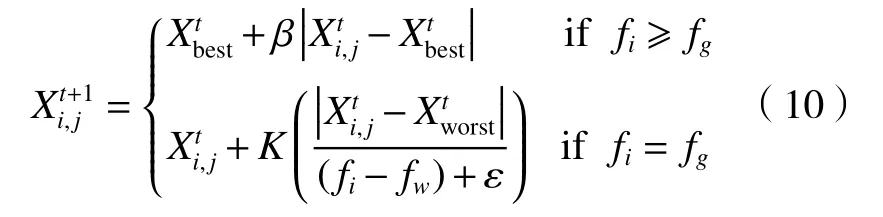
式中：fi=fg表明种群中间位置的麻雀发现危险，它们将靠近其他个体来减少自己被捕食的危险；fi≥fg表示此时麻雀在种群边缘区域，易受到外来生物的攻击； K为步长控制参数。

SSA算法有较强的全局和局部搜索寻优能力，为确保全局最优解，需保证实验数据量充足，多次寻优直至得全局最优解；同时通过目标函数优化避免收敛后期陷入局部最优。为提高效率，在精度满足时停止寻优。此时虽非全局最优解，但能满足应用需求。

2.2 基于SSA-Elman神经网络算法模型匹配算法

建立SSA-Elman网络算法模型，主要利用SSA算法搜索范围广、收敛速度快特点，对Elman网络优化，避免网络因权阈值选择不当导致精度不高的问题。算法步骤为：

1)输入数据，对获取到的训练数据和测试数据作归一化处理；

2)选择合适的参数，确定Elman网络拓扑结构、各层的节点个数及隐含层的层数；

3)构建网络模型 初始化Elman网络的权阈值，设置种群最大迭代数maxgen、种群规模sizepop等参数。定义空间维度K，如(11)式：

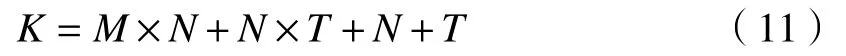
式中：M 、 N、 P分别表示输入层、隐含层和输出层神经元个数，隐含层神经元个数计算公式N≤其中 a 为1～10之间常数。

4)计算初始个体适应度，开始循环，利用SSA计算种群适应度，更新最优个体值，进行觅食与反捕食行为；进行最优个体比较，更新迄今最优个体；

5)循环步骤4)直至最大迭代次数，判断是否得到最优解，跳出循环；

6)将步骤5)中得到的权阈值作为网络参数，进行训练，构建SSA-Elman网络模型。

3 利用K-means优化SSA-Elman网络模型

利用K-means对SSA-Elman算法优化是将数据库分成 K个子类，这里的子类表示数据库经Kmeans优化过后分成的子数据库。首先对数据初步预测得到待测点类别，然后将预测类别代入子类进行二次训练预测。采用MSE(minimum squared error)[14]评价聚类效果：

通过 E相似度对子聚类对象平均值测算。k值的确定采用轮廓系数法，计算过程如下：对数据库数据聚类优化得到 k个簇并确定每个簇的中心，分别对每个簇中每个样本点i计算轮廓系数，如下：

式中：a(i)为 样本点i到同一簇中其他样本点的距离平均值，a(i)越 小该类可能性越大； b(i)为 样本点i到其他簇样本点距离平均值。s∈[-1,1]，越接近1，聚类效果越好。经对比发现本设计 k=5聚类效果最优。K-means对SSA-Elman网络模型优化流程如下：

1)在数据库随机选 K个点作为初始聚类中心点，这里 K值取5；

2)将数据库剩余数据分配到最近的数据中心形成 K 个簇，计算 K个簇聚类中心；

3)重复第2)步直至聚类中心不再变化，形成K个子集，完成数据集优化；

4)处理后数据作为SSA-Elman网络输入，输出预测数据在 K个子集中的类别；

5)将测试集数据根据类别带入所属子类中，构建 K个子SSA-Elman网络模型；

6)对K个子模型分别进行训练，得到预测点的最终坐标，计算预测坐标与真实坐标之间的误差，评判模型预测效果。

4 实验与结果分析

4.1 实验环境及参数设置

实验环境为0.8 m×0.8 m×0.8 m的立体空间，其三维示意图如图3所示。

图3 实验环境三维图Fig.3 Three-dimensional diagram of experimental environment

根据光照度补偿原理布设4个LED光源。将实验区域划分网格，在每个网格点利用光电探测仪采集来自4个不同光源的光功率值，对各光源分别采集50次数据，对采集数据处理去极值后取平均，作为该点4组光强数据。实验环境参数如表1所示。

表1 实验环境参数Table 1 Parameters of experimental environment

随机选取其中30组数据做测试数据，剩余数据做训练数据，对训练数据经聚类优化后进行实验仿真，经过SSA-Elman网络模型训练输出预测坐标。

4.2 基于K-means聚类数据库的优化

利用K-means对数据库优化，聚类个数为5，随机选取初始聚类中心开始优化，不断迭代最终聚类结果如图4所示。

图4 聚类结果Fig.4 Diagram of clustering results

由图4，经K-means聚类优化后，数据分成5类，用不同形状标签表示各类数据，各类聚类中心用实心圆标出。

4.3 基于SSA的网络训练

Elman网络训练次数设为1 000，学习速率0.01，输入层节点数4，输出层节点数2，隐含层节点通过对比平均误差设为14。SSA算法参数设置为：种群数为20，迭代次数30，种群预警值为0.7，意识到危险麻雀比重0.15，发现者比重0.8。分别利用粒子群算法和麻雀搜索算法对初始网络权阈值进行训练寻优，得到收敛曲线如图5所示。

图5中，纵坐标的适应度值为均方误差值。可以看出，随着迭代次数的增加，最佳适应度值不断下降。其中SSA在迭代次数到达8次最终稳定，而PSO迭代20次趋于稳定，且SSA确定最佳适应度值接近 2.64×10-3，PSO为 3.93×10-3，验证相较于PSO，经SSA优化后网络权阈值迭代寻优过程较快，效果更好。

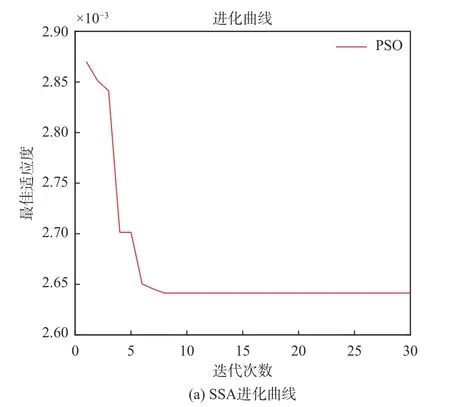
图5 神经网络训练收敛曲线Fig.5 Convergence curves of neural network training

4.4 定位数据获取及分析

数据库随机选取30组位置数据作为测试数据，得到定位误差分布图如图6所示。

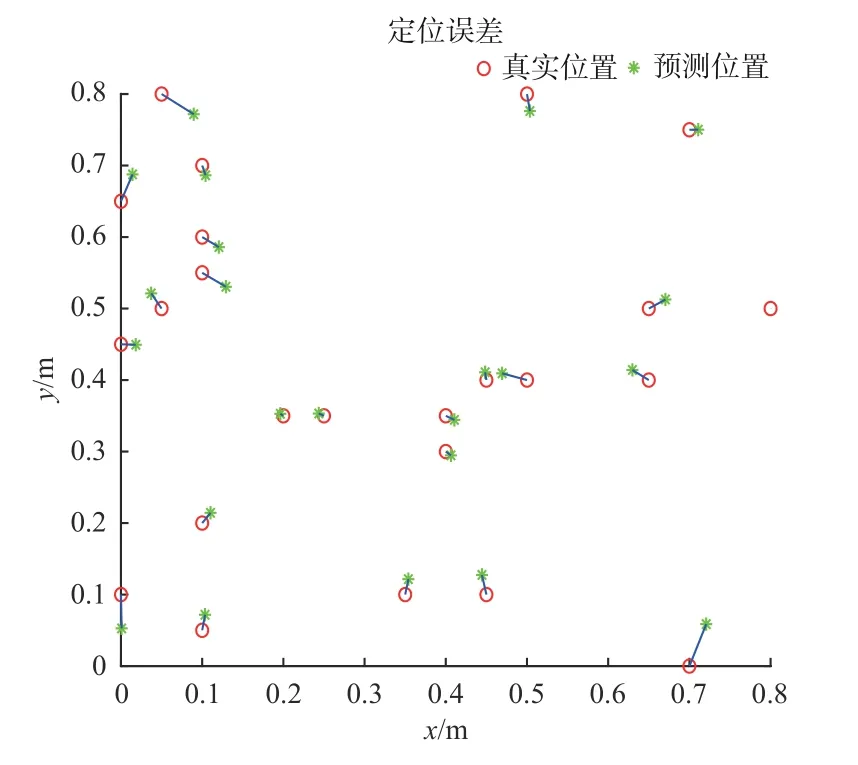
图6 定位误差分布图Fig.6 Distribution diagram of positioning error

选取其中10组位置数据，对真实坐标与预测坐标进行比较，如表2所示。

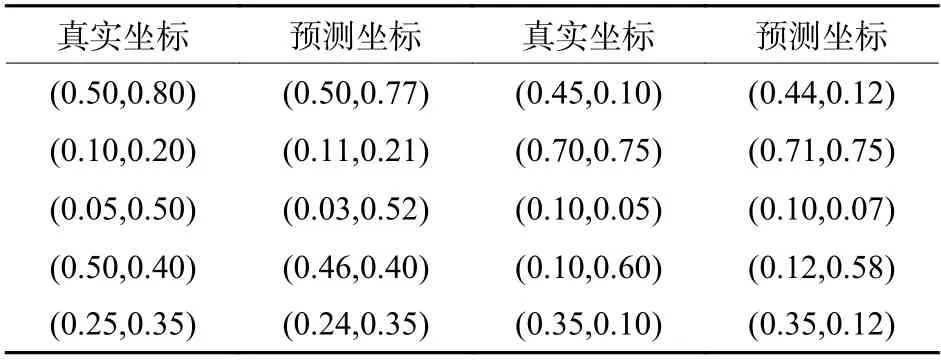
表2 位置坐标比较Table 2 Comparison of position coordinates

由图6及表2可知，大部分预测点与真实点位置接近，少部分预测点与真实点位置稍有偏差。位于实验中心区域预测点与真实点误差较小，位于实验区域四周误差偏大，原因是靠近四周，受环境影响较大，光照强度降低，定位误差增大。

将SSA-Elman网络算法、Elman网络算法及K-means+SSA-Elman算法进行比较，得累积误差分布如图7所示。

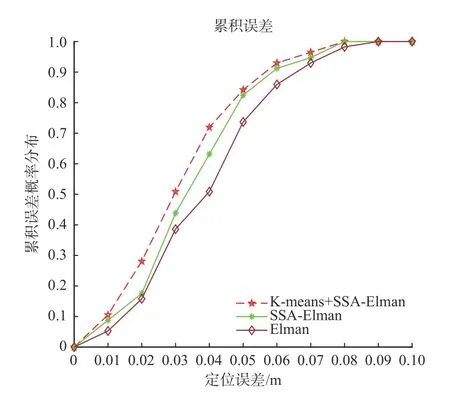
图7 累计误差分布曲线Fig.7 Distribution curves of cumulative error

由图7可知，论文算法相较SSA-Elman算法和Elman网络算法定位置信概率有明显提升，定位精度显著提高。论文算法总体定位误差分布在8 cm以内，小于6 cm的概率达到90%，相较Elman定位算法，定位误差小于2 cm置信概率提高15%，小于4 cm置信概率提高10%，小于6 cm置信概率提高11%，精度和稳定性明显提升。定位误差对比如表3所示。

表3 3种算法定位误差比较Table 3 Comparison of positioning errors of three algorithms cm

由表3知，K-means+SSA-Elman的最大误差、最小误差及平均误差均低于SSA-Elman算法和Elman算法。论文所提算法定位平均误差为3.22 cm，SSA-Elman算法平均定位误差为3.48 cm，Elman算法平均定位误差为3.87 cm。论文所提算法相较于SSA-Elman定位精度提高7.5%，相较于Elman提高16.8%。

5 结论

论文通过SSA对Elman网络进行优化，同时融合K-means算法，形成一种混合可见光室内位置感知算法，改善传统Elman网络定位算法初始权值阈值选择不当导致定位精度低、稳定性差的问题，提高室内定位精度。理论分析及实验结果表明：

1）利用神经网络算法大幅提高可见光室内位置感知结果的准确程度；

2）利用麻雀算法对Elman神经网络进行优化，能够避免网络陷入局部极小值，克服初始权阈值选择不当的问题，提高定位精度；

3）对SSA-Elman网络进行K-means优化，有效提高了位置感知系统对室内环境的适应性，进而提高定位精度和稳定性。