航空光电成像系统像移补偿技术研究

吴雄雄，栾亚东，王惠林，郑凤翥，王明超，马 莉，吴珧瑞

（1.西安应用光学研究所，陕西 西安 710065；2.93170部队，陕西 西安，710082；3.陕西科技大学 阿尔斯特学院，陕西 西安，710021）

引言

近年来航空光电成像系统主要采用多波段长焦反射式光学系统设计形式，具有时效性强、准确度高、侦察距离远、机动性灵活等特点，是目前获取战术情报的重要手段之一[1-4]。国外航空光电成像系统的代表性产品主要有美国全球鹰无人机上的光电侦察监视系统、Goodrich公司的DB110相机、ROI公司的CA295相机等[5-7]。国内航空光电侦察系统研究起步较晚，装备的航空光电侦察设备研发大多都是在国外研究基础上开展的。在航空光电系统的成像过程中，由于物方目标相对光学系统运动或载机机械振动等因素，使得目标像点在像平面发生移动，产生模糊及拖尾效应，导致图像质量下降严重。为获得运动目标的清晰图像，光学系统必须采用像移补偿技术来提高成像质量。

对光学系统成像进行像移补偿的本质，是要在相机曝光时间内使目标所成的像在探测器靶面稳定在同一位置。像移补偿方法主要分为2种：一种是直接反向移动探测器感光面，使目标持续稳定成像在同一探测单元上，实现稳定能量接收，从而获得目标清晰图像；另一种是加入运动补偿光学元件，比如快调反射镜（fast steering mirror，FSM），通过对光学元件的运动控制，使得图像在像平面内产生反向移动，在探测器成像积分时间内实现物、像相对稳定状态，从而完成目标清晰成像。移动探测器进行像移补偿，当感光介质移动的速度与像移的速度一致时，图像就被“冻结”，从而达到像移补偿的目的。该方法最早的应用实例是美国KA-112A 航空侦察相机上通过移动胶片来补偿前向像移[8]。光学系统内部加入运动补偿光学元件（快调反射镜），通过电机控制光学元件的指向角度，从而改变入射光线的方向，使曝光时刻景物像点与光敏介质之间保持相对静止，实现像移补偿。该方案在上世纪 80 年代初就已经被美国应用到了其 KS-146航空相机上[9]。当前国内外先进的航空相机，绝大部分都采用光学系统内部加入运动补偿光学元件（快调反射镜）进行像移补偿。随着航空光电侦察系统向远距、长焦、高分辨率方向的发展，以及新型载机的飞行速度不断提高，机载光电侦察平台的像移补偿技术已成为航空成像领域的一项关键技术。

1 探测器移动像移补偿原理

移动探测器进行像移补偿的基本原理是首先通过获取目标的运动参数，解算出目标成像的像移速度，然后控制探测器靶面，产生同步运动，使得目标所成像在探测器感光面的像移量为零。移动探测器进行像移补偿原理如图1所示，观察同一地物目标时，载机平台从位置Ⅰ（红色）运动到位置Ⅱ（蓝色），目标像对应从A点移动到B点，产生像移。相应移动探测器，可以实现像移补偿，得到运动目标的清晰图像。

图1 探测器移动像移补偿示意图Fig.1 Schematic diagram of image motion compensation for detector movement

探测器补偿移动速度Vi与载机平台运动速度V满足关系式（1）：

式中：H为载机飞行高度；f为光学系统的焦距，如图1所示。

移动探测器进行像移补偿原理简单，但是由于探测器靶面所处空间位置对成像比较敏感，故其控制精度要求高，且探测器整体部件复杂、质量大，因此通过移动探测器靶面进行像移补偿实现目标的稳定成像比较困难。

2 运动光学元件像移补偿原理

在光学系统内部加入运动补偿光学元件，目前主要采用基于快调反射镜的高精度像移补偿技术[10-12]。由于快调反射镜仅对光路产生折叠偏转作用，不影响光学成像像差，且快调反射镜体积小、质量轻，其运动控制精度较高，能够达到微弧度量级，因此光学系统内部加入快调反射镜进行像移补偿具有显著优势。通过精确控制快调反射镜的角度指向，使得在相机曝光时间内，目标能够稳定成像于靶面同一位置，从而实现目标的清晰成像。目前航空光电侦察系统大多使用运动光学元件进行像移补偿，国外先进侦察设备如美国“全球鹰”已经配备快调反射镜进行航空侦察的像移补偿和二级稳定控制[13]。除了航空光电侦察相机外，快调反射镜也广泛应用在航天成像系统中进行像移补偿[14-15]。

根据运动光学元件所处光路的光线会聚特性，像移补偿可以分为平行光路像移补偿和会聚光路像移补偿2种。

2.1 平行光路像移补偿

平行光路中像移补偿可分为两种：物方平行光路像移补偿和像方平行光路像移补偿。图2表示物方平行光路像移补偿。地物目标从位置Ⅰ运动到位置Ⅱ时，相应目标所成像从像点A移动到像点B产生像移。像移补偿光学元件从状态1（黑色）随动到状态2（蓝色），即可完成像移补偿，实现地物目标清晰成像。

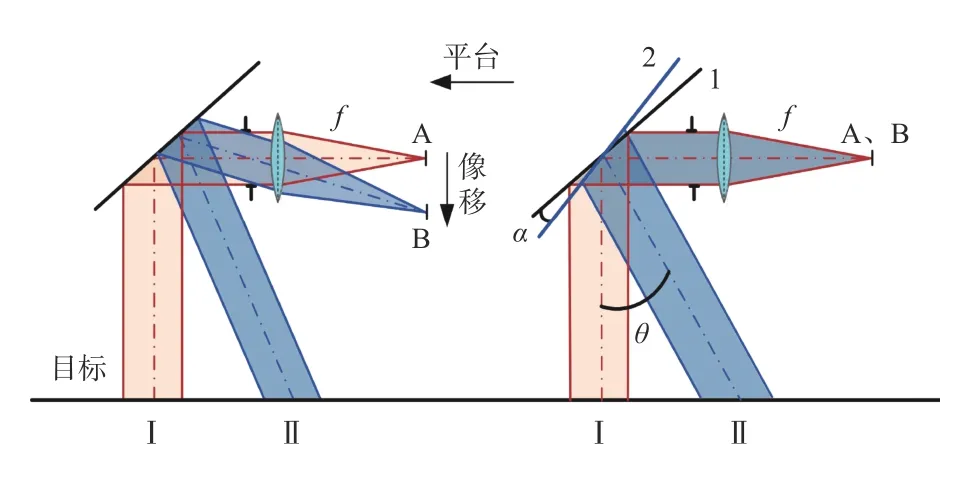
图2 物方平行光路像移补偿示意图Fig.2 Schematic diagram of image motion compensation for object side parallel optical path

像移补偿光学元件旋转角度与目标旋转角度满足关系式（2）：

式中：α为像移补偿光学元件随动角度；θ为地物目标转动角度；k为像移补偿光学元件随动系数，一般情况下默认k＝1/2。

图3为像方平行光路像移补偿示意图。地物目标从位置Ⅰ运动到位置Ⅱ时，相应目标光束经过接收望远镜后对光束口径进行压缩，放大光束角度，经过快调反射镜从状态1（黑色）随动到状态2（蓝色），完成像移补偿，最后通过中继透镜组成像到探测器焦面上B像点（与A像点重合），实现地物目标清晰成像。

图3 像方平行光路像移补偿示意图Fig.3 Schematic diagram of image motion compensation for image side parallel optical path

运动补偿光学元件旋转角度与地物目标旋转角度满足关系式（3）：

式中：α为像移补偿光学元件随动角度；k为像移补偿光学元件随动系数，k＝1/2；θ为地物目标移动角度；Γ为前端望远镜角放大倍率；β为经前端放大后地物转动角度；f1为望远物镜的焦距；f2为望远目镜焦距。当地物目标移动角度较小时，像移补偿光学元件随动角度可近似表示为（4）式：

2.2 会聚光路像移补偿

运动补偿光学元件处于像方，与处于物方相比其通光口径大幅减小。当运动补偿光学元件处于像方会聚光路中时，其通光口径可以更小。将像移补偿光学元件设置于像方会聚光路中，更有利于实现补偿控制。为了分析方便，将快调反射镜置于探测器前，经快调反射镜补偿后，运动目标成像到同一探测器单元上，实现像移补偿，如图4 所示。

图4 像方会聚光路像移补偿示意图Fig.4 Schematic diagram of image motion compensation for image side converging optical path

在上述反扫补偿光路模型中，快调反射镜运动规律应满足关系式（5）：

式中：α为像移补偿光学元件随动角度；k为像移补偿光学元件随动系数，k=1/2；θ为地物目标转动角度； Γ′为前端等效角放大倍率；β为经前端光学组件放大后地物转动角度。当地物目标移动角度较小时，像移补偿光学元件随动角度可近似表示为（6）式：

3 像移补偿像差分析

快调反射镜置于平行光路中时，像移补偿不会引起额外像差，但是当光学系统放大倍率较大时，快调反射镜的通光口径要求急剧增大，需要大口径的快调反射镜才能实现，且不利于运动控制。当快调反射镜置于汇聚光路中，尽管会产生像差，但是当光学系统放大倍率较大时，快调反射镜的通光口径变化较小，利于运动控制。快调反射镜置于汇聚光路中时，运动补偿后像面会发生倾斜，主要产生的像差为离焦像差，如图5所示，其他像差相比于离焦像差较小，不做讨论。

图5 会聚光路像移补偿离焦示意图Fig.5 Schematic diagram of image motion compensation defocus for converging optical path

运动补偿反射镜随动旋转时，实现像移补偿，但同时产生像面倾斜。像面倾斜引起的像差可以用离焦像差表示，通过Matlab数值推导，得到离焦量的数值Δh应满足关系式（7）：

式中：Δh为像面离焦量；f为前端光学系统的等效焦距；L为反射镜后截距；θ为物方入射光束角度；α为像移补偿反射镜旋转角度。

3.1 离焦对波像差影响分析

如图6所示，O为出瞳中心，F是理想成像的轴上像点，在出瞳面上的成像波面是Σ，它是以F为球心、R为半径的参考球面，即是波像差等于零的情况。现在出现离焦，即像面沿轴平移了距离Δ，达到F′点处，此时的参考球面Σ′的半径为（R+Δ）。Σ与Σ′的距离ΔW是像点F′与F的波像差。

图6 离焦量与波像差几何关系Fig.6 Geometric relationship between defocus distance and wave aberration

由几何关系可得波面Σ的矢高W可以表示为W=D2/4(2R-W)，当W相比于2R很小时，上式近似为W=D2/8R，同理离焦波面Σ′的矢高为W′=D2/8(R+Δ)。在光瞳面边缘处两波面的水平距离ΔW=W－W′=D2Δ/[8R(R+Δ)]。当离焦量Δ比较小、Δ ≪R时，ΔW=D2Δ /(8R2)。

一般情况下，波像差的单位是以波长λ为计数单位，将R替换为焦距f，得出离焦量与波像差峰峰值的关系如（8）式所示：

式中：Wpp为波像差峰峰值；F为光学系统F数；λ为工作波长；Δ为离焦量。离焦量与波像差峰峰值的关系如图7所示，可以看出随着离焦量的增加，波像差呈线性增大趋势。另外，从图中还可以看出随着光学系统F数增加，光学系统的波像差减小。

图7 离焦量与波像差关系Fig.7 Relationship between defocus distance and wave aberration

3.2 离焦对光学传递函数的影响分析

离焦光学传递函数MTFoptics可近似表示为衍射限光学传递函数MTFdiff与离焦光学传递函数MTFdefocus的乘积[16]，即MTFoptics=MTFdefocus×MTFdiff。离焦光学传递函数MTFdefocus的计算公式如（9）式所示：

衍射限光学传递函数MTFdiff计算公式如（10）式所示：

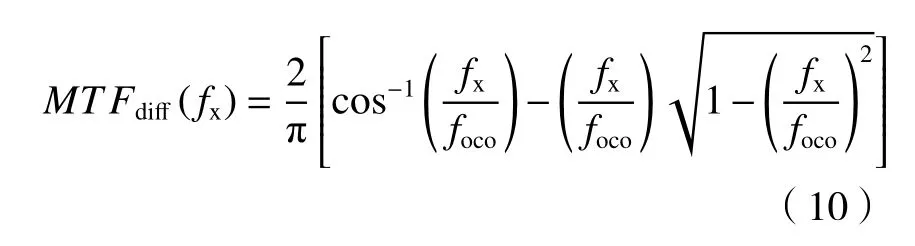
式中：fx/foco表示归一化频率；fx表示空间频率；foco=D/λ，表示光学截止频率。

航空光电成像系统一般采用长焦反射式光学系统设计形式，具有焦距长、F数大等特点。图8给出了归一化频率下F数等于8，在奈奎斯特（Nyquist）频率处（fx/foco=0.5）离焦光学系统MTFoptics与离焦量的关系曲线，可以得出，光学传递函数曲线随着离焦量的增加而降低。

图8 不同离焦量的MTF曲线Fig.8 MTF curves for different defocus distances

计算在奈奎斯特频率处（fx/foco=0.5）零离焦量基础上的MTF值下降的百分比，结果如表1所示，可以看出在奈奎斯特频率处，当离焦量在0.1 mm以内，MTF的下降量在26.6%以内。

表1 不同离焦量对应的光学调制传递函数下降值Table 1 Decreased values of optical modulation transfer function corresponding to different defocus distances

4 结论

快调反射镜以其响应速度快、定位精度高、带宽高等优点被广泛应用于航空光电像移补偿系统。本文介绍了光学系统像移补偿基本原理，包括探测器移动像移补偿与运动光学元件像移补偿，并针对基于快调反射镜的高精度像移补偿技术，通过工程简化分析，推导了快调反射镜位于平行光路像移补偿与汇聚光路像移补偿的随动角度规律，建立了汇聚光路中快调反射镜带来的离焦量理论模型，并研究了离焦量对光学系统波像差与光学传递函数的影响，研究结果可为光电成像系统像移补偿的工程应用提供理论指导。