一种求解风电机组最优轮毂高度的数学模型

袁宗涛

(北京瑞科同创能源科技有限公司，北京 100075)

0 引言

轮毂高度的选择是风电机组选型的重要环节。随着中国风电行业平价时代的到来，为了应对电价和风资源水平双降对风电行业带来的挑战，高轮毂机型将会大量出现，这对轮毂高度选择方法的科学性和严谨性提出了更高要求。

该研究假设在一定边界条件下存在最优轮毂高度，并且给出数学模型。但是受限于设备制造水平和风电机组塔架高度定制化的局限性，实际情况往往是在风电机组厂家提供的若干种塔架高度中择优选用。目前轮毂高度比选的研究偏向于案例分析，缺乏理论模型支撑，科学性和严谨性不足。主要存在如下问题：1)不能确定在可选轮毂高度之外是否存在更优轮毂高度，常规方法不能科学地掌握轮毂高度与对其选择造成影响的各因素之间的关系；2)当可选轮毂高度较多时，常规方法需要对每一种轮毂高度下风电机组的经济性进行单独测算，择优选取，导致工作量大、效率低。

本文旨在建立一种求解风电机组最优轮毂高度的数学模型，并给出具有普适性的轮毂高度比选方法。从相对轮毂高度的边际收益模型和边际成本模型的建立展开研究，边际收益模型的建立涉及功率曲线、风廓线和风速分布模型，重点在于建立风电机组年均发电量与轮毂高度之间的函数关系，在一定电价和折现率下确定相对轮毂高度的边际收益现值；边际成本模型的重点在于建立塔架质量与轮毂高度之间的函数关系，通过计算固定成本和可变成本求得相对轮毂高度的边际成本；通过模型最终得到风电机组的最优轮毂高度。基于最优轮毂高度给出3种最佳轮毂高度比选方法，提高了轮毂高度比选方法的科学性和严谨性。

1 模型概述

轮毂高度的比选实质上是风电机组经济性的比选，最优轮毂高度即风电机组收益最大化时对应的轮毂高度。一般情况下，风电机组的总收益会随着轮毂高度的提升而增加，但同时其建设成本也会增加。

本文假设存在某个轮毂高度，使风电机组的净收益最大，此轮毂高度即为最优轮毂高度，即式(1)有解。

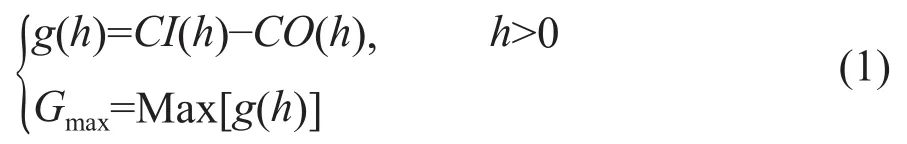
式中：h为风电机组的轮毂高度，m；g(h)为关于轮毂高度的风电机组的净收益函数；CI(h)为现金流入，表示关于轮毂高度的风电机组总收益函数；CO(h)为现金流出，表示关于轮毂高度的风电机组总支出或总成本函数；Gmax为风电机组的最大净收益，万元。

进一步将问题转化为求解式(2)：

式中：g(h)′为g(h)的一阶导数。

即：

式中：CI(h)′为CI(h)的导数，表示相对轮毂高度的边际收益；CO(h)′为CO(h)的导数，表示相对轮毂高度的边际成本。

2 相对轮毂高度的边际收益

风电机组总收益CI的计算式为：

式中：ω为风电机组发电量折减系数，取值通常介于0.7～0.8之间，为无量纲常数；Eout为风电机组年均理论发电量，kWh；pe为售电电价，元/kWh；i为折现率，%；n为折现年数或风电机组运行年数。

关于风速v的风电机组年均理论发电量函数Eout(v)的计算式为：

式中：T为一年的小时数，h，取值为8760；vci为切入风速，m/s；vco为切出风速，m/s；vr为额定风速，m/s；Pf(v)为风速介于切入风速和额定风速之间时风电机组的功率曲线函数；f(v)为风速的密度分布函数；P(v)为不同风速段下风电机组的输出功率函数；Pr为风电机组的额定功率，kW。

为确定风电机组总收益与轮毂高度之间的关系，需要把式(5)的积分结果转化为关于轮毂高度的函数，即：

结合式(4)、式(6)，即可得到风电机组边际收益与轮毂高度的函数关系，即：

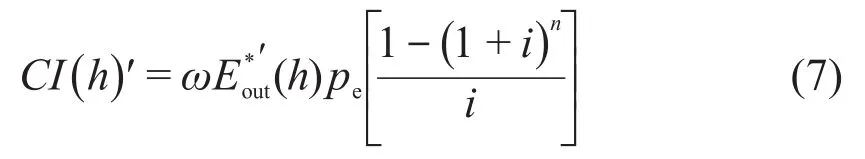
2.1 功率曲线

风电机组的输出功率特征通常用功率曲线来表示，其在不同风速段的输出功率特征如式(8)所示[1-2]：

当风速小于切入风速时，风电机组不启动，此时其输出功率为零；在风速介于额定风速和切出风速之间时，风电机组按照额定功率满功率运行；当风速大于切出风速时，风电机组停机，此时其输出功率为零；在风速介于切入风速和额定风速之间时，功率曲线主要取决于风电机组的功率控制，此时功率曲线的表现要比其他风速段都要复杂，此风速段的风电机组功率曲线也是数学模型的核心所在。

风速介于切入风速和额定风速之间时的风电机组功率曲线数学模型有多种，文献[1-3]都对此类数学模型进行过研究，但是由于其复杂性，导致这些研究的结论并不完全一致。文献[2]将9种数学模型应用到32台商用风电机组的功率曲线分析，并进行对比研究，研究后发现，基于功率因数的模型(power cofficient model)和通用数学模型(general model)的相对误差最小。本研究认为，相比于其他研究，文献[2]的研究样本更多，论证相对更充分，适用性更广，因此本文采用通用数学模型来模拟风速介于切入风速和额定风速之间时风电机组的功率曲线。该通用数学模型可表示为：

式中：k为功率曲线的幂次，本文取值为1.2。

以某单机容量为3000 kW、叶轮直径为155 m的风电机组(下文简写为“155-3000风电机组”)为例，采用通用数学模型模拟的风电机组功率曲线(k=1.2，Pr=3000)及理论功率曲线如图1所示。

图1 某155-3000风电机组的理论功率曲线及模拟功率曲线Fig. 1 Theoretical power curve and simulated power curve of a 155-3000 wind turbine

2.2 风廓线

在风资源评估中，风廓线用来描述风速随高度的变化规律。应用比较广泛的风廓线模型有幂律风廓线模型和对数风廓线模型，本文采用幂律风廓线模型。该模型可表示为：

式中：Vave为年均风速，m/s；α为切变指数，为无量纲；β为常数。

本文后续案例分析中探讨了在轮毂高度风速一定的前提下，切变指数对轮毂高度选择的影响，则式(10)可变形为：

式中：Vhub为轮毂高度的年均风速，m/s；z为距离地表的高度，m。

2.3 风速分布

风速的密度分布函数通常采用双参数的威布尔分布，为简化数学模型，本文采用形状参数q=2时的威布尔分布，即瑞利分布，可表示为：

式中：σ为尺度参数，m/s；e为自然常数。

根据瑞利分布密度函数，尺度参数和年均风速的关系可表示为：

不同年均风速下的瑞利分布如图2所示。

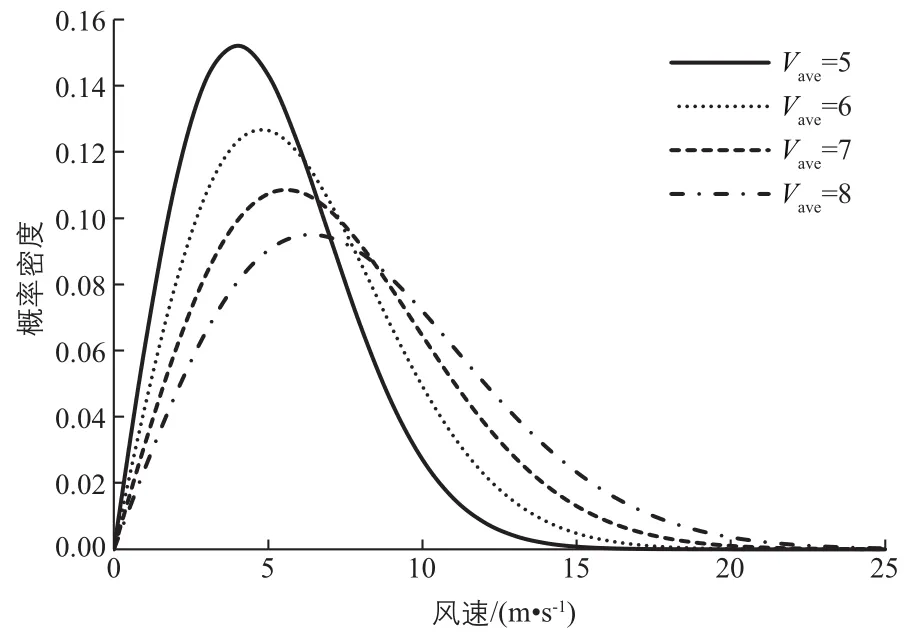
图2 不同年均风速下的瑞利分布Fig. 2 Rayleigh distribution under different annual average wind speeds

结合风廓线模型，可将轮毂高度作为参数引入瑞利分布密度函数，进而引入收益模型。根据式(12)、式(13)可得：

3 相对轮毂高度的边际成本

风电机组的总成本由固定成本和可变成本构成。其中，固定成本不随风电机组轮毂高度的变化而变化，是由风电机组的装机容量和单位千瓦造价相乘得出；本文提出的风电机组最优轮毂高度数学模型重点关注可变成本部分。

风电机组的总成本模型可表示为：

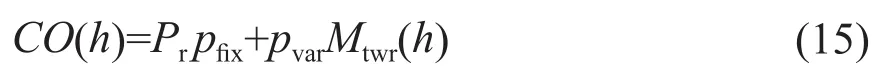
式中：pfix为风电机组的单位千瓦造价，元/kW；pvar为风电机组单位高度塔筒的造价，元/m；Mtwr(h)为关于轮毂高度的塔筒质量函数，kg。

塔筒形式与结构多种多样[4-5]，本研究基于应用最为广泛的钢制锥形塔筒进行研究设计。由于该种形式的塔筒主要是按质量计价，在单价固定的前提下，关键是确定塔筒质量和其高度之间的关系。但是，即便是锥形塔筒，其设计形式也不一而足[5-6]，直接建立数学模型会比较困难。因此为简化模型，本研究选取了42种当下主流的风电机组机型及其塔筒作为样本，选用5种模型对这42种主流机型轮毂高度与塔筒质量之间的关系进行拟合，然后择优选取。

这5种模型分别是：二次多项式模型、三次多项式模型、对数模型、幂律模型和指数模型。采用不同模型时轮毂高度-塔筒质量的拟合函数如式(16)～式(20)所示。

二次多项式模型的拟合函数为：

式中：c1、c2均为系数。

三次多项式模型的拟合函数为：

式中：c3为系数。

对数模型的拟合函数为：

幂律模型的拟合函数为：

指数模型的拟合函数为：

5种模型得到的轮毂高度-塔筒质量拟合函数的参数估计值如表1所示，拟合曲线图形如图3所示。

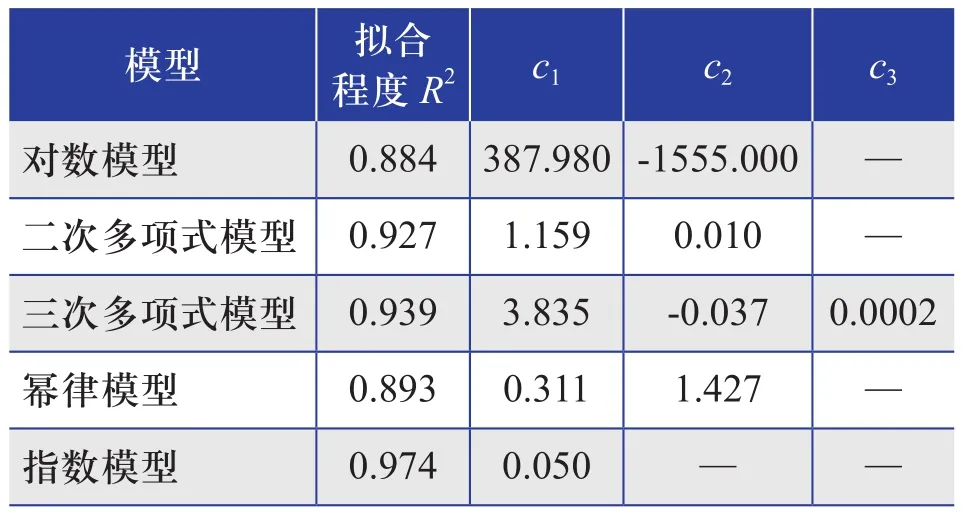
表1 5种轮毂高度-塔筒质量拟合函数的参数估计值Table 1 Parameter estimation of five fitting functions of hub heights-tower mass

图3 5种轮毂高度-塔筒质量的拟合曲线对比Fig. 3 Comparison of five fitting curves of hub heights-tower mass

从拟合优度、预测准确度和模型简洁性3个方面进行综合考虑后，本文采用二次多项式模型。由式(15)、式(16)可得到风电机组的边际成本CO(h)′与风电机组轮毂高度的函数关系，即：

4 最优轮毂高度及最佳轮毂高度比选方法

当风电机组的边际收益等于边际成本时，此时项目的净收益最大，可求得风电机组的最优轮毂高度h0。即，当h=h0时，下式成立：

需要注意的是，此时得到的最优轮毂高度为理论计算值。在实际工程应用中，通常是在风电机组出厂标配的有限的若干种轮毂高度中择优选取，作为最佳轮毂高度hbt。下文提出3种轮毂高度比选方法，所得轮毂高度即为最佳轮毂高度(即相对最优)；最佳轮毂高度可以与最优轮毂高度相同，也可以不相同。

假设某种风电机组机型的可选轮毂高度为ht(t=1, 2, 3, …,m)，且ht+1＞ht，可通过直接计算法、判别法、快速近似判别法3种算法解得风电机组最佳轮毂高度。

1)直接计算法。通过Max[g(ht)]得到的轮毂高度即为最佳轮毂高度，但此方法需要对所有备选轮毂高度进行逐次计算。

2)判别法。当h0≥hm时，则风电机组最佳轮毂高度为hm；当h0≤h1时，则风电机组最佳轮毂高度为h1；当h1≤hj≤h0≤hj+1≤hm(j为紧邻h0的那个高度的编号)时，则风电机组最佳轮毂高度为hj或hj+1，此时可转为直接计算法或快速近似判别法求解。

3)快速近似判别法。此方法假定g(h)在可行域内以h=h0为轴对称，则Min|ht-h0|对应的轮毂高度即为最佳轮毂高度。此方法可描述为“距离最优轮毂高度最近者为最佳”。

当可选轮毂高度的最大值小于等于最优轮毂高度时，最大值为最佳轮毂高度；当可选轮毂高度的最小值大于等于最优轮毂高度时，最小值为最佳轮毂高度。若可选最佳轮毂高度大于最优轮毂高度，则必定存在1个小于最优轮毂高度且收益相同的高度， 可近似为最优轮毂高度的对称高度(即2h0-hbt)。

5 算例

假设某风电场140 m高度的年均风速为6 m/s，服从瑞利分布，切变指数为0.14；选用某厂家制造的155-3000风电机组机型，按照前文所述方法计算该风电机组的最优轮毂高度，同时在给定的几种风电机组轮毂高度中选择最佳轮毂高度。计算时各参数取值如表2所示。

表2 计算中的参数取值Table 2 Parameter value in calculation

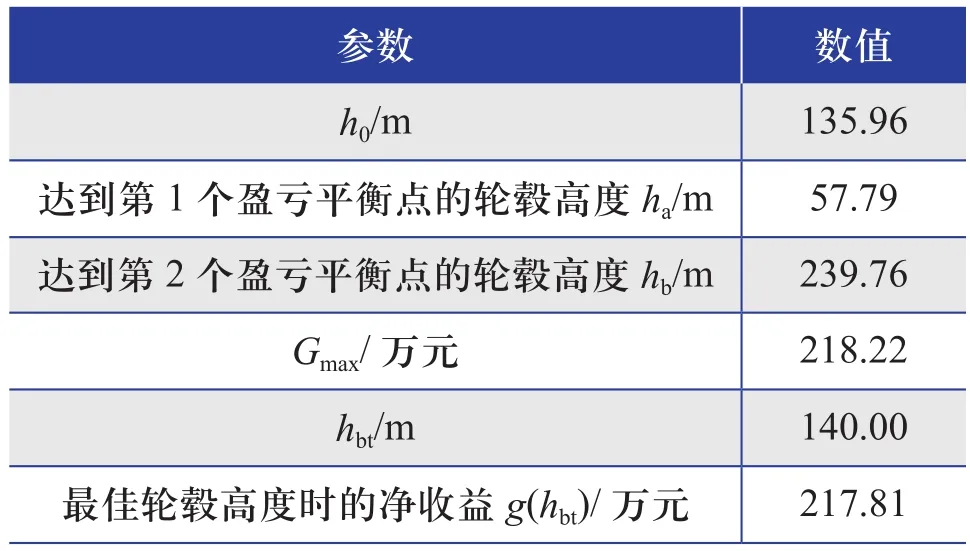
表3 计算结果Table 3 Calculation results

风电场达到第1个盈亏平衡点和第2个盈亏平衡点时，其总收益与总成本相等。风电场的总收益和总成本与风电机组轮毂高度的关系曲线如图4所示。

图4 风电场的总收益、总成本与轮毂高度的关系曲线Fig. 4 Relationship curve between total revenue and total cost of wind farm and hub height

最优轮毂高度时风电场的净收益最大。风电场的净收益与风电机组轮毂高度的关系曲线如图5所示。

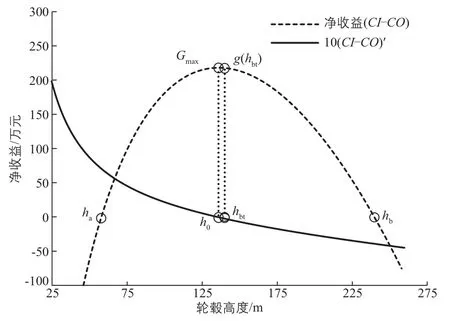
图5 风电场的净收益与轮毂高度的关系曲线Fig. 5 Relationship curve between net income of wind farm and hub height

不同切变指数取值下的最优轮毂高度的变化情况如图6所示，不同塔筒单位造价下的最优轮毂高度的变化情况如图7所示。

图6 不同切变指数取值下的最优轮毂高度的变化情况Fig. 6 Variation of optimal hub height under different shear index values

图7 不同塔筒单位造价下的最优轮毂高度的变化情况Fig. 7 Variation of optimal hub height under different unit cost of tower

由图6可以看出：曲线上边际净收益为零时对应的轮毂高度即为最优轮毂高度，随着切变指数取值的增大，最优轮毂高度也在增加。

由图7可以看出：曲线上边际净收益为零时对应的轮毂高度即为最优轮毂高度，随着塔筒单位造价的提高，最优轮毂高度逐渐减小。

6 结论

本文建立了一种求解风电机组最优轮毂高度的数学模型，并给出了具有普适性的轮毂高度比选方法。通过建立模型，确定输入参数，经过算例验证，得到以下结论：

1)在可行域内，风电机组存在最优轮毂高度且值为唯一。

2)当可选轮毂高度的最大值小于等于最优轮毂高度时，最大值为最佳轮毂高度；当可选轮毂高度最小值大于等于最优轮毂高度时，最小值为最佳轮毂高度。若可选最佳轮毂高度大于最优轮毂高度，则必定存在1个小于最优轮毂高度且收益相同的高度。即若最佳轮毂高度大于最优轮毂高度，在获得同等收益的前提下其必定可以优化，以减少资源浪费。

3)最优轮毂高度与切变指数成正比，与塔筒单位造价成反比，与风电机组的固定成本无关。