压浪板对高速两栖平台运动稳定性影响的数值分析

2022-07-05杜尊峰慕旭亮李志军

中国舰船研究 2022年3期

杜尊峰，慕旭亮，李志军

1 天津大学建筑工程学院水利工程仿真与安全国家重点实验室，天津 300354

2 铁鹰特种车（天津）有限公司，天津 300232

0 引言

两栖平台作为一种高效的水陆交通工具，能够承担野外侦察、物资运输、水上巡逻以及抢滩登陆等多种任务，并开始朝着高速以及超高速的方向发展[1]。为了提高两栖平台的水上性能，余祖耀等[2-4]从滑板角度、车轮抬升等因素出发优化外部型线，并考虑航行环境因素对平台性能的影响，为其在各航行状态下的性能提高提供了可靠依据，但所针对的目标多为中、低速排水型平台，缺乏对于高速平台的关注。凌宏杰等[5-6]对高速滑行艇的运动进行了研究，结果显示在高速状态下，艇体会出现“海豚运动”现象，并且随着航速的增加，其升沉量、纵倾角以及响应频率也会随之增大，对航行稳定性影响较大。与高速艇相比，水陆两栖平台的结构长宽比更小，除却在外形减阻方面的研究，其高速航行时的姿态及其稳定性更加不能忽视。

压浪板与阻流板等附体装置作为滑行艇以及其他高性能船舶常用的增效装置，能够降低纵摇以及升沉幅值，可见适宜的安装能够改善船舶航行姿态[7-9]。同时，也有研究表明，翼板辅助装置能够显著改善中、低速阶段两栖平台的航行性能与姿态[10]。然而，针对压浪板的研究很少涉及高速两栖平台，因此，有必要结合压浪板来分析两栖平台在高速航行阶段的水动力特性。

近年来，CFD 数值模拟技术的发展为舰船与水上平台的性能研究提供了较好的技术支撑[11-12]。本文将以某两栖平台为研究对象，探讨在高速航行阶段压浪板对其的影响。首先，采用CFD 数值方法对高速航行状态下的平台进行模拟计算，分析压浪板的水动力作用机理，进而研究其对平台纵向运动姿态，即动态响应的影响特性，然后基于计算结果和支持向量机（support vector machine，SVM）分类方法，找寻平台在不同工况下的运动稳定性边界，为高速两栖平台的性能改善提供参考。

1 数值方法及验证

1.1 数值计算方法

在笛卡尔坐标系下，绕平台流动的不可压缩流体所满足的连续性与动量守恒控制方程如下：

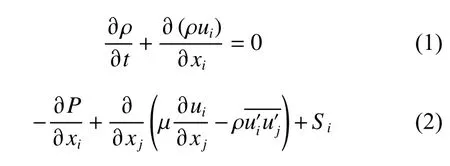
采用有限体积法（finite volume method，FVM）对流动控制方程进行离散，并通过网格划分形成互不交叉的控制单元，整个场域的质量与动量守恒分解为每个控制单元上的有限积分[13]，对流项使用二阶迎风插值格式，扩散项的离散采用中心差分格式，并采用SIMPLE 分离式算法进行求解。

引入剪切应力传输SSTk-ω 两方程湍流模型，以使控制方程封闭可解。该模型使用了一个混合函数，在边界层内部采用k-ω 模型，外部使用k-ε 模型，控制方程中包含有远离壁面的交叉扩散项。

使用基于欧拉多相流的流体体积（volume of fluid，VOF）法对自由液面进行捕捉，即当单元内充满液相流体时，其体积分数Cq=1，当单元内充满气相流体时，Cq=0，通过计算各单元中液相流体的体积分数来确定自由液面的近似位置[14]。其连续性方程为：

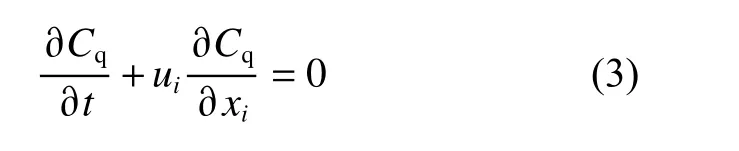
将计算区域划分为背景域和重叠区域，其中背景区域静止，重叠区域伴随船体的运动。两个区域的网格单独生成，避免了整个流域内的网格随船体运动而产生变形，背景区域与重叠区域在交界处的网格尺度保持同等水平以减小数值误差，并通过线性插值方式进行两套网格之间的信息传递。船体的纵向运动为二自由度，包含纵摇与升沉，根据质心运动及绕质心的动量矩定理，其运动方程为：

1.2 数值计算验证

为了保证数值计算的可靠性，基于GPPH （generic prismatic planing hull）滑行艇的试验结果，对数值计算方法进行了验证，并将计算结果与试验及文献[15-16]中的数据进行了对比。图1 所示为GPPH滑行艇的型线图，表1 所示为该艇的主尺度及相关参数。

图1 GPPH 滑行艇外形Fig. 1 Outline of GPPH planing craft

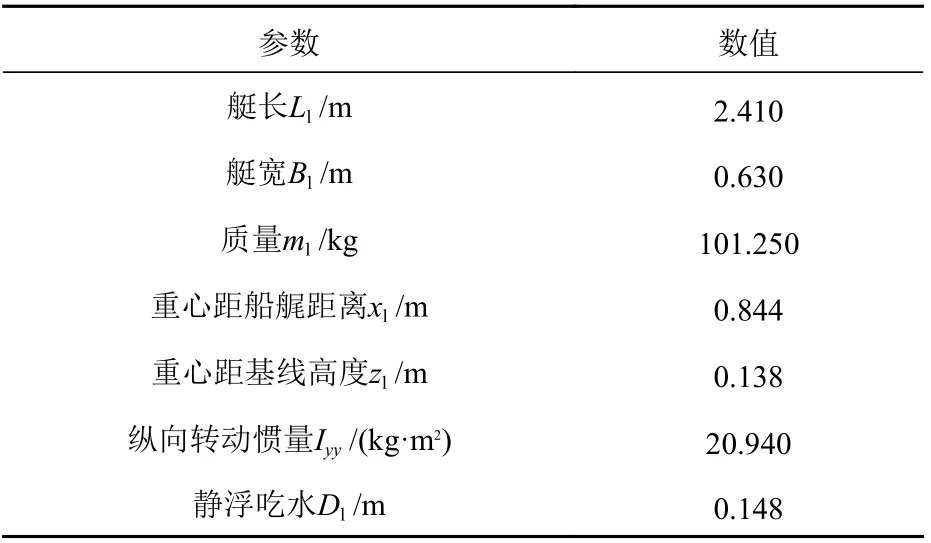
表1 GPPH 滑行艇结构参数Table 1 Parameters of GPPH planing craft

重叠区域与背景区域的网格划分结构如图2所示，其中背景区域大小为5L1×2L1×2L1，重叠区域大小为1.5L1×0.4L1×0.4L1。对重叠网格外围区域适当加密，以保证背景区域与重叠区域网格之间合理过渡，同时对水线面与艇体尾部开尔文兴波区域的网格也进行相应的细化处理。根据船舶CFD 的计算经验，艇体表面的网格尺寸取艇长的8‰，壁面y+值取为50，表面边界层数为6，增长率为1.3。

图2 网格与边界设置Fig. 2 Grid and boundary setting

根据来流的位置与方向，将艇体的上、下边界与前端边界均设置为速度入口，尾部边界压力设为出口边界，左、右边界根据运动计算的对称性设置为对称平面，并在压力出口区域施加VOF 波阻尼，以减弱出口处因数值反射造成的回流影响。

由图3 所示GPPH 滑行艇的数值计算结果，发现纵倾角、龙骨线湿长度的结果与试验及文献[16]中结果具有相同的变化特点，并且误差较小，即采用上述数值计算方法对高速航行状态下的船舶进行数值模拟，能够得到较为准确的运动响应结果。

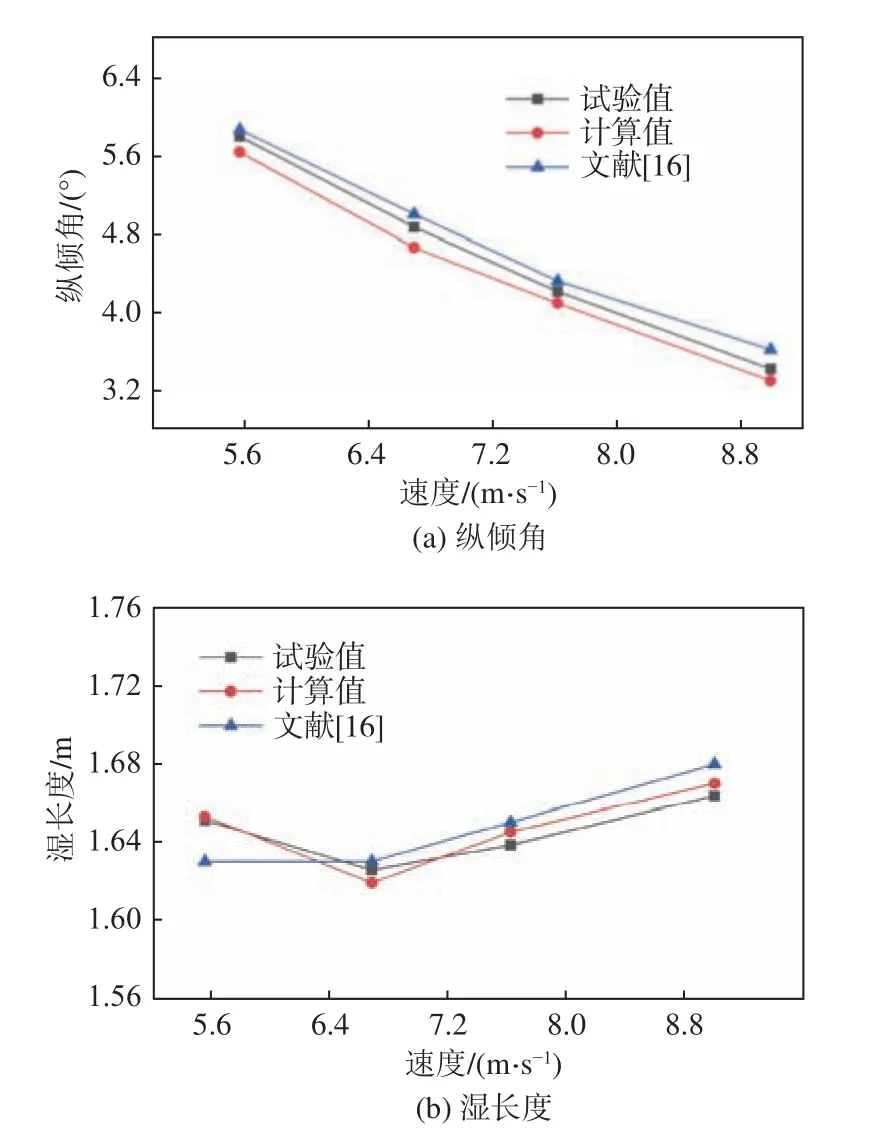
图3 数值方法验证结果Fig. 3 Verification results of numerical method

2 两栖平台高速运动分析

本文研究对象为某高速滑行型两栖平台，其在v= 20～25 kn 高速工况下的体积弗劳德数Fr∆≈ 3.0，因航行状态与高速艇类似，故沿用上述GPPH 滑行艇采用的数值方法进行实尺度平台在高速运动状态下的数值计算，计算区域大小和网格尺度以两栖平台总长L为基准进行确定。表2 所示为平台主尺度信息，图4 所示该平台的外形与艉部压浪板结构示意图，其中压浪板分布在平台中纵剖面两侧，其下旋角度用α（单位：(°) ）表示。

图4 两栖平台外形与艉压浪板示意图Fig. 4 Outline of amphibiou platform and stern flap

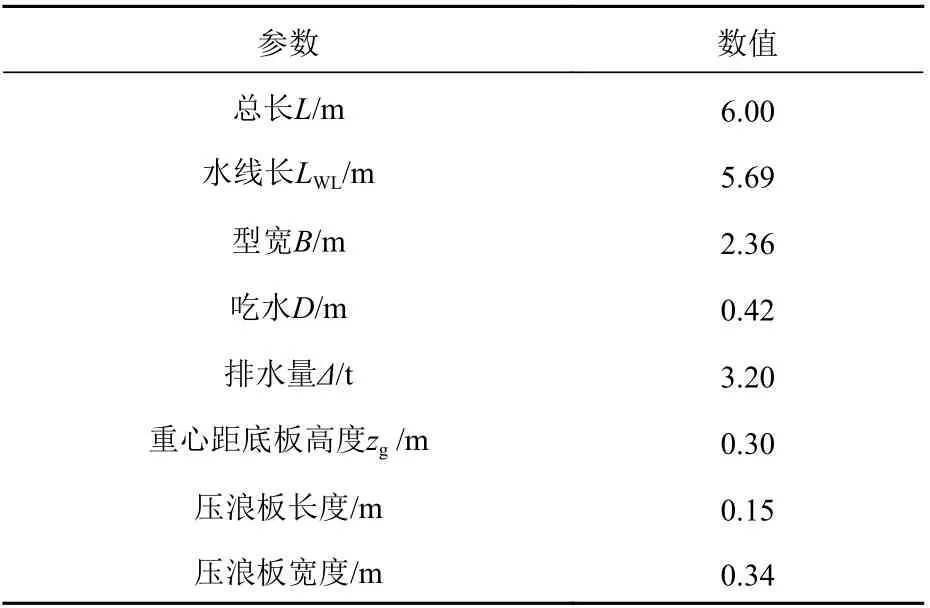
表2 两栖平台参数Table 2 Parameters of amphibious platform

基于上述数值方法，对两栖平台的表面网格进行敏感性分析。计算中，平台表面将分别以14，20，28 mm 这3 种细、中、粗网格予以划分，网格尺度分别为平台总长的0.23%，0.33%和0.46%。按照前述计算域内网格细化方法，这3 种方案的网格数分别为1.15×107，5.03×106和2.33×106。

本研究的重点在于分析压浪板对两栖平台纵向运动的影响，故选取α= 8°，23°这2 种角度的压浪板进行验证，验证航速为22 kn。在3 种网格情况下计算得到的平台航行姿态结果如表3 所示。从中可以看出，不同网格水平下纵倾角与升沉结果间差别较小，且随着网格尺度逐渐细化，平台姿态间的差异随之减小，具有收敛的趋势。综合考虑计算效率与精度，确定平台表面的网格尺寸为 20 mm，压浪板表面网格细化为5 mm。基于流场是关于平台中纵剖面对称的考虑，将以半侧流场进行数值计算，压浪板处的网格划分如图5 所示。

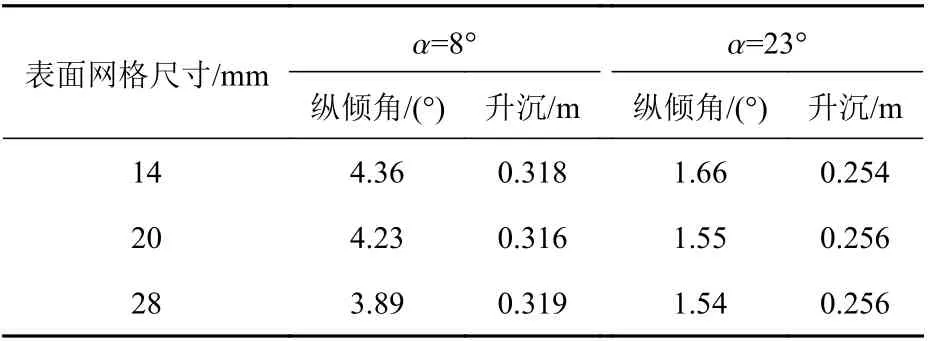
表3 网格敏感性结果Table 3 Results of grid sensitivity

图5 压浪板网格划分Fig. 5 Grid division of stern flap

2.1 压浪板水动力性能分析

2.1.1 对纵向运动的影响

为定性分析压浪板对高速两栖平台水动力性能的影响，对平台在不同下旋角压浪板作用下的运动特性进行计算。表4 所示为相应的纵倾角与相对升沉结果，其速度工况为v= 22 kn，重心在纵向距离艉板0.43L。

表4 22 kn 速度下的纵向运动结果Table 4 The results of longitudinal motion at a speed of 22 kn

由表4 可知，随着压浪板下旋角度α 的增加，平台纵倾角呈减小趋势，且α 愈大其纵倾角减小得越明显，同时，平台整体的升沉量也随α 的增加而减小。究其原因可能在于，因压浪板作用在平台艉部，故其对纵倾角的影响相对较大，而对平台整体的垂向抬升效果则不明显，且相反地，由于纵倾角减小的原因，升沉量也随之降低。

2.1.2 对波流场与压力场的影响

为研究压浪板对平台尾流场波形的影响，选取不同α 作用下不同纵剖面处的波形进行分析，所选纵剖面至中纵剖面的距离分别为Y=0，0.55，1.0，1.75 m，压浪板布置在平台艉部，距离中纵剖面0.55 m。图6 所示为各剖面处的波形结果，其中X为纵向位置坐标。

由图6 可知，压浪板对远场波形的影响较小，在不同下旋角压浪板作用下，远场的波形基本一致，其主要作用范围靠近压浪板本身，约处于6～12 m 的范围内；随着α 的增加，Y= 0.55 m 位置处波形在压浪板后有着较明显的下降，其“虚尾”长度则基本相同，而在压浪板两侧，Y= 0 m 和Y=1.0 m 位置处的波形则因压浪板的挤压有明显的上升；在平台宽度之外，也即Y= 1.75 m 位置处，波峰高度与波谷深度随着α 的增加而减小，可见在高速下压浪板对改善波流场具有一定的效果。

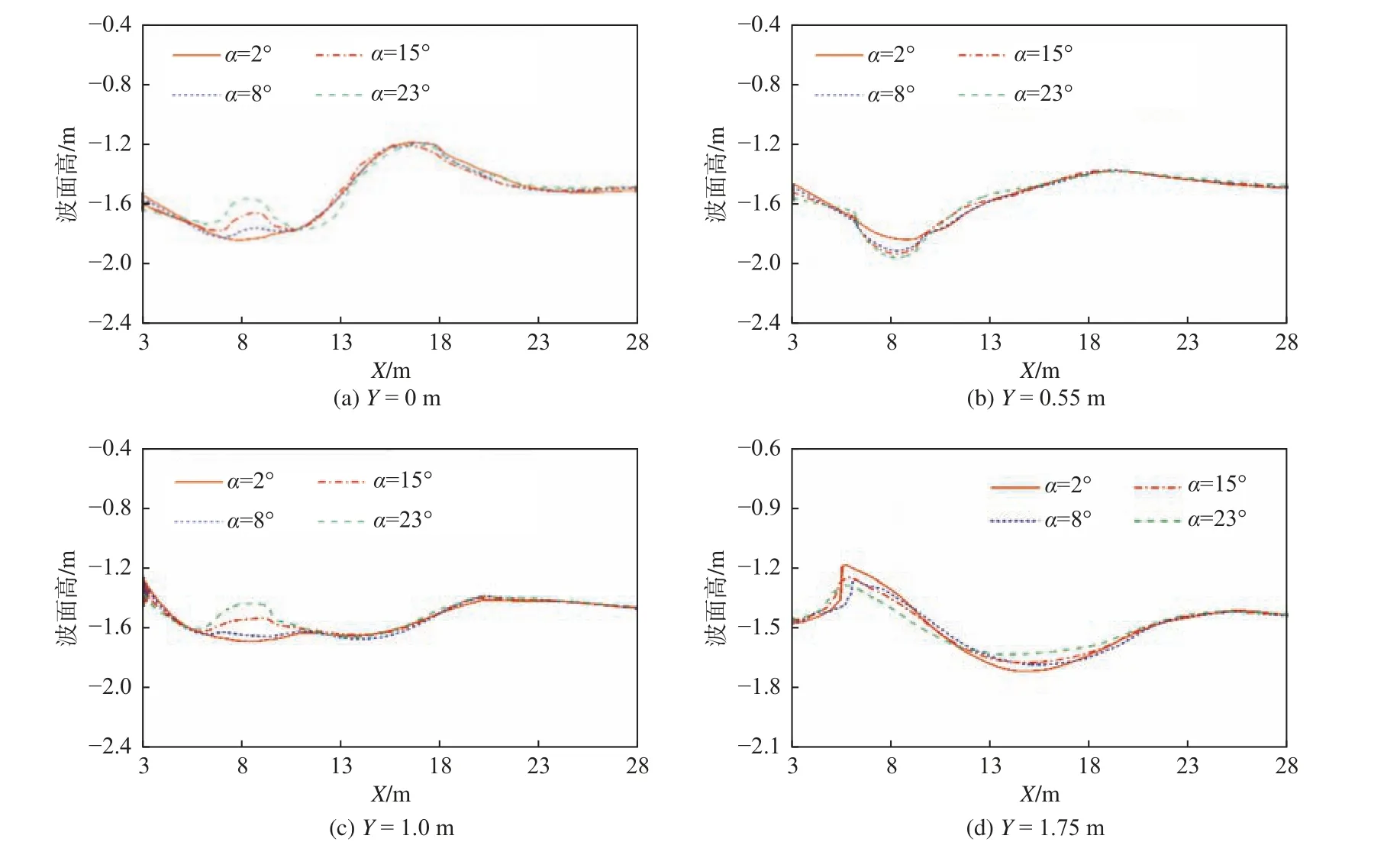
图6 不同纵剖面处波形比较Fig. 6 Comparison of wave height at different longitudinal sections

艉部压浪板不仅对波流场具有影响，其更明显的作用是会影响平台底部的压力分布，从而产生诱导升力。图7 所示为不同α 作用下平台底部的压力分布比较。从中可见，压浪板的存在使平台艉部形成了明显的相对高压区，其主要作用在压浪板的宽度范围，并且α 越大，高压区越明显。截取平台后半部Y= 0.55 m 处平台底面的纵剖线，比较v= 22 kn 速度下不同α 时压浪板及平台底部的相对压力，如图8 所示。压浪板在α 接近于0°时形成的压力峰值不明显，在α = 8°及之后有明显的增加，相对增幅达20%以上，并且在纵向的影响范围也在不断扩大。

图7 不同压浪板下旋角时平台底部相对压力分布Fig. 7 Relative pressure distribution at the bottom of platform under different α

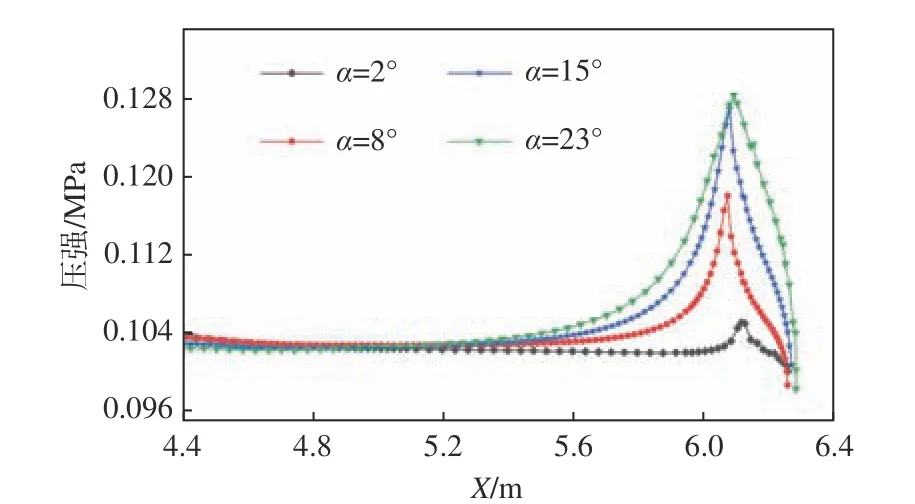
图8 不同下旋角度时压浪板及平台纵剖线相对压力比较（v = 22 kn）Fig. 8 Relative pressure on longitudinal section of platform and stern flap under different α (v = 22 kn)

根据上述分析，压浪板是通过影响底部的压力分布，在艉部产生明显的诱导升力从而形成纵向的埋艏力矩，其对平台纵向运动的影响表现为纵倾角与升沉的减小，故在受到外界扰动时，平台的运动响应越小，越容易保持平稳状态，从而使平台的运动稳定性得到改善。

2.2 纵向运动稳定性分析

2.2.1 设计参数及其对稳定性的影响

定义重心至艉板的纵向距离与平台总长L的比值为r，在相同的重心位置下，航速越高，其运动稳定性越差，而在相同的航速下，重心位置越靠后，越容易导致纵向运动失稳。如图9 所示，当重心与压浪板状态保持不变时，随着航速的增大，其纵倾角的幅度也变大，收敛过程变慢。

图9 不同航速下的姿态收敛情况 (α=15°，r=0.40)Fig. 9 Attitude convergence at different speeds (α=15°, r=0.40)

以比值r、平台航速v以及压浪板下旋角α 为设计变量，r的取值范围为[0.35，0.50]，v的取值范围为[10，28]，在重心纵向位置r和航速v组成的设计空间内随机选取多个样本点，取α=2°，8°，15°，23°，对选取的样本点进行数值计算，并统计各样本点所对应纵向运动稳定性的数值特征。以v= 22 kn，r= 0.43 的工况为例，由图10 所示不同压浪板状态下的纵倾角收敛曲线，发现压浪板的存在同时也减小了平台纵摇的波动，并使其纵摇姿态收敛至基本稳定的值，而相反对于未安装压浪板的情况，其运动姿态的波幅则较大，稳定性得不到保证。

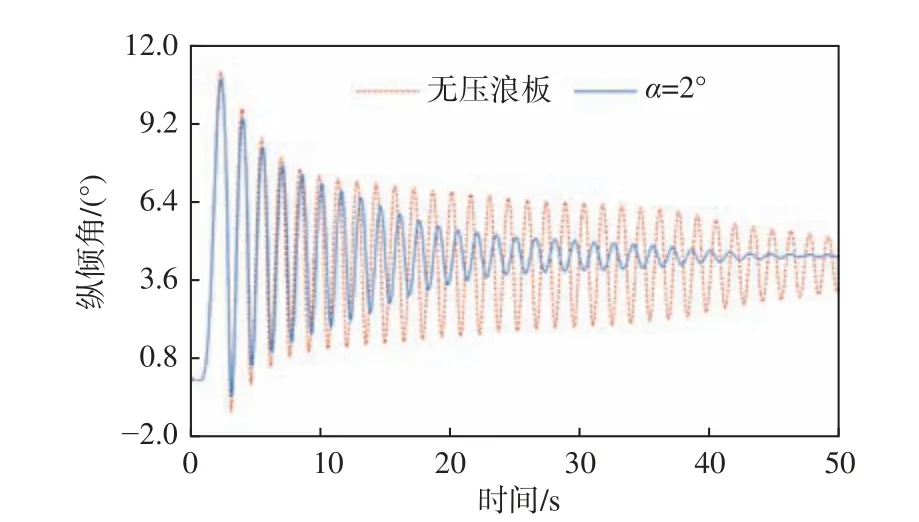
图10 不同压浪板状态下姿态收敛情况 (v=22 kn，r = 0.43)Fig. 10 Attitude convergence at different stern flaps (v=22 kn,r = 0.43)

2.2.2 基于SVM 的运动稳定性分类

基于SVM 的数据分类，其主要原理是确定一个N维的最优分类超平面，在将具有不同数值特征的两类数据分割在超平面两侧的同时，使超平面两侧距离该平面最近的样本数据点之间的间隔最大，然后，以该超平面作为两种类型数据之间的分布边界[17]。当N= 2 时，超平面为二维直线；对于N≥2 的情况，超平面的一般形式为ωTx+b=0，其中，x为数据点， ω为平面法向量，b为平面截距。二维超平面最大间隔优化问题的目标函数为：

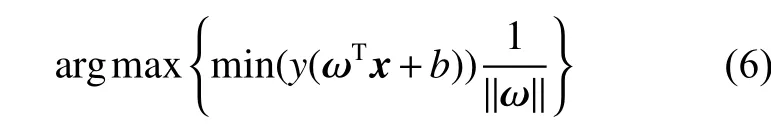
令不同类型数据点的特征标签y= 1 或−1，优化问题的目标函数可以简化为：

针对每一个不同的压浪板下旋角α，将采集到的样本按CFD 计算所得的稳定性特征进行分类，并应用SVM 分类算法找寻其在纵向运动方面的稳定与失稳之间的分类超平面。对于针对不同样本点计算的姿态时历曲线，若其在一定时间内未表现出明显的收敛趋势，则判断该样本点的状态为失稳点，由于在理论上无法确定超平面上点的稳定性特征，为确保稳定性状态分类的可靠性，在赋予采集样本稳定性特征之时，将以28 s作为时间标准，以使所得分类超平面更加偏向于稳定的一侧。图11 所示为不同下旋角压浪板作用下样本点的分类结果。

针对图11 所示分类结果，对分类中因样本点分布的局部密集与稀疏问题可能导致的分类结果不准确问题，降低图中距离分界线太近甚至越过边界的稳态点的速度值，例如在α = 2°情况下r= 0.45 附近的稳态点，以及α = 8°情况下r= 0.47附近的稳态点，并在样本分布稀疏的区域补充新的采样点，如在α = 23°情况下新增r= 0.47，v= 23 kn和r= 0.37，v= 20 kn 这2 个样本点，然后对调整和新增的样本点再次进行CFD 计算，并基于稳定性结果进行数据分类。图12 所示为重新分类完成后的结果，其中各曲线的左上区域为对应α 下的运动不稳定区域。

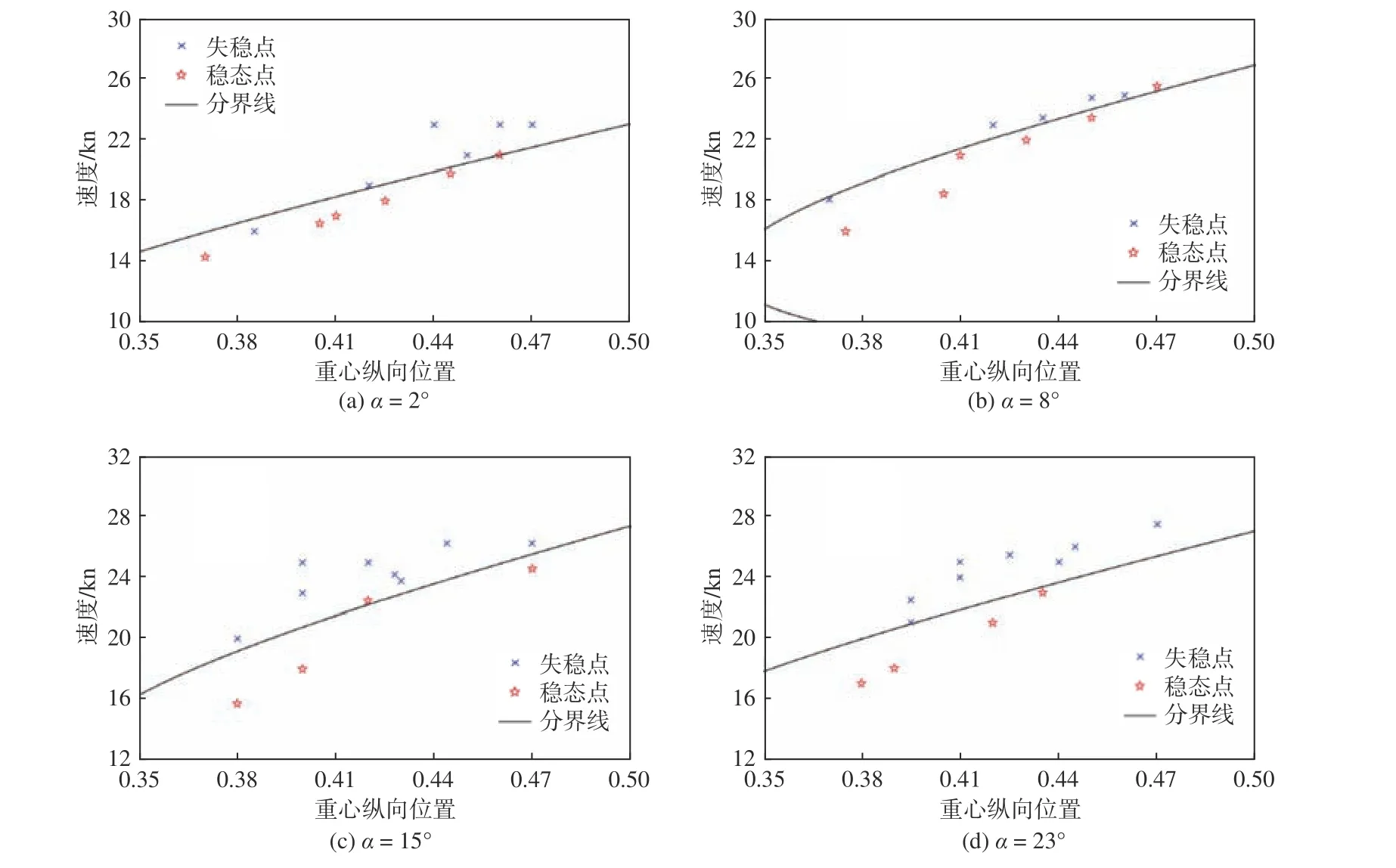
图11 不同下旋角压浪板作用时的稳定性分类结果Fig. 11 Stability classification results at different α

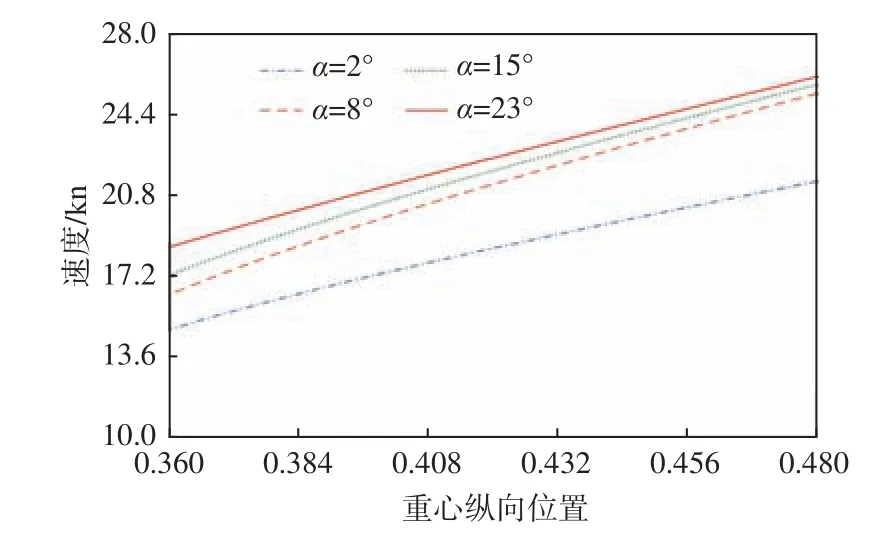
图12 不同下旋角压浪板作用时的平台稳定性边界Fig. 12 Boundary of platform stability at different α

最终，分类得到α=2°，8°，15°和23°压浪板作用下平台运动稳定性边界的数值表达分别如式（12）～式（15）。式中，r代表横坐标的重心纵向位置，也即重心至艉板的纵向距离与平台总长L的比值，s代表两栖平台的航速，也即图12 所示的纵坐标。

根据平台的纵向运动稳定性分类结果，当其他参数因素一定时，通过调节重心的纵向位置，可以提高其在稳定状态下所能达到的速度上限，但由于平台重心前、后位置的变化范围不大，对提高稳定航速的意义不是很大，因此确定两栖平台在无其他附体情况下所能达到的稳定航速不超过21 kn。

而通过在平台艉部加装具有下旋角度的压浪板，则可显著提高平台在不同航速下纵向运动的稳定性。由图12 所示，当压浪板下旋角α 从2°增加到8°时，平台在稳定状态下能够达到的最大航速有明显的提升，但随着α 的继续增大，提升效果逐渐减弱；另通过对比统计不同重心位置下变角度压浪板的作用效果，发现当α = 23°时平台所能达到的最大稳定航速相较于α = 2°时的情况，平均提升幅度约19%，在重心距离艉板0.46L的情况下，最大稳定航速可提升至25 kn。