二维喷动床 CFD -DEM 模拟中曳力模型的影响
2022-07-04周连勇赵永志
周连勇, 赵永志
(浙江大学 能源工程学院 化工机械研究所,杭州 310027)
1 引 言
喷动床作为一种特殊的流化床,具有结构简单和接触效率高等优点[1,2],已经在农作物干燥、生物制药以及能源化工等领域得到广泛应用[3-5]。喷动床的工作效率主要由其内部复杂的气固两相运动决定,而常规的实验方法难以深入探究气固两相运动的机理,无法系统地掌握流动结构和动力学参数。近年来,随着计算机性能的进步和数值模型的不断发展,使用计算机数值模型已经成为研究喷动床的重要手段,实验研究中存留的部分问题也通过数值模拟得到了很好的解决。
目前,喷动床内气固两相运动的数值模拟方法大致可以分类两类,一类是以双流体模型(two-fluid model)为代表的欧拉-欧拉(Euler-Euler)方法[6-8],该方法把固体颗粒相和气相都看作连续相;另一类是以CFD -DEM(computational fluid dynamics coupled with discrete element method)为代表的欧拉-拉格朗日(Euler-Lagrangian)方法[9-12],该方法把固体颗粒相看做离散相,把气相看作连续相。相较于双流体模型,CFD -DEM可以追踪单个颗粒运动,获得颗粒尺度的微观信息,在喷动床内部气固两相运动机理的探究以及喷动床结构的优化设计中逐渐成为主流。根据颗粒周围流场的解析程度,CFD -DEM又可以分为解析的(resolved)CFD -DEM[13-15]和未解析的(unresolved)CFD -DEM[16-18],其中解析的CFD -DEM要求流体网格尺度是颗粒尺度的1/10以解析颗粒边界[19],其计算结果非常精确,但是计算量对于工程尺度的模拟而言过于巨大,而未解析的CFD -DEM框架下流体网格尺度可以是颗粒尺度的3倍以上[20,21]。因此,得益于计算效率的显著优势,未解析的CFD -DEM广泛应用于工业级喷动床的数值模拟当中,也是本文采用的研究方法。由于未解析的CFD -DEM流体网格分辨率低,气固两相间最重要的作用力,即曳力的计算需要引入额外的曳力模型,曳力模型的精度很大程度上决定了未解析CFD -DEM模拟的准确性,因此研究不同曳力模型对模拟结果的影响具有重要意义。目前,关于曳力模型的比较研究大多是在传统流化床中进行的[22-24],有些在喷动床中进行的其计算域的离散使用的也是结构化网格[11],在非结构化网格喷动床中进行的比较研究还未见报道。
综上,本文基于未解析CFD -DEM和非结构化网格,使用7个曳力模型分别对锥底喷动床内气固两相运动进行了数值模拟并比较不同曳力模型对模拟结果的影响,以期揭示不同曳力模型的作用效果,为曳力模型的选择提供依据。
2 CFD -DEM模型
2.1 颗粒运动方程
DEM通过求解牛顿第二定律描述颗粒运动,
(1,2)
式中m和I分别为颗粒质量和惯性张量,v和ω分别为线速度和角速度,Fc为法向接触力和切向接触力的矢量和,Fd为曳力,g为重力加速度,Tc为由切向接触力引起的接触力矩。颗粒运动方程详见文献[25-28],本文不再赘述。
2.2 气相控制方程
在未解析CFD -DEM框架下,气相的运动由局部平均化Navier-Stokes方程描述,

(3)

(4)
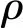
(5)
式中Vp,i为颗粒体积,n为CFD单元的颗粒总数,ΔV为CFD单元的体积。
2.3 曳力模型
在多颗粒系统中,作用在单个颗粒上的曳力可以表示为
(6)
式中dp为颗粒直径,αs为固含率,β为相间动量交换系数。
现有的曳力模型可以分为两类,一类是通过床层压降测量和颗粒沉降测试等实验方法获得的传统曳力模型,如Wen-Yu模型[29]、Di Felice模型[30]、Gibilaro模型[31]、Gidaspow模型[32]、Huilin-Gidaspow模型[33](简称Huilin模型)和Syamlal-O’Brien(简称Syamlal模型)模型[34];另一类是借助如格子玻尔兹曼方法(Lattice -Boltzmann method)和直接数值模拟(direct numerical simulation)等先进的数值计算方法得到的曳力模型,如BVK模型[35]。本文考虑了以上7个常用的曳力模型。
Wen-Yu模型[29]是最早出现的几个曳力模型之一,其基于单颗粒曳力函数,引入颗粒体积分数修正因子对曳力模型进行修正,并且考虑了周围粒子的影响。Wen-Yu模型[29]适用于稀相系统,其可表示为
(7)
(8)

(9)
Gidaspow模型[32]结合了Ergun方程[36]和Wen-Yu模型[29],固含率较低时使用Wen-Yu模型[29],固含率较高时使用Ergun方程[36],其相间交换系数的计算如下,
(10)
式中CD的计算同Wen-Yu模型。
Huilin模型[33]也是Ergun方程[36]和Wen-Yu模型[29]的组合,利用一个平滑过渡函数Ψ解决了Gidaspow模型[32]在计算空隙率跨越 0.8 的稠密气固两相流时曳力在数值上不光滑的问题,其可表示为
(11)

(12)
式中CD的计算同Wen-Yu模型。
Di Felice[30]通过对颗粒堆积体内渗流实验数据的整理和拟合推导出Di Felice曳力模型[30],该模型认为颗粒堆积体内流体对颗粒的作用力可以表达为单颗粒在流体内平稳沉降时所受的曳力与孔隙函数的乘积,
(13)
γ=3.7-0.65exp [-(1.5-lg Rep,α)2/2]
(14)
(15)
式中 Rep,α的计算同式(9)。
Gibilaro模型[31]也适用于稀相系统的曳力模型,可表示为
(16)
式中 Rep,α的计算同式(9)。
Syamlal模型[34]是基于测量颗粒在流化床或沉降床中的终端速度得到的。
(17)
(18)
vr=0.5(A-0.06Rep)+0.5·[(0.06Rep)2+
0.12Rep(2B-A)+A2]0.5
(19)
(20,21)

(22)
BVK模型[35]是基于大规模数值计算推导得到的,可表示为
(23)
(24)
式中 Rep,α的计算同式(9)。
2.4 流体速度插值
根据2.3节的介绍可知求解曳力时需要获得颗粒位置处流体的速度,传统做法是直接使用颗粒所在网格储存的平均速度作为颗粒位置处的流体速度,但是在未解析CFD -DEM框架下网格尺度要大于颗粒尺度的3倍以上,这导致网格尺度的平均速度无法准确反应颗粒局部的流体运动情况,因此将网格尺度的平均速度插值到颗粒位置处是非常重要的。本文采用基于梯度的插值方法[37,38]获得颗粒位置处的流体速度,其中网格的速度梯度使用最小二乘法[39]获得,具体插值表达式为
up=uc+u·rc p,rc p=xp-xc
(26,27)
式中up为颗粒位置处的流体速度,uc为网格储存的平均流体速度,rc p为网格质心指向颗粒位置的向量,xp为颗粒位置,xc为网格质心位置。
3 模拟条件及求解
本文的研究对象为锥底喷动床,如图1(a)所示。床体高度为890 mm,宽度为250 mm,厚度为10 mm,呈现出典型的准二维结构。锥底角度为60°,喷口宽度为20 mm,气室高度为100 mm,气体从气室底部进入,从床体顶部流出。如图1(b)所示,整个计算域用非结构化网格离散,其中最小网格的尺寸约为颗粒粒径的3倍,最大网格的尺寸不超过颗粒5倍以保证计算精度和稳定性。模拟中使用的颗粒为相同粒径的球形玻璃颗粒,气体为空气,具体的物性信息及模拟中使用的参数列入表1。本文分别使用7个曳力模型进行数值模拟,每个算例除了曳力模型不同外其余设置均相同,入口边界条件设置为速度入口,气速为恒定的10 m/s,出口边界条件设置为压力出口,壁面设置为无滑移壁面。每个算例开始时颗粒均堆积在床层底部,然后在入口气体的作用下形成喷动现象。
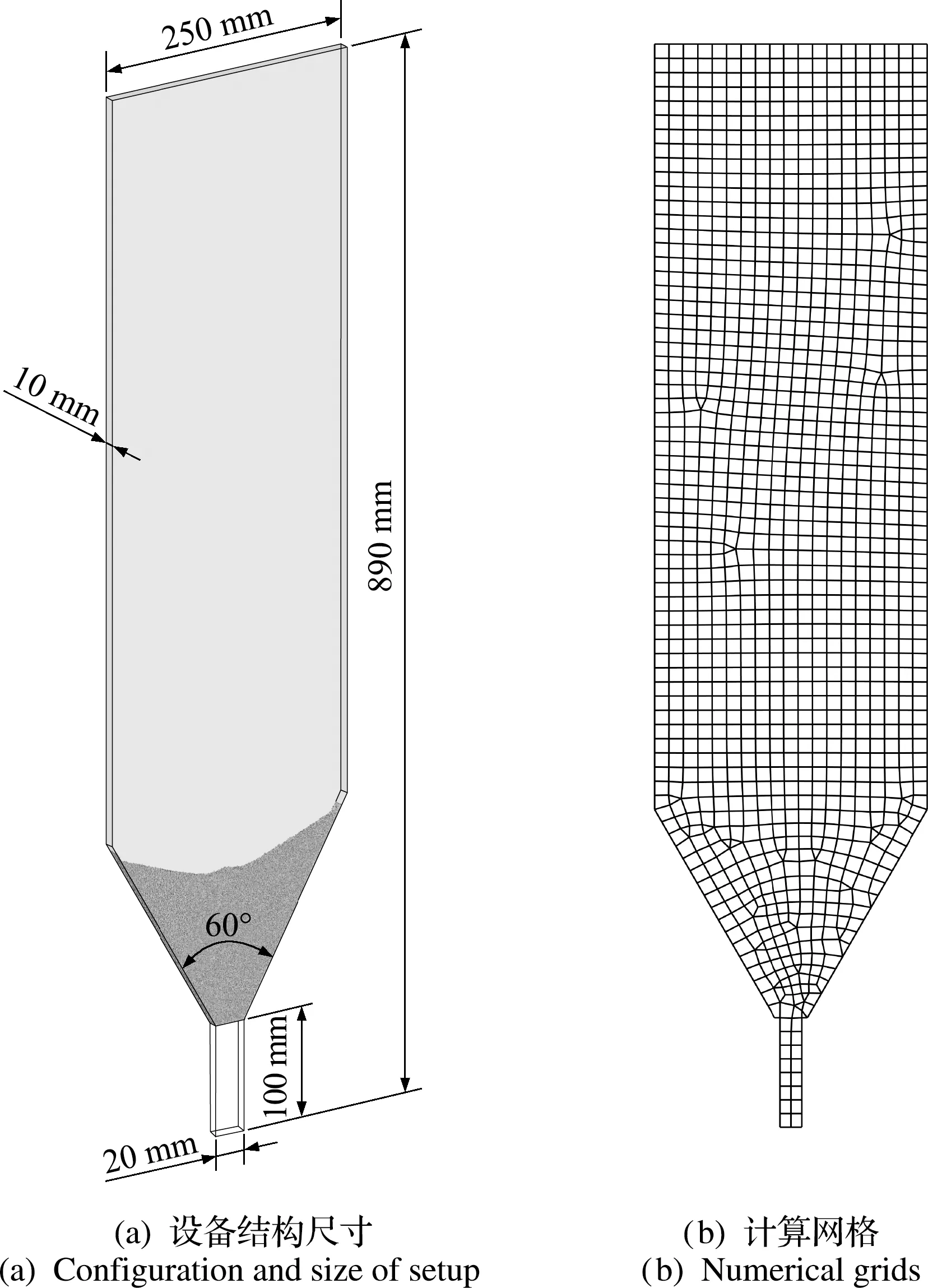
图1 设备结构尺寸及计算网格

表1 模拟中使用的参数
对于连续相,采用SIMPLE算法进行求解,时间项、对流项和扩散项分别使用Crank-Nicolson格式、QUICK格式和中心差分格式离散。对于颗粒相,采用自主开发的DEM代码进行求解,其中颗粒运动的计算方法为显示时间积分法。每个算例均计算15 s,其中前5 s的数据丢弃,只用后10 s的数据进行统计平均以排除初始效应。更多关于 CFD -DEM 耦合的细节可以参见文献[25,40],本文不再赘述。
4 结果与讨论
4.1 床层压降
在模拟中监控气室入口和床体顶部的压力值,二值之差即为床层压降。床层压降及其相关分析可以反映床内气固两相运动的剧烈程度,是衡量模型准确性的重要指标,因此本文也使用床层压降来分析不同曳力模型对模拟结果产生的影响。
图2为时均床层压降及其标准差,可以看出,7种模型预测的时均压降处于同一水平,均在1480 Pa左右,但相应的标准差却呈现出明显差异,其中Wen-Yu模型和Gibilaro模型预测的标准差较大,分别为260 Pa和272 Pa,说明在这两种模型作用下两相系统运动最剧烈。Di Felice模型预测标准差小于Wen-Yu模型和Gibilaro模型,约为195 Pa,Syamlal模型、Huilin模型以及Gidaspow模型预测的标准差相似,均为155 Pa左右,BVK模型预测的标准差最小,为132 Pa。更进一步地,可以通过离散傅里叶变换获得床层压降的频域信息,如图3所示。可以看出,除BVK模型外,其余模型预测的压力信息都有明显的主频,大约为3 Hz,符合实验室规模喷动床的主频范围。Wen-Yu模型和Gibilaro模型预测的主频幅值最大,均超过了100 Pa,其次是Di Felice模型和Syamlal模型,介于50 Pa~100 Pa,最后是Gidaspow模型、Huilin模型和BVK模型,三者预测的主频幅值均低于50 Pa。

图2 时均床层压降及标准差
通过对床层压降的分析可知,Wen-Yu模型和Gibilaro模型预测的床层运动最剧烈,BVK模型预测的床层运动最平缓,其余四个模型的预测效果介于中间。此外,可以发现Gidaspow模型和Huilin模型的预测结果几乎一致,这是因为本文研究的气固两相体系属于密相体系,光滑过渡函数没有产生效果。
4.2 喷动高度
对不同高度处颗粒轴向速度的时均处理可以得到每个曳力模型预测的喷动高度,如图4所示。可以看出,Wen-Yu模型预测的喷动高度最大,达到了279 mm,其次是Di Felice模型和Gibilaro模型,分别为267 mm和261 mm,Gidaspow模型和Huilin模型预测的喷动高度相同,均为255 mm,再是Syamlal模型,预测喷动高度为249 mm,最后是BVK模型,预测喷动高度为最小的243 mm。
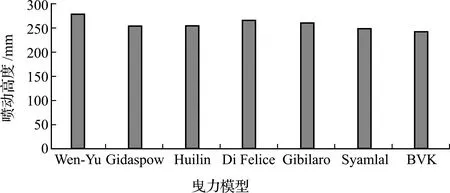
图4 不同曳力模型预测的喷动高度
为了更直观地展示不同曳力模型对喷动床喷动高度的影响,图5给出了2 s后不同曳力模型模拟的瞬态快照。可以看出Wen-Yu模型和Gibilaro模型的算例中颗粒运动最剧烈,喷动高度最高,BVK模型计算得到的喷动高度最低,其余四种模型的计算结果介于中间,这与喷动高度定量统计的结果一致。此外,由于在计算颗粒位置处的流体速度时使用了梯度插值的方法,图5展示的瞬态快照没有呈现出明显的网格效应,气相和颗粒相的分界面比较光滑。

图5 2 s后的颗粒运动快照
可以看出,对喷动高度的分析得到了与床层压降分析几乎一致的结论,Wen-Yu模型和Gibilaro模型由于稀相适用性导致其在本文研究的密相喷动床中预测得到最剧烈的气固两相运动,因此统计的压降波动和喷动高度也最大,而通过LBM得到的BVK模型计算得到的气固两相运动最平缓,相应的压降波动和喷动高度也是所有模型中最小的。
4.3 颗粒轴向速度
图6展示了各个曳力模型的时均颗粒轴向速度的径向分布(距离气体入口190 mm处)。可以看出各曳力模型的预测结果均呈现出中心正,边壁负的分布特征,说明颗粒在喷动床中心区域向上运动,沿径向颗粒速度逐渐减小,直至近壁面区域颗粒向下运动,颗粒在喷动床锥部形成了典型的环-核流动结构,这种结构特征已得到广泛报道[1,41-43]。对比各个曳力模型的模拟结果发现,Wen-Yu模型和Gibilaro模型预测的轴向速度最大,其次是Di Felice模型,Syamlal模型、Gidaspow模型和Huilin模型的预测结果非常接近,BVK模型预测的轴向速度最小。

图6 190 mm高度处的颗粒时均轴向速度
5 结 论
本文基于未解析的CFD -DEM和非结构化网格,在锥底喷动床中比较了Wen-Yu模型、Gidaspow模型、Huilin模型、Di Felice模型、Gibilaro模型、Syamlal模型和BVK模型七个曳力模型对模拟结果产生的影响。综合床层压降、喷动高度和颗粒速度特性三个方面,Wen-Yu模型和Gibilaro模型预测的气固两相运动最剧烈,其次是Di Felice模型、Syamlal模型、Gidaspow模型和Huilin模型,BVK模型预测的气固两相运动最平缓。此外,由于本文研究的气固两相体系属于密相体系,Huilin模型的光滑过渡函数没有产生效果,所以Gidaspow模型和Huilin模型在各个方面的预测结果基本一致。此外,如果想判定特定工况下最优的曳力模型,还需要进一步的实验加以对照。
