基于多滑模变结构的双向并网变换器虚拟惯性控制策略
2022-07-04刘彦呈吕旭张勤进胡王宝张瀚文
刘彦呈,吕旭,张勤进,胡王宝,张瀚文
(大连海事大学轮机工程学院,辽宁省 大连市 116026)
0 引言
为应对日益严峻的化石能源枯竭和环境污染问题,以新能源发电为主的分布式发电技术得到了广泛关注[1-3]。 光伏、蓄电池等直流电源的大规模接入及负荷侧对直流功率需求的与日俱增促进了直流微电网的迅速发展[4-10]。 但直流微电网作为以电力电子变换器为主导的低惯性系统,当网内出现由光伏、风电等间歇性电源输出功率波动及负载频繁投切造成的扰动时,母线电压会遭受到较大冲击而剧烈波动,危害直流微电网的稳定运行[11-13]。
双向并网变换器(bidirectional grid-connected converter, BGC)是连接直流微网与大电网的并网控制端口,在维持直流微网与大电网间能量的双向流动, 稳定直流母线电压等方面承担关键作用[14-15]。
针对直流微网惯性低、母线电压抗干扰能力差的问题,文献[16]通过类比交流微网中的虚拟同步发电机控制提出一种应用于直流微网双向并网变换器的虚拟惯性控制策略。 通过在传统电压环外加入虚拟惯性方程,在变换器直流侧模拟电容的稳压特性,从而增强直流微网的惯性,抑制直流母线电压波动。
然而,虚拟电容的引入会降低系统的动态响应速度,导致暂态下直流母线电压的恢复时间变长。文献[17]通过建立直流电压变化率与虚拟电容之间的函数关系,提出灵活虚拟惯性控制策略。 然而,仅通过调节虚拟电容值对系统动态性能的改善作用有限,且虚拟电容的频繁切换可能会导致母线电压振荡。
目前,大量关于BGC 虚拟惯性控制(virtual inertia control, VIC)策略的研究,在闭环控制中仍采用传统的比例积分(proportion integration,PI)控制,然而PI 控制很难使非线性系统获得较好的动态性能。 因此,为改善功率扰动下母线电压的动态性能,有学者提出将非线性控制算法引入到虚拟惯性控制策略中。 文献[18] 提出一种基于无源控制(passivity-based control, PBC)的虚拟惯性控制策略,从能量角度出发设计了基于欧拉-拉格朗日(Euler-Lagrange, EL)模型的电流内环无源控制器,通过调节注入的阻尼大小使网侧电流收敛到给定值。 该方法减小了直流电压波动,但系统调节时间较长。 由于无源控制对系统模型和参数的依赖度高,导致受扰下系统很难获得良好的跟踪效果。
滑模变结构控制[19-21](sliding mode control,SMC)因系统在进入滑模运动后不受系统参数变化及外界扰动的影响而具有较强的鲁棒性,且其具有控制算法简单、动态响应速度快等优点,将其引入BGC的虚拟惯性控制中可以有效改善系统的动态特性,增强直流母线电压的抗扰能力。 文献[22]将多滑模控制算法引入三相脉宽调制(pulse width modulation,PWM)整流器中,改善了直流电压波动和响应速度,但电流环引入滑模算法产生的抖振问题使并网电流谐波较大。 文献[23]提出一种基于多滑模变结构的网侧整流器控制策略,设计了电压滑模面和电流滑模控制律。 为削弱滑模抖振,采用基于指数趋近律的滑模电流控制,在提高直流电压动态特性的同时保证了网侧电流谐波畸变率低。
因此,为改善直流母线电压的动态性能,同时增强直流微网的惯性,本文提出一种基于多滑模变结构的双向并网变换器虚拟惯性控制策略。 内环采用基于指数趋近律的滑模电流控制,快速跟踪并网电流给定值;外环建立虚拟惯性方程与电压滑模面结构,增强直流母线电压的稳定性。 通过小信号建模分析BGC 系统在本文所提控制方法下的稳定性,并给出虚拟惯量的选取范围。 最后,通过仿真和实验验证所提控制策略的有效性。
1 含BGC 接口的直流微电网结构
图1 为含BGC 接口的直流微电网拓扑结构图,该直流微电网主要由双向并网变换器、分布式电源、储能装置、负载以及相应的功率变换器组成。 当直流微电网运行于并网模式时,BGC 采用直流侧恒压控制,平衡直流微电网内的功率盈缺,稳定直流母线电压。 当交流电网出现故障时,直流微电网切换到孤岛模式,BGC 退出运行,直流微电网的母线电压由储能装置进行维持。

图1 含BGC 的直流微电网结构图Fig.1 Diagram of DC micro-grid with BGC
本文为着重分析并网模式下BGC 的控制策略,将BGC 直流侧的分布式电源、储能及相应的功率变换器等效为功率源Pcs,负载侧接入恒功率负载(constant power load, CPL)。 简化后的含BGC 的直流微电网等效结构如图2 所示。 图2 中,Q1—Q6分别为BGC 主电路三相桥臂的6 个绝缘栅双极型晶体管(insulated gate bipolar transistor,IGBT) 开关管。um(m=a,b,c)为三相电网电压,im为三相并网电流;em为BGC 交流侧端电压,udc为BGC 直流侧母线电压;idc为桥臂直流侧输出电流;i0为BGC 直流侧输出电流,iR为直流侧负载电流。L和R分别为交流侧滤波电感和电阻,C为直流侧稳压电容。 为维持直流微网内电源和负载的功率平衡,BGC 会根据差额功率传输方向的变化在整流和逆变工作状态间自主切换,以保证直流母线电压恒定。
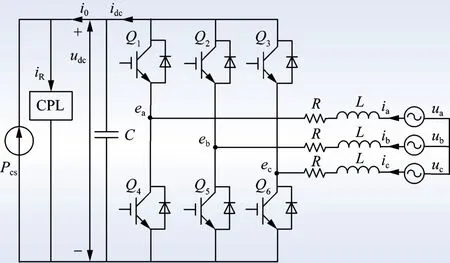
图2 含BGC 的直流微电网等效结构图Fig.2 Equivalent diagram of DC micro-grid with BGC
2 基于多滑模变结构的BGC 虚拟惯性控制
2.1 电压外环滑模控制器设计
假设BGC 主电路功率开关器件均为理想开关,开关频率远高于电网的基波频率。 交流电网等效为理想三相电压源,网侧滤波电感三相平衡,根据图2,基于等值变换建立BGC 系统在同步旋转dq坐标系下的数学模型:
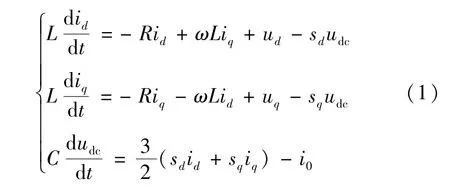
式中:ud和uq分别为三相电网电压ua、ub和uc在dq轴的电压分量;id和iq分别为三相电网电流ia、ib和ic在dq轴的电流分量;sd和sq分别为开关函数在dq轴的分量;ω为交流电网的角频率。
由式(1)可知BGC 系统有sd和sq两个控制量,其中sd用于控制直流侧电压udc,sq用于控制无功电流分量iq。 以udc和iq作为输出变量,分别选取其跟踪误差σu和σq作为系统的状态变量,设计电压外环滑模控制器,滑模面函数S(·)为:
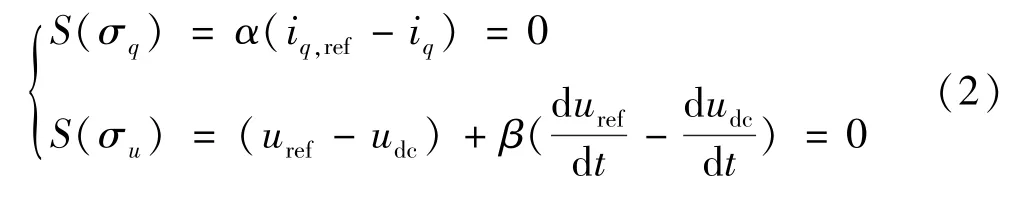
式中:α、β为电压滑模面参数;iq,ref为网侧无功电流的给定值;uref为直流侧电压的给定值。
将式(1)代入到式(2)中得:

将式(3)改写为:
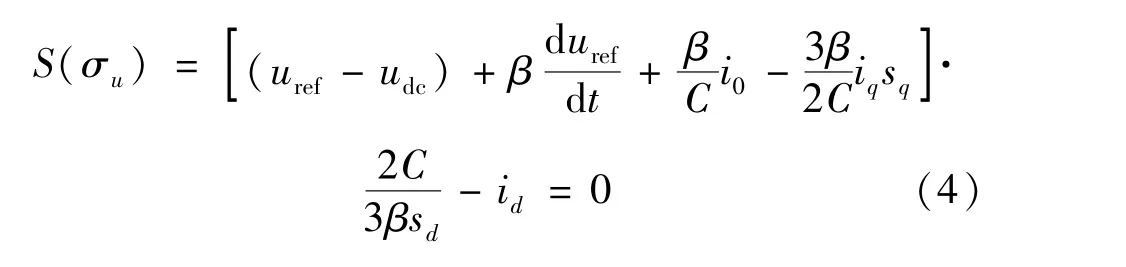
在BGC 系统中,考虑网侧电压三相平衡,BGC以单位功率因数运行,则稳态条件下,对式(1)中的控制量进行化简:
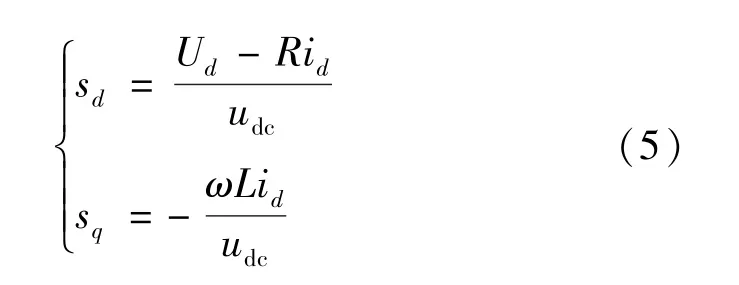
式中:Ud为电网电压在d轴的稳态分量。
将式(5)代入式(4)化简得到:
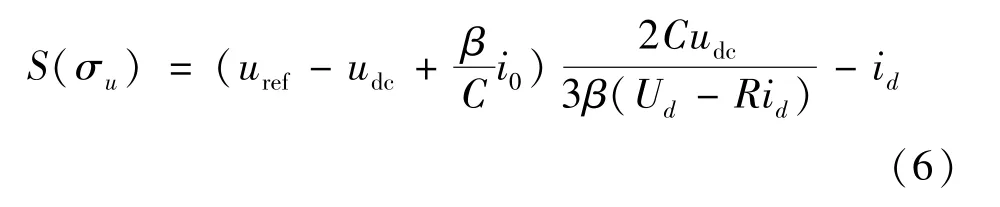
由此,得到电压外环的滑模控制方程,电压外环的输出作为内环电流有功分量的给定值,即:
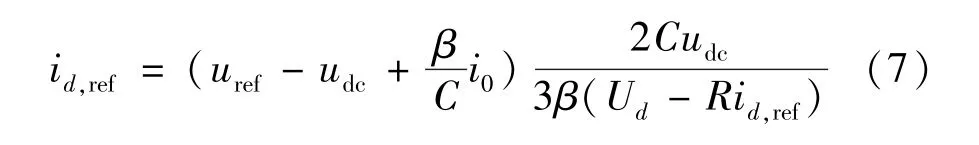
式中:id,ref为网侧d轴有功电流分量的给定值;β为电压滑模面的偏差放大系数。 有研究表明[24]偏差放大系数的确定要考虑开关的死区和延时,其值不能过大,一般取值为0.01 ~0.10,经仿真调试,本文β取值为0.05。
2.2 电流内环滑模控制器设计
电流内环滑模控制器的控制目标为:通过控制变量sd和sq,使dq轴电流分量id和iq跟随电流给定值id,ref和iq,ref,令iq,ref=0,实现单位功率因数控制。 分别以网侧电流dq分量的跟踪误差σd和σq作为状态变量设计滑模面函数S(·):
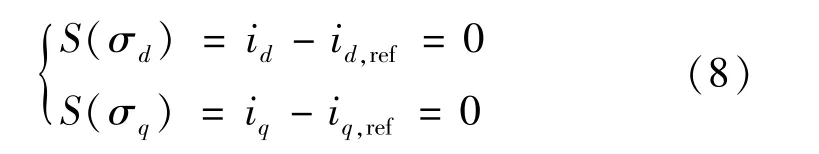
为抑制因滑模控制律的不连续导致的抖振,改善滑模到达段的运动,采用指数趋近律来设计电流内环滑模控制律,即:
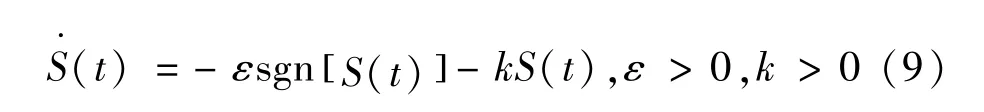
式中:ε为系统运动点趋近滑模面的速度,选取较小的ε值使系统状态距离滑模面较近时降低趋近速度,避免状态轨迹到达滑模面后产生强烈的抖振;k为指数趋近项系数,选取较大的k值使系统状态在距离滑模面较远时快速趋近滑模面。 本文综合考虑内环响应速度及滑模抖振的影响,在保证系统稳定约束条件下电流滑模控制的参数选取范围为:100 <k<1000,0 <ε<100。 经仿真调试后,本文选取动态性能较佳的一组参数:kd=kq=500,εd=εq=100。 其中εd和εq,kd和kq分别为dq轴内环电流滑模控制器的相关参数。
结合式(1)、式(9),对内环电流进行前馈解耦,得到电流内环的滑模控制方程:
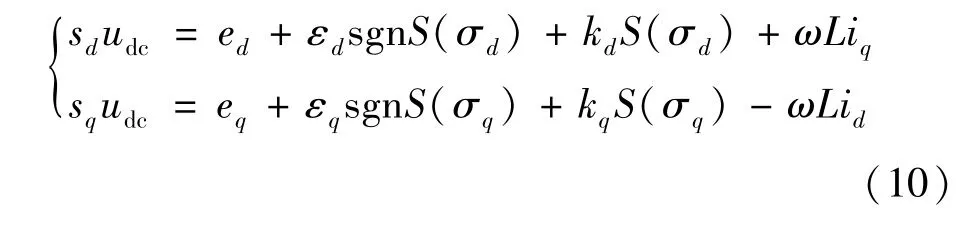
对式(8)求导,并联立式(1)、式(10)可得:
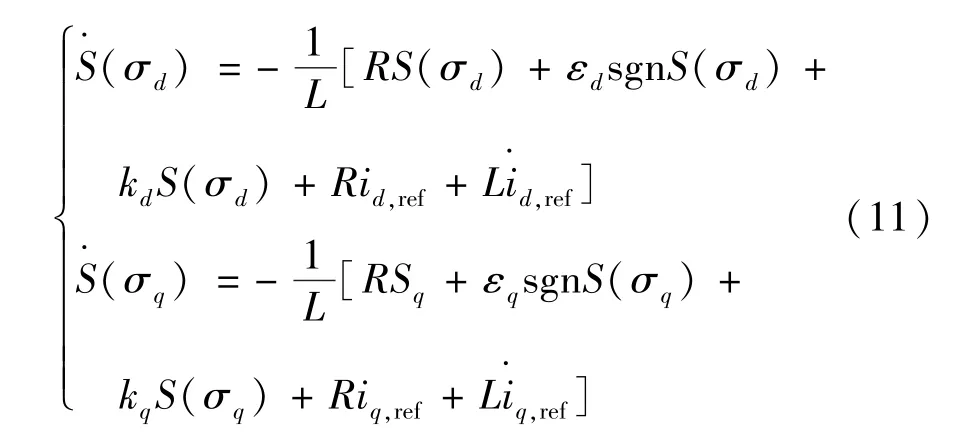
为确保滑模控制算法的可达性及稳定性,需满足以下条件:

将式(8)、式(11)代入式(12)得:
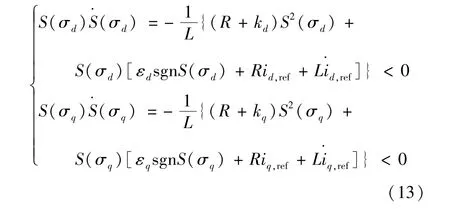
可推导出满足式(13)的滑模控制参数:
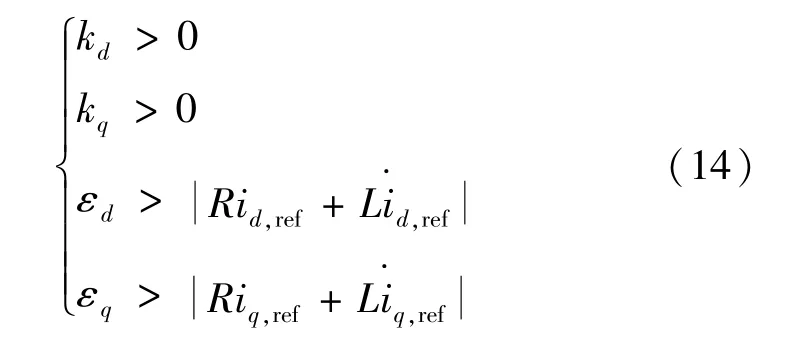
上述控制参数同时满足式(15)给出的李雅普诺夫函数V是非正定的,即证明滑模控制系统趋于稳定。
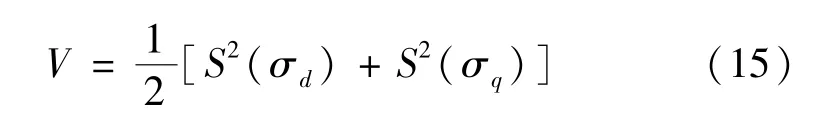
2.3 BGC 虚拟惯性控制策略
交流微网中的VSG 控制策略基于有功-频率下垂控制使逆变器模拟出同步发电机的旋转惯性及阻尼特性,当电网频率突变时,虚拟惯量J的引入使VSG 输出的有功功率得到快速调节,从而使逆变器对电网频率具有一定的惯性支撑,有效抑制了电网频率的大幅波动。 VSG 的有功-频率下垂方程为:
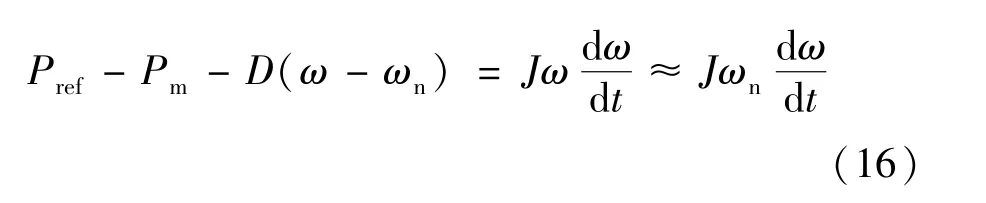
式中:Pref和Pm分别为给定有功功率和VSG 输出有功功率;ωn为交流电网额定角频率;J和D分别为VSG 控制中的虚拟转动惯量和频率阻尼系数。
根据文献[16]给出的类比VSG 控制的直流微网虚拟惯性控制策略,交流微网中的角频率、有功功率及虚拟转动惯量与直流微网中的直流母线电压、直流侧输出电流及直流侧虚拟电容存在对应关系。 据此,本文采用的虚拟惯性控制方程为:

式中:Iref为BGC 输出电流给定值;Dv为电压阻尼系数;Un为直流侧电压额定值;uref为虚拟惯性环节输出的直流电压参考值;Cv为虚拟电容值。
通过式(17)可知,当直流微网内功率波动导致直流母线电压突变时,通过虚拟电容Cv迅速调节BGC 直流侧输出电流,从而增强直流微网的惯性。理论上,Cv值越大,直流微网的惯性越强。
因此,结合式(7)、式(10)和式(17)给出的控制方程,建立引入多滑模变结构的VIC 策略的BGC 系统控制框图,如图3 所示。
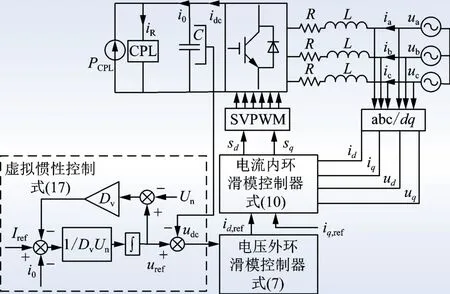
图3 BGC 系统控制框图Fig.3 Block diagram of BGC system control
3 小信号稳定性分析
为进一步分析引入多滑模控制算法的虚拟惯性控制策略对BGC 系统影响,建立所提控制策略下BGC 的小信号模型并分析系统的稳定性。
首先建立电流内环的小信号模型,考虑到d轴和q轴的电流环具有对称性,为简化分析,本文以d轴电流环为例。 设电流调节器的等效传递函数为Gi(s),得到电流内环的小信号方程:
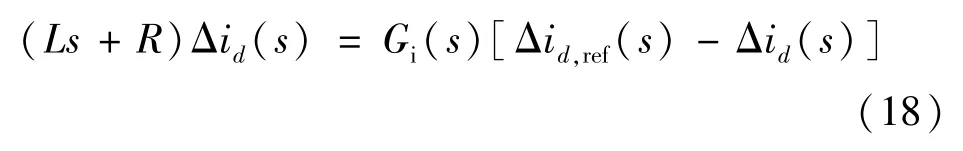
式中:s为拉普拉斯算子;Δid和Δid,ref分别为网侧d轴电流和d轴电流给定值的小信号扰动量。
采用基于指数趋近律的内环滑模电流控制替换传统内环PI 控制,即:
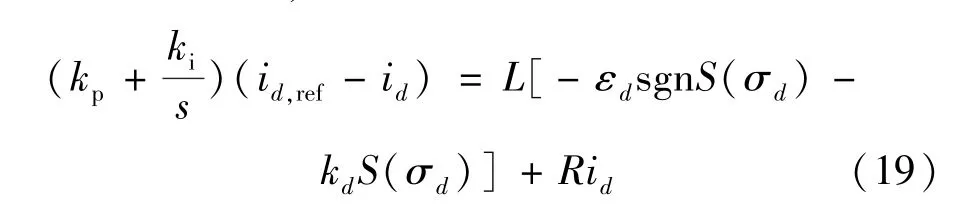
对式(19)右侧分段线性化可得:
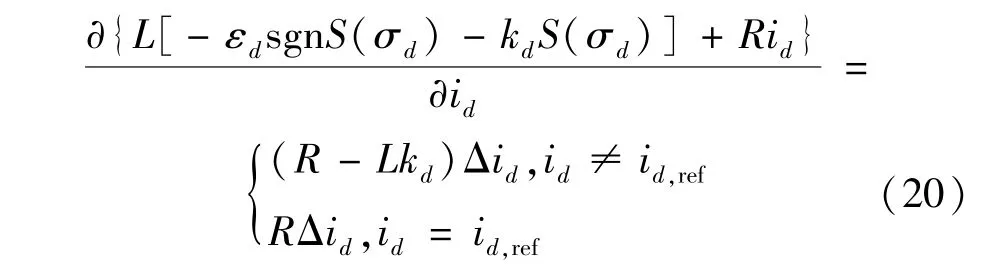
由式(20)可知,滑模电流控制对系统小信号扰动的稳定性可等效为内环PI 控制环节中ki=0,kp取值为(R-Lkd)或R时的稳定性。 与PI 控制相比,滑模电流控制减少了积分环节,在避免了内环积分系数较小引起不稳定影响的同时,提高了内环的响应速度。 因此,滑模电流控制的等效传递函数Gi(s)可表示为:
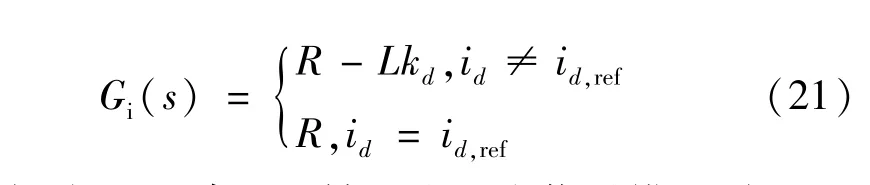
根据式(18)建立d轴电流环小信号模型,如图4所示,其中Kpwm为桥路PWM 等效增益。

图4 d 轴电流环小信号模型Fig.4 Small-signal model of d-axis current
下面建立滑模电压外环的等效传递函数Gv(s),并推导引入虚拟惯性控制环节的BGC 系统的小信号模型。
根据式(7)所给出的电压滑模方程,将式中的状态变量写成稳态量和小信号扰动量之和,即uref=Uref+Δuref,udc=Udc+Δudc,忽略电流扰动项Δi0和二次扰动项,根据叠加原理可得:
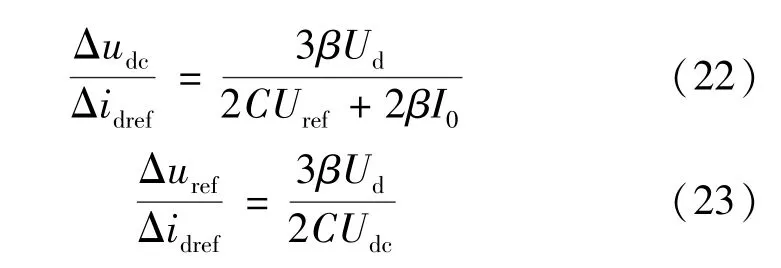
式中:Δudc和Δuref分别为BGC 直流侧母线电压和母线电压给定值的小信号扰动量;Udc为BGC 直流侧母线电压的稳态值。
由此可推导出滑模电压控制的等效传递函数:
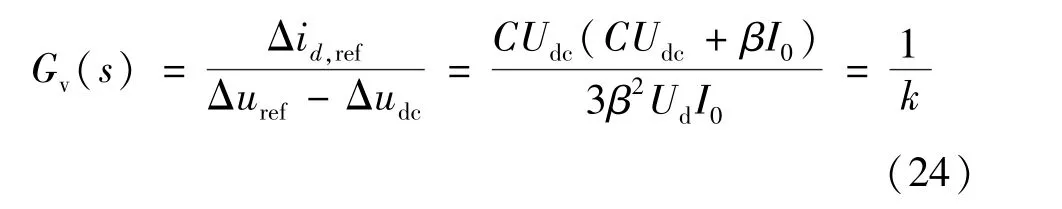
由式(24)可知滑模电压控制的传递函数可等效为线性比例控制环节,式中k为比例常数。
设定BGC 运行于单位功率因数,即无功电流分量iq=0,根据BGC 交、直流侧功率平衡有:
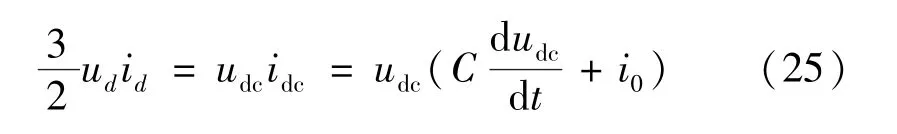
将式(25)中的状态变量改写为稳态量与小信号扰动量之和,即i0=I0+Δi0,udc=Udc+Δudc,忽略电网电压扰动项Δud和二次扰动项,式(25)小信号方程为:
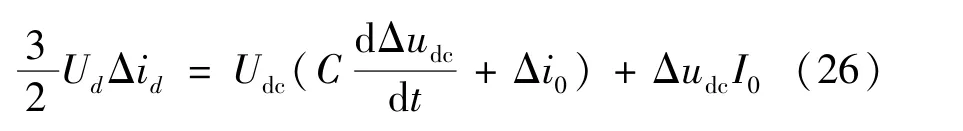
式中:Δi0和I0分别为BGC 直流侧输出电流i0的小信号扰动量和稳态值。
根据叠加原理,对式(26)进行拉普拉斯变换可得:
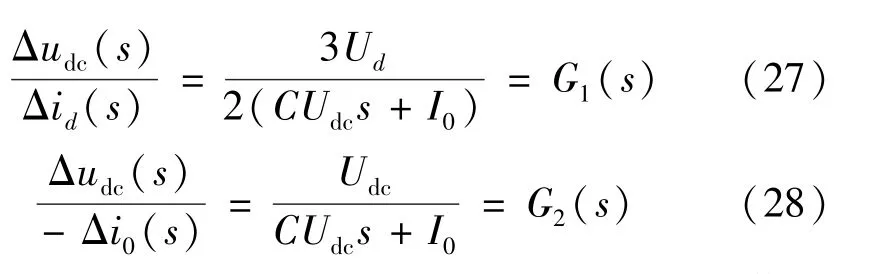
对式(18)给出的虚拟惯性控制方程进行小信号分析得:
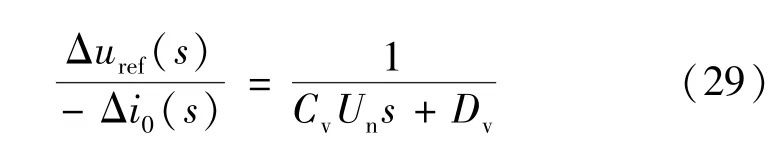
据此,建立BGC 系统的小信号模型如图5 所示。

图5 BGC 系统的小信号模型Fig.5 Small-signal model of BGC system
根据图5,推导BGC 系统闭环传递函数G(s):
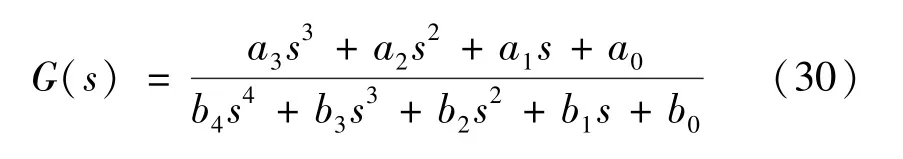
其中,
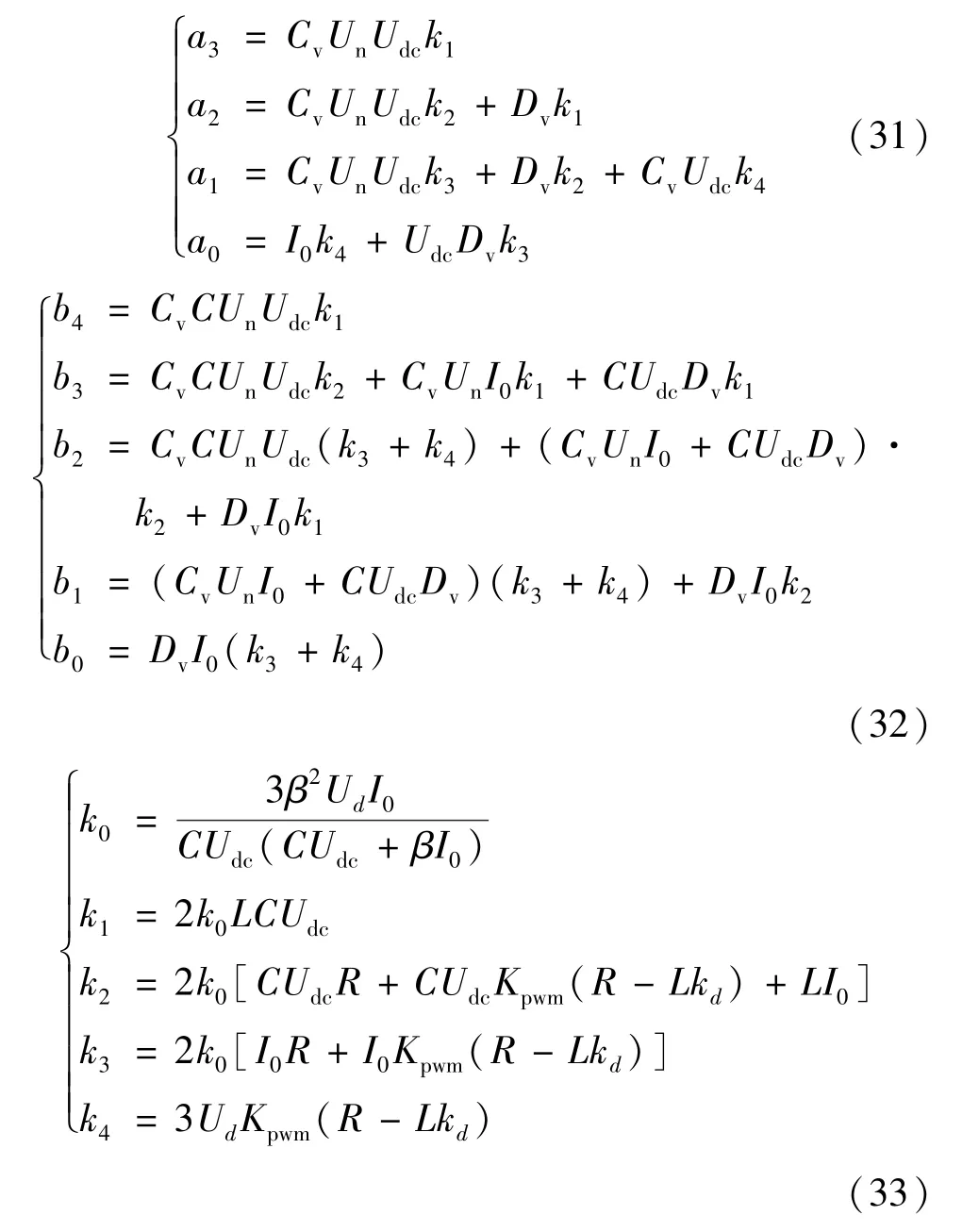
为分析所提控制策略下系统的稳定性,根据式(30)绘制出BGC 闭环控制系统的Nyquist 曲线,如图6 所示。 其中,图6(a)为不同虚拟电容Cv下系统的Nyquist 曲线图,图6(b)为不同阻尼系数Dv下系统的Nyquist 曲线图。
从图6 中可以看出在多滑模控制算法下BGC 系统的Nyquist 曲线不包围( -1,0)点且距其有较远的距离,系统维持稳定。 且当虚拟惯量Cv和Dv在一定范围内变化时,系统仍具有良好的稳定性。
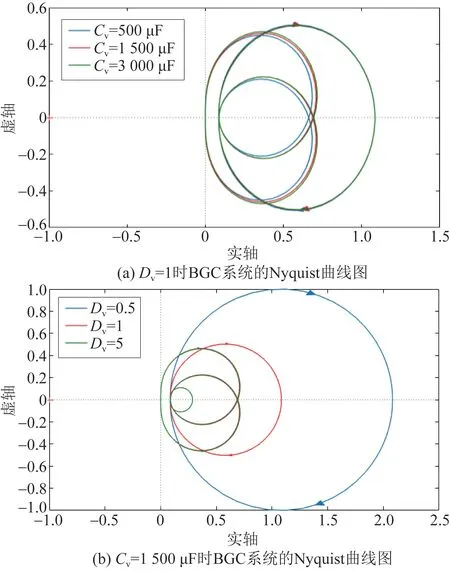
图6 BGC 系统的Nyquist 曲线图Fig.6 Nyquist curve of BGC system
4 仿真分析
为验证所提控制策略的有效性,在Simulink 中搭建了图2 所示的BGC 系统仿真模型,系统仿真参数见表1。 本文在PI 参数选取上参照典型二阶系统的整定方法,通过仿真调试综合考虑比例及积分系数对暂态波动及恢复速度的影响,选取动态性能较佳的一组参数。 无源控制注入阻尼参数的选取同样存在波动幅值与响应速度的矛盾,注入阻尼较小时,电压波动大但响应速度快;注入阻尼较大时,电压波动小但响应速度慢。 因此,经仿真调试,无源阻尼参数也遵循动态性能较佳这一选取原则。
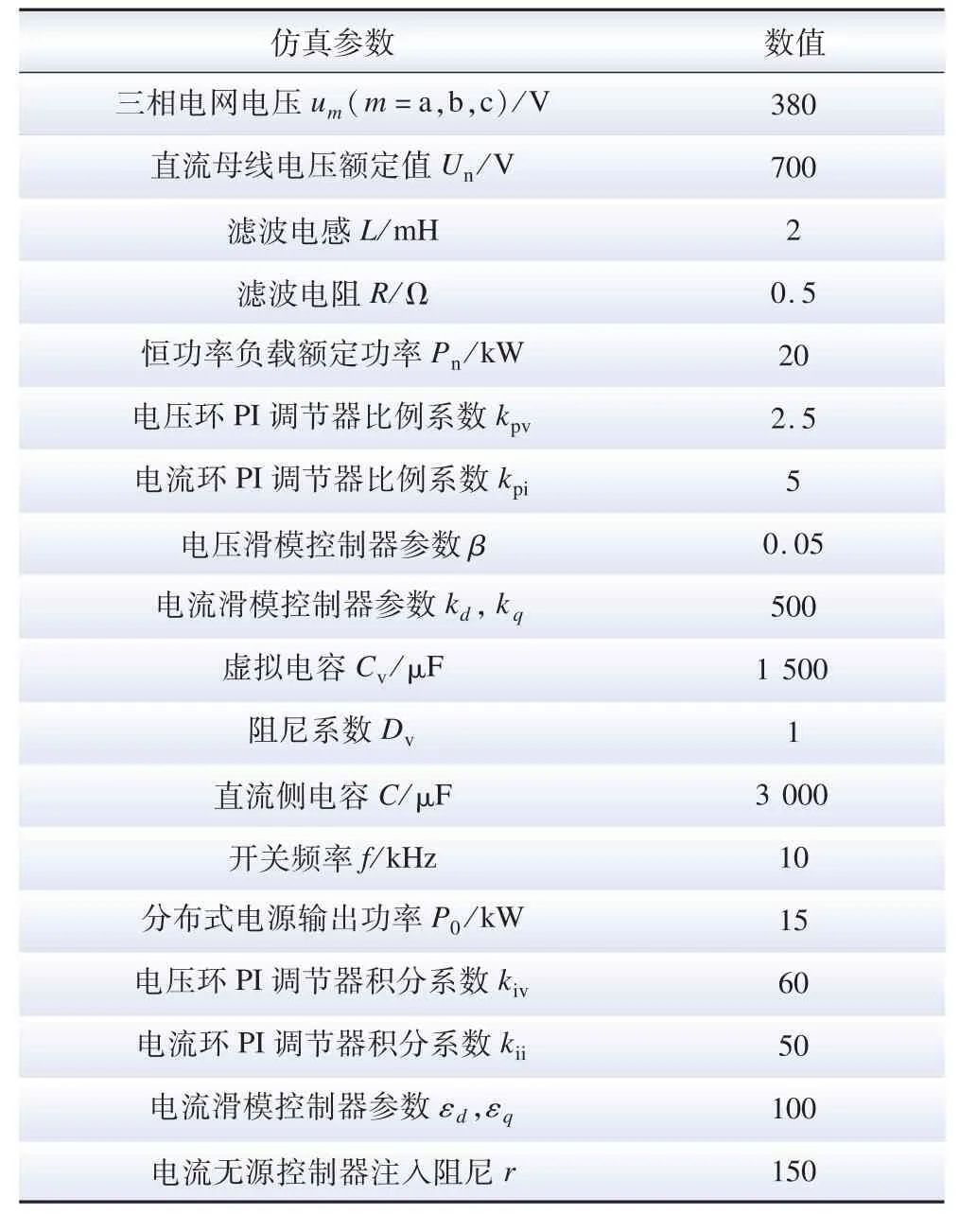
表1 BGC 系统仿真参数Table 1 Simulation parameters of BGC system
将本文所提基于多滑模控制的VIC 策略与基于PI 控制、无源控制的VIC 策略进行仿真对比,三种控制策略下BGC 直流侧母线电压的动态响应和网侧电流的电能质量分析如图7 和图8 所示。 设定BGC 工作在整流状态下传输功率P为正值,逆变状态下传输功率P为负值,给出如下2 种案例。
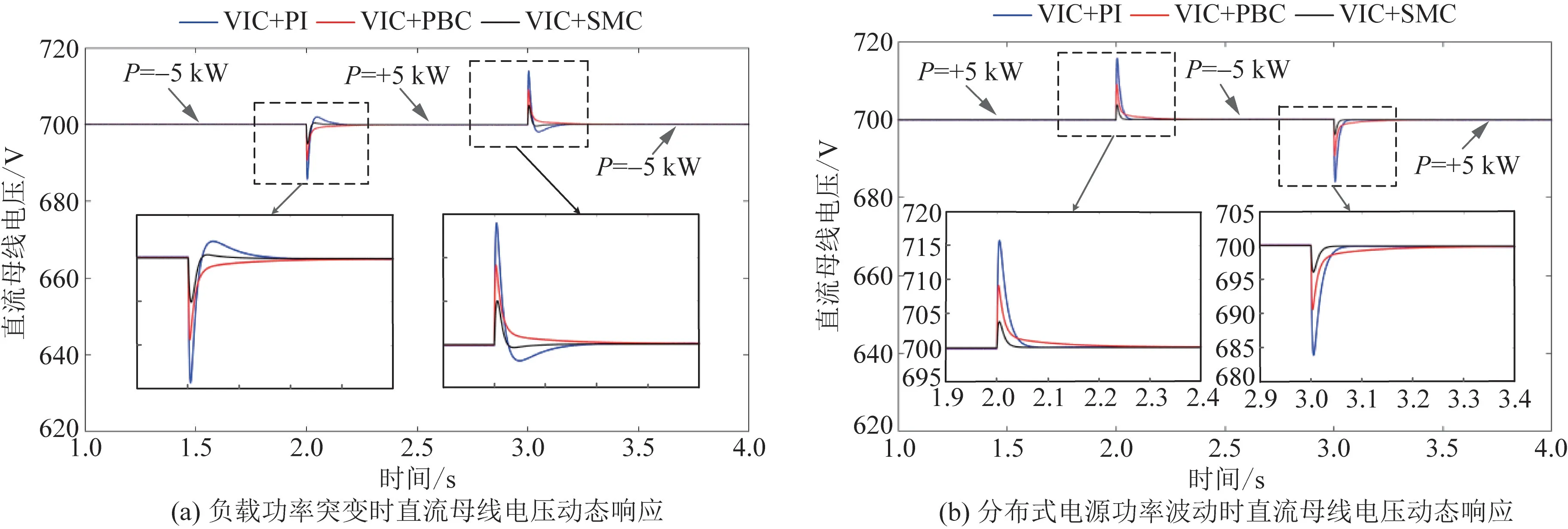
图7 三种控制策略下直流母线电压对比Fig.7 Comparison of DC bus voltage under three control strategies
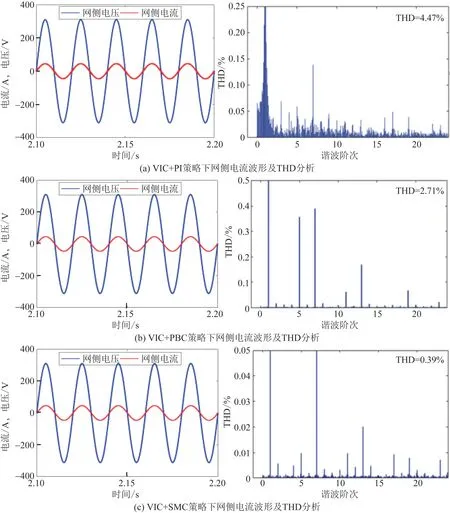
图8 三种控制策略下网侧电流波形及THD 分析Fig.8 Waveforms of grid-connected current and THD analysis under three control strategies
仿真案例1:研究恒功率负载功率突变对直流母线电压的影响。 直流侧分布式电源输出额定功率为15 kW,2.0 s 时负载功率由初始功率10 kW 突增为20 kW,3.0 s 时负载功率又突减为10 kW。
仿真案例2:研究分布式电源功率波动对直流母线电压的影响。 设定恒功率负载额定功率为20 kW,分布式电源输出功率在2.0 s 时由初始功率15 kW突增为25 kW,在3.0 s 时又突减为15 kW。
表2 给出的三种BGC 控制策略分别为基于PI控制的虚拟惯性控制(virtual inertia control, VIC),基于无源控制(passivity-based control, PBC)的虚拟惯性控制,以及本文所提出的基于多滑模变结构控制(sliding mode control, SMC)的虚拟惯性控制策略。

表2 三种控制策略下直流母线电压动态性能指标Table 2 Transient performance index of DC bus voltage under three control strategies
由图7 及表2 的数据可知,经不同仿真案例分析对比,采用基于多滑模变结构的VIC 策略与基于PI控制、无源控制的VIC 策略相比,直流母线电压暂态波动的幅值最小,同时母线电压恢复到稳态所需时间也最短,在三种控制策略中动态性能最优。
由图8 可知,三种控制策略均实现了网侧电压、电流单位功率因数控制这一目标。 根据总谐波失真(total harmonic distortion,THD)分析可知,与PI控制和无源控制相比,多滑模变结构控制下网侧电流总谐波畸变率更低,更好地保证了BGC 网侧电能质量。
图9 为在本文所提VIC +SMC 控制策略下设定不同虚拟电容Cv时直流母线电压的动态响应对比。由图9 可知,在BGC 虚拟惯性控制环节,随着虚拟电容Cv的增大,母线电压的暂态波动幅值逐渐减小,直流微网的惯性得到增强。 但较大的虚拟电容Cv会延长母线电压恢复到稳态的时间,使系统的动态响应速度变慢。 因此需根据实际控制需求选取合适的虚拟电容值。
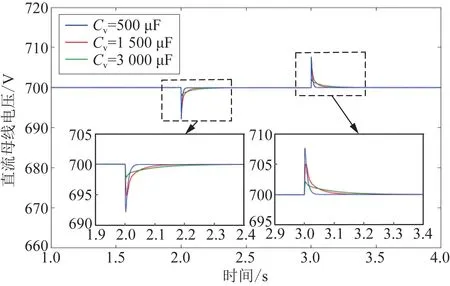
图9 不同Cv下的直流母线电压动态响应Fig.9 Dynamic response of DC bus voltage under different Cv
上述结果验证了本文所提基于多滑模变结构的VIC 策略能够在负载功率突变及分布式电源波动时有效抑制直流母线电压大幅波动,增强直流微网的惯性,使BGC 系统具有较好的动、静态性能。
5 实验验证
为进一步验证本文所提控制策略的有效性,搭建的由StarSim HIL 控制的BGC 系统的硬件在环实验平台如图10 所示,实验参数与仿真相同。 图11 给出了负载功率突变下采用基于PI 控制和多滑模控制的VIC 策略的直流母线电压对比及不同虚拟电容下直流母线电压的动态响应波形。

图10 基于StarSim HIL 的BGC 系统实验平台Fig.10 Experimental platform of BGC system based on StarSim HIL
图11(a)—(c)给出的电压局部放大图中,纵坐标每小格电压值为2 V,横坐标每小格时间间隔为40 ms。从图中对比可以看出,本文提出的基于多滑模变结构(SMC)的VIC 策略与基于PI 控制的传统VIC 策略相比,暂态下直流母线电压的波动幅值更小,母线电压恢复到稳态的时间更短,提高了BGC 的动态性能。 同时,选取不同的虚拟电容值,随着Cv的增大,母线电压波动幅值进一步减小,但同时会延缓系统的动态响应速度。
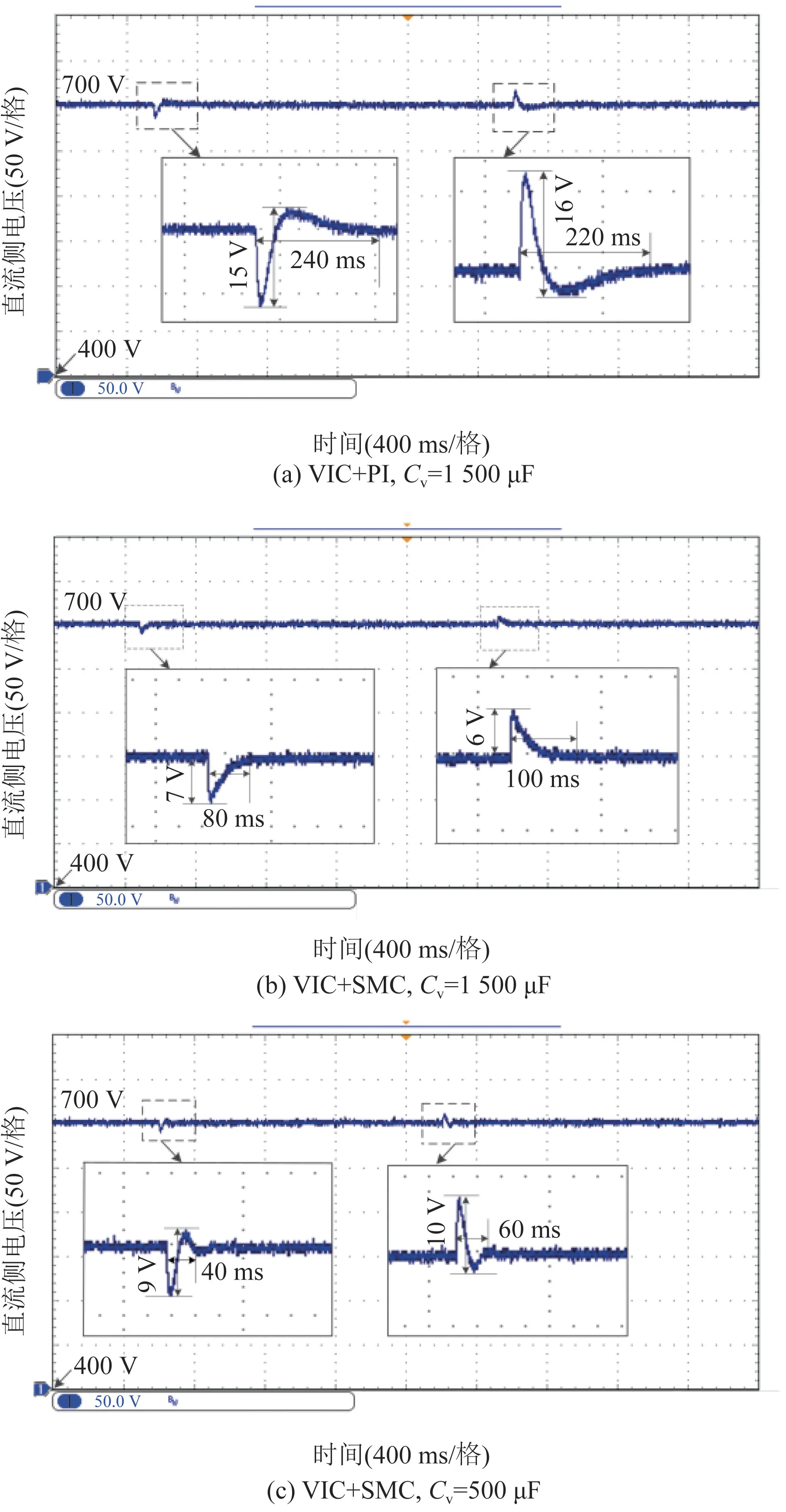
图11 负载功率突变时直流母线电压的实验波形Fig.11 Experimental waveforms of DC bus voltage when load power suddenly changes
图12 给出了采用基于PI 控制和多滑模控制的VIC 策略下BGC 的网侧电压和电流波形。 由图12可知,本文所提控制策略与基于PI 控制的VIC 策略相比,并网电流总谐波畸变率更小, 更好地保证了BGC 交流侧的电能质量。
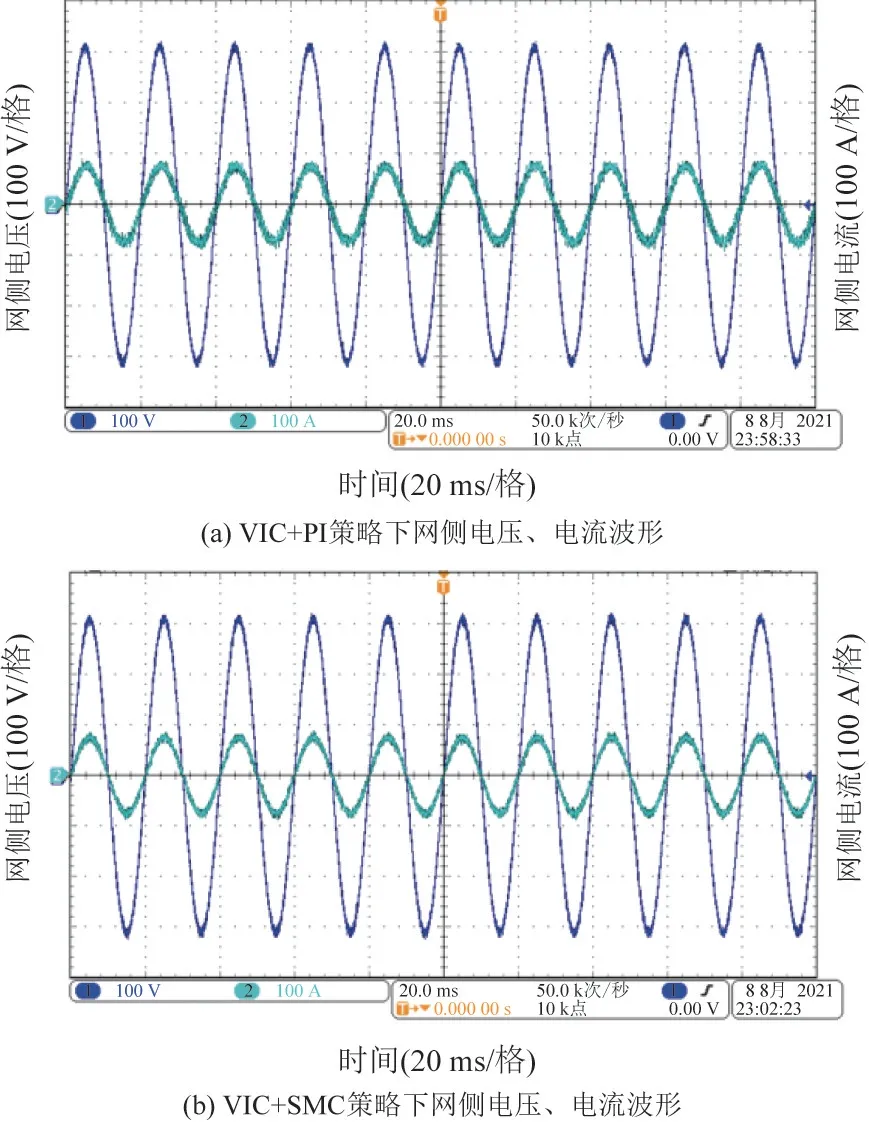
图12 不同策略下网侧电压、电流的实验波形Fig.12 Experimental waveforms of voltage and current at network side under different control strategies
6 结论
为提高暂态下BGC 的控制性能,抑制负载扰动下直流母线电压的大幅波动,本文在传统VIC 策略的基础上进行改进,提出基于多滑模变结构控制的VIC 策略,得到以下结论:
1)内环采用基于指数趋近律的滑模电流控制,实现了对并网电流给定值的快速跟踪,提高系统响应速度的同时抑制了并网电流谐波畸变;
2)外环建立虚拟惯性方程与滑模电压控制,增强直流微网的惯性,有效抑制了直流母线电压波动。
本文通过引入多滑模控制算法提升了BGC 系统的动、静态性能,但虚拟惯性环节的参数Cv仍对母线电压有较大影响。 文中虚拟电容Cv为固定值,无法兼顾系统的惯性和响应速度,下一步可针对参数Cv设计自适应调节算法,并研究其稳定边界。
