基于Shepard 插值残差修正的TIN 模型预测高程异常

赵春艳

（1. 唐山市水利规划设计研究院，河北 唐山063000）

随着卫星定位技术的发展，高程测量方法由传统的水准测量逐渐向GNSS测量转变。如何实现大地高转化为正常高是相关工作人员的研究热点[1-3]。目前常见的数学模型有二次曲面模型、多面函数模型、最小二乘配置模型和半参数模型等，配合常用的重力场模型例如EGM96、EGM2008、EIGEN-CG01C，可以获取厘米级的高程异常拟合成果，但上述数学模型均是在一定区域内构建总体模型，待定点计算的高程异常成果仅与其坐标值有关，未能与临近已知点产生关联[4-12]。针对上述问题，移动曲面模型可以根据待定点与已知点的距离定权进行拟合，但精度未有明显提高，考虑到狄洛尼三角网（TIN）能够对测区进行细化，本文使用TIN模型进行高程异常拟合计算，针对靠近三角形边界的待定点，加入Shepard插值进行残差修正。

1 高程异常的TIN模型

狄洛尼三角网是相互连接但互不重叠的三角形的集合，各三角形的外接圆均不包含其他点，建网时的步骤为：选取最西南方向一点作为起始点，与相邻一点形成基边；然后寻找第三点形成三角形；再以新生成的两条边分别作为基边，继续构建三角形，构建时应当满足各三角形的外接圆均不包含其他点的条件。

在高程异常拟合中，狄洛尼三角网应当以已知点作为三角形顶点，布网结束后应确保所有待定点有且仅有一个所属三角形。此时各待定点的高程异常值与其所属区域有关，也与所属区域顶点的高程异常值有关，可取待定点到三角形顶点的距离定权，则高程异常的TIN模型待定点高程异常计算公式如式（1）所示：

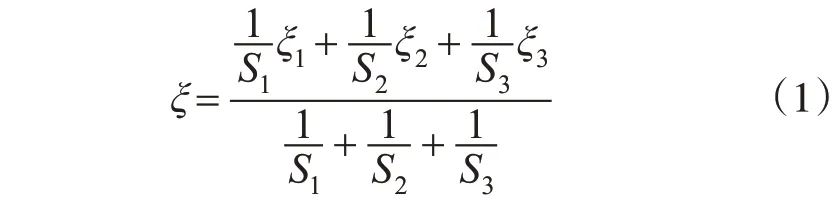
式中，ξ为待定点高程异常值；S1,S2,S3为待定点至顶点的距离；ξ1,ξ2,ξ3为顶点的高程异常值。

如上文所述，高程异常的TIN 模型存在待定点处于边界时的不确定问题，因为TIN模型是根据待定点所属区域确定其高程异常值，若待定点处于边界附近，其与本区域的相关性就会降低，与邻近区域的相关性提高，在式（1）中体现的就是待定点至顶点的距离明显增加，导致高程异常值结果精度降低。针对此问题，考虑到Shepard 插值也是根据待定点与已知点的距离进行拟合，因此使用Shepard 插值对处在边界上的待定点进行残差修正。

2 基于Shepard插值残差修正

Shepard插值的计算式如式（2）所示：

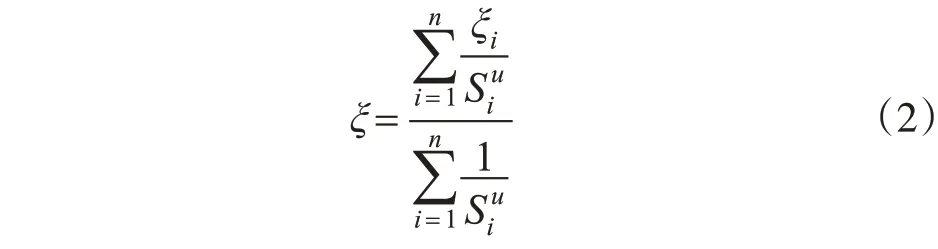
式中，n为使用的已知点的个数；ξi为已知点高程异常值；为待定点至已知点的距离的u次方，一般取2。

由式（2）可以看出，当n=3,u=1 且ξi与Si均取三角形顶点时，Shepard 插值就转化为高程异常的TIN模型，即TIN模型是Shepard插值的一种局域化形式。通过限定Shepard 插值的参数达到根据待定点所属区域确定其高程异常值的目的，但待定点存在处于三角形边界的情况，且即使待定点处于三角形内部，只要待定点与三角形边界距离足够近，也会引起精度降低，因此本文提出基于Shepard 插值残差修正方法，具体步骤如下：

当判断待定点处在三角形边界或邻近边界时，将邻近边界所在的三角形与待定点所在三角形拼接为四边形，根据式（2）将四边形的边界作为已知点进行待定点高程异常值计算，即式（2）中n=4，u的取值由2～4 进行调整，以获取最优的次数取值。通过基于Shepard 插值残差修正方法，预期将处在三角形边附近的待定点在四边形内进行高程异常值拟合，以克服此类待定点精度较低的问题，下面将结合实例计算对本文提及的理论进行验证。

3 工程概况

实验数据选取文献[13]中表1的数据，GNSS控制点共计24 个，选取其中的HM01、MH02、HM09、MH12、MH20 作为待定点，其余19 个点作为已知点，点位分布如图1所示，其中红色点表示待定点，黑色点表示已知点。X坐标由3 063 483.914～3 076 071.229 m；Y坐标由524 279.238～536 033.195 m；高程异常值由-19.226～18.999 m。根据狄洛尼三角网的划分原则，将图1 中的区域划分为狄洛尼三角网。如图2 所示，其中蓝色标记区域为待定点区域，红色标记区域为无待定点区域，下一步拟合值计算主要针对蓝色标记区域进行，蓝色标记区域编号为：W，X，Y和Z，其中W 区域待定点为MH20，X 区域待定点为HM01 和MH12，Y区域待定点为MH02，Z区域待定点为HM09。

图1 点位分布

图2 狄洛尼三角网划分

4 TIN模型实例验证

各待定点区域的三角形边界点如表1 所示，由于图2 中可以看出HM01 处在邻近边界上，其点位标记已与边界线重合，因此将XK 的联合区域也作为待定点区域，以便后续使用Shepard插值进行残差修正。

表1 三角形边界点

使用TIN模型中式（1）对待定点进行高程异常值计算，同时为方便比较，使用二次曲面拟合模型对待定点也进行计算，计算成果如表2所示。

表2 二次曲面与TIN对比/m

对比真误差，W 区域的MH20 与X 区域的MH12在TIN模型中有明显的真误差减小，由3 cm以上降低到2 cm以下，Y区域的MH02和Z区域的HM09在TIN模型中真误差降低一个数量级，由厘米级降低为毫米级。观察图2 中的区域划分，可知以上4 点均未与三角形边界点重合，虽然W 区域的MH20 与Y 区域的MH02 点位与边界线邻近，但点位标记存在一定的半径，实际点位与边界线仍有一定的距离；X 区域的HM01 其点位标记与边界线出现重合，导致其TIN 模型的拟合精度相对于二次曲面反而降低，说明在该点拟合中，二次曲面的整体拟合效果优于TIN模型的局部拟合效果，因此该点所在区域的局部选取存在不足，需要对其进行残差修正。

5 Shepard插值残差修正实例验证

以上内容验证了TIN 模型中存在的弊端，针对此问题结合本文的理论基础，将HM01在XK区域内进行重新计算，计算时对距离u的次数分别取2，3，4，计算成果如表3所示。

表3 HM01点Shepard插值残差修正/m

当u的次数增加时，Shepard插值的真误差逐渐减小，在u=4 时降至亚mm级，说明本文使用的Shepard插值的残差修正对TIN模型的边界点有较好的真误差修复效果，将待定点在边界线上的情形转化为邻近三角形拼接，在四边形中进行Shepard 插值计算更符合该种待定点的特性，修复后的TIN 模型与未修复的TIN模型、二次曲面模型对比曲线如图3所示。

图3 真误差对比

计算3种模型的平均相对误差如表4所示。

表4 平均相对误差对比

本次实例计算中，选取区域较小，因此待定点数量有限，改进的TIN模型精度提升不明显，若在大区域中使用本文的方法，则随着边界线上的待定点增加，改进的TIN模型的效果会逐渐增大；在未进行改进时，TIN 模型也优于常规的二次曲面拟合模型。需要注意的是，TIN模型在计算前需要进行三角网划分，使得该方法在大区域拟合中会降低计算效果，因此应当权衡精度与成本，选取合适的高程异常拟合模型。

6 结 论

本文由TIN 模型入手，验证了其在高程异常拟合中相较于常规模型的优势，针对该模型存在的缺陷，结合与之原理近似的Shepard 插值法进行了残差修正，结果表明Shepard插值法能有效克服TIN模型中待定点处于边界线上的缺陷；Shepard插值法随着其距离次数u的增长，真误差逐渐减小；待定点使用改进后的TIN模型后真误差由0.019 52 m降低为0.000 7 m，最终平距相对误差为0.036%，由于常规二次曲面的0.124%与未改进的TIN模型的0.055%。在实际使用中应注意，实际点位划分很难严格遵循狄洛尼三角网的划分原则，如何寻找一种更优的三角形划分方法，是下一步研究的重点。