球坐标多面函数对大区域数据插值的应用研究

孟 涛,孟祥恩,曾现敏,马治忠*,吴啸龙

（1. 国家海洋局北海海洋技术保障中心，山东 青岛 266033；2. 西安科技大学，陕西 西安 710054）

目前大地测量学领域主要采用的观测手段是空间大地测量观测技术，该技术打破了以往经典大地测量的时空局限性，从而实现精确、直接、全面的在超大尺度乃至全球尺度上的大地测量监测数据采集，而研究基于球坐标多面函数的空间数据插值方法也是为了适应这一技术带来的变化[1-4]。

1 球坐标多面函数观测方程

多面函数在笛卡尔坐标系中的数学形式可表示为[5]：

式中，n为参与多面函数建模的已知节点数；Q(X,Y,Xj,Yj)为多面函数模型的核函数；αj为多面函数待定系数。

一种常用多面函数的双曲型核函数形式为：

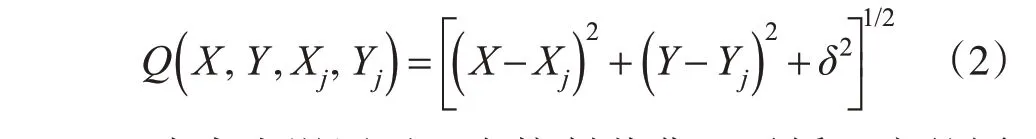
上式中光滑因子δ在控制着曲面平缓程度的同时，在其几何意义上还表示这曲面上最小值点到X-Y坐标平面的距离，即δ2=(z-zj)2。在几何上该参数也可以视为不同半径的两个同心球层在同一点处的半径差异[6]。因此，在笛卡尔坐标系下，结合笛卡尔平面坐标和球坐标之间的转换关系，式（2）可以写为如下形式：

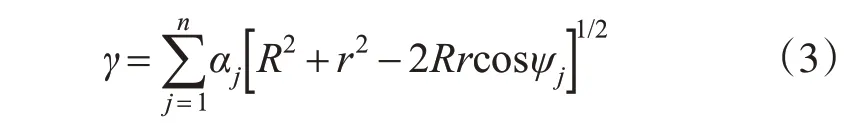
其中，

式中，R为地球球状模型的平均曲率半径；r 为最优内部球层半径常数；θ为余纬度；λ为经度。

式（3）中的r 为针对某一研究区域（范围）最优的内部球层常半径，Hardy 等给出了最优半径迭代公式为：

式（6），（7）分别对应为全球尺度下、局部地区的第一辅助方程；式（8）为第二辅助方程；n为研究区域内用于多面函数建模的已知观测数据个数；A为用于建立多面函数模型的已知数据所覆盖区域的球面面积。由式（5）～（8）可知，当给定分布在球面上的建模数据点的个数n以及地球平均曲率半径后，可以得到针对当前已知数据分布情况的最优r 解析式。然而，式（5）为无显式解的隐函数，需要根据二分法求解当前已知结点分布水平对应的内球层最优半径。

经过坐标变换后，基本的多面函数模型仍可以表达为线性结构。在实验范围内，对n个实测点选取m个点数据（m≤n），构建出多面函数模型式（9），其在最小二乘算法下的最优解如式（10）～（13）所示[7～9]：

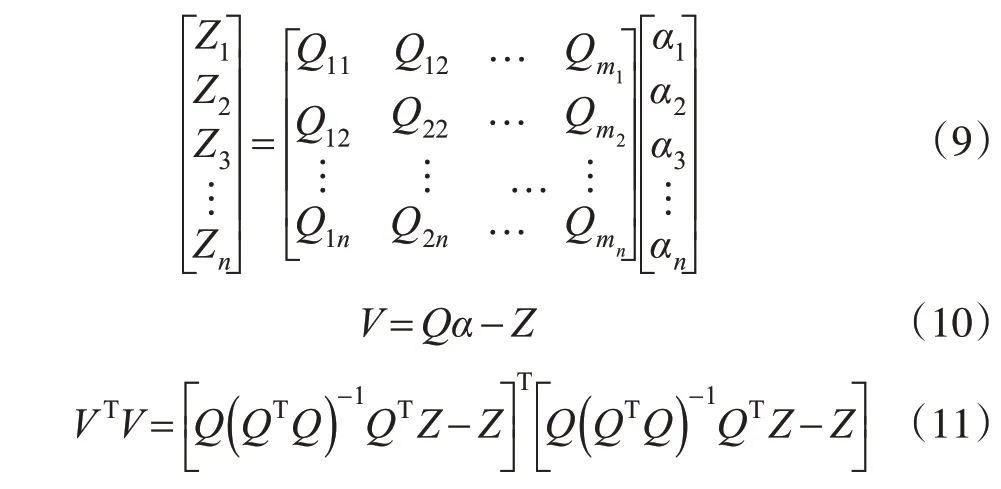
假定已知n个采样点上的地壳垂直运动速率和位置，并确定了核函数的具体形式，则速率面拟合就是依据n个采样点的速率观测值求解一组待定参数。

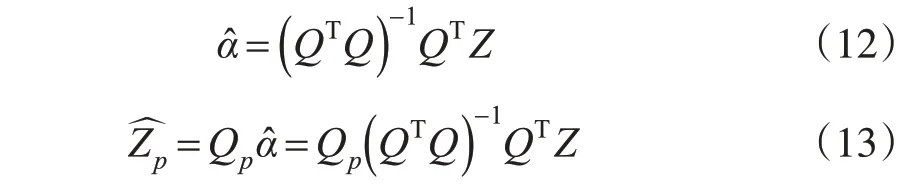
当m=n时，

2 算例与分析

2.1 算例1

本算例旨在验证球坐标系下多面函数模型对于大、中尺度空间离散数据插值应用的可行性及其精确程度。研究范围选取为120°～135°E，18°～28°N 的843 个已知点大地水准面高程数据。选取其中分布均匀的94个点作为外部检查点，用于评定所建立模型的拟合精度。研究分别采用不同数目的已知数据构建数学模型，计算并评价球坐标系和笛卡尔坐标系下多面函数的拟合精度；球坐标多面函数与其他空间数据插值算法的拟合精度。

外部检查点均方根误差计算公式[10-11]为：

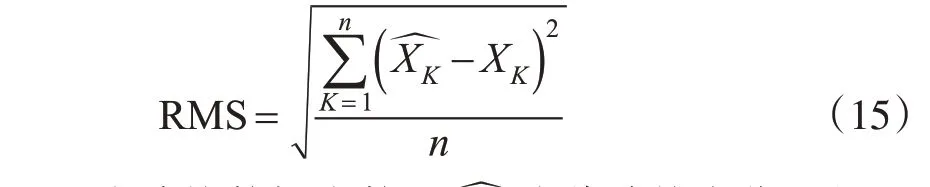
式中，n为检核数据个数；XK为待检核点位置的已知量；XK为待检核点位置的模型拟合结果。

本文分别给出了起算结点个数为843,281,211,169,141,121,106时，在球坐标系与笛卡尔坐标系的多面函数中，对外部检核点的均方根误差分别进行计算，结果走势如图1 所示。三角形符号表示球坐标多面函数的建模结果，星形符号表示笛卡尔平面坐标多面函数的建模结果。从图中可以看出，随着用于建立多面函数模型的已知结点数目的减少，多面函数计算外部检核点的精度逐渐变差，其均方根误差在球坐标多面函数中建模结果的变化幅度要显著小于笛卡尔坐标系的结果。

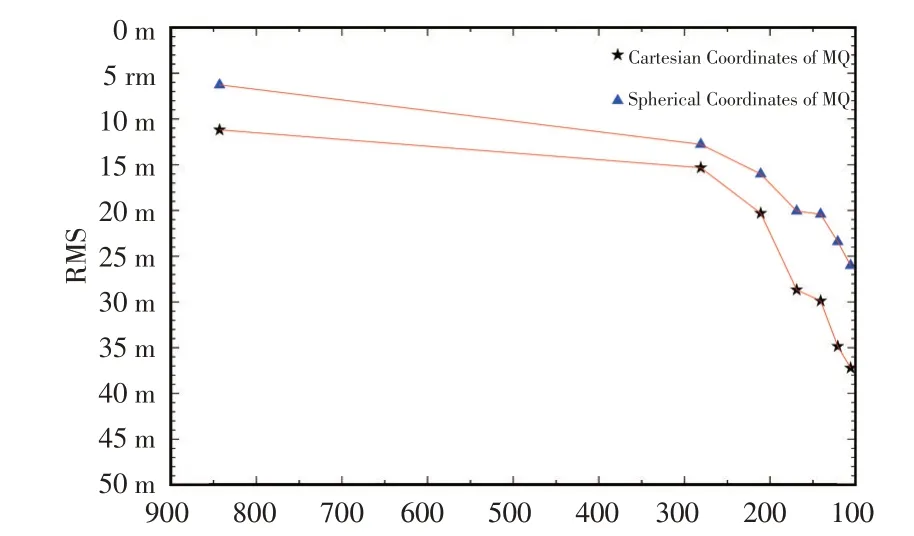
图1 不同坐标系统的多面函数建模均方根误差变化趋势对比

不同方案建模结果精度评定的详细统计结果见表1，结合图1 所示趋势与表1 中的拟合残差统计结果可知，多面函数在球坐标系下相较于笛卡尔坐标系的建模结果，对于离散点的稳定性以及拟合精度更优。

表1 不同方案拟合残差统计/m

为了进一步研究大、中空间尺度下球坐标系多面函数的插值精度，本文对同一组已知数据，分别采用局部多项式法、最邻近点法、克里格法、改进谢别德法等算法对研究区域内的250 个外部检核点进行建模拟合[12-14]，其拟合残差分布如图2所示，红色曲线为球坐标多面函数对外部检核点的拟合残差分布。由此可知，在研究区域内部，球多面函数对于空间数据的插值精度达到甚至优于一些常规算法。

图2 不同算法的外部检核点拟合残差对比

2.2 算例2

水准数据是典型空间大地测量离散的观测结果，采用动态平差方法获得的区域地表垂直运动信息在时间域、空间域方面是不连续的[15-16]。实际上，地面垂直运动表现为地表上连续形状变化的曲面，各水准点则是这个曲面上的离散采样结果。为实现在时间域、空间域中的连续性垂直变化信息，多面函数被广泛应用于给予离散数据获取连续形变速率面的研究当中。

然而，两点高差为水准测量的直接观测量，利用水准观测量平差得到的水准速率仅有相对意义，所以必须确定参考基准。不同参考基准的选择可能获得完全不同趋势的形变速率场。因此，在根据水准数据判断区域地面变化的稳定性时，常常引入垂直速率梯度。垂直运动高梯度带及速率等值线的急剧转折部位往往是地面构造薄弱、易失稳区域。

梯度作为一个向量，依据定义，地壳垂直运动速率梯度应为相应坐标分量的偏导数。黄立人等曾基于笛卡尔坐标系下多面函数模型给出了垂直速率在N方向和E方向的偏导数分量计算模型，并针对地震高危区域进行了深入研究，取得了大量有益结果。然而，地面垂直形变速率场的径向梯度对于区域地面构造稳定性的判定、指向特性还有待进一步研究。

根据Hardy与Gopfert[4]，任何由式（3）、（4）进一步推导得到的函数关系仍然为线性模型。在利用球多面函数理论构建区域垂直速率面模型的基础上，可以进一步求解其速率在径向的梯度分量。假设式（3）表示垂直形变速率面，则其对径向坐标分量R的偏导数可以按照下式进行计算：

式中，先验参数r和ψj可以由式（4）、（5）进行计算。

为了便于验证该模型的客观性与正确性性，本文选取分布在福建省的水准垂直速率场数据资料，利用式（16）计算出研究区域地面垂直形变速率径向梯度分布，其结果如图3所示。

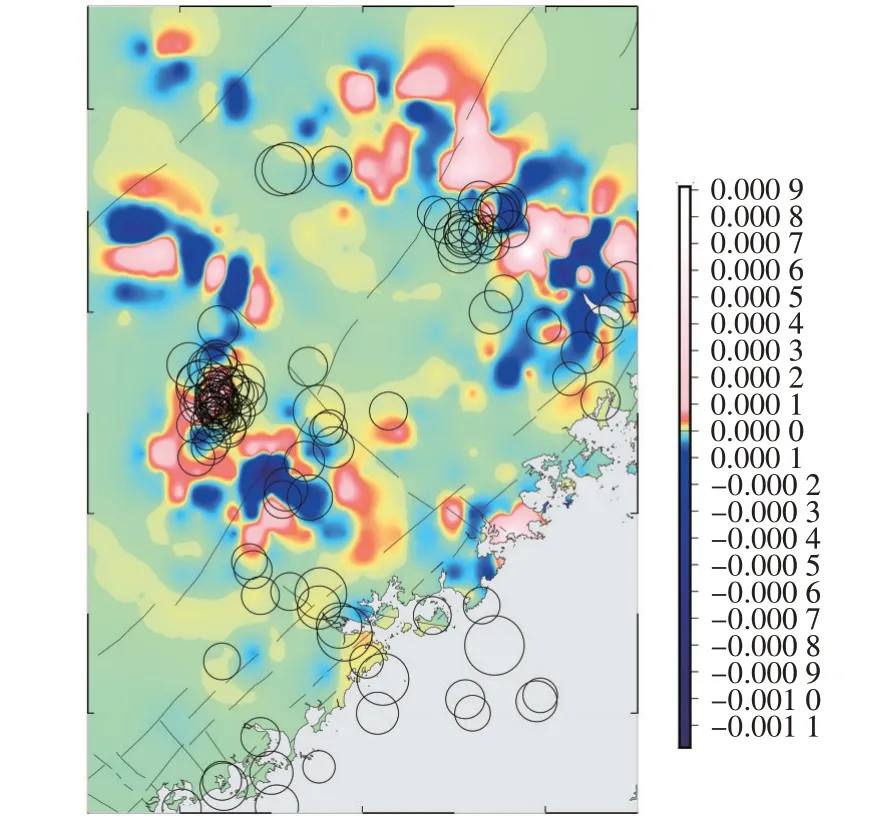
图3 径向梯度分布

从图3 中可以看出，地面垂直形变速率场的径向梯度分布规律与区域内的重大活动构造（地壳的薄弱区域）具有良好的相关性。福建省东南沿海地壳地震活动主要受控于北东向的断裂系，及与其正交的北西断裂系的共同作用[17]。从径向梯度带的密集变化区域分布可以看出，高梯度带地区与历史地震分布具有良好的空间相关性。也就是说，断裂带的交汇部位，径向梯度分布密集变化剧烈，对应的地震时间分布频度高。

3 结 语

根据本文研究，可以得到以下几点结论：

1）从正双曲型核函数的几何意义出发，同时控制着正双曲面的平缓程度以及曲面上所有点到x-y坐标平面的最小距离。因此，可以将视为两点z坐标分量的差异，从而最终获得球坐标系下多面函数的基本模型。

2）为了进一步分析球坐标多面函数对大、中尺度上的球多面函数的拟合精度，本文选取分布在我国东南部范围为120°～135°E，18°～28°N的大地水准面离散数据进行插值精度分析。通过计算球坐标多面函数与笛卡尔平面坐标多面函数在不同建模方案下的整体拟合残差以及均方根误差，本文研究认为针对较大矩形区域内的离散数据，采用球坐标系多面函数的得到的数据插值精度与稳定性均优于相比于笛卡尔坐标系的计算结果。另一方面，本文进一步对比了球多面函数与几种常见空间数据插值模型的插值精度，结果显示本文模型相对于其他算法，精确度与稳定性都较好。

3）由于水准测量结果仅具有相对意义，难以单纯地依靠速率值大小来衡量地壳运动的稳定性。因此常将地壳运动的垂直运动高梯度带，及其等值线的急剧转折部位作为未来区域地面差异性变化或构造应力显著作用区的判断依据。本文在球坐标系多面函数拟合垂直速率面的基础上，进一步推导了垂直速率的径向梯度分量。并选取福建省东南沿海地区的垂直速率观测数据进行径向梯度分布的解算。结果显示判定垂直速率的径向梯度分布与地壳构造薄弱、易失稳的区域就有良好的空间对应关系。因此，该研究方法在理论上同样适用于矿山采空区地面沉降监测及相关地质灾害、危险区区划等工作的研究。