动态无线充电下电气化交通网-配电网运行机理与协同优化

刘健辰，张淏源，刘傲阳，曹诗琪

（辽宁工程技术大学电气与控制工程学院，辽宁省葫芦岛市 125105）

0 引言

交通运输在整体能源消耗中占有很大比例，电气化交通不仅是能源革命、能源转型的组成部分，更是实现碳达峰、碳中和目标的重要途径［1-3］。其中，电动汽车（EV）的动态无线充电（dynamic wireless charging，DWC）也称为途中充电，可通过非电气接触方式实现电能传递，避免了传统充电方式易漏电、接触损耗等弊端，为行驶状态的EV 实时传输电能［4］，从而缓解里程焦虑，缩小电池体积，应用前景广阔［5-8］。

EV 的日益普及使得交通网和配电网之间产生密切而复杂的耦合关系，大量EV 的充电行为会对交通网与配电网产生双向影响［9-11］。在配电网侧，EV 的无序充电可能引发区域配电容量不足、电压跌落和频率降低等问题［12］；在交通网侧，EV 用户的潮汐特征导致各个充电站车辆分布不平衡，供给与需求不匹配［13］。而在引入充电电价和道路收费的调控手段后，必须考虑交通网- 配电网（transportation-distribution networks，T-DN）之间的相互依赖性［14］。文献［15-16］提出了可描述电力与交通需求变化的多时段综合定价模型，并揭示了无导向交通流可能会增加电网中不安全运行的风险。但是，目前的研究缺乏对电气化T-DN 的综合建模，特别是在DWC 环境下的短期T-DN 协同优化。

分析DWC 下的T-DN 联合运行机制的核心是确定EV 充电负荷的动态时空分布。目前，绝大多数文献采用静态配流（static traffic assignment，STA）方法分析EV 充电负荷的时空分布［17-18］，无法反映短期（3～15 min）交通流时空分布的动态变化［19］。近年来，研究者尝试采用半动态配流（semidynamic traffic assignment，SDTA）方法［20-21］和动态配流（dynamic traffic assignment，DTA）方法研究EV 交通流和充电负荷的中期（60 min）或短期动态时空分布［22-23］。文献［20］发现，交通高峰时段T-DN中的负荷可能发生时空重叠，导致路-电双网拥堵-拥塞程度进一步加剧。文献［24］指出，STA 和SDTA 方法对时间信息进行了忽略与简化处理，导致配流结果严重偏离实际情况，并且计算误差会随着交通网拥堵程度的增加而更加严重。因此，亟须采用适于短时配流计算的DTA 方法进行EV 充电负荷的动态时空分布分析。

主动配电网中包含大量分布式电源［25-26］、无功补偿装置［27-28］和储能装置［29］，可以为电气化T-DN的经济安全和低碳运行提供有功、无功灵活性电源。但是，分布式电源的大规模并网可能造成电压越限和逆向潮流，增加了电网调控的难度［30-32］。

基于以上考虑，本文首先建立DWC 环境下的电气化T-DN 联合运行模型，并参考文献［33-34］，引入变分不等式理论分析混合动态用户均衡（dynamic user equilibrium，DUE）状态，完成DTA 计算。然后，通过大量仿真算例，揭示了深度耦合下混合车流的时空演化现象，并据此分析了路-电双网中拥堵-拥塞的连锁性产生机理。最后，提出基于主动配电网的有功-无功协同优化措施，以达到缓和或消除路-电双网中不良连锁性拥堵-拥塞的目的，并研究了合理配置有功、无功电源容量对协调优化效果的影响。

1 T-DN 联合运行系统

基于DWC 技术的电气化T-DN 的基本结构如图1 所示，包含3 个部分：电气化交通网、主动配电网和耦合单元。

图1 电气化T-DN 结构Fig.1 Structure of electrified T-DN

电气化交通网内的道路上存在由EV 和其他燃油汽车（gasoline vehicle，GV）构成的混合车流。EV在经过充电道路时，通过DWC 技术进行充电，这种集中式的动态充电行为通过无线充电站接入配电网的相应节点。主动配电网包含光伏电站、无功补偿装置、储能装置等多种有功、无功电源。

无线充电站作为耦合单元，实现了交通网与配电网之间的交互影响。一方面，交通网中的EV 受到EV/GV 混合车流的影响，形成了充电负荷的时空分布，进而通过无线充电站改变了配电网中的潮流分布；另一方面，EV 充电负荷会通过无线充电站改变配电网中的潮流分布，进而通过节点电价或拥塞成本影响EV 驾驶者出发时间和行驶路径的选择，从而反向影响交通网中的车流分布。这就是TDN 中的“双向影响”。

需要指出的是，交通网中无线充电路段的交通拥堵，会通过无线充电站与配电网中的其他用电负荷高峰叠加，可能造成节点电压越限，即配电网拥塞。而为了消除配电网拥塞而设立的充电拥塞成本，会反过来影响交通网中的车流分布，造成原来没有拥堵的路段产生新的拥堵，从而形成T-DN 中的连锁性拥堵-拥塞问题。

2 T-DN 联合运行模型及求解

本章在图1 所示各个环节动态模型的基础上，建立T-DN 联合运行模型，进而提出求解方法。

2.1 交通网的DUE 模型

在采用DWC 技术的环境下，道路拥堵状况和充电费用会影响EV 交通流的时空变化，进而影响充电负荷的时空分布，为T-DN 的协同运行奠定了基础。假设一个交通网包含起止点（O-D）对（o，d）的集合为W，其中，o为起始点，d为终点。O-D 对可以包含多条路径p∈Pod，其中Pod为路径集合。

假设在DTA 情况下，所有交通网内的出行者共同参与一个具有出发时间和行驶路线双自由度选择的非合作Nash 博弈［34］，动态交通流最终达到DUE 状态［35］，即相同出行目的的所有用户具有相同的综合出行成本。基于流体动力学中的Lighthill-Whitham-Richards 模型［36］，可以通过变分不等式方法将DTA 中的动态网络加载（DNL）过程表述为微分代数方程组（DAE）。设整个调度周期T按照调度 时 间 间 隔 ΔT分 为L个 等 长 时 段 ，T∈{T1，T2，…，TL}，其中TL为第L个等长时段，进而各个时段按照离散时长Δt分解为N个子时段t。这样，T时段中子时段t的DNL 过程可以用时间离散化后的DAE 描述为：

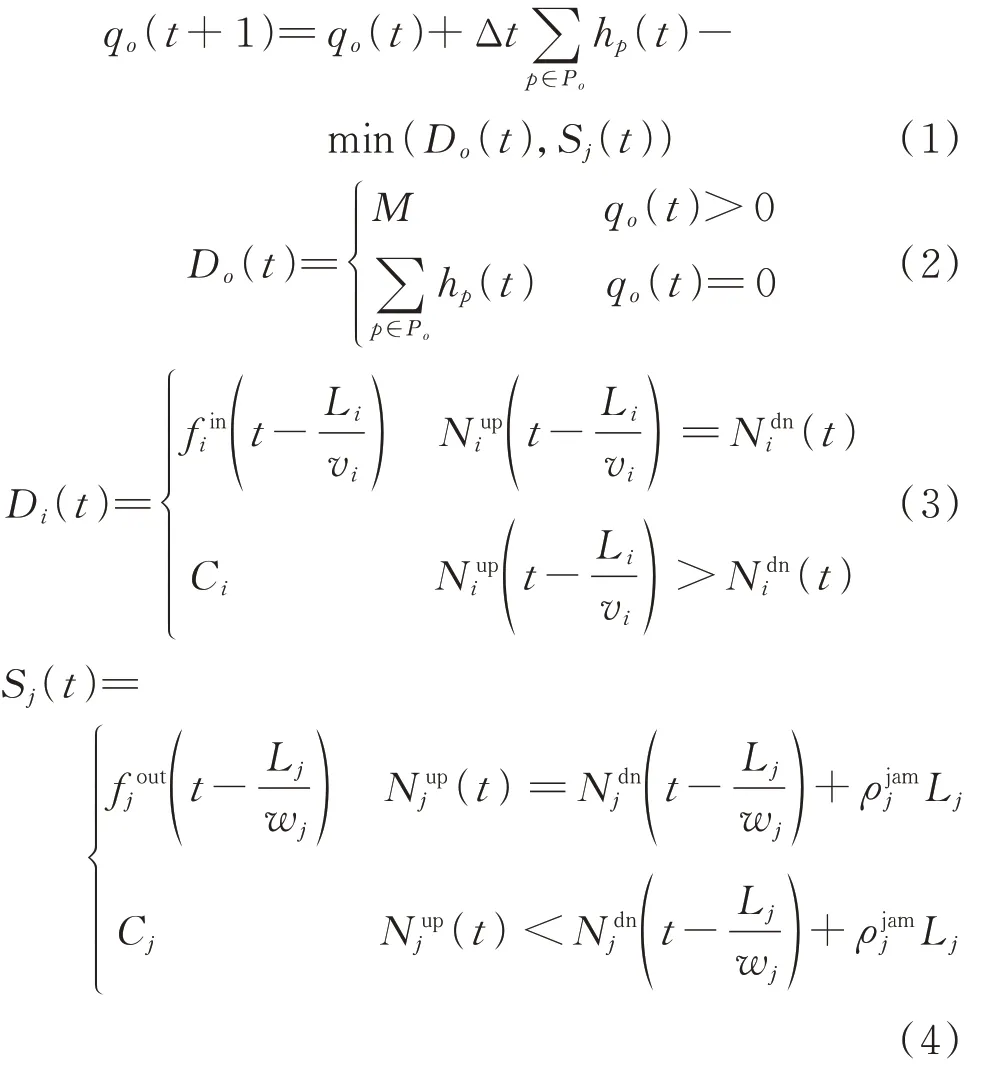
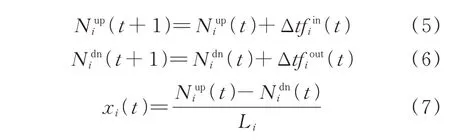
式中：qo(t)为t时段始发节点的点-队列长度；hp(t)为路径p的发车率；Po为始发节点为o的路径集合；Do(t)为离开队列的流量；Sj(t)为连接到始发节点o的路段j的供应车流量；M为大于路段j流量的充分大的正数；Di(t)为路段i的需求车流量；Nupi(t)和Ndni(t)分别为路段i的累计驶入车辆数和累计驶出车辆数；fini(t)和fouti(t)分别为路段i的驶入和驶出车流量；Ci为路段i的容量；Li为路段i的长度；vi和wj分别为正向波和逆向波的波速；ρjamj为路段j的拥堵密度；xi(t)为路段i的平均车流量。式（1）和式（2）构成了始发节点的动态点-队列模型；式（3）至式（7）描述了路段模型，假设通过交叉路口J的相邻路段i和j同时属于路径p。

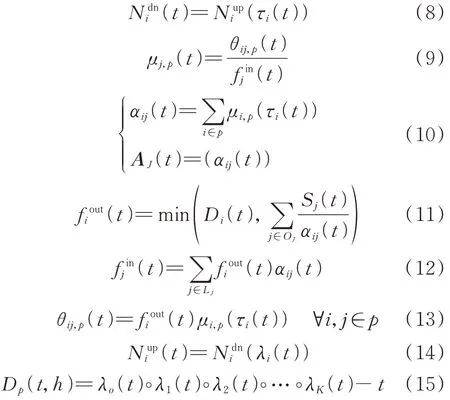
式中：τi(t)为t时段驶出路段i的对应驶入时间；μi，p(t)为路段i上属于路径p（即i∈p）的车流量百分比；θij，p(t)为同时通过属于路径p的相邻路段i和j的车流量；αij(t)为驶出路段i的流量中进入路段j的比例；AJ(t)为构成交叉路口J的流量分布矩阵；OJ为驶出交叉路口J的路段集合；LJ为驶入交叉路口J的路段集合；λi(t)为t时段驶入路段i的车辆的驶出时间；Dp(t，h)为t时刻在发车率h下的路径p驶出时间，p∈Pg，其中Pg为同时包含普通路段i和DWC路段ie的GV 路径集合；K为路径数；◦表示函数嵌套；λo(t)为驶出始发节点队列的时间。式（8）至式（13）为交叉路口模型，详细的DNL 过程见附录A。

基于DNL 模型式（1）至式（15），可以分别得到GV 和EV 的路径综合出行成本为：

式中：Ψg，p(·)和Ψe，p(·)分别为GV 和EV 的路径综合出行成本函数；γ为充电电价；Pe为仅包含ie的EV 路径集合；φ1，p(t，h)、φ2，p(t，h)和φ3，p(t，γ)分别为路径p提前/延后到达成本、行驶成本和充电成本，计算公式分别如式（18）至式（20）所示。

式中：Tij为车辆完成O-D 对(i，j)的目标时间；η为行驶时间成本系数；ξ为充电成本系数；γl和PEVl(t)分别为路径p上各个充电路段所接入的配电网节点l的充电电价和有功充电功率。

假设各个无线充电路段上行驶的混合车流中EV 车流的比例固定。单独的EV 不一定处于充电状态，但是众多EV 可作为一个整体充当配电网的充电负荷，从统计意义上可以粗略认为由配电网节点l提供的有功、无功充电功率PEVl(t)和QEVl(t)与由该节点供电的充电路段上的平均车流量线性相关，即

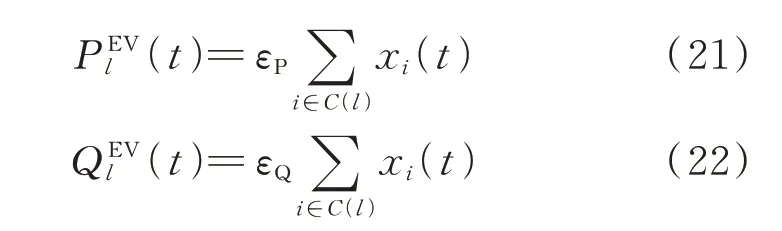
式中：C(l)为由配电网节点l供电的无线充电路段集合；εP和εQ分别为流量-有功功率和流量-无功功率转换系数。

不同于仅含GV 的交通网，同时含有GV 和EV的交通网将具有混合DUE 状态。参考文献［36］，将原有DUE 概念进行扩展，给出混合DUE 的定义：对于一个同时含有GV 和EV 的交通网，当且仅当满足式（23）和式（24）所示条件时，在路径发车率h*={(t)∈ΩT：p∈Pg∪Pe}下可达到混合DUE 状态，其中，ΩT为可行路径发车率集合。(t)＞0 ⇒

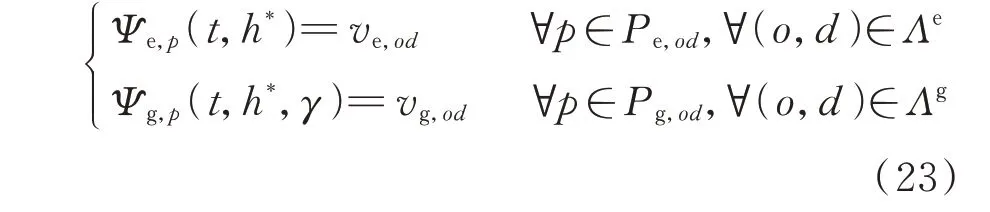
为了得到区域内的交通流分布，需要求解其混合DUE 状态，即满足式（23）和式（24），这等价于如下微分变分不等式问题［35］：

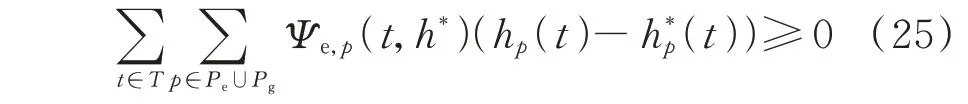
进而，利用微分变分不等式与不动点问题的等价性，可以建立求解h*∈ΩT的不动点算法。目前，对不动点算法的收敛性进行严格数学证明还存在较大困难，文献［37］仅就具有强单调递增算子的简单交通网情况给出了证明。由于该问题不属于本文的关注点，本文按照文献［33-35］的通常做法，通过大量数值仿真算例对收敛性进行了说明。交通网DUE 的不动点算法的求解详见附录A。

2.2 主动配电网的二阶锥松弛模型

2.2.1 主动配电网原始模型

本文以Distflow 支路潮流形式为基础，考虑一个包含节点集合Θ的配电网，支路ij∈ε连接节点i和节点j，其中ε为支路集合。由此得到T时段时主动配电网的原始模型为：

2.2.2 光伏发电模型

光伏发电的并网功率接口模型的有功出力和并网节点电压均为给定值，且无功出力满足：

2.2.3 ESS 模型

ESS 运行模型可表示为：

2.2.4 无功补偿装置模型

CB 装置运行模型可表示为：

SVC 装置运行模型可表示为：

2.2.5 二阶锥松弛模型

以最小化有功网损FPloss为目标函数，主动配电网的原始最优潮流模型为：

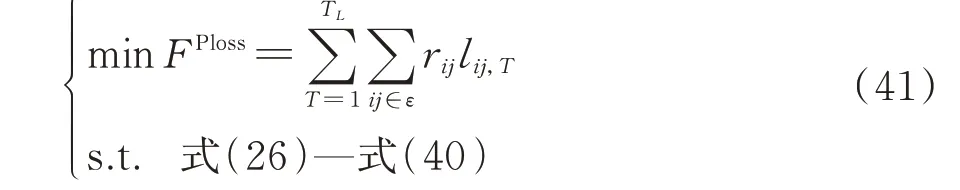
上述原始非线性模型难以求解，但可以采用二阶锥松弛技术将式（29）转化为以下二阶锥约束：

这样，可得主动配电网的混合整数二阶锥松弛模型为：

2.2.6 充电电价

充电电价应该反映节点新增单位负荷需求时的配电系统边际成本，包括主网购电成本、边际损耗成本以及配电阻塞成本。主网购电成本全网统一，本文假设其固定不变，作为基础充电电价。边际损耗成本反映各节点功率与系统网损间的关系，对于城市交通网所接入的配电网而言，地理范围较小，节点间边际损耗成本相差不大，故可忽略。阻塞成本反映系统各种网络约束及安全约束的影响。对于配电网而言，节点电压越限对系统安全运行的影响较支路功率越限更严重，因此本文基于节点电压越限指标形成节点拥塞电价。假设充电站j通过节点l接入配电网，则T时段的充电电价γl(T)为：

式中：γ(T)为基础电价；γ(T)β(T)为拥塞电价，其中β(T)为拥塞电价系数。当节点电压偏移很低时，拥塞电价也很小，充电电价仅包含基础电压；而随着节点电压偏移程度的增大，拥塞电价按指数增加并叠加在基础电价上，共同构成充电电价。需要注意的是，βcongl(T)在节点电压偏低和偏高时会改变符号，因此其调节作用与节点电压偏移方向有关。在节点电压偏低时，拥塞电价为正，可以缓解节点电压拥塞；而在节点电压偏高时，拥塞电价为负，会起到促进光伏消纳的作用。因此，实际应用中可以根据节点电压偏差的方向，取不同的电压调整强度参数。

采用式（44）定义的充电电价可以突出反映配电网安全运行状态对交通网车流量分布的影响和拥塞电价对缓解配电网安全运行压力的调控作用。

2.3 T-DN 联合运行模型

交通网和配电网通过无线充电站耦合在一起联合运行。一方面，交通网中充电路段的EV 车流量决定了配电网供电节点的充电负荷大小；另一方面，配电网供电节点的电压越限程度确定了相应的拥塞电价。

基于T-DN 联合运行模型可以协调利用交通网侧的车流量引导机制和主动配电网侧的各种有功/无功灵活性电源调度能力，有效消除交通网拥堵和配电网电压越限问题，并阻断T-DN 发生连锁性拥堵-拥塞。车流量引导机制通过调节不同DWC 路段上的电价，对EV 车流进行引导。在T-DN 联合优化中，交通网侧提供交通流的时空分布，进而转化为充电负荷的时空分布输入配电网侧，再将配电网侧得到的拥塞成本输入交通网侧，通过2 个系统的相互迭代逐步逼近优化运行点。详细的T-DN 联合优化算法见附录A。

3 算例分析

本章将建立电气化T-DN 联合运行的仿真算例，验证所提方法的有效性。其中，交通网和配电网采用修改的Nguyen-Baran＆Wu 33 节点系统，如图2所示。其中，WCS 表示动态无线充电站，PV 表示光伏电站。道路、线路和负荷的原始数据详见文献［38-39］，其他具体设置见附录B。

图2 修改的Nguyen-Baran＆Wu 33 节点系统Fig.2 Modified Nguyen-Baran＆Wu 33-bus system

3.1 拥堵-拥塞连锁性产生机理分析

在DWC 环境下，T-DN 耦合更加密切，EV 负荷的时空分布的变化更加剧烈。T-DN 联合运行模型为分析DWC 环境下EV 充电负荷对电网的冲击和配电网对交通网的反向影响提供了可能。本节展现了T-DN 中的拥堵-拥塞现象，并分析其连锁性产生机理。为此，须关注以下3 个场景中采用拥塞成本前后路网中拥堵状况的变化。图3 至图5 分别给出了3 个场景的相对交通流分布（relative traffic flow distribution，RTFD）热点图，其中红色表示路段高度拥堵。考虑到路段1 至路段10 的交通流基本不受拥塞调控机制的影响，各图中仅给出路段11 至路段19的RTFD。

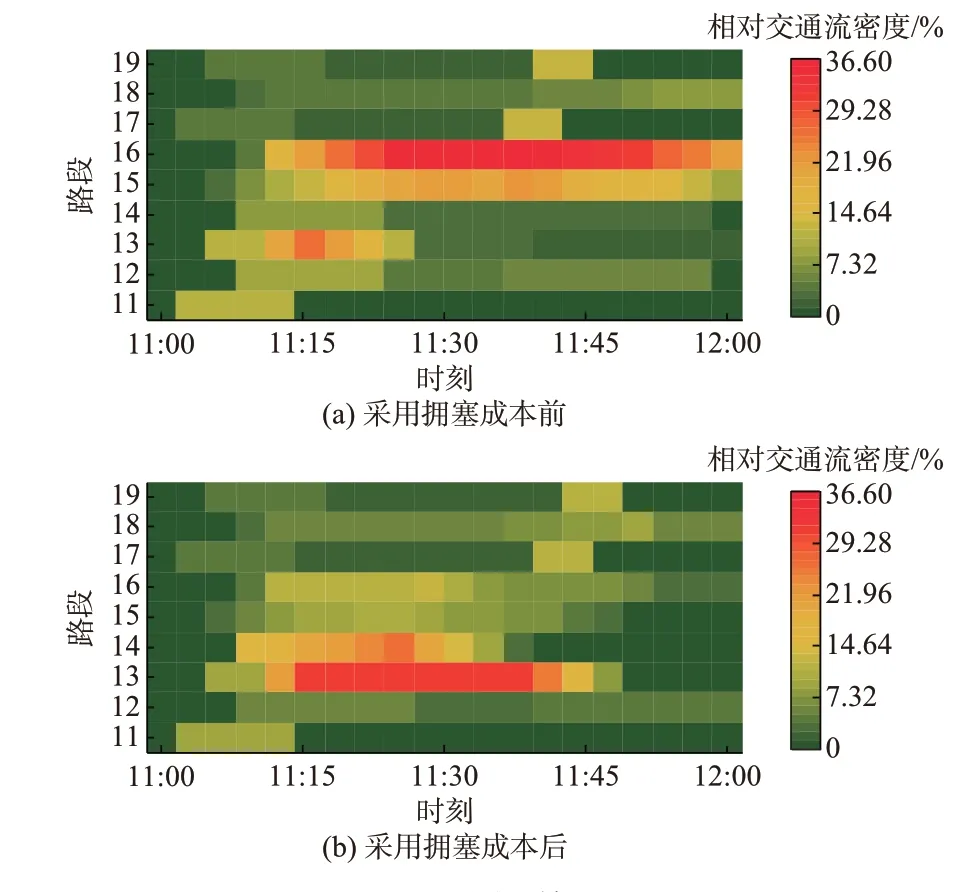
图5 场景3 的RTFDFig.5 RTFD of scenario 3

1）场景1：08：00—09：00，交通网出行高峰

该时段的特点是双网负荷整体较低，但个别路段的过大交通流会造成对应配电网节点拥塞。对比图3（a）和（b）可见，在采用拥塞成本前，路段16 存在交通拥堵，增大的交通流造成配电网节点14、15发生拥塞，节点电压幅值为0.94 p.u.，超越下限。而在采用拥塞成本后，路段16 的最大相对交通流密度由35%降低至23%，配电网节点14、15 的电压幅值提高至0.96 p.u.，处于允许电压偏移范围之内。同时，路段14 的最大相对交通流密度由7% 提高至11%。这表明在交通网高峰时段，EV 充电路段发生交通拥堵，进而导致配电网拥塞，但通过拥塞成本的调节可缓解交通网拥堵，并消除其造成的配电网拥塞。

2）场景2：12：00—13：00，配电网用电高峰

该时段的特点是配电网一般性负荷率较高，个别节点出现拥塞。此时段负荷率为0.92，且节点15有大量负荷。由图4（a）可见，在采用拥塞成本前，路段11 存在短时交通拥堵，同时配电网节点14、15处的一般用电负荷过大，导致电压超越下限（节点电压幅值为0.93 p.u.），处于拥塞状态。由图4（b）可见，采用拥塞成本后，与节点14、15 对应的路段16、11 的交通流都被大幅转移至路段14，导致路段14 的最大相对交通流密度由6%增至32%，发生严重拥堵。此时，配电网节点14 和15 的节点电压幅值分别提升至0.94 p.u.和0.93 p.u.，但电压仍超越下限。这表明，由配电网拥塞节点供电的电气化路段会将交通流转移至相邻平行路段，造成预期之外的继发性道路拥堵。

图4 场景2 的RTFDFig.4 RTFD of scenario 2

3）场景3：11：00—12：00，T-DN 双峰叠加

该时段的特点是路-电双网负荷水平均很高，交通高峰与一般用电负荷高峰重叠。此时段负荷率为0.9，且节点15 有大量负荷。由图5（a）可见，采用拥塞成本前，路段16 存在长时严重交通拥堵，导致配电网节点14 发生拥塞，节点电压幅值为0.91 p.u.，超越下限。由图5（b）可见，采用拥塞成本后，路段16 的最大相对交通流密度由35%降低至12%。同时，路段14 的最大相对交通流密度由8% 增至27%。配电网节点14 节点电压幅值均提升至0.93 p.u.，但电压超越下限问题没有改善。这表明，双峰叠加时采用拥塞成本已不能缓解路网的整体拥堵状况，虽然原始拥堵路段的交通流被疏导而使路况有所改善，但造成了其他路段新的继发性道路拥堵。

综合以上3 个场景，可得出以下结论。

1）拥塞成本建立了从配电网至路网的反向耦合

在不引入拥塞成本的情况下，交通网中的车流拥堵通过无线充电站，以充电负荷的方式影响配电网中的潮流分布，可能诱发配电网相应节点的拥塞。此时，路-电双网之间仅存在路网交通流向配电网电力流的单向耦合。引入拥塞成本后，配电网中的节点拥塞会通过拥塞成本影响EV 用户的综合出行成本，诱导EV 进行出行时间和行驶路径的选择，使交通网中的交通流产生再分配，交通流时空分布随之变化，从而改变交通网中的拥堵状况。此时，双网之间存在路网交通流与配电网电力流之间的双向耦合。

2）拥塞成本的双重调控作用

一方面，拥塞成本直接反映了配电网中节点电压越限情况，因此，采用拥塞成本可以缓解甚至消除配电网中节点电压越限问题；另一方面，拥塞成本所反映的节点电压情况是由该节点的一般用电负荷和对应路段的EV 充电负荷共同构成的总负荷所决定的。因此，拥塞成本间接反映了路网对应路段的EV 车流量状况。

在场景1 所代表的一般用电负荷水平较低而个别路段交通拥堵的情况下，拥塞成本可以起到疏导交通流的作用，即当交通网某些路段出现拥堵时，相应配电网节点拥塞引发的拥塞成本将引导EV 为降低充电成本而选择其他替代路径，从而起到缓解该路段拥堵的良性作用。引入拥塞成本并不会改变交通需求总量，因此拥塞成本作为反馈信号，通过配电网反馈调控路网的拥堵状态，使EV 车流重新分配，将重充电负荷转移至其他轻充电负荷节点，从而均摊配电网节点的充电压力。

而在场景2 所代表的配电网一般负荷高、个别节点出现拥塞的情况下，拥塞成本可能“虚假”反映对应路段的EV 车流量状况，从而诱发交通网一些路段出现新的拥堵现象。为了与采用拥塞成本前的路网中原有拥堵进行区别，称这种由配电网拥塞导致的借由无线充电站引发的路网拥堵为“拥塞成本继发性交通拥塞”，是一种T-DN 双向耦合情况下可能出现的不良后果。

3）拥塞成本的调控效果建立在双网调控资源充足的前提下

场景1 代表在单纯交通网调控资源不足的情况下，T-DN 可以借助拥塞成本反向耦合，调控交通流分布，缓解交通容量不足的薄弱路段的拥堵；场景2代表在配电网没有调控资源的情况下，拥塞成本的反向耦合作用会将有功/无功电源支撑能力不足的薄弱节点的拥塞问题转移至交通网，可能造成交通流紊乱，某些路段出现新的拥堵。

而在场景3 所代表的T-DN 双峰叠加情况下，采用拥塞成本对缓解交通拥堵的作用会大大降低，甚至出现连锁性拥堵-拥塞现象。其内在机理是当交通网发生拥堵时，大量的EV 车流会使得对应充电站的充电负荷大幅增加，进而与配电网中一般负荷高峰叠加，造成节点电压跌落，产生电力阻塞。但是由于配电网可以调用的有功/无功调节容量不足，配电网的拥堵只能反向传递至路网，强迫拥塞节点对应路段的车流分流至相邻平行路段。由于此时路网本身处于交通高峰，相邻平行路段的原有车流量也很大，拥塞成本的反向分流作用必然被大幅削弱，甚至可能造成路网拥塞的扩散，即原有拥堵路段没有得到缓解，同时相邻平行路段出现继发性新生拥堵。进而，路网的继发性新生拥堵会再次传递至配电网侧，可能造成配电网侧的继发性新生拥塞。这就是T-DN 在调控资源不足的情况下可能发生的大规模连锁性拥堵-拥塞现象，也解释了文献［20］中发现的用电高峰叠加出行高峰时可能出现大规模路网拥堵的问题。

另外，EV 渗透率对于节点电压偏移分布和电价调控效果均有显著影响，详细分析见附录C。

3.2 有功-无功协同优化效果分析

由3.1 节可知，产生连锁性拥堵-拥塞的本质原因是双网高峰时空重叠时，包括交通网路段容量和配电网有功/无功电源在内的双网资源不足或调度不合理。对于已经建成的T-DN，路段难以增容，但是可以通过协调优化调度主动配电网中包括分布式电源、储能装置和无功补偿装置等的多种有功/无功电源来消除配电网节点拥塞，阻断连锁性拥堵-拥塞的产生。

但是，配电网拥塞问题具有局部特性，即节点电压水平不是由全网有功/无功电源容量决定的，而是由发生拥塞的薄弱节点的当地或附近的有功/无功电源容量所决定。这样，在分析有功-无功协同优化效果时，需要区分有功/无功电源配置地点与配电网发生拥塞的薄弱节点一致时的容量匹配情况和不一致时的容量失配情况。详细仿真参数设置见附录D。

3.2.1 容量匹配情况

图6 至图8 给出了采用有功-无功协同优化前后的路-电双网运行状况，分为以下3 个方面。

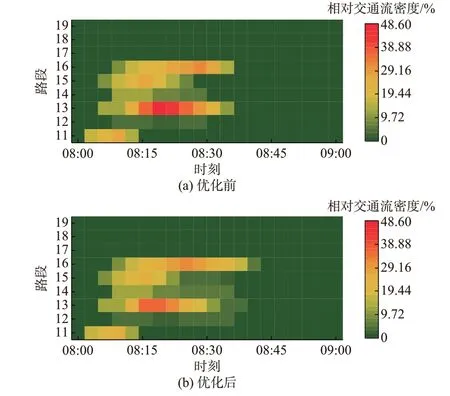
图6 优化前后的RTFD(08:00—09:00)Fig.6 RTFD with and without optimization(08:00—09:00)

图8 高光照率下光伏电站出力Fig.8 Output of photovoltaic power station with high illumination rate

1）交通流分布

图6 为08：00—09：00 时段采用有功-无功协同优化前后的RTFD。由图6 可知，拥堵路段13 的最大相对交通流密度由49%降低至37%，拥堵时间也大幅缩短，同时路段12 和15 的最大相对交通流密度分别由3.7%和27%提高至4.4%和降低至25%，均未达到拥堵水平。可见，整体路网拥堵状况有了显著缓解。

2）系统能耗

图7 给出了采用有功-无功协同优化前后的系统总能源损耗。由图7 可知，在08：00—12：00 时段，优化后系统总能耗大幅降低。特别是在08：00—09：00，总能耗降低最大，达到38%。可见，当路-电双网资源容量匹配时，协同优化效果理想。

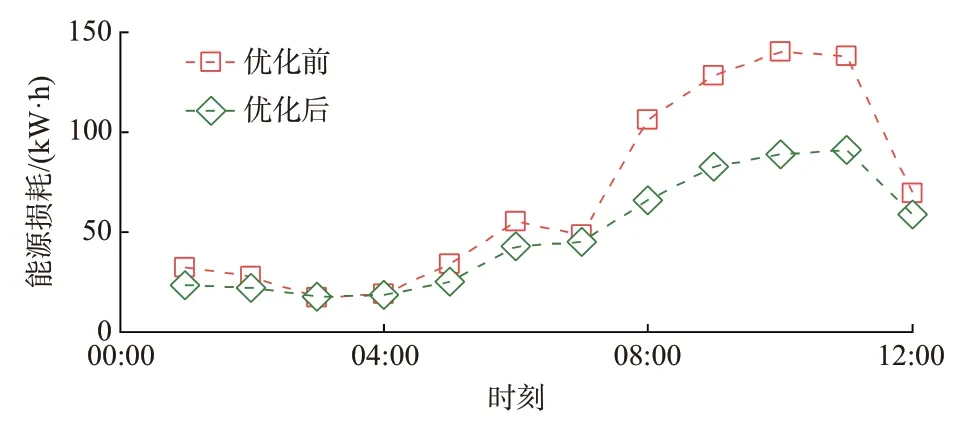
图7 优化前后总能耗对比Fig.7 Comparison of total energy consumption with and without optimization

3）光伏电站出力

由图8 可知，在高光照率、光伏电站高出力的情况下，优化后的光伏电站在07：00—08：00 和12：00—13：00 的消纳率分别由79%和74%提高至99%和90%。当光伏电站出力超过本地负荷需求时，由于电压约束的存在，为防止电压越限，光伏电站被迫大量弃光，表现为消纳率较低。本文采用EV 作为消纳光伏发电的手段，通过T-DN 的协同优化充分调用交通网侧和配电网侧资源，达到提高光伏电站出力消纳率的目的。详细的有功/无功电源调度策略见附录E。

综合以上3 个方面可知：优化之前，路段16 出现长时间的严重拥堵，该路段通过WCS6 接入配置光伏电站PV1 的节点14。同时，相邻平行路段11 通过WCS4 接入配置PV2 的节点29。而路段16 发生拥堵的时段里恰值光照率较高，使得PV1 和PV2 可以分别为节点14 和29 提供充足的有功-无功支撑。一方面，可以直接缓解配电网节点14 的拥塞程度；另一方面，也为相邻平行路段14 承载由路段16 转移过来的车流创造了条件。另外，在容量匹配的情况下，有功-无功协同优化有效地防止了车-网连锁拥堵-拥塞的产生，双网负荷均得到了均衡分配，总能耗得到明显降低。同时，由于光伏电站直接供给了高车流量路段的充电功率，出力有明显提高。这意味着在容量匹配的情况下，有功-无功协同优化可以有效解决光伏电站弃光问题，提高配电网对新能源的消纳能力。电价及不动点迭代曲线见附录F。

3.2.2 容量失配情况

采用有功-无功协同优化前后的RTFD 如图9所示，双网总能耗如图10 所示。为分析容量失配产生的影响，该算例使用的平行充电路段为路段11、14 和16。考虑到路段1 至10 的交通流基本不受拥塞调控机制的影响，仅给出路段11 至19 的RTFD。详细的有功-无功优化策略与优化前后PV 出力对比见附录G。

图9 容量失配时优化前后的RTFD(12:00—12:45)Fig.9 RTFD with and without optimization when capacity is mismatched (12:00—12:45)

图10 容量失配时优化前后双网总能耗对比Fig.10 Comparison of total energy consumption for dual-network with and without optimization when capacity is mismatched

由图9 和图10 可知，采用有功-无功协同优化前，交通网中路段11、14 和16 均未发生拥堵，配电网中也没有明显拥堵，但网损较高，达到75.81 kW·h。采用有功-无功协同优化后，配电网网损降低至70.35 kW·h，但路段11 的最大相对交通流密度由21%增大至35%，并且拥堵时间也有延长。这意味着由于交通路段与有功/无功电源容量失配，采用有功-无功协同优化后，协同优化在使得双网总损耗得到降低的同时，大幅增加了与大容量节点6 耦合的薄弱路段11（路段11 的拥堵密度远低于路段14 和16）的交通流，从而新生了不希望出现的继发性拥堵。

因此，当主动配电网中有功/无功电源的容量配置与交通网的薄弱路段不一致时，会严重削弱协同优化的效果。而为了实现容量匹配，需要在主动配电网的规划阶段根据交通网的交通流量预测结果，最优配置主动配电网中的各种有功/无功电源。但是固定地理位置的电源难以适应交通负荷空间分布的流动性，可能导致实际运行效果难以达到预期理想。

4 结语

本文基于DWC 模式搭建了T-DN 联合运行模型，分析了DWC 模式加深T-DN 耦合使得TDN 相互影响并在交通高峰和配电网用电高峰重叠时发生连锁性拥堵-拥塞现象的潜在机理，进而提出基于主动配电网的有功-无功协同优化方法以缓解该问题。

本文研究发现，在DWC 环境下，交通高峰和配电网用电高峰重叠使得EV 充电负荷对电网的冲击更大。同时，拥塞成本建立了从配电网至路网的反向耦合和路-电双网之间存在的交通流-电力流双向耦合。但EV 充电负荷与交通流分布直接相关，拥塞成本既直接反映了配电网中节点电压的越限情况，也间接反映了路网对应路段的EV 车流量状况，具有双重调控作用。在T-DN 联合运行的基础上，通过对交通网车流的引导以及调用主动配电网侧的有功/无功电源，可以有效克服T-DN 连锁性拥堵-拥塞问题，进而降低T-DN 系统总损耗。但是，协同优化的效果受到交通网路段容量和有功/无功电源容量配置空间匹配程度的影响。当有功/无功电源与配电网薄弱节点失配时，缓解交通网拥堵效果降低，甚至诱生继发性交通拥堵。

本文提出的方法本质上是一种源-荷-储时间协同调度，在实际应用中可能存在固定地理位置的电源难以适应交通用电负荷空间分布流动性的空间失配问题。下一步研究方向是考虑调用配电网的拓扑灵活性，即采用动态重构或软开关技术实现源-荷之间的空间动态匹配。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。