基于多目标优化的电力-交通系统协同运行分析

吕 思，卫志农，马骏超，陈 胜，彭 琰

（1. 河海大学能源与电气学院，江苏省南京市 211100；2. 国网浙江省电力有限公司电力科学研究院，浙江省杭州市 310014）

0 引言

加速推进能源供给侧的低碳化转型和能源消费侧的电能替代是助力中国实现“碳达峰、碳中和”目标的有效手段［1］。在此背景下，以电动汽车（electric vehicle，EV）为核心的电气化交通的广泛普及将显著加深城市交通系统和电力系统的耦合程度［2-3］。为了缓解EV 充电对电力系统的负面影响，促进充电负荷与新能源出力相匹配，同时提高用户在交通系统中的通行效率，有必要考虑由高渗透率EV 带来的两系统间的耦合特性，研究能源转型视角下的电力-交通系统协同运行［4］。

针对耦合系统的协同调度问题，文献［5］通过调整路段通行费和分布式电源（distributed generator，DG）出力来实现耦合系统的社会成本最小；文献［6］以制定充电站服务费的方式来引导EV 的充电选择，进而缓解交通阻塞并促进清洁能源消纳；文献［7-9］同时考虑路段通行费和充电服务费，通过对EV、燃油汽车（gasoline vehicle，GV）以及分布式电源的联合调控，实现耦合系统的 运行成本最小；文献［10］利用动态价格同时调控交通系统中EV 的时空分布和电力系统中灵活性负荷的用能情况，进而消除两系统的网络阻塞；文献［11-12］研究了耦合系统在节点边际电价作用下所达到的动态均衡状态。

上述研究均是以系统经济成本或全社会经济成本为目标。然而，在能源转型背景下，两系统产生的碳排放成为社会成本中不可忽视的重要组成部分。一方面，碳排放来源于交通系统中GV 的直接排放；另一方面，碳排放来源于EV 充电以及常规用电负荷在电网电源侧产生的间接排放。值得一提的是，EV 负荷与清洁能源出力的不匹配会造成电力系统碳排放量的增加，进而削弱交通电气化的减碳成效［13］。为此，文献［14］在目标函数中纳入了电力系统碳排放成本，通过优化EV 的行驶路径和充电地点来促进清洁能源消纳，实现两系统经济成本和电力系统碳排放成本的改善；文献［15］通过调控加氢站的服务费来引导氢燃料车的加氢选择，进而改善交通阻塞、电网经济成本和碳排放量，其中GV 的单位碳排放量被设定为与行驶距离相关的恒定常数；进一步，文献［16］采用宏观排放模型来刻画交通阻塞对GV 碳排放量的影响，提出差异化调控机制以实现耦合系统的低碳调度-经济调度。上述研究均以碳税的形式将碳排放量转化为经济成本统筹考虑。

然而，电力-交通耦合系统同时具有多主体特性和多目标需求。两系统的协同运行通常由系统主体（包括电力系统和交通系统）和用户主体（包括EV用户和GV 用户）共同参与。当前研究仅涉及多个主体的整体成本［5-10］，同时将碳排放量通过碳税转化为经济成本［14-16］，进而以单目标优化的形式来建模和求解。然而，单目标优化难以兼顾系统优化过程中多项性能指标或多个主体利益之间的协调，无法体现各目标之间的关系进而为两系统协同运行提供有效指导［17］。

为此，本文基于多目标优化来分析电力-交通耦合系统的协同运行。根据耦合系统中不同主体的利益以及不同的调度目标，将低碳调度-经济调度、电力系统最优调度-交通系统最优调度、系统最优调度-用户最优调度分别建模为3 组多目标优化问题，采用增强epsilon 约束法［18-19］获取帕累托前沿，并提出考虑公平性的折中解获取方法。最后，基于12 节点环形交通网和IEEE 33 节点配电网对各组多目标问题的调度结果进行了深入分析。

1 电力-交通系统多目标协同运行分析框架

电力-交通耦合系统中多主体、多目标及其相互间的耦合关系如图1 所示。其中，上层系统主体通过价格激励手段来调控用户的行驶/充电行为，以期达到理想的系统运行状态；下层用户主体基于价格信号和路网状况，以最小化各自的出行成本为目标来选择行驶路径和充电地点。

根据不同主体的利益以及调度目标的不同侧重点，可以得到以下3 组多目标优化问题：1）低碳调度-经济调度；2）电力系统最优调度-交通系统最优调度；3）系统最优调度-用户最优调度。其中，前两组多目标优化问题通常由系统主体内部进行考虑，其目的在于平衡电力系统和交通系统、经济成本和碳排放量之间的冲突性。基于各主体的理性假设，用户的出行成本通常不包括在系统主体的目标函数中［9］。第3 组多目标优化问题通常由独立于系统主体和用户主体的非盈利实体（如市场监管机构）考虑，其目的在于平衡两主体运行目标的冲突性，在降低系统运行成本的同时保障出行用户的利益，实现整体社会效益的提升。

2 电力-交通系统协同运行模型

2.1 基于混合用户均衡的交通分配模型

交通网是由若干节点和路段构成的连通图，可以表示为GT=(TA，TN)。其中，TN表示节点集合，包括起始点、到达点和十字路口节点；TA表示路段集合，包括连接各节点的交通路段。采用TR和TS分别指代起始点r和到达点s的集合，交通网中不同起始-终点（origin-destination，OD）对的出行用户从起始点r出发前往终点s，每个OD 对之间均由一组路径Krs连接。为了方便对EV 和GV 的充电/行驶行为进行统一描述，本文将常规交通路段扩展为3类路段，即常规路段TrgA、充电路段TchA（表征EV 的充电行为）和旁道路段TbyA（表征车辆路过充电站而不进行充电），该扩展方法已被广泛应用于电力-交通系统的协同分析中，详细模型可参考文献［5］。基于此，描述混合用户均衡的交通分配模型可叙述如下。

2.1.1 交通流量守恒约束

式（1）、式（2）描述了出行需求与路径流量的关系；式（3）、式（4）描述了路段流量与路径流量的关系。

2.1.2 行驶/充电时间

对于常规路段a∈，采用BPR 函数［20］来描述路段通行时间与车流量的关系：

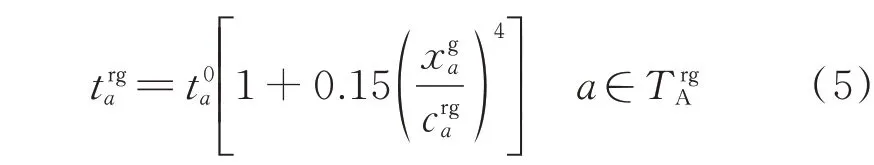
采用M/M/c/K模型来描述EV 在充电站的排队时间，则EV 在充电站a∈T中停留的总时长可以表示为［21］：

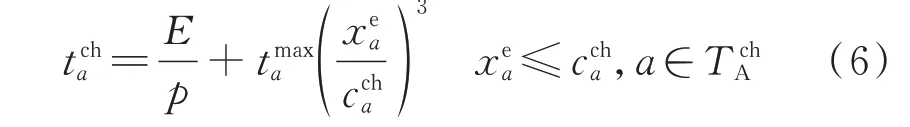
式中：E和p分别为单台EV 的充电需求和充电功率，进而E/p表示EV 的充电时长；为充电站满载时的排队时间；c为充电站能够同时服务的最大EV 数量。

2.1.3 出行成本

用户的整体出行成本是其所经路段的通行成本之和，主要包括时间成本、充电成本以及对系统运营商价格调控的响应成本。将GV 和EV 的出行成本

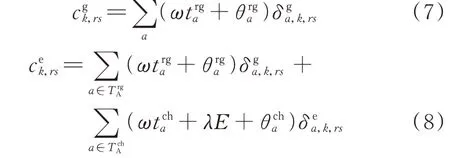
式中：ω和λ分别为出行用户的单位时间成本和充电站基准电价；和分别为系统运营商施加于交通路段和充电站的路段通行费用和充电服务费用。

2.1.4 混合用户均衡条件

假设出行用户在选择出行路径时，均以最小化自身的行驶成本为目标，那么交通流分布最终将达到一个稳定的用户均衡（user equilibrium，UE）状态，以至于所有用户均无法通过调整自身的路径选择来降低其出行成本［18］。该均衡状态的数学表述如下：

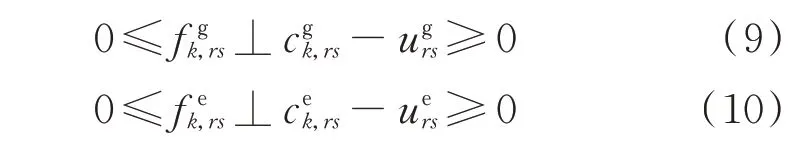
2.2 基于二阶锥松弛的电力系统支路潮流模型

本文采用二阶锥（second-order cone，SOC）形式的DistFlow 模型来描述电力系统中的潮流分布情况。其中，式（11）、式（12）表示节点功率守恒；式（13）定义了线路电压与电流的关系；式（14）表示二阶锥松弛；式（15）对节点电压、电流幅值的平方施加上下限约束；式（16）表示电源有功、无功出力的上下限。具体形式如下：

3 多目标优化调度建模及求解

3.1 多目标优化模型

首先，对交通系统和电力系统中的碳排放量和运行成本进行建模；然后，根据不同主体来定义相应的多目标优化问题。

3.1.1 碳排放量建模

本文采用以下宏观碳排放模型来描述路段通行时间与单位碳排放量的关系［22］：

电力系统中的碳排放主要由常规机组在发电过程中产生。本文假设常规机组的单位碳排放量与其发电量呈线性关系［14］，得到电力系统碳排放量ψemiPDN如下：

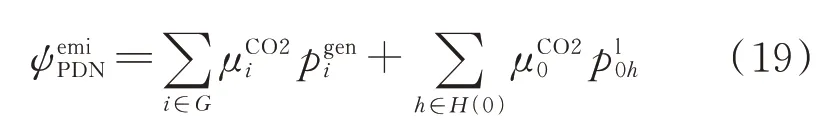
3.1.2 经济成本建模

交通系统的经济成本ψ主要由交通流的整体时间成本来体现，可以表示为：

电力系统的经济成本ψ主要包括发电成本和从主网购电的成本：

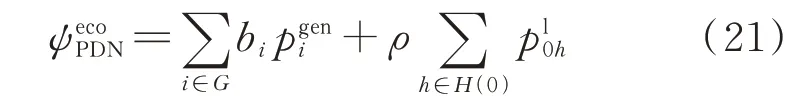
式中：bi为各机组的单位发电成本；ρ为主网购电费用。

3.1.3 多目标优化建模

结合上述碳排放量和经济成本的定义，可以建立以下3 组多目标函数组合：

1）M1（低碳调度-经济调度）：

2）M2（电力系统最优调度-交通系统最优调度）：

3）M3（系统最优调度-用户最优调度）：

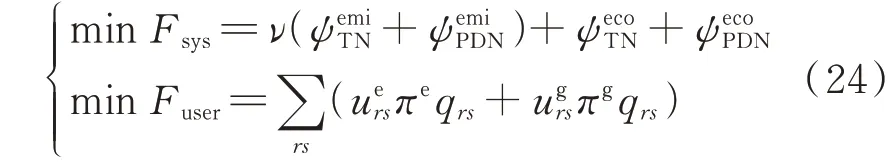
上述多目标优化问题的约束条件为：

式中：Femi和Feco分别为耦合系统的总碳排放量和总经济成本；FTN和FPDN分别为交通系统和电力系统的运行成本；Fsys为两系统的整体运行成本；Fuser为用户的整体出行成本；、和、分别为路段通行费和充电服务费的上、下限；ν为碳税。

鉴于低碳目标-经济目标的冲突性可以由M1建模和分析，本文在定义M2、M3 中各主体的目标函数时统一将碳排放量通过碳税转化为经济成本，将多主体各自的低碳调度-经济调度问题建模为单目标优化，以便于直观地分析不同主体之间的利益冲突。Fuser的详细推导过程如下：

3.2 增强epsilon 约束法

本文采用增强epsilon 约束法来求解上述多目标优化问题。其基本思想类似于传统epsilon 约束法，即选取主要目标函数进行单目标优化，同时引入epsilon 参数将其他目标函数（次要目标函数）放入约束条件中，通过逐步减小epsilon 值来获取原多目标优化问题的帕累托前沿。为了避免传统方法存在的弱有效解问题，增强epsilon 约束法通过引入松弛变量将与次要目标函数相关的不等式约束转化为等式约束，并将缩放后的松弛变量加入目标函数中，进而确保所得解的有效性［18］。以M1 为例，将其转化为式（27）所示单目标优化问题M。这里，将Femi作为主要目标并将Feco放入约束中，将次要目标函数Feco的取值区间等分为Neps段，使ε遍历每一个数值并求解相应的M，最终得到一组帕累托解集。显然，Neps越大，对帕累托前沿的拟合越准确，但是会显著增加计算时间，因此，通常基于对精度和效率的权衡来选取Neps。

3.3 模型线性化

为了提高每个单目标优化问题的求解效率，本文采用一系列线性化手段，将非线性模型转化为混合整数二阶锥模型。具体而言，对于较为复杂的高次非线性项ψ，首先引入辅助变量和，得到

进一步，对式（29）两边进行对数变换，同时引入极小正数υ来避免奇异，得到以下非线性约束：

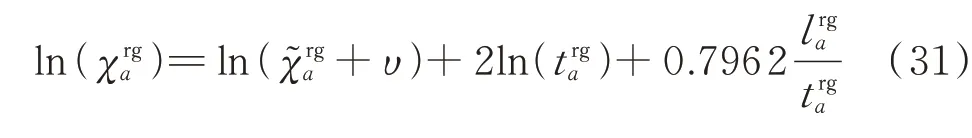
最后，采用分段线性化方法对模型中余下的常规非线性项（对数函数项、幂函数项、反比例函数项）进行线性近似。对于非线性互补约束（式（9）、式（10）），采用Big-M 法［23］将其转化为一组线性约束，此处不再赘述。

3.4 考虑公平性的折中解获取方法

本文以确保各目标公平性为原则从帕累托前沿中选取折中解，其基本思路如图2 所示。图中，fmax1、fmin1和fmax2、fmin2分别为各目标函数的最大、最小值；横轴和纵轴上的数值是各目标函数相对于理想点处目标函数值（即最小值）的倍数。在此基础上，通过计算并比较各候选运行点相对于理想点在不同目标方向上的增量（已归一化），将增量比接近于1 的运行点作为公平折中解。由于理想点是各自目标独立优化时所能达到的最优解，基于该原则获取的折中点能够确保各个目标（主体）所作出的妥协是接近的。

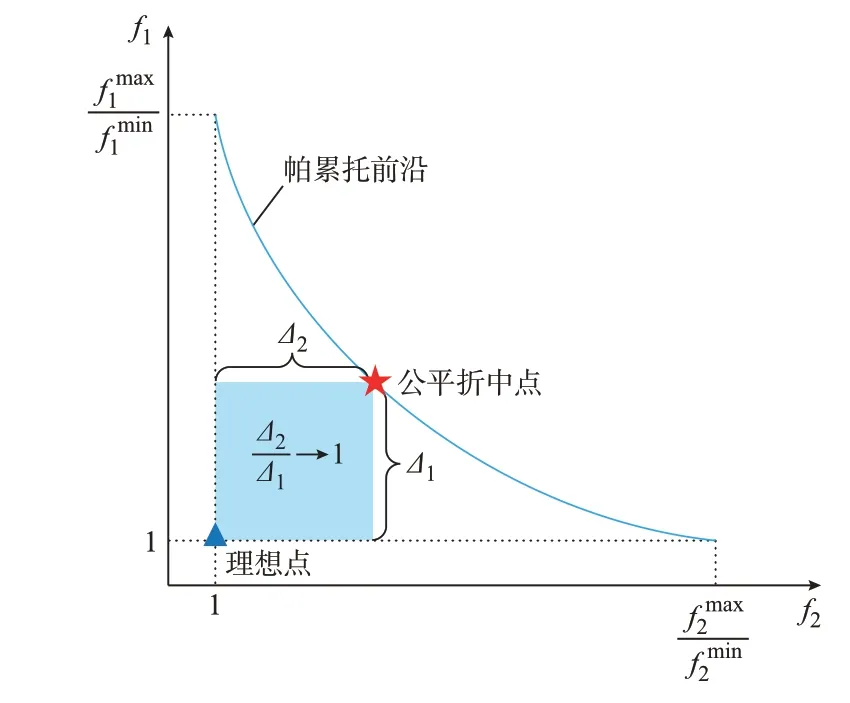
图2 考虑公平性的折中解Fig.2 Compromise solution considering fairness

对于包含3 个目标的多目标优化问题，公平折中点处应该确保两两目标（主体）之间皆公平，即3 组增量比均接近于1。因此，所选择的公平折中点应该满足：Δ2/Δ1+Δ3/Δ1+Δ3/Δ2→3，其中，Δ1、Δ2、Δ3分别为各组目标函数相对于理想点的增量，且上述增量比均取其假分数形式（即大于或等于1）。

4 算例分析

4.1 算例描述

为了确保电力-交通系统在空间上相匹配，本文效仿文献［24］，采用12 节点环形城域交通网［5］和两组IEEE 33 节点配电网［25］来构造电力-交通耦合系统，其网络拓扑结构和耦合关系如图3 所示，具体参数设置见附录A。本文所有仿真均基于GAMS 平台，通过调用Gurobi 求解器获取每个单目标优化问题的最优解。

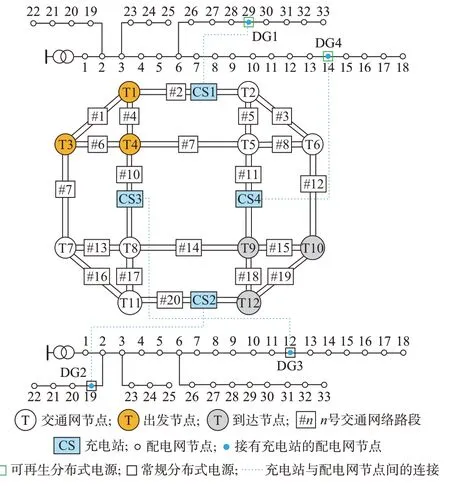
图3 电力-交通耦合系统Fig.3 Coupled power-transportation system

考虑到EV 充电负荷和可再生能源出力具有较强的随机性和波动性，本文根据二者不同的匹配程度构建以下3 个典型场景：

场景1（源荷匹配）：清洁能源满发（0.02 p.u.），单辆EV 充电需求为10 kW·h；

场景2（清洁能源过剩）：清洁能源满发（0.02 p.u.），单辆EV 充电需求为5 kW·h；

场景3（清洁能源不足）：清洁能源出力较低（0.005 p.u.），单辆EV 充电需求为10 kW·h。

4.2 多目标优化调度结果分析

4.2.1 低碳目标-经济目标

图4 所示为不同场景下低碳调度-经济调度的帕累托前沿。由于同一目标函数在不同场景下的数值存在较大差异，此处统一对其进行了归一化处理（下文同）。

图4 不同场景下的帕累托前沿及公平折中解（低碳调度-经济调度）Fig.4 Pareto frontier and fair compromise solution in different scenarios (emission dispatch-economic dispatch)

由图4 可知，不同场景下低碳目标-经济目标的冲突性有显著差异，该冲突性可以由总相对偏移量来刻画，即帕累托前沿两端相对于理想点的偏移量之和。本算例3 个场景中的总相对偏移量分别为16.3%、10.1%和17.9%。由此可见，清洁能源出力及其与EV 充电负荷的匹配程度是影响低碳目标-经济目标冲突性的关键因素。进一步，图5、图6 分别展示了不同调度目标下的EV 分布和分布式电源出力情况。此外，图5 还展示了在系统主体不进行价格干预时的EV 分布情况，其对应于各出行用户根据路网状况和充电站排队情况自行选择路径所达到的UE 状态。

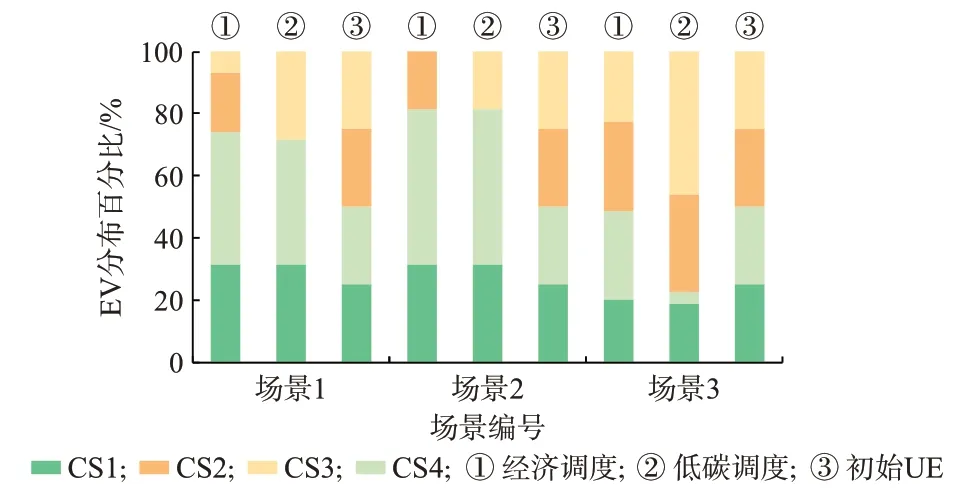
图5 不同场景下的EV 分布（低碳调度-经济调度）Fig.5 Distribution of EV in different scenarios(emission dispatch-economic dispatch)

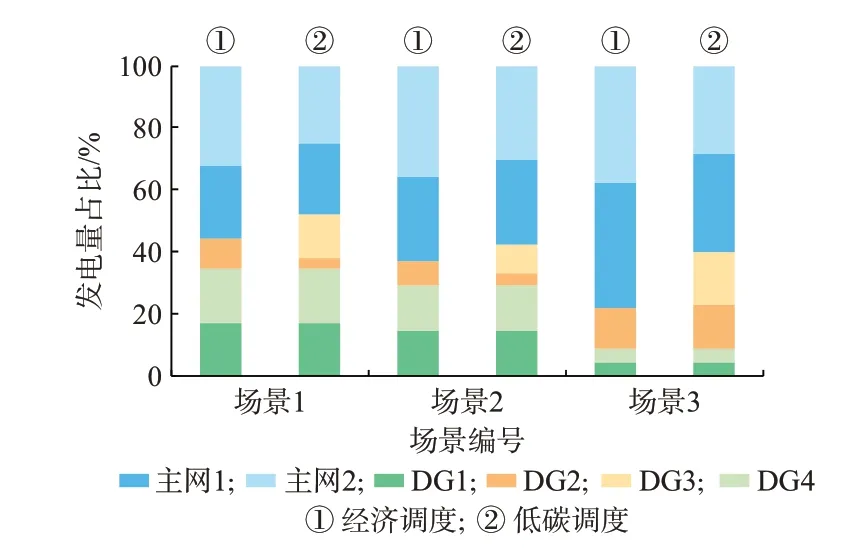
图6 不同场景下的分布式电源出力和主网购电占比（低碳调度-经济调度）Fig.6 Percentage of DG output and purchased power from main grid in different scenarios (emission dispatcheconomic dispatch)

可知，初始UE 状态难以满足两系统的经济运行和碳减排要求，因此，两系统均通过价格干预来调控EV 用户的充电选择。在充分利用清洁能源的基础上，充电站CS3（CS2）凭借相应机组较低的单位碳排放强度（单位发电成本）在低碳（经济）调度中接纳了更多的充电负荷。值得注意的是，场景2 中过剩的清洁能源未被充分利用，因为调度更多EV 前往充电站CS1 和CS4 充电会加重相应交通路段的阻塞程度和延长站内排队时长，进而造成更大的经济损失和更多的交通侧碳排放量。在场景3 的低碳调度中，分布式电源DG4 满发的清洁能源由常规用电负荷消纳，而相应EV 被调度至CS3 充电，进而避免像经济调度一样由主网直接向CS4 所在馈线的常规负荷供电，此举有效降低了碳排放量，也体现了EV 的空间灵活性对碳减排的作用。在折中解处，考虑到两目标的公平性，相应调度结果位于上述两种调度模式之间，且与低碳调度结果更为接近。

4.2.2 电网运行成本-交通网运行成本

在当前耦合关系下，各场景中两网的运行成本均同时达到了最优，两目标具有较强的一致性。为了探求影响两目标冲突性的因素，将CS1 和CS3 在电网中的连接位置互换，以分析清洁能源电站的地理位置对两网运行冲突性的影响。附录B 图B1 所示为新耦合场景下由两网运行成本构成的帕累托前沿，相应的EV 分布情况如图7 所示。

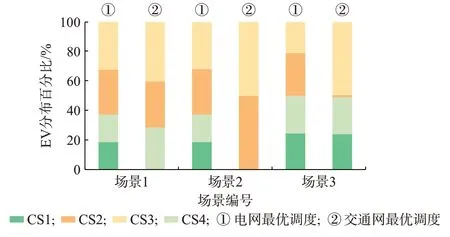
图7 不同场景下的EV 分布（交通系统最优调度与电力系统最优调度）Fig.7 Distribution of EV in different scenarios (optimal dispatch of transportation system and optimal dispatch of power system)

显然，新耦合场景下两目标具有显著的冲突，且与清洁能源出力及其和EV 负荷的匹配程度呈正相关。以场景2 为例，在初始UE 状态，大部分GV 会选择路段容量较大的外环行驶。因此，在仅考虑交通网运行成本时，会调度62.5%的EV 前往内环充电站充电，进而缓解外环交通网的阻塞情况，降低外环GV 因交通阻塞而产生的额外碳排放量和时间成本；在仅考虑电网运行成本时，会尽量调度EV 前往由清洁能源供电的充电站充电，而此举加剧了CS3和CS4 站内和相应路段的阻塞程度，增加了交通网的运行成本。由此可见，电网运行成本的改善主要源于EV 与清洁能源的最佳匹配，而交通网运行成本的改善主要源于对车辆行驶路径的引导，通过降低路段阻塞程度来减少GV 的碳排放量、提高通行效率。EV 最优行驶路径与最优充电地点的不匹配会造成两目标的冲突。当清洁能源充足时，由上述不匹配所造成的两网运行目标的冲突会显著加深（各场景下的总相对偏移量分别为7.5%、12.6%、3.5%）。

4.2.3 系统成本-用户成本

附录B 图B2 所示为由系统成本和用户成本构成的帕累托前沿。3 个场景中的总相对偏移量分别为1.8%、3.4%和1.1%，说明两目标之间的冲突随着清洁能源出力及其与EV 负荷匹配程度的增加而增强。进一步，图8、图9 分别展示了不同调度目标下的EV 分布和用户出行成本。

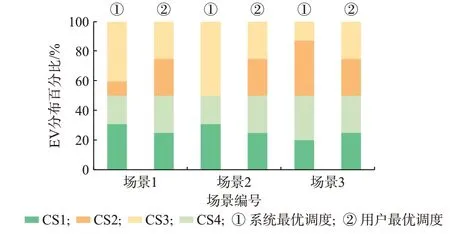
图8 不同场景下的EV 分布（系统最优调度与用户最优调度）Fig.8 Distribution of EV in different scenarios (optimal dispatch of system and optimal dispatch of users)

图9 各场景下不同OD 对的EV 用户出行成本（系统最优调度与用户最优调度）Fig.9 EV user travel costs from different OD pairs in each scenario (optimal dispatch of system and optimal dispatch of users)

可以发现，在考虑系统运行成本时，仅有50%左右的EV 被调度至清洁能源电站CS1 和CS4 充电，这也侧面证实了经济成本与碳排放量的冲突性。另一方面，系统运营商通过价格激励来调控用户的行驶/充电行为，使得各个OD 对间EV 用户的出行成本均高于用户最优调度状态的成本，其差值也与两目标的冲突性呈正相关。相比之下，GV 用户的个体目标与系统主体目标的冲突相对较小。为了确保系统运行成本最低，出行用户的总体成本在各场景中分别增加了近136、295、206 美元，但系统成本仅下降44、33、10 美元。显然，此举不利于促进用户积极响应系统运营商的价格调控，且有损整体社会效益和公平性。因此，3 个场景中的公平折中解均与用户最优调度的结果更为接近。

4.3 增强epsilon 约束法效果分析

本节以低碳调度-经济调度（模型M1）为例来说明增强epsilon 约束法相较于传统epsilon 约束法［26］的优越性。附录B 图B3 所示为场景1 中采用不同方法得到的帕累托解集。可以发现，传统epsilon 约束法得到的解集中包含了一组受支配解（弱有效解），相比于非支配解，其在相似经济成本下的碳排放量更高，因此不属于帕累托前沿，该结果也验证了增强epsilon 约束法在获取有效解上的优势。进一步，附录B 图B4 展示了不同Neps取值下增强epsilon约束法所获取的帕累托解的数量和分布，其相应的计算时间分别为16、25、33、39 min。显然，帕累托解的数量和求解时间均与次要目标函数的分段数成正比，更细致的分段有利于更准确地拟合帕累托前沿的形态，进而便于决策者根据不同工况做出非劣决策。

5 结语

本文综合考虑电力-交通耦合系统的多主体特性和多目标调度需求，提出了电力-交通系统多目标优化调度模型。算例测试结果验证了低碳与经济、系统主体与用户主体、电力系统与交通系统之间调度目标的冲突性。其中，低碳目标与经济目标的冲突主要源于电力系统中发电机组经济参数与碳排放量的不匹配，以及由低碳机组供电的充电站位置与交通系统路段容量的不匹配，后者同样引发了电力系统与交通系统运行目标的冲突；系统成本与用户成本的冲突主要源于个体目标（个体经济性最优）与整体目标（整体经济和碳排放最优）的不一致。上述不匹配所造成的各组目标的冲突程度均与清洁能源出力与EV 负荷的匹配程度相关。基于公平性的折中解获取机制能够有效缓解各目标的冲突。此外，上述冲突也强调了从规划层面（路段容量、充电站位置、清洁能源匹配等）来缓解各主体之间运行目标冲突的必要性。

后续工作将以本文模型和框架为基础，进一步考虑交通流的动态特性、用户行为和分布式电源出力的随机性，以及EV 电池容量对充电需求的影响等，以增强模型的实用性和结论的可靠性。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。