船模拖曳水池大体积混凝土跳仓施工温度场模拟
2022-07-04张志敏徐大为
张志敏 徐大为
上海建工五建集团有限公司 上海 200063
在工业与民用建筑结构中,一般现浇的连续墙结构、地下构筑物及设备基础等是易因温度收缩应力引起裂缝的结构,通常称为大体积混凝土结构[1]。以往大体积混凝土施工采用的后浇带法,普遍存在施工麻烦、施工缝多、易漏水等缺陷,因此目前许多工程选择采用跳仓法施工大体积混凝土。跳仓法依据“抗放兼施,先放后抗”的理论对大体积混凝土进行分块,先跳仓浇筑第一阶段的仓块,给予时间让其释放应力,后期浇筑剩余仓块,利用混凝土性能抵抗较小的温度收缩应力。
为保证跳仓施工方案的合理性和工程的质量与安全,实施跳仓前通过有限元软件对大体积混凝土进行建模分析,能有效模拟混凝土浇筑过程以及跳仓结果温度场。
1 工程概况
某高校多功能船模拖曳水池长度约300 m,宽度16 m。水池深7.5 m,池壁高度8.3 m,池壁根部厚度为1 m,顶部厚度为0.6 m;底板厚度0.8 m,池壁下方加厚至1 m(图1)。水池混凝土施工采用跳仓法,分仓时第1块为31 m,其余每隔26 m设置分仓,中间设置施工缝。施工时安排四个施工班组分别对墙板和底板进行隔块跳仓施工,底板施工与墙板的施工间隔10 d。
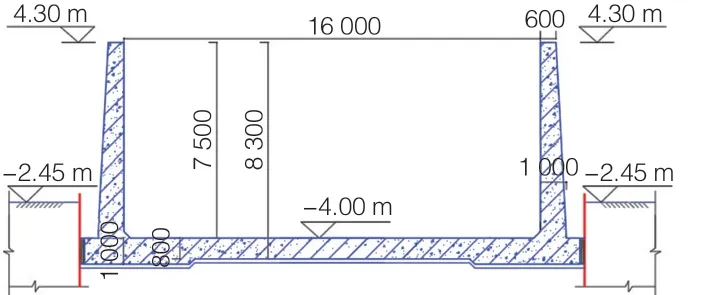
图1 水池设计截面示意
水池底板及池壁混凝土强度等级为C30,抗渗等级为P6,水泥选用P·O 42.5水泥,具体混凝土配合比如表1所示,混凝土坍落度为120 mm±30 mm,砂率为43%。

表1 混凝土配合比设计
2 温度场仿真计算
2.1 计算模型
为简化模型网格划分时的程序和划分后的单元形状,在建模时对水池截面做了简化处理,具体表现在水池底板厚度统一为1 m,水池壁上下厚度统一为1 m。建模时选取水池周围5 m内的土体加入计算,表现混凝土浇筑时与下方土体热量传递过程。
有限元模型采用热单元SOLID70,该单元是一个具有导热能力的单元,共有8个节点,每个节点只有1个温度自由度,该单元可用于三维的稳态和瞬态热分析问题[2]。经过网格划分后有限元模型如图2所示。

图2 水池有限元模型
2.2 参数分析
2.2.1 水化热
水化主要是水泥的化学反应生成凝胶体(托钵莫来石)的过程,即混凝土硬化过程[3]。在这反应过程中放出的大量热量即水泥的水化热,其数值与龄期的关系式在工程上一般有指数式、双曲线式和双指数式三种。经过工程实际应用和研究发现双指数式在曲线拟合方面更加符合实际水化放热过程,因此本文选用朱伯芳院士的双指数式[4],其公式为:

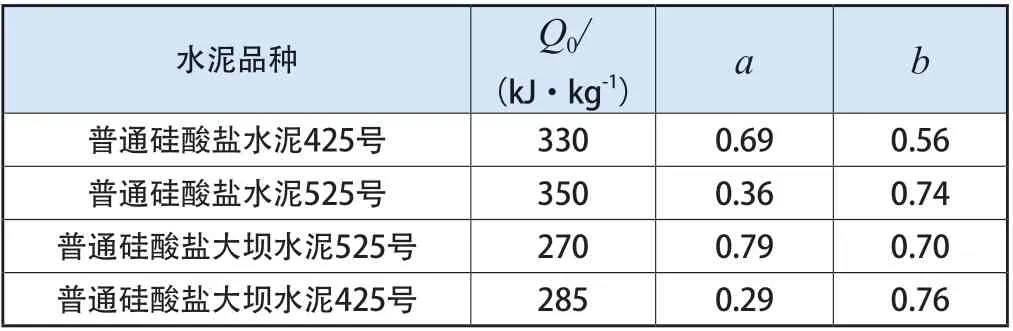
表2 水泥水化热常数
不能将水化热公式直接施加于模型,应当将其转变为生热率HGEN,即单位时间内混凝土的生热量。将水化热对时间进行求导得到生热率式(2)为:

上式为水泥生热率,在实际工程中混凝土的胶凝材料不但有水泥,还掺有粉煤灰等,这些粉煤灰也会产生一定量的水化热,所以在计算水化热时,还应将粉煤灰产生的水化热折算为水泥,将其产生的水化热也计算在内[5]。由上可得混凝土生热率为:
鉴于双硫酯类化合物在聚合物合成中的重要性,本文设计合成了两例新型的含羧基官能团双硫酯类化合物,并通过双硫酯化合物结构上的羧基与纳米二氧化硅表面的氨基之间的酰胺化反应,成功的合成了两种含双硫酯结构的纳米二氧化硅。

值得注意的是,时间τ的单位为d,在进行数值模拟时应当根据定义的时间步长进行换算,本文设定计算时间步长全程为1 h,根据上式及参数取值计算混凝土生热率为:
HGEN=(0.69×0.56×330/24)×(t/24)0.44×exp[-0.69(t/24)0.56]×(190+0.25×70)。
2.2.2 材料参数
在数值模拟过程中一共定义了混凝土和土体这2种材料,2种材料的参数最好根据具体工程条件实际测量得到,本文中2种材料参数具体见表3。

表3 材料基本热力学参数
2.2.3 初始条件和边界条件
为求得确定的热传导方程的解,需要定义初始条件和边界条件,此处表现为材料的初始温度和不同材料之间的热量传递条件。材料的初始温度在上文已有定义。边界条件中的一种为空气和混凝土的热对流,属于热传导方程的第三类边界条件,其边界条件可以作为面荷载施加于实体的外表面计算固体与流体的热交换[6]。此种边界条件需要对环境温度进行定义。另一种为土体与混凝土接触的第四类边界条件,此边界条件不需要再额外定义。
为模拟环境温度变化,文中采用的余弦函数变化表达式为:

2.3 施工过程模拟
为实际反应跳仓浇筑过程,应当根据施工方案将有限元模型进行分仓,采用“生死单元”技术实现顺序浇筑的工况。所谓“生死单元”即将模型的刚度(或其他分析特性)矩阵乘以一个极小的因子,使其暂时失效,并按照施工顺序将其逐个激活。本工程模拟时将有限元模型共分为11个仓块,分底板Ⅰ→底板Ⅱ、墙板Ⅰ→墙板Ⅱ三步进行激活(图3)。

图3 水池分仓示意
3 温度场结果分析
混凝土水化反应相关试验和研究表明,混凝土水化放热反应初期,水化反应特别剧烈,此时由于混凝土内外导热和对流条件的差异,热量传递速度差距很大。内部热量无法快速散发,内部温度急剧上升;表面与空气对流导致热量散发较快,冷却也较为迅速,此时混凝土内外温度梯度达到峰值。本工程含有底板和墙板2种混凝土结构,为研究不同结构、不同位置温度随时间的变化,在时间后处理系统中分别提取了各个位置的时间温度数据进行分析。
3.1 底板温度场分析
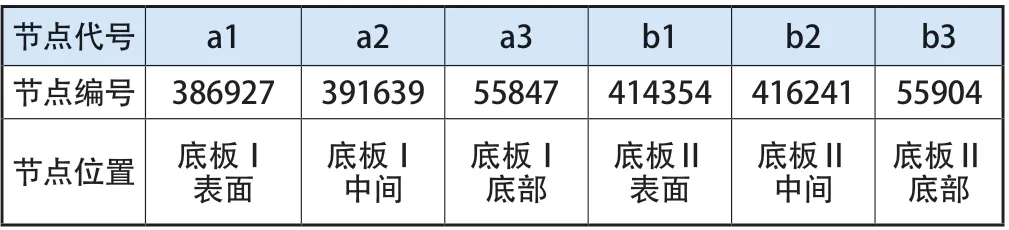
表4 选取的底板节点
针对以上节点,通过时间后处理系统可得相应的节点温度-时间数据,导出数据并绘制曲线,如图4、图5所示。

图4 底板Ⅰ节点温度-时间曲线
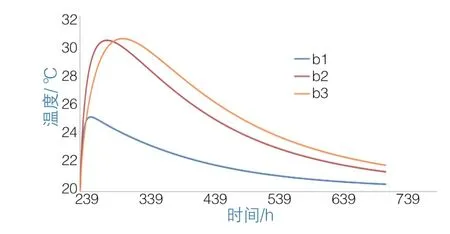
图5 底板Ⅱ节点温度-时间曲线
由温度-时间关系曲线上看,2次浇筑的底板放热与升温进程基本一致。表面由于存在与空气的对流条件,温度增幅最小,温度峰值为25 ℃,仅升高5 ℃左右,其温度峰值也出现得很快,在24 h前后便已达到峰值,随后持续降温至环境温度。中间与底部的温度峰值基本一致,为30 ℃,相比浇筑温度上升了10 ℃左右。不同的是底部出现峰值的时间在72 h前后,而中间部分出现峰值的时间在50 h前后。从曲线形状来看无论是升温过程还是降温过程,底部都相比中间部分更为平缓。出现以上现象主要有2个方面的原因:一是本工程的混凝土厚度不大,混凝土内部热量传递不会特别困难,不会出现中间热量持续累积的情况;二是在此模型中未加入保温措施,表面混凝土直接与空气接触,热量散发较快,底部与土体接触热量散发较慢。
根据温度-时间曲线,在混凝土底部和中间到达峰值时,混凝土表面正处于迅速降温阶段,此时内外温度梯度最大,由此产生的温度应力也最大,混凝土的开裂往往在此时发生。根据温度-时间曲线变化,分别在72、240、312 h和720 h时截取底板中间截面的温度分布和温度梯度分布(图6、图7)。

图6 底板中心截面温度场分布
由图6、图7可看出,在第1次底板浇筑完成后的72 h左右,内部温度到达峰值,底板温度整体呈现内部高两侧低的趋势,此时内外温差在9.0 ℃左右。在浇筑完成后240 h时,第1次浇筑的底板基本冷却完成,内外温度梯度为3.5 ℃左右。到浇筑完成后312 h时,第2次底板浇筑和第1次墙板浇筑的水化放热最剧烈,第2次浇筑的底板温度达到峰值,为33.0 ℃。与第1次底板浇筑72 h时温度分布不同的是,此次底板混凝土与墙板交界处在底板水化热和墙板水化热的双重影响下温度达到峰值,底板Ⅱ温度分布也与底板Ⅰ温度分布略有不同。此时内外温度梯度也达到峰值,为13.0 ℃。浇筑完成后720 h,所有混凝土冷却基本完成,内外温度梯度在2.0 ℃左右,整体温度在此时比较均匀。

图7 底板中心截面温度梯度分布
3.2 墙板温度场分析
对墙板拟计划选取代表性仓块的内外表面和中间的中心节点作为分析对象,但由于墙板两侧表面的对流条件和基础条件完全一致,因此墙板两侧表面仅选择代表性仓块的外侧表面中心节点作为分析对象(表5)。针对墙板节点通过时间后处理系统可得到相应的节点温度-时间数据,将数据导出并绘制曲线图,如图8、图9所示。
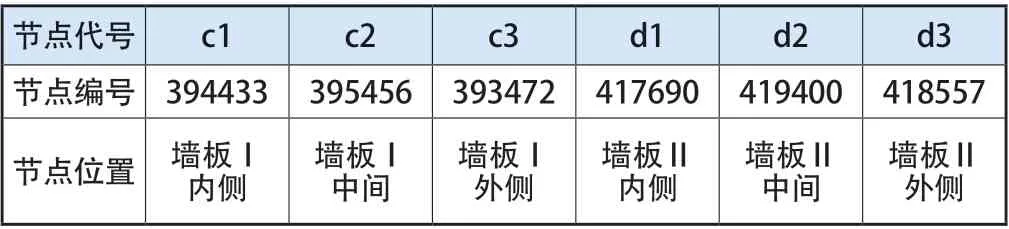
表5 选取的墙板节点

图8 墙板Ⅰ节点温度-时间曲线

图9 墙板Ⅱ节点温度-时间曲线
通过墙板与底板温度-时间曲线对比可看出,墙板内外总体温度-时间曲线规律与底板一致。底板和墙板的温度解析曲线主要差别在于二者的升温速率和降温速率的差距。通过对最高温度所对应的时间点分析可发现,墙板Ⅰ和墙板Ⅱ在浇筑后的温度迅速上升并在浇筑完成后20 h左右达到最高温度,随后温度迅速降低。造成此种结果的根本原因为墙板两边都存在与空气的对流条件,热量散发很快,导致内外温度降低速度相对于底板更迅速。
由图9可看出,在浇筑完成后20 h左右时,墙板Ⅱ最高温度达到33 ℃左右,经过对浇筑过程热量传递分析认为,由于先前浇筑的墙板Ⅰ和底板Ⅱ的水化热影响,导致墙板Ⅱ浇筑时温度会出现新的峰值,但此温度峰值也会随时间进程迅速降低。
根据以上墙板温度-时间曲线,截取了x=1处的y、z截面(此截面包含墙板的中间截面和其下的底板截面)在浇筑完成后260、480、500、720 h的温度云图和温度梯度云图(图10、图11)。分析此截面求解结果是为了分析墙板温度变化过程和在z方向(垂直方向)上的温度梯度情况。

图10 垂直方向截面温度云图
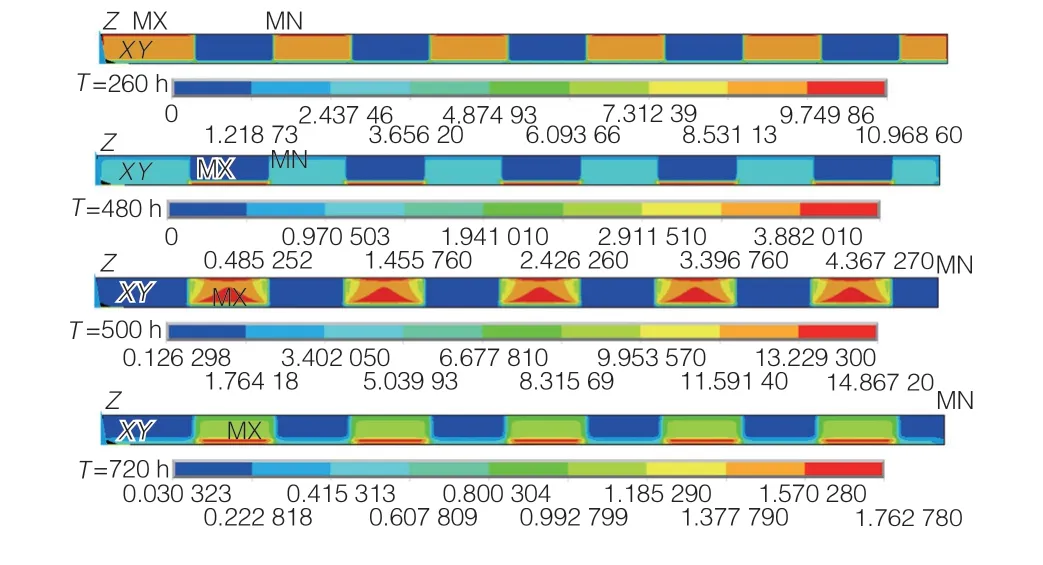
图11 垂直方向截面温度梯度云图
从图10、图11可看出,墙板总体呈现中间向四周降温的趋势,且在浇筑完成后的240 h内部温度几乎降至环境温度。从温度梯度云图来看,大温度梯度主要为底板和墙壁的温度梯度差,在墙板Ⅱ浇筑完成后的20 h发现,底板和墙板的垂直温度梯度达到14 ℃,为整个模拟过程的最大温度梯度。受这个温度梯度影响,在这个时间段垂直方向上的温度应力会有一个明显的增大,容易产生混凝土裂缝。
3.3 交界处温度-时间曲线分析
跳仓法施工模拟中由于先后浇筑顺序的影响,后浇混凝土浇筑时先浇混凝土已经冷却过1个施工间隔,温度比较均匀,当后浇混凝土大量发热时两者存在一个较大的温度差。基于这个温差,后浇混凝土散发的温度部分向先浇仓块传递,导致先浇仓块温度再次上升。通常这个温度的升高仅发生在2次浇筑混凝土交界处边缘,无法影响到仓块中心温度。在本工程中包含了墙板与墙板、墙板与底板和底板与底板3种交界条件。由于墙板与底板的交界处截面温度云图已经在图10和图11中充分体现,因此此处选取了底板与底板交界处的表面、中间和底部节点,墙板与墙板交界处的表面、中间节点作为对象(表6),并绘制其温度-时间曲线进行分析(图12、图13)。

表6 选取的交界处节点

图12 底板交界处节点温度-时间曲线

图13 墙板交界处节点温度-时间曲线
从墙板与墙板、底板与底板交界处节点温度-时间曲线来看,在后续浇筑过程中升温最大的点为底板Ⅰ的底部节点,内外最高温处与表面温差均在3 ℃左右。相比上述的底板内外温差和墙板内外温差要小很多,由此可看出后浇部分对先浇部分存在温度影响,但这个影响主要存在于二者交界处的区域,且对内外温差影响不会太大。
4 结语
本文通过对船模拖曳水池工程跳仓浇筑方案的有限元模拟分析,得到了在浇筑过程中的各个部位随浇筑进度和时间进程的温度变化情况。根据该项目跳仓施工方案模拟结果来看,整个工程混凝土最大温度控制在35 ℃以内,最大温度梯度在15 ℃以内,处于较为安全的温度状态。
该结果的最大温度主要出现在底板混凝土内部、墙板Ⅱ内部和墙板Ⅱ与底板Ⅱ交界处。最大温度梯度出现在第2次底板浇筑时的内外温度梯度和第2次墙板浇筑时的垂直温度梯度。对以上温度梯度较大的部位,在实际施工过程中应当预先做好一定的散热措施,以减小温度梯度。
墙板浇筑时,在浇筑模拟过程中未设置保温条件,且存在两边与空气的对流情况,导致升温降温过程十分迅速,实际施工过程中应对墙板两侧重点实施保温措施。
数值模拟结果无法完全还原实际工况,只能作为理想条件下对施工方案的结果模拟。模拟结果可作为参考条件来计算浇筑过程中各个部位的保温、散热需求,根据该需求可在浇筑前提前做好保温、散热的工程准备。
