一种动态校正的信号双尺度近邻定位方法
2022-07-04孙顺远朱红洲秦宁宁
孙顺远,朱红洲,秦宁宁,2
(1.江南大学 轻工过程先进控制教育部重点实验室,江苏 无锡 214122;2.南京航空航天大学 电磁频谱空间认知动态系统工信部重点实验室,江苏 南京 211106)
目前,室内定位技术大多基于WiFi[1]、蓝牙[2]射频识别等技术,但无线信号由于多径效应、电磁干扰等原因易产生波动[3],且随着定位区域的增大,计算复杂度也随之增加。因此,如何降低信号波动,减小计算复杂度,提高定位精度,成为主要的研究方向。蓝牙信标仅用于广播信号强度,不能提供到达时间差[4]以及到达角度差[5]等信息,故选择基于接收信号强度(RSS)的指纹匹配方法最为合适,建立参考点接收信号强度和坐标之间的匹配关系以实现室内定位。
为减小信号接入点(Access Point,AP)的信号波动,采用数据滤波进行解决,增加参考点处接收信号强度的采集频次,引入滤波器处理接收信号强度数据以减小定位误差[6]。文献[7]中对离线指纹数据分区建模,构建多个子区域模型,有效地降低了计算复杂度。但基于接收信号强度信号的室内定位易受到墙体干扰以及多径效应影响,导致不同参考点处的接收信号强度相同,造成分区的错误,故需结合区域物理坐标构建分区模型。文献[8]中提出建立数据校正的方法,通过高斯过程回归(GPR)模型训练信号距离模型,设定阈值判断是否需要校正,减小接入点信号波动的影响。文献[9]中提出核函数强化学习的方法规避未知干扰源的干扰,可以用于有效的规避环境中的干扰因素,减小定位误差。文献[10]中讨论了不同近邻k值下的定位精度效果,随着k值的增大,定位精度变高,到达某个值后,呈下降趋势,但实际每次最优k值不是固定的。针对这一问题改进,文献[11]中提出动态加权近邻算法,通过相似度的均值作为动态k值求取的阈值,以提升定位精度。文献[12]中以区块链的技术共享信号节点,有效地减小算法的计算复杂度。
在复杂的大型目标区域中,上述定位方法计算复杂度较高;随着接入点信号波动引起接收信号强度数据异常点的增多,定位精度较差。针对这些问题,提出一种动态高斯校正的双尺度近邻定位方法(Two-Scale Nearest Neighbor positioning algorithm under Dynamically Gaussian Correction,DGC-TSNN),根据物理连通性划分区域,采用一对多支持向量机(OVRSVM)训练分区模型,精确信号变化区域。以高斯过程回归训练接入点信号距离模型预测分区路径损耗特性,校正信号波动值;引入信号相似度和信号差异值,构建信号双尺度近邻定位算法;引入环境参数进行动态获取近邻k值,减小算法定位误差。在环形走廊和房间区域中布置蓝牙信标,测试分析提出算法的定位性能。
1 指纹库构建
1.1 指纹数据采集

1.2 分区模型构建
随着定位区域的不断增大,算法的计算复杂度不断增加,分区是减小计算复杂度行之有效的方法。HE等[13]对比在大型场景中不同分类方法的精度和效率,采用OVRSVM模型在办公区域构建分区的定位误差较小。根据物理连通性将目标区域划分为K个子区域,需要对数据S训练出K个支持向量机模型,第i个支持向量机模型转化为求解如下最优化问题:
(1)

φi(s)=(wi)Ts+bi,i=1,2,…,K。
(2)
在线阶段将测试点输入到K个决策函数中,根据k=arg max(φi(st)),i=1,2,…,K,得出测试点隶属分区Ck。
1.3 分区数据的校正

f(l)~GP(m(l),k(l,l*)) ,
(3)
其中,m(l)=E(f(l)),为均值函数;K(l,l*)=E[(f(l)-m(l))(f(l*)-m(l*))T],为协方差函数,通常使用核函数作为协方差函数。设定训练集L对应的输出为f,测试集L*对应的输出为f*,建立多维高斯分布进行估计:
(4)
对上述式中f*求取边缘概率得高斯分布的均值和方差,进而求得预测值:
f*∣L*,y,L~N(μ*,Σ*) ,
(5)
(6)
其中,
(7)
(8)
判断RPi对于APj的接收信号强度数据是否需要校正:
(9)
其中,κ为预定义因子,rij表示st中对于APj的接收信号强度值。如果该式成立,则进行校正,该接收信号强度数据为
(10)
其中,λ为校正权重,以减小接入点信号波动的影响。
2 基于信号双尺度的加权近邻定位算法
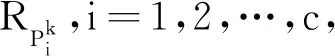
2.1 基于信号相似度的近邻算法

(11)

(12)

(13)

2.2 基于信号差异值的动态近邻算法
(14)

传统方法是手动设定近邻点数目c,但由实际分析可知,最优c值并不是固定的,不同时间、场景中的最优c值是变化的,因此需要设定动态c。笔者提出一种基于环境噪声的动态k近邻方法,定义环境参数为γ用于对近邻程度的判断:
(15)
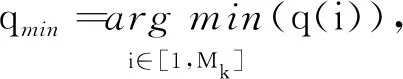
2.3 基于Blending的信号双尺度加权近邻算法
(16)

Blending算法是一种模型融合算法,分为均匀融合和线性融合。该文采用线性加权融合方法,对不同的分类模型之间的差异设置不同的权重值,完成分类模型之间的互补,实现更好的分类效果。定义最小化误差函数为
(17)


图1 信号双尺度算法框图
从图1可知,指纹数据分为训练集和测试集。训练集用于训练算法模型,测试集则用于算法性能测试。算法包含离线阶段和在线阶段。离线阶段分为分区模型和GPR校正模型的训练,并依据验证集得出最优权重值。在线阶段则依据离线阶段训练得出的模型和最优权值实现测试点的位置估计。
3 实验分析
3.1 实验配置
实验场景为江南大学物联网工程学院C区一楼环形走廊Ω1和C106房间Ω2,以区域相邻边作为x和y轴,以1 m×1 m为采集密度采集接收信号强度,每个参考点采集5次。根据采集的蓝牙信标的信号衰减趋势,在Ω1中每4 m处布置一个蓝牙信标作为接入点。场景细节描述为:环形走廊Ω1=50 m×40 m,划分为4个分区,如图2(a)所示,每个分区放置10个接入点,共获得1 320组数据,其中792组数据用于训练集,528组数据用于测试和验证。房间场景Ω2=9 m×7 m,如图2(b)所示,小区域划分为4个区域,可以有效提高定位精度,房间内放置10个接入点,共获得400组数组,其中240组作为训练集,160组用于测试和验证。
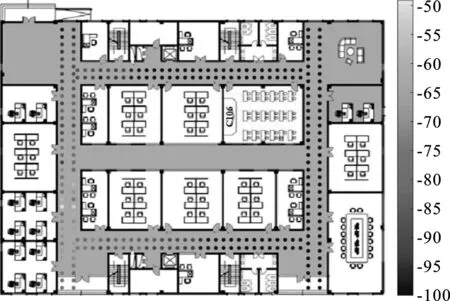
(a) 环形走廊信号分布
实验数据采集是基于蓝牙的指纹定位技术,接入点采用的是基于NRF52832的低功耗蓝牙信标,布置间距设置为4 m。离线采集阶段使用Android端BluetoothGet软件,在参考点采集数据时进行10次滤波,减小接收信号强度的波动。为提高指纹库的有效性,选择人员走动较少时采集接收信号强度数据。在线仿真阶段采用Pycharm2019仿真软件。对提出的DGC-TSNN,与WKNN方法、相关系数法(Correlation Coefficient Method,CCM)以及Bayesian方法进行性能对比。算法的参数设置:OVRSVM的惩罚系数C=3.6,GPR模型中预定义因子κ=2,更新权重λ=0.5,信号相似度中权重ω=0.3,α1和α2由最优化问题求解得出。
3.2 分区及GPR校正精度分析
在对走廊区域Ω1和房间区域Ω2定位时,采用分区的精细化定位方式,将走廊区域划分为4个条形区域,房间内部根据物理坐标划分为4个区域,以OVRSVM构建分区模型。基于分区模型对测试集分析,各分区的分区精度如表1所示,分区判别准确率达95%以上,能够满足一般精度需求。对提出的GPR校正模型测试分析,测试Ω1环形走廊区域的4个分区,以每个分区的66组测试集进行分析,测试DGC-TSNN算法是否加入GPR校正的平均定位误差,结果如表1所示。从表1中可知,DGC-TSNN算法在Ω1的4个分区内加入GPR校正后的平均定位误差为0.40 m左右,可知GPR校正可以有效地减小异常点引起的误差。

表1 分类及校正分析
3.3 定位误差分析
定位误差分析中测试点定位误差计算采用欧氏距离计算,即计算测试集估计坐标和真实坐标之间的欧氏距离。对4种方法定位误差的均方根误差、平均绝对误差进行对比,计算公式为
(18)
(19)
其中,(xc,i,yc,i)为第i个测试点的估计坐标,(xt,i,yt,i)为第i个测试点的真实坐标。定位误差对比如表2所示,DGC-TSNN算法在Ω1走廊和Ω2房间区域有着最低的均方根误差和平均绝对误差。在Ω1走廊中的均方根误差和平均绝对误差为0.45 m左右,在Ω2中的均方根误差和平均绝对误差也均为4种方法中的最低,均在1 m以内。

表2 4种方法的误差 m
采用WKNN、CCM、Bayesian和DGC-TSNN算法对比分析,以箱型图显示4种算法的定位误差,如图3所示。从图3(a)中Ω1的误差箱型图可知,DGC-TSNN算法有着最低的误差中位线,约为0.354 7 m,定位精度最高;Bayesian次之,但是Bayesian算法的离群点较多;WKNN和CCM算法的定位精度稍差。从图3(b)中Ω2的误差箱型图可知,较于走廊区域4种方法定位精度有所降低,Ω2房间的最低误差中位线为0.263 1 m左右。由于Ω2房间区域中有较多干扰设备,易引起信号波动。相较于其他算法,DGC-TSNN算法的定位误差得到有效的降低。
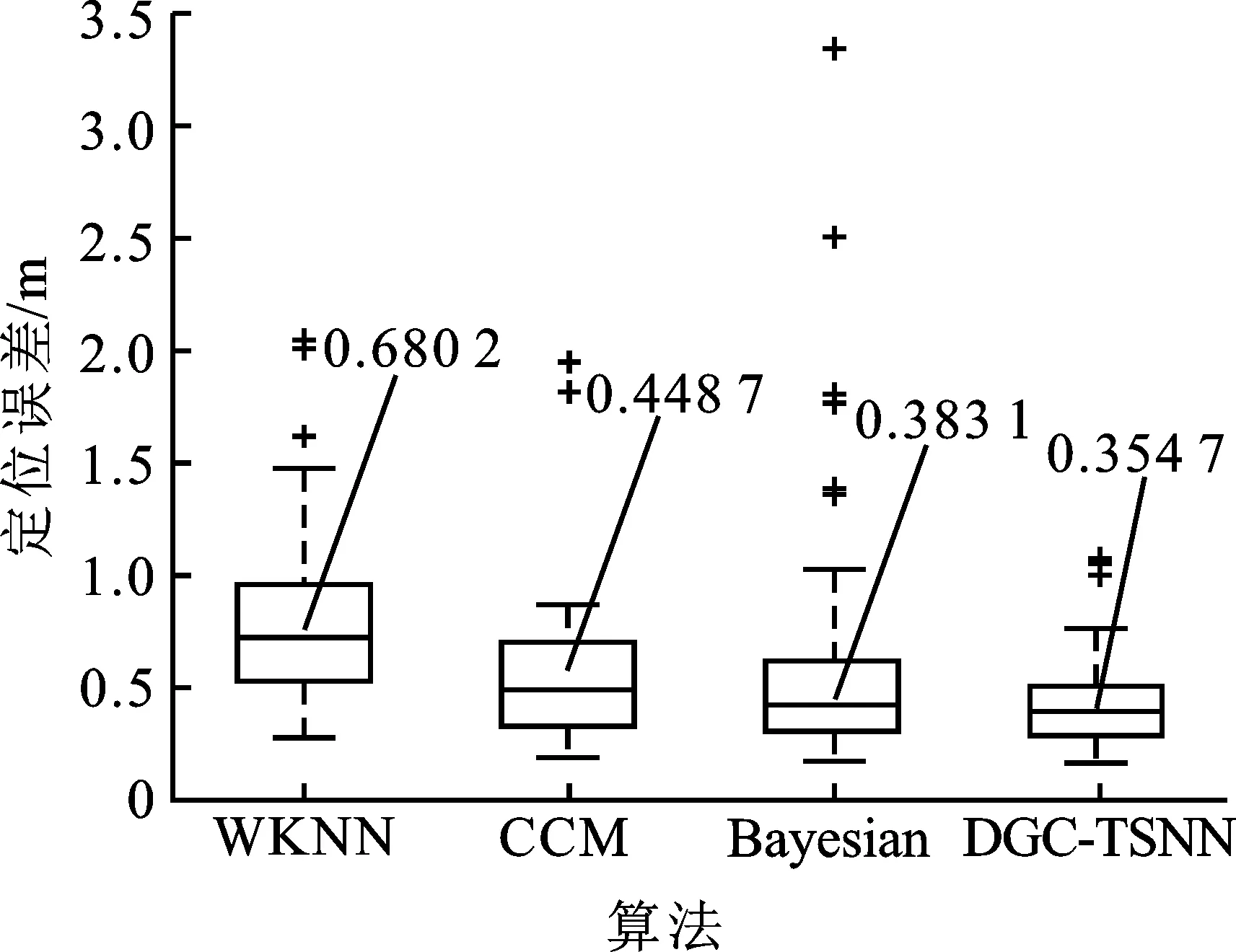
(a) 环形走廊区域Ω 1
3.4 接入点数量对定位精度的影响
在环形走廊区域Ω1和房间区域Ω2中,就接入点数目对定位精度影响进行测试分析。针对接入点数目(N=4,5,6,7,8,9,10)对WKNN、CCM、Bayesian以及DGC-TSNN算法进行测试。采用环形走廊的264组测试数据和房间内的80组测试数据进行测试分析,实验结果如图4(a)和图4(b)所示。

(a) 环形走廊区域Ω 1
从实验结果可以看出,Ω1环形走廊和Ω2房间区域的定位误差随着接入点数目N的增加而减小,且DGC-TSNN算法能够保持较低的定位误差。在Ω1中DGC-TSNN能够一直保持着较低的定位误差;在Ω2中,当N>6时,DGC-TSNN保持着最低的误差。两种区域最终N=10的平均定位误差为0.40~0.50 m。
4 结束语
笔者提出一种动态校正的信号双尺度近邻定位算法。该算法根据目标区域的物理连通性构建分区模型,以高斯过程回归训练接入点信号距离模型,预测分区路径损耗特性,校正信号波动值,引入信号相似度和信号差异值构建信号双尺度近邻定位算法,设定环境参数动态获取近邻k值,减小环境噪声。对测试结果分析可知,较于传统算法,改进算法的定位误差及计算复杂度均得到有效的降低。算法在实际应用中需先对目标区域构建离线指纹库,训练分区模型和接入点信号距离模型,并将算法部署在服务器端,以提高定位效率。
