考虑电动汽车数量影响的电网日前调度区间优化

杨 俊 琛

(国网福建省电力有限公司 漳州市龙海区供电公司, 福建 漳州 363199)

0 引 言

随着“碳达峰”与“碳中和”的“双碳”目标的提出,建设新型电力系统进程加快。大力发展清洁能源及储能技术,成为推动新型电力系统建设的动力。随着电动汽车(Electric Vehicles,EVs)的普及,现有电动汽车的数量逐渐增多,而电动汽车作为一种灵活的储能资源,对于电网调度有着巨大的潜力[1-3]。

现有研究中,对新能源的不确定性和电动汽车参与的调度优化进行了一定的研究。文献[4]中,利用区间数表示分布式电源和负荷的不确定性,将区间优化用于冷热电联供型微电网中,并采用加速的交替方向乘子法进行求解。文献[5]考虑风光出力及电、气负荷的不确定性,建立了电气互联的虚拟电厂区间优化模型,并对电动汽车集群的充电行为进行了分析。文献[6]针对综合能源系统中的新能源出力的不确定性,利用区间优化进行分析。文献[7]在考虑了风电的不确定性区间波动的基础上,从风电并网规模的角度分析了储能对电网运行的影响。文献[8]根据区间运算规则,建立了风电出力不确定性下的电动汽车充电站的区间优化模型,重点考虑了EV充电功率对充电站的影响。文献[9]对电价不确定性进行区间表示后,对电动汽车聚合商的影响进行了分析。文献[10]定义了弃风系数的有效区间,采用教与学算法解决含风电区间不确定性的优化模型。文献[11]在传统安全约束经济调度基础上,以区间优化为基础构建含风电出力不确定的线性区间优化模型。文献[12]针对光伏、风电、冷热电负荷随机性问题,以区间理论为依据,建立非线性区间优化模型,结合改进粒子群算法进行求解。从现有研究而言,对电力系统中风电的不确定性和电动汽车参与的调度优化进行了一定研究。但现有研究大都从电动汽车的充电功率、集群分析等角度进行,较少从电动汽车的不同数量对电网的影响进行分析。

因此,本文提出了一种考虑电动汽车数量影响的电力系统日前调度优化模型。首先,考虑不同数量电动汽车对电网调度优化的影响,构建相应模型;进而,利用区间数学将风电的出力不确定性表示为区间数,建立含风电出力不确定性的区间优化模型;最后,将区间优化模型转换为两个子模型,即乐观模型和悲观模型进行求解。在10机组模型上验证模型的准确性与经济性,表明所提方法的优势,同时为电网调度人员提供一定的指导。

1 电网日前区间优化模型

1.1 不确定变量区间表示

风电的出力不确定性使得电网调度优化存在一定的难度。本文中风电出力的不确定性采用区间形式表示。在区间数学中,区间数为一堆有序实数:

[P]=[P-,P+]={x|P-≤x≤P+}

(1)

式中:P-、P+——区间的下限、上限。

因而,将电网中风电出力的不确定性利用风电出力上下限进行表示:

(2)

式中: [Pw,t]——t时刻风电出力;

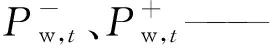
1.2 电动汽车数量影响

随着“双碳”目标的提出,新型电力系统中电动汽车的数量逐渐增多。电动汽车的潜力还未得到充分发掘。同时电动汽车参与调度的数量对电网优化运行也存在较大的影响。

在每个时刻,电动汽车参与电网调度优化的数量需要满足约束:

(3)

式中: Numevc,t、Numevd,t——时刻t电动汽车充电、放电数量;

Numevc,t,max、Numevd,t,max——时刻t电动汽车可充电、可放电的数量最大值。

由于电动汽车需要足够的充电时间,所以需要限制其放电时间,从而电动汽车才能保留足够的能量来满足车主未来的出行需求。电动汽车的总充电和放电持续时间应受到限制[13]:

(4)

(5)

式中: Δtc、Δtd——电动汽车的平均充、放电时间;

Numevc,max、Numevd,max——可供充、放电的电动汽车总数;

T——调度总时长。

1.3 日前模型

1.3.1 目标函数

在电网运行优化中,为了提升电网运行经济性,以机组运行成本F1、排放成本F2、机组启停成本F3及车主充电成本F4为目标函数,则

minF=F1+F2+F3+F4

(6)

机组运行成本F1为

(7)

式中:Pi,t——机组i在时刻t的出力;

ai、bi、ci——机组i的燃料成本系数。

机组运行成本为二次函数,不易直接求解,因此在本文中对其进行线性化处理[14]。

排放成本F2为

(8)

式中:ρ——煤中灰尘的平均重量百分比,默认值为20;

μ——灰尘与PM 2.5的换算系数,默认值为5.1;

η——减排效率,默认值为99%。

αi、βi、χi——机组i的煤耗系数[15-16],机组的排放量与其煤耗成正比。

机组启停成本F3为

(9)

Hi,off=Ti,off+Ti,c

(10)

式中:Si,h——机组i的热启动费用;

Si,c——机组i的冷启动费用;

Xi,off,t——机组i在时刻t的连续离线时间;

Ti,off——机组i的最小停机时间;

Hi,off——过渡时刻;

Ti,c——机组i的冷启动时间。

车主充电成本F4代表所有电动汽车用户的财务成本,计算方法为收费成本减去放电收入,即

F4=pevc,tNumevc,tPevc,tΔt-pevd,tNumevd,tPevd,tΔt

(11)

式中:pevc,t、pevd,t——在时刻t的充、放电的电价。

1.3.2 约束条件

在对电网调度进行优化时,在任何时刻需要满足供需平衡。

功率平衡约束为

Pi,t+Pevd,tNumevd,t+Pw,n,t=Pd,t+Pevc,tNumevc,t

(12)

式中:Pd,t——时刻t的负荷值。

风电出力约束为

0≤[Pw,t]≤Pw,t,max

(13)

式中:Pw,t——时刻t风电的出力;

Pw,t,max——时刻t风电的最大出力。

旋转备用约束:

(14)

式中:Pi,max——机组i的最大出力;

Rt——时刻t的系统预留要求。

机组上、下限约束为

Pi,min≤Pi,t≤Pi,max

(15)

式中:Pi,min、Pi,max——机组i的最小出力、最大出力。

机组爬坡约束为

-Rd,t≤Pi,t-Pi-1,t≤Ru,t

(16)

式中:Rd,t、Ru,t——机组i的下爬坡、上爬坡速率。

机组启停时间约束:

(17)

式中:Ti,on、Ti,off——机组i的最短在线时间和最短离线时间;

Xi,on,t、Xi,off,t——机组i在时刻t保持连续在线和离线的持续时间。

2 区间运算转换

区间数学中,可以根据区间数进行区间运算:

[A]+[B]=[A-+B-,A++B+]

(18)

[A]-[B]=[A--B+,A+-B-]

(19)

由于风电出力的不确定性利用区间数进行表示,因此得到的目标函数也为区间形式。

[F]=[F-,F+]=〈Fc,Fw〉

(20)

式中:Fc,Fw——目标函数中点和半径值。

(21)

(22)

可以利用目标函数区间中点和区间半径值来判断目标函数的优劣。同时需要基于不确定目标函数区间来计算其中点和半径。此处,通过两次优化过程求解不确定目标函数的区间[14]，即

F-=minF

(23)

F+=maxF

(24)

3 算例分析

3.1 算例参数设置

本文采用10机组系统进行算例验证,其中包括一个110 MW的风电场。负荷曲线如图1所示,10机组参数使用文献[15]中参数[16-18]。假设旋转备用需求为负荷需求的10%,总调度时长为24 h。

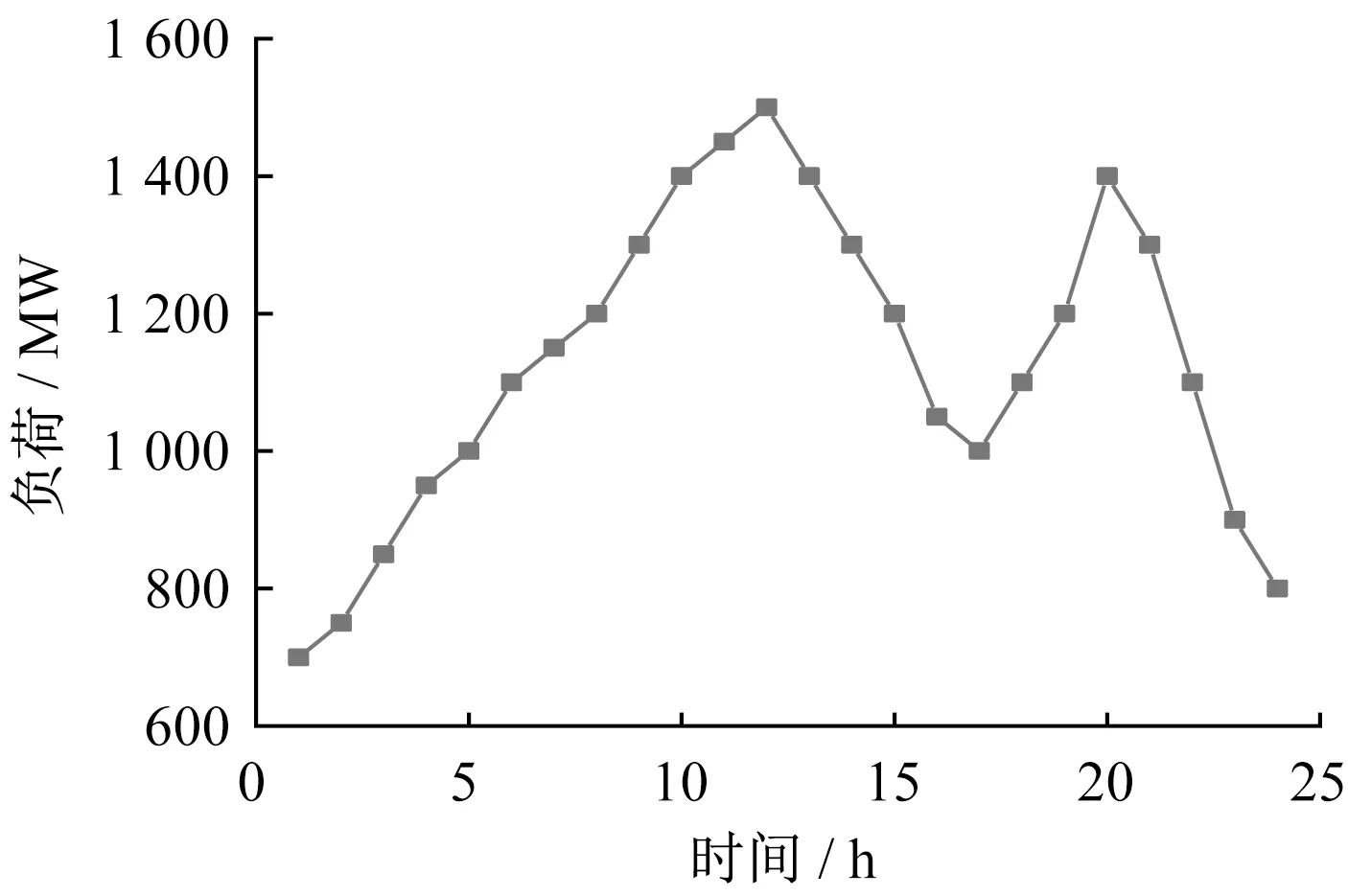
图1 负荷曲线

电动汽车的平均充放电功率均为1.8 kW。充放电频率均为每天一次。设定在每个时间段可供充电和放电的电动汽车的最大数量是不发生改变的。设定每个时刻可用于充、放电的电动汽车百分比分别设置为95%和40%。PM 2.5排放处理成本为18 990.6元/t。

风电出力的不确定性区间范围利用风电预测值的百分比叠加得到。在本文中分别设置10%、20%预测值叠加风电原始预测值得到风电出力的不确定性区间范围。风电出力区间如图2所示。

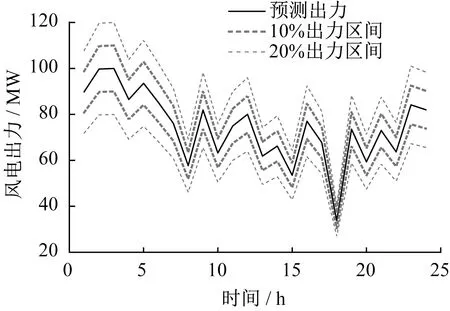
图2 风电出力区间

3.2 不同电动汽车数量下的对比

为了分析不同数量的电动汽车对电网调度优化的影响,设置如下场景进行分析。

场景1:考虑风电出力的不确定性,电网中不含有电动汽车;

场景2:考虑风电出力的不确定性,电网中含有50 000辆电动汽车;

场景3:考虑风电出力的不确定性,电网中含有100 000辆电动汽车;

场景4:不考虑风电出力的不确定性,电网中不含有电动汽车;

场景5:不考虑风电出力的不确定性,电网中含有50 000辆电动汽车;

场景6:不考虑风电出力的不确定性,电网中含有100 000辆电动汽车。

场景1～场景3为含风电出力不确定性下不同数量的电动汽车,而场景4～场景6为确定性情况下不同数量的电动汽车。利用所建立的模型,分别求解场景1～场景6,得到结果。不确定性情况下调度结果如表1所示;确定性情况下调度结果如表2所示。

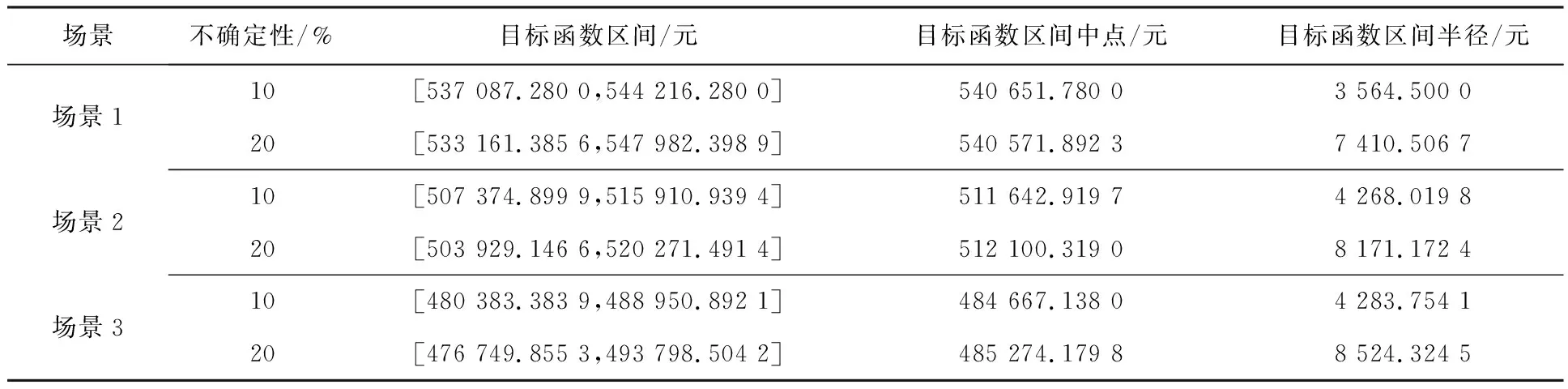
表1 不确定性情况下调度结果

表2 确定性情况下调度结果

由表1可见,不确定性范围区间的增大,使结果区间范围也增大。同时,所得到的区间中点值较为接近,而区间半径值相差较大。因此,在区间范围发生较大变化时,得到的目标函数区间范围及其优劣也将发生较大改变。

在同样的不确定性程度下(如均为10%预测值叠加得到出力区间范围),若不考虑电动汽车作为一种可调资源,此时电网优化的成本费用最高。主要是因为负荷需求全部由机组承担,在凌晨低谷时风电的高出力并未得到充分利用,使得费用较高。在加入电动汽车后,总费用降低。在场景3中电动汽车数量最多的情况下,总费用最低。在随着电动汽车数量的增加,总费用降低,呈现出反相关的趋势。虽然在场景3中20%不确定性情况下的区间半径最大,但总体而言,在电动汽车数量最多的情况下,目标函数更优。

在不考虑风电出力的不确定性的情况下,场景6中电动汽车数量最多,总费用最低。此种情况也验证了不确定性情况下结果的正确性。同时在不考虑不确定性的结果中,均被包括在所得到的区间结果范围中。

因此,以场景2中20%的不确定性进行分析。为了分析不同数量的电动汽车参与情况下,以场景3中20%不确定性下机组出力进行对比分析。场景2中机组出力如图3所示;场景3中机组出力如图4所示;不同时刻电动汽车充放电数量如图5所示;电动汽车充放电功率如图6所示。图3～图6为区间上限子模型结果。

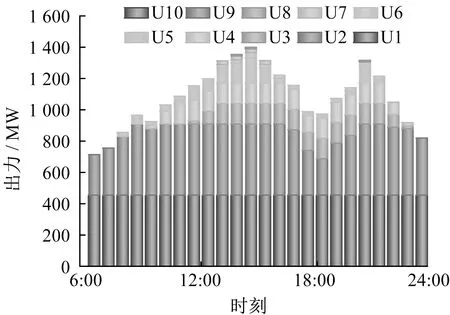
图3 场景2中机组出力

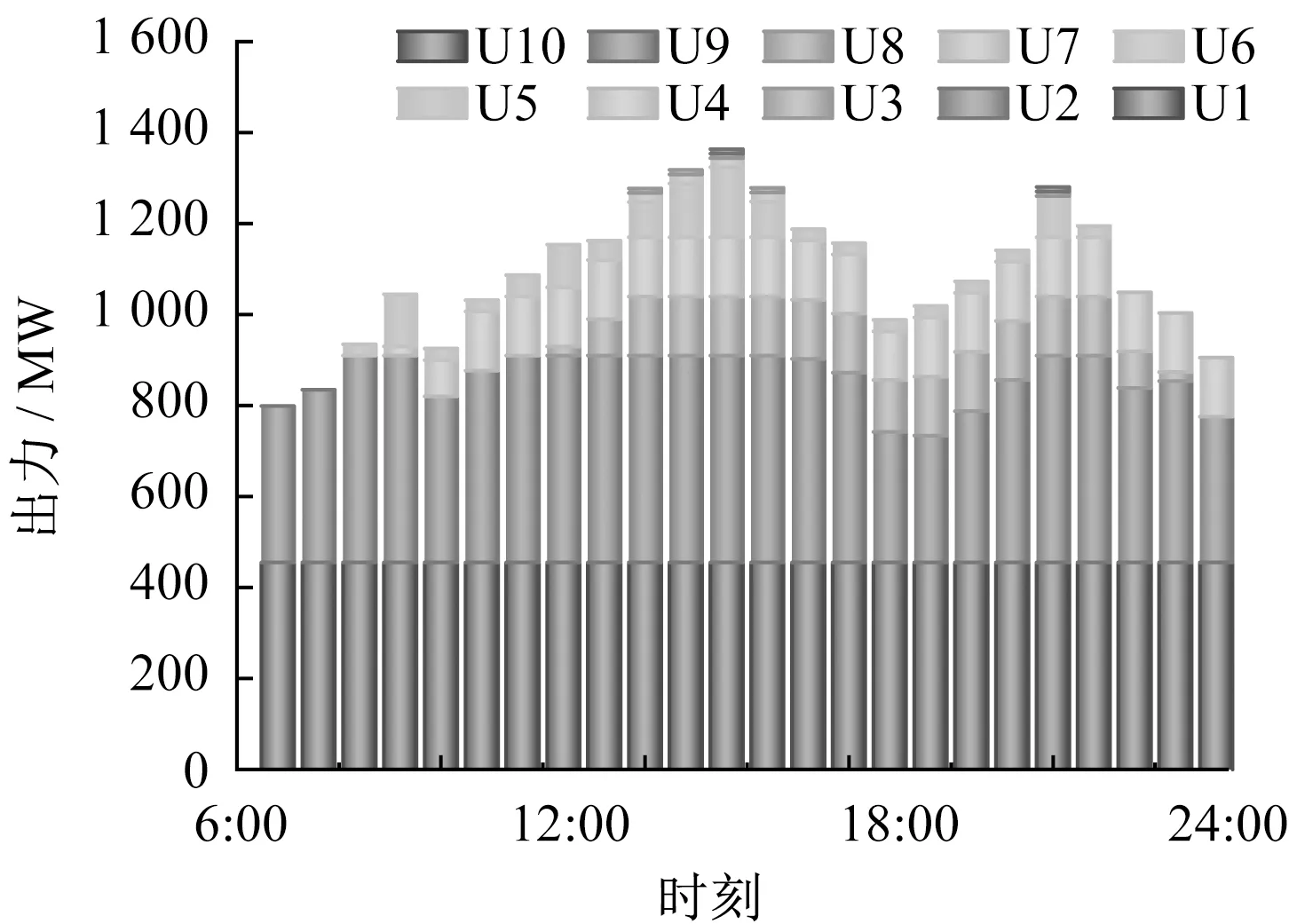
图4 场景3中机组出力

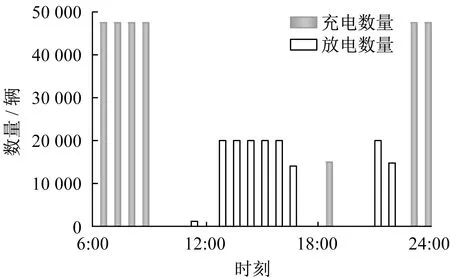
图5 不同时刻电动汽车充放电数量

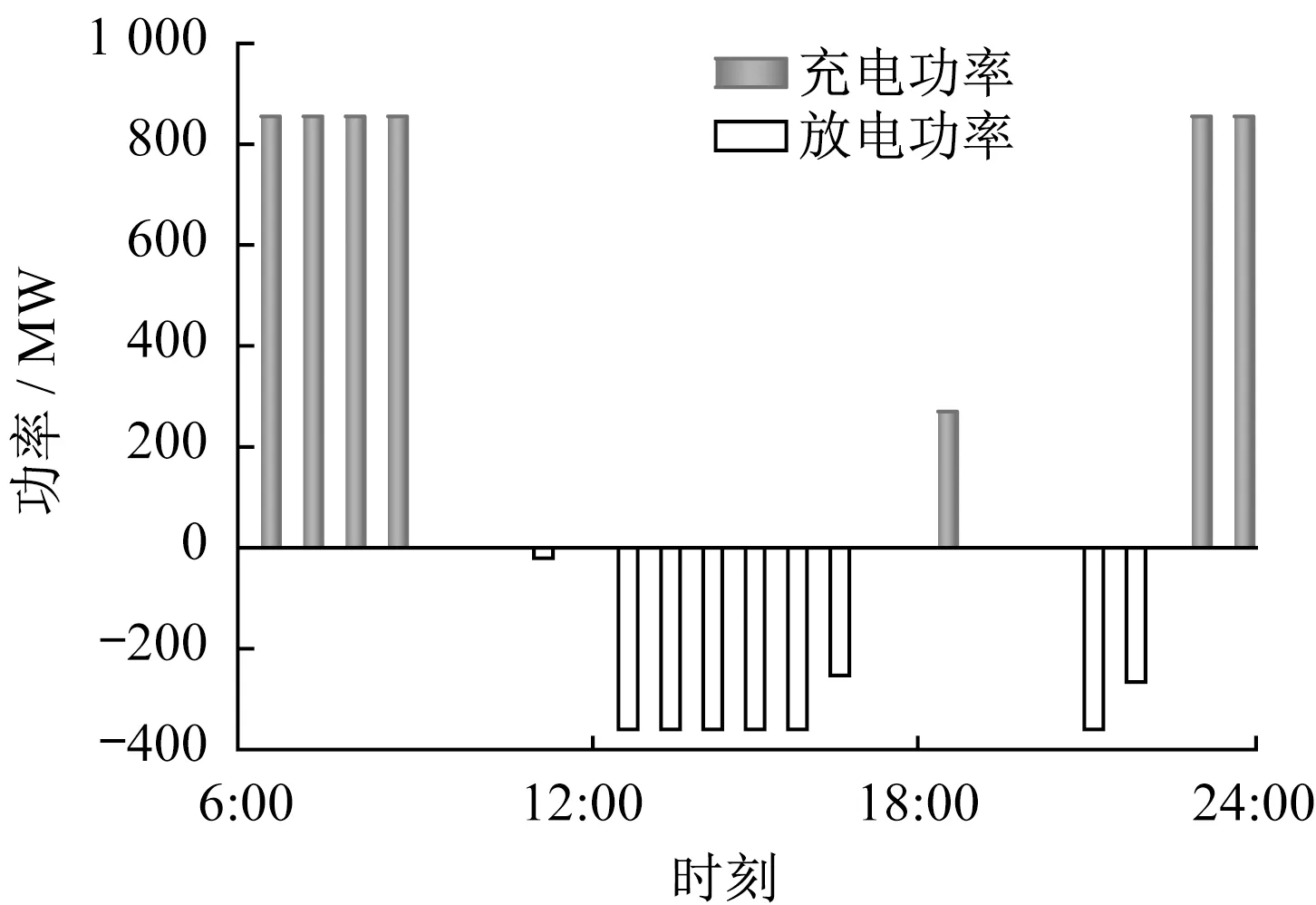
图6 电动汽车充放电功率

由图3和图4可知,在场景3中机组出力较少。相对于场景2中,场景3中的机组U2出力减少。同时在场景2中,机组U7还存在较少出力。而场景3中的机组U7并未出力。产生此种现象的主要原因是因为在场景3中电动汽车数量较多,提供了较多的出力,在负荷低谷时充电,在负荷高峰时进行放电,从而减少机组出力,降低系统运行总费用。在负荷低谷时,电动汽车充电,机组出力增多,并且将凌晨风电加以利用,从而使得新能源利用率升高。

由图5和图6可知,电动汽车充电数量较多时段主要集中于负荷低谷阶段,电动汽车放电主要集中在负荷午间高峰。这样能够较好地实现削峰填谷,提升能源利用率,发挥电动汽车充当灵活储能装置的优势及其潜力。

4 结 语

本文考虑了电动汽车的不同数量对电网日前调度优化的影响。通过将新能源出力的不确定性表示为区间形式,构建含电动汽车的电网日前调度区间优化模型,并利用区间理论,将日前区间优化模型转为两个子模型进行求解。

在考虑电动汽车参与的情况下,能够有效降低负荷峰谷差,进行削峰填谷,提高新能源的利用率。

在不含电动汽车的调度优化中,电网调度成本最高。在电动汽车数量不断增加时,电网调度总成本不断减少,提升电网运行的经济性。

在接下来的电网日前调度优化中,可调度的电动汽车数量与电网调度的关系需要进一步研究。同时对于新能源出力的不确定性和负荷的不确定性,如何利用区间优化理论进行分析是接下来的研究重点。