基于Logistic回归模型网球男子单打运动员不同盘次制胜因素分析

2022-07-04欧阳高煌李品芳陈建才

体育科技文献通报 2022年6期

欧阳高煌，李品芳，陈建才

随着网球运动在全世界的广泛传播，全球各地网球技术发展越来越科学完善，优秀网球球员的训练更加先进系统，使得网球秀男子单打运动员对各种技术和战术用也趋向多样化发展。要获得胜利首先需要掌握比赛制胜的主要影响因素，这样才能占得主动地位提高比赛的胜率，由于不同在比赛情境运动员技战术表现的多样性，因此影响运动员比赛制胜因素也各式各样，研究者当下对优秀网球运动员不同盘次比赛的赛制胜因素研就更有必要性。

查阅近年关键分的文献期刊，运用Logistic回归模型对制胜分的研究还是仅仅停留在每一场比赛制胜因素的研究，现有的网球项目对整场制胜因素研究中，运用的统计和分析方法也是多种多样，得出的制胜指标也是不一样的。有研究者运用Logistic回归模型分别对温布尔登网球和大利澳亚网球公开赛，优秀男子单打运动员整场比赛进行制胜因素研究分析，得出破发成功率、一发得分率、接发成功率、二发得分率这五项数据是制胜关键影响因素[1-2]，通过阅读这些相关文献发现，得出的结果结论分析都是大同小异，都没有脱离以整场比赛为对象的研究大框架，从而不能精确的分析优秀运动员在不同情境下比赛中制胜因素，研究的结果都只停留在表面层次，从不同盘次对制胜因素来进一步研究可能更精确的反映运动员不同情境下的经济水平，参考价值和创新更进一步。

本研究将“Logistic回归模型”和“不同盘次”引入到网球比赛制胜因素的研究中，在前人对整场比赛研究的基础上，将比赛分为不同盘次进行更加细化的研究，每一盘比赛运动员竞技表现和心理状态都存在着一定的差异，从而分析网球优秀男子单运动员在不同盘次比赛中技术和战术运用特点的差异，为我国教练员指导优秀网球运动员针对不同盘次调整训练内容、制定针对性比赛策略提供借鉴。

1 研究对象与方法

1.1 研究对象

以2021澳大利亚网球公开赛男子单打运动员不同盘次制胜因素为研究对象。

1.2 研究方法

1.2.1 文献资料

通过图书馆阅读关于网球制胜因素影响的文献和书籍，还通过百度、中国知网和中国硕博期刊网查找“Logistic回归模型”“单打”“制胜因素”“网球”“盘次”相关文献。为研究不同盘次制胜因素间的关系、数据统计方法选择以及统计结果分析提供理论支撑。

1.2.2 数据来源与指标

通过澳大利亚网球公开赛网官网网站搜集所需研究数据指标，查阅相关文献选取相应指标并与网球方向的专家学者进行交流，确定本课题研究的研究指标。统计指标如下：ACE球（X1）、双误（X2）、一发进区率（X3）、一发得分率（X4）、二发得分率（X5）、破发成功率（X6）、上网得分率（X7）、非受迫性失误（X8）、接发非受迫性失误（X9）、最快发球速度（X10）、第一发球平均速度（X11）、第二发球平均速度（X12）、接发球成功数（X13）、接一发球得分（X14）、接二发接得分（X15）等15个变量分第一盘、第二盘和决胜盘进行分类统计。

1.2.3 数据处理

1.运用Excel2016对指标进行梳理，运用SPSS25.0各项变量指标进行相关度分析，了解各项制胜因素之间的相关度。然后再进行柯尔莫可洛夫-斯米洛夫检验（K-S检验）对筛选指标为正态分布的进行独立样本t检验，被筛选的其他指标进行非参数检验，了解各项预选自变量是否可以明显的区分因变量（胜、负），最后将各项相关性不强的预选变量导入Logistic回归模型进一步分析。

2.构建Logistic回归模型本文研究优秀网球男子单打运动员在澳网公开赛中比赛每盘（第一盘、第二盘和决胜盘）的胜负（Z）与制胜因素（X）之间的变量关系。因变量为运动员比赛的胜负是一个二分类变量（1或0），胜方表示“1”，负方表示“0”，自变量为各种影响比赛胜利的制胜因素，这种情况下运用Logistic回归模型进行分析最为合适。因此可以通过研究优秀网球运动员多种制胜因素（X）的作用下对比赛胜负（Z）发生概率P（0，1），得出运动员比赛胜负概率P于自变量（X）的关系。

Logistic回归模型：设P为选手胜的概率，则1-P为选手负的概率，P取值为（0，1），其中，b0为常数项；b1、b2……bn称为回归系数。

Logistic回归公式：

将以上回归方程变换，就能推导出

同时根据式（2）得到

其中，a=b0+b1X1+b2X2+…+bmXm

2 研究结果

2.1 优秀网球运动员不同盘次制胜因素预选变量的相关性分析

对优秀男子单打运动员不同盘次比赛中制胜因素预选变量进行相关分析，为了减小Logistic回归模型分析筛选得出数据结果的误差。其中数据显示如果｜r｜值靠近1，表明制胜因素预选变量间的相关程度越高，越趋向于0预选变量间的相关程度越无关，一般来说相关度被分为低、中、高三个等级，｜r｜＜0.4相关性为低级；0.4≤｜r｜＜0.7为中相关性；0.7≤｜r｜为高相关性（何文盛2011）。

如表1所示，ACE球与第一发球平均速度呈显著性相关P小于0.05，r值为0.435，存在中级相关性；最快发球速度与第一发球平均速度和都呈显著性相关P小于0.01，r系数分别为0.730和0.487，最快发球速度与第一发球平均速度存在高度相关，最快发球速度与第二发球平均速度存在中度相关性；第一发球平均速度与第二发球平均速度呈显著性相关P小于0.01，r系数为0.581存在中度相关性；接发球成功与接一发球得分和接二发接得分都呈显著性正相关P小于0.01，r系数分别为0.737和0.643，接发球成功与接一发球得分存在高度相关性，接发球成功与接二发接得分存在中级相关性。本文研究相关性0.5≤｜r｜时，两个预选指标之间存在高度相关性，因此经过筛选将X12、X14、X15等三个指标被剔除。通过相关性分析最后筛选剩下13项预选指标之间不存在高度的线性关系。

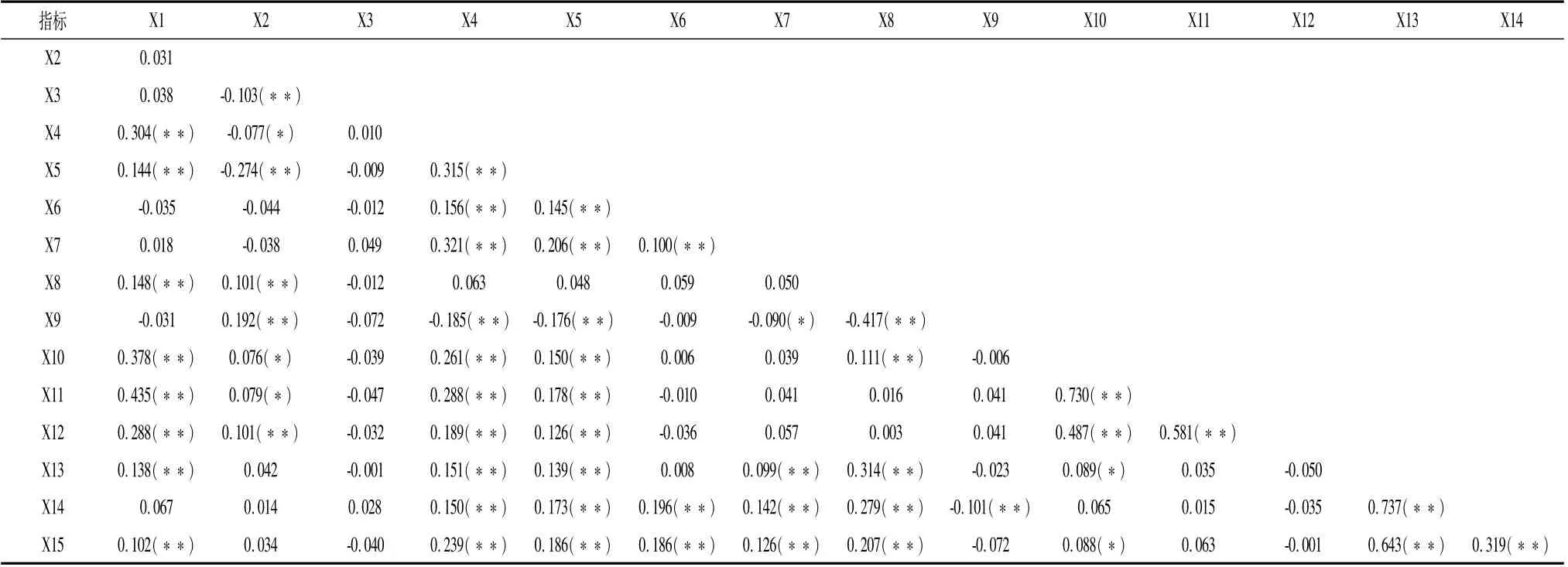
表1 优秀男子单打运动员制胜因素预选变量相关性分析

2.2 优秀网球运动员不同盘次制胜因素数据的柯尔莫可洛夫-斯米洛夫检验

进行柯尔莫可洛夫-斯米洛夫检验的主要想看预选指标是否属于正态分布，为确保下一步数据分析的准确性，将所有预选指标导入柯尔莫可洛夫-斯米洛夫检验。相关结果如表2显示第一盘变量X1、X2、X4、X6、X7、X8、X9、X10、X11、X13的显著性水平P＜0.05，说明都不符合正态分布。除了这些预选指标其他指标的P值均大于0.05，因此只有X3和X5呈正态分布。第二盘变量X1、X2、X3、X4、X6、X7、X8、X9、X10、X13的显著性水平P＜0.05，说明都不符合正态分布。除了这些预选指标其他变指标显著性P值大于0.05，因此只有X5、X10和X11呈正态分布。决胜盘变量X1、X2、X5、X6、X7、X8、X9、X10、X11、X13的显著性水平P＜0.05，说明都不符合正态分布。除了这些预选指标其他指标P值大于0.05，因此只有X3、X4和X10和呈正态分布。

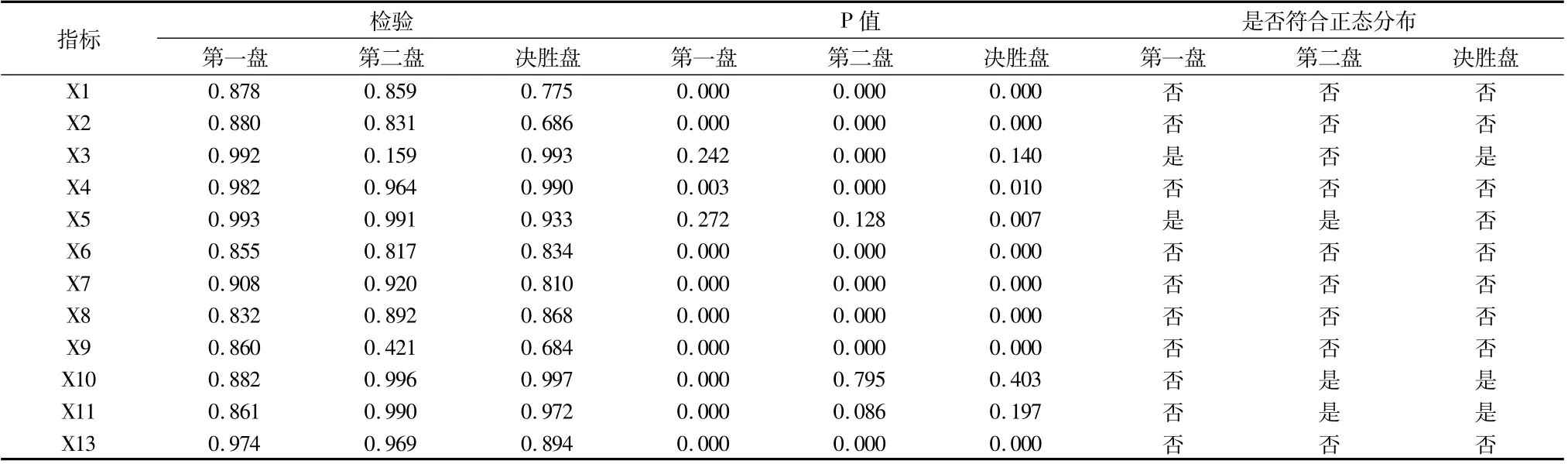
表2 变量正态分布检验总表

2.3 运动员不同盘次制胜因素非参数检验

非参数检验的主要功能对不同盘次不符合正态分布预选变量进行分析，判断预选变量对胜方和负方两组是否存在一样的区别力，避免数据作用效果重叠得出结论更加精确。如表3所示，第一盘：X4、X6、X7、X8、X9、X10、X13等这7项预选变量能比较显著的反应胜负双方的差异性（P＜0.05），X1、X2、X11这3项预选变量不能明显的区分胜负双方；第二盘：X1、X2、X3、X4、X6、X7、X8、X9、X13等这9项预选变量能比较显著的反应胜负双方的差异性（P＜0.05）；决胜盘：X1、X2、X4、X5、X6、X7、X8、X13等这8项预选指标能比较明显的反映胜负双方的不同（P＜0.05），X9不能明显的区分胜负双方。

表3 Kruskal-Wallis检验结果

2.4 运动员不同盘次制胜因素独立样本t检验

独立样本t检验主要功能对不同盘次符合正态分布预选变量进行分析，判断预选指标是否能明显地反应胜负双方的不同，避免数据作用效果重叠得出结论更加精确。如表4所示，第一盘：X3、X5这两项数据P值均小于0.05明显区分胜方与负方的不同；第二盘：X5、X10、X11，这三项数据P值均小于0.05明显区分胜方与负方的不同；决胜盘：X3、X10、X11这三项数据P值均小于0.05明显区分胜方与负方的不同。

表4 不同盘次预选变量独立T检验结果

2.5 运动员不同盘次制胜因素Logistic回归分析

进过筛选最后得到不同盘次制胜因素，表5是优秀网球运动员不同盘次制胜因素的判断结果。将自变量系数代入二项Logistic回归模型（2）回归方程中得到网球运动员制胜因素模型。

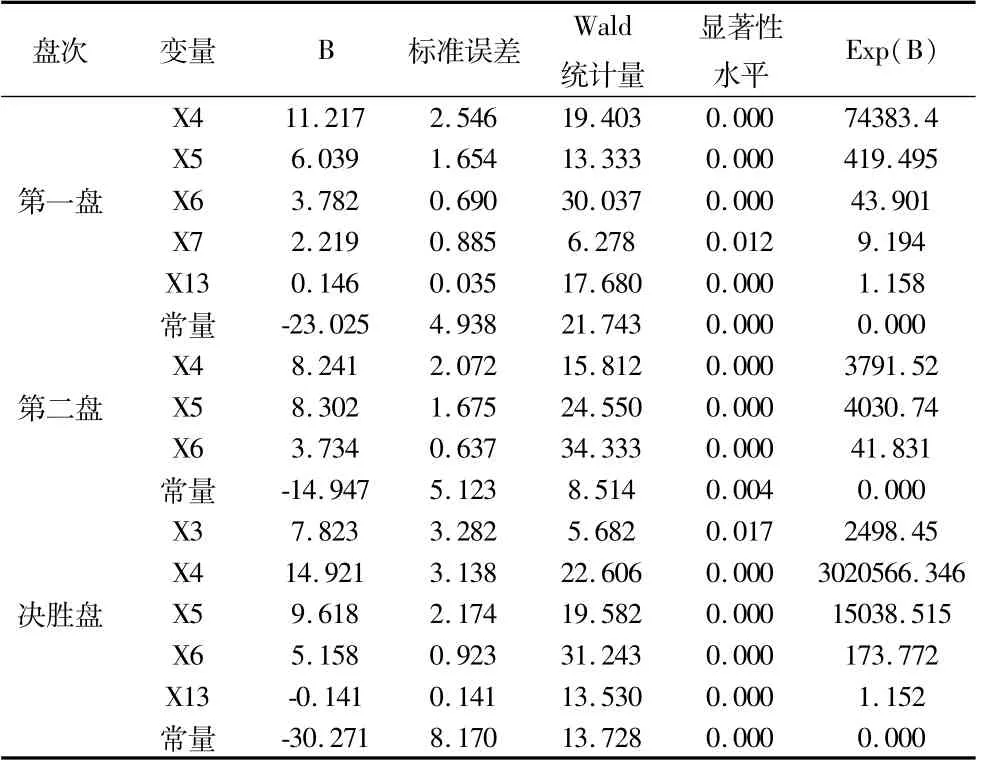
表5 优秀男子网球运动员制胜因素判断结果

第一盘：Logistic（P1）=-23.025+11.217X4+6.039X5+3.782X6+2.219X7+0.146X13

第二盘：Logistic（P2）=-14.947+8.241X4+8.302X5+3.734X6

决胜盘：Logistic（P3）=-30.271+7.823X3+14.921X4+9.618X5+5.158X6+0.141X13

在第一盘比赛，进过筛选最后得出对比赛胜利影响度由高到低依次为：（X4）、（X5）、（X6）、（X7）、（X13）。其中X6对运动员第一盘比赛胜负的影响最大，X6每提升上一个单位运动员获胜概率就提高90.1%；X13对运动员第一盘比赛胜负的影响最小，X13每提升一个单位运动员获胜概率就提高15.8%；X5每提升上一个单位运动员获胜概率就提高49.5%；X4每提升上一个单位运动员获胜概率就提高43%；X7每提升上一个单位运动员获胜概率就提高19.4%。

在第二盘比赛，进过筛选最后得出对比赛胜利影响度由高到低依次为：X4、X5、X6。其中X6对运动员第二盘比赛胜负的影响最大，X6每提升上一个单位运动员获胜概率就提高83.1%；X4对运动员第二盘比赛胜负的影响最小，“X4”每提升一个单位运动员获胜概率就提高52.1%；X5每提升上一个单位运动员获胜概率就提高73.9%。

在决胜盘比赛，进过筛选最后得出对比赛制胜具有高度影响且能反应胜负显著性的X4、X5、X6、X3、X13。其中X6对运动员决胜盘比赛胜负的影响最大，X6每提上升一个单位运动员获胜概率就提高77.2%；X13对运动员第一盘比赛胜负的影响最小，X13每提升一个单位运动员获胜概率就提高15.2%；X5每提升上一个单位运动员获胜概率就提高51.5%；X3每提升上一个单位运动员获胜概率就提高44.5%；X4每提升上一个单位运动员获胜概率就提高34.5%。

3 分析与讨论

将Logistic回归模型大部分都是运用在医学和经济学领域，也有学者将其引入到网球项目中都是对整场比赛大环境下的制胜研究，所以本文采用Logistic回归模型分析每盘比赛制胜因素是实施可行的。

研究结果得出，不同盘次比赛制胜因素种类和影响程度有一定的差异。在不同盘次“破发成功率”对比赛制胜影响最大。

1.盘次间X6影响程度对比第一盘＞决胜盘＞第二盘；X13在不同盘次对比赛制胜影响最是最小，但不能忽视这一点，接对手发球时本来就是处于被动地位的，如果能够保证有良好的接发成功率的那就说明运动员的防守能力很高，接发成功是防守反击中最关键的一点，运动员想要取得破发取得比赛胜利，最首要的就是有良好的接发成功数。

2.不同盘次X13影响大小对比第一盘＞决胜盘，X6和X13其都是反映了运动员接发球技术的运用能力和面对对手发球进攻能够有效的防守能力，体现出运动员的反应速度、灵敏等素质的优越性，由于第一盘比赛对于参赛双方都是一种进入比赛状态和试探对手打法的准备阶段，比赛强度一般都比较适中对运动员身体机能和心理压力较缓和，运动员对接发技术能更充分的展现出来。

3.X4、X5和X13这三项指标都是反映运动员发球能力，发球在比赛过程中就是代表作主动进攻，从而对比赛制胜起着关键性的作用。X4、X5和X3在不同盘次影响程度分别是第二盘＞第一盘、第二盘＞决胜盘＞第一盘和决胜盘，其中X3只出现在决胜盘发球进区率和发球质量之间是存在强烈的负相关性的，因为在决胜盘参赛双方都已经是处于最激烈的阶段比赛成败就此一盘的关键时候，比赛强度达到了最高对运动员身体机能和心理压力变成了一种对自我的挑战。运动员在决胜盘中舍弃了一发质量，来提升一发进区率，所以X3成为决胜盘制胜因素。第一第二盘X4、X5反映了运动员最佳状态发球技术应用能力，在相对紧张的状态下肢体力量、平衡、柔韧、速度等身体素质的综合体现，能成为制胜关键因素之一，那是因为运动员心理和身体机能还处于一个良好的状态，有资本去提高发球质量来追求比赛制胜。

4.X7反映了运动员在比赛中反应运动员上网得分能力，和技战术的多样性的表现。X7是第一盘独有的制胜因素。根据不同盘次关键制胜指标可以看出，运动员技能多样性的重要性，需要根据不同盘次身体机能和心理状态进行技战术的调整，这样看来不同盘次制胜因素对技战术的表现多样化是更加占制胜优势的，要求运动员从传统的底线型打法向全面型打法发展。

我们在网球不同盘次制胜因素分析中，结合Logistic模型进行分析筛选指标，将网球整场比赛进行细化分成不同盘次进行串联分析，能将优秀网球运动员在不同盘次下竞技表现和心理差异更详细的体现出来。在本研究中数据量太小了，如果数据量能更大从温网、法网、美网结合，可以将模型构建得更细致一些。如果从不同场地不同盘次研究制胜可能会更高一点，这样就能排排除场地影响带来的误差。