不定方程x3±2 197=26y2的整数解

李改利，高 丽，戴妍百，李秀秀

（延安大学数学与计算机科学学院，陕西延安 716000）

不定方程

是一类重要的三次不定方程，关于该不定方程的整数解已有不少的研究成果［1-12］，其研究的内容主要集中 在a = 1，2，3，4，5，6，7，10，11，15，29。1942 年，LJUNGGREN［1］证明了当a = 2，D > 2，D无平方因子且不能被3或6k + 1型素数整除时，方程（1）最多只有一组正整数解；之后赵天［2］利用唯一分解定理证明了当a = ±1，D = 2 时，方程（1）仅有正整数解(x，y) =(1，1)，(23，78)；高丽等［3］证明了当a = 1，D =1 043 时，方程（1）仅有整数解(x，y) =( - 1，0)；宋晓禹等［4］证明了当a = -1，D = 749时，方程（1）仅有整数解(x，y) =(1，0)；张洪等［5］利用递归数列、同余式性质以及Pell 方程解的性质证明了当a = 2，D = 43时，方程（1）仅有整数解(x，y) =( - 2，0)，(14，± 8)；张娟等［6］利用同余式和递归数列的方法分别证明了当a = 2，D = 273 时，方程（1）仅有整数解(x，y) =( - 2，0)，(34，12)，当a = 3，D = 182时，方程（1）仅有整数解(x，y) =( - 3，0)，(51，27)；李恒等［7］利用同余、Legendre 符号的性质以及初等数论方法给出了当a = ±3，D = pq 时，方程（1）的整数解；李双娥［8］证明了当a = -3，D = 26 时，方程（1）仅有整数解(x，y) =(3，0)；郑爱琳［9］证明了当a = ±4，D = 73时，方程（1）仅有整数解(x，y) =(4，0)；杜先存等［10］给出了当a = ±5，D = 6q 时，方程（1）的整数解；张洪［11］证明了当a = -7，D = 1 时，方程（1）仅有整数解(x，y) =(7，0)，(8，± 13)，(14，± 49)，(28，± 147)，( 1 54，± 1 911) ，当a = 7，D = 1 时，方程（1）仅有整数解(x，y) =( - 7，0)，(21，± 98)；高丽等［12］给出了当a=11，D=2pq，即为奇素数且p ≡13(mod 24)，q ≡19( )mod 24 时，方程（1）的整数解。当a = 13 时，方程（1）的整数解仍未得到解决。

本文在阅读相关文献［1-12］的基础上，利用同余式性质等初等数论的方法，证明了当a = 13，D = 26时，不定方程x3+ 2 197 = 26y2仅有正整数解(x，y) =(13，13)，(299，1 014)，不定方程x3- 2 197 = 26y2仅有整数解(x，y) =(13，0)。

1 相关引理

引理1［13］不定方程

仅有正整数解(x，y) =(1，1)，(23，78)。

不定方程

仅有整数解(x，y) =(1，0)。

2 主要结果

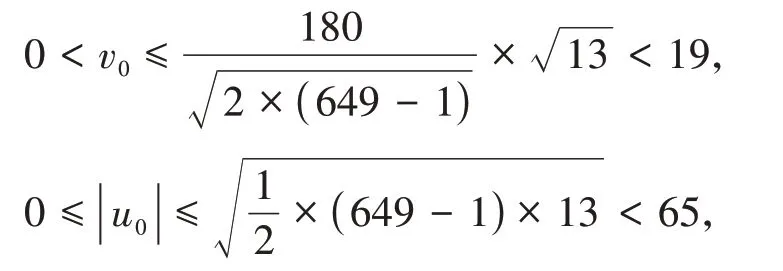
逐一验证可得(2x + 13)2- 13(2b)2=-507都无整数解。因此该种情形下无满足不定方程x3+ 2 197 =26y2的整数解。得证。

3 结语

本文利用同余式性质等初等数论的方法，证明了不定方程x3+ 2 197 = 26y2仅有正整数解(x，y) =(13，13)，(299，1 014)，不定方程x3- 2 197 = 26y2仅有整数解(x，y) =(13，0)。

对于不定方程x3± a3= Dy2尚未得到其一般解法，今后可以继续对a = 13时方程x3± a3= Dy2的整数解进行研究，找到D 符合不同取值情况时方程的整数解，即利用不同的解决办法得到其一般解法。