大气压氩气介质阻挡放电特性的一维粒子仿真

2022-07-04孙安邦刘天旭叶书荣李昊霖

南昌大学学报（理科版） 2022年1期

孙安邦，刘天旭，叶书荣，李昊霖

(西安交通大学电气工程学院电力设备电气绝缘国家重点实验室，陕西西安 710049)

近年来，低温等离子体在材料表面改性、污染防治、生物医学等方面有着越来越多的应用。其中大气压低温等离子体的产生不需要昂贵复杂的真空设备，所以其结构简单且低成本的特点正在受到人们的重视。介质阻挡放电(dielectric barrier discharge，DBD)是大气压低温等离子体产生的一种常用方式。DBD是一种将绝缘介质插入放电空间的一种放电形式，可以在很宽的气压范围(104Pa至106Pa)与频率范围(50 Hz至1 MHz)内启动[1]，属于高气压下的非热平衡放电。在大气压下其放电外观分为丝状放电模式和均匀放电模式，前者存在大量丝状的放电通道，会产生局部的热效应，对材料表面产生一定的损伤；而后者放电现象分布在整个空间，类似汤森放电和辉光放电，不会损坏试品，非常适合于材料的处理[2]。研究表明，使用惰性气体氛围、施加气流作用等措施能有效地使介质阻挡放电向着均匀模式转变[2]。

近年来，Massine等人通过实验测量以及CCD高速摄像对大气压下氩气和氦气的介质阻挡放电中的辉光放电现象进行了研究[3]；清华大学王新新从放电理论角度出发讨论了DBD两种模式的成因，并通过实验实现了氦气和氮气的均匀模式放电[2]；空军工程大学的宋飞龙等人采用光谱诊断法研究大气压氩气介质阻挡放电特性[4]。然而，DBD尺寸小的特点给实验诊断带来了一定的困难，而且实验无法以较高的时间与空间精度揭示放电过程中的关键物理过程。因此不少研究者对DBD进行了仿真研究。Hagelaar等人使用流体模型，对大气压下氩气DBD射频放电进行了仿真工作，揭示了放电从α模式向γ模式的转变过程[5]；西安交通大学的姚聪伟等人搭建耦合了外电路与化学反应的一维流体动力学模型，对氩气DBD过程中的物理参量变化与放电过程进行了讨论[6]；李平等人建立二维轴对称流体模型，通过有限元法研究氩气在不同气压下DBD特性[7]。但由于DBD的非热平衡性，电子能量呈现非麦克斯韦分布，流体模型的描述尚不够精确。而粒子模拟直接跟踪带电粒子的运动，其物理过程是自洽的，可以提供等离子体任何详细的运动信息[8]。

本文搭建了一维PIC/MCC(Particle-in-cell/Mont Carlo Collision)模型，仿真研究了氩气在均匀模式下的DBD特性，通过耦合弹性碰撞、激发碰撞、电离碰撞以及复合等反应，实现了对放电过程的精确描述；通过使用粒子权重自适应(APM)以及基于OpenMPI的并行技术加速仿真过程，实现了500kHz正弦交流电源驱动下氩气DBD过程的仿真，探究了其时空演化特性以及外施电压、气隙间距、介质板介电常数等参数对放电特性的影响。本文与参考文献[6]的流体模型的放电形貌和物理量数值与变化趋势具有较好的一致性。

1 模型的建立

1.1 PIC/MCC模型

PIC(Particle in cell)模型通过跟踪宏粒子的运动并将宏粒子向格点的插值来获得空间物理量的分布，并通过MCC(Monte Carlo Collision)过程，引入粒子的短程碰撞，使PIC算法可以处理粒子弹性碰撞、激发、电离等过程，二者结合就是PIC/MCC模型[8]。算法流程如图1所示，图中t为仿真时刻，tend为仿真结束时刻。

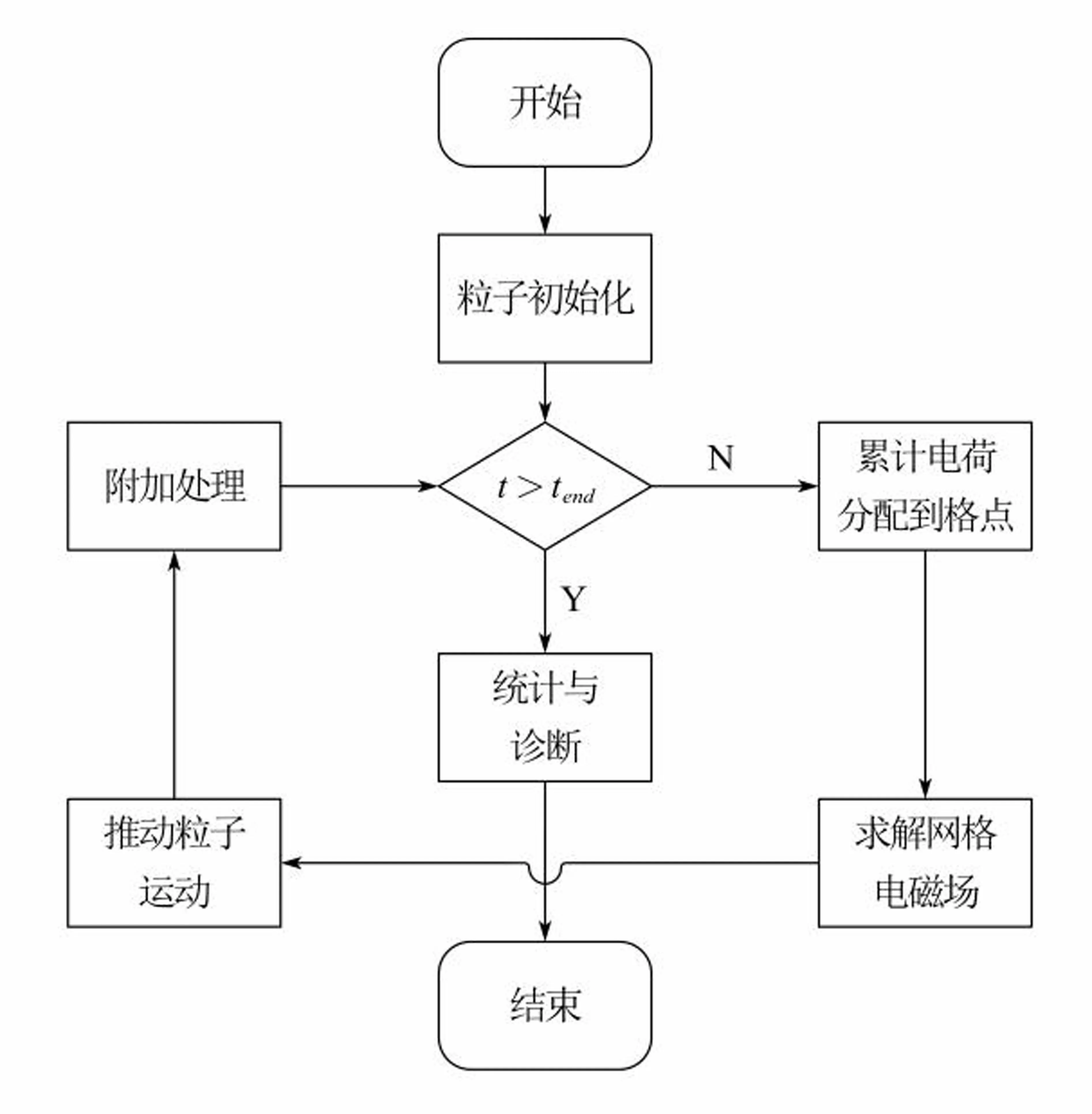
图1 PIC/MCC算法流程

首先进行粒子初始化，之后每个时间步内依次执行累积电荷、求解电磁场、推动粒子、碰撞处理(如碰撞、激发、电离、复合等过程)四个步骤[9]，最后对粒子进行统计平均得到宏观物理量。

粒子初始化中，本文假定起始时刻的电子密度与离子密度相等，均为8×1015m-3。电子与离子的位置在气隙空间均匀分布，而速度呈麦克斯韦分布。累积电荷的过程中，本文采用一阶插值函数，将带电粒子的电荷映射到相邻的两个格点之上。一维DBD结构的电场求解使用泊松方程：

(1)

其中φ表示电势，ρ表示电荷密度，ε表示介电常数，e表示元电荷量，ni与ne分别表示该点的离子数密度与电子数密度。DBD过程中，运动到介质板表面的带电粒子会附着其上，形成表面电荷。介质板表面电荷及其形成的电场对于DBD的演化过程十分重要。介质表面电荷密度σ的变化可用下式表示：

(2)

其中，Γe与Γi分别为介质板处电子与离子的通量，γ为介质表面的二次电子发射系数。

在离散的条件下，泊松方程可以写成如下格式：

(3)

其中Δx为空间格点的间距，ε为介电常数，i=1,2,...n，由左侧极板接电源正极，右侧极板接地的边界条件可知：

(4)

假设左侧与右侧的介质板与等离子体的边界的格点序号分别是d1与d2，左侧、右侧介质板的厚度分别是l1和l2，以左侧介质板为例，有：

Dd1+1/2S-Dd1-1/2S=σ1S+ρd1SΔx/2

(5)

其中Dd1-1/2和Dd1+1/2分别是边界左、右侧Δx/2处的电位移矢量，S为包围路径法向的面积，σ1为边界面介质板表面电荷密度，ρd1为紧邻边界面空间网格内的电荷密度，用格点电势表示电位移矢量，有：

(6)

其中ε0和ε1分别为真空和左侧介质板的介电常数，考虑两侧极板的边界条件，有：

(7)

同理，右侧介质板与等离子体边界处的边界条件为：

(8)

在仿真过程中等离子体区域的电场强度由外部电场与等离子体区域带电粒子的自洽电场所叠加构成，外部电场由外施电场与介质板表面电荷电场所叠加，介质板表面电荷电场对放电的发生与熄灭有着重要的影响。

假设左右介质板表面电荷面密度分布为σ1、σ2，根据高斯定理可以求得表面电荷单独作用在等离子体区域产生的电场为：

(9)

假设左、右介质板的厚度为d，其相对介电常数为ε1，气隙间距为L，加在极板上的外施电压为V(t)，左侧介质板、气隙、右侧介质板中电场强度分别为EL、EV和ER，它们满足如下关系：

(10)

可以得出外施电压单独作用在等离子体区域产生的电场为：

(11)

合成电场EO由外施电压与介质板表面电荷单独作用电场的叠加：

EO=Eσ+EV

(12)

带电粒子的运动采用velocity verlet算法，利用粒子前一时刻的位置xn、速度vn、加速度an与该时刻的加速度an+1，通过迭代得到粒子下一时刻的位置xn+1与速度vn+1[10]：

(13)

蒙特卡洛碰撞过程中考虑的电子、离子碰撞类型如表1所示。采用伪碰撞(Null Collision)[11]和相应的碰撞截面数据σ(ε)[12]来确定具体碰撞的类型。

表1 电子、离子碰撞反应类型

1.2 复合过程

本文中考虑电子与离子的复合过程，定义了粒子源项Si(m-3s-1)，表示单位时间单位体积内有Si个电子-离子对结合变成中性原子[4]。

(14)

fre代表复合反应的总数量，ne代表参与复合反应的电子数密度，ni代表参与复合反应的离子数密度，nα代表参与复合反应的中性分子数密度，而kri代表了第i个复合反应的复合系数。在每个格点Vcell的体积中，δt时间内复合的电子-离子对数量Nr为：

Nr=SiVcellδt

(15)

表2给出本文考虑的复合反应类型及复合系数，反应系数来自文献[13-17]。

表2 复合反应及系数

在氩气DBD过程中，存在Ar+和Ar2+两种离子。Ar+由电离碰撞产生，文献[6]的研究表明，由于电荷交换碰撞反应速率过高，放电之后每个时刻分子离子Ar2+的密度与总粒子密度的占比要明显高于原子离子Ar+，说明分子离子Ar2+是正离子的主要成分。说明真实物理世界中，Ar电离产生的Ar+几乎全部转化为Ar2+，即Ar2+的数密度与原本产生的Ar+是高度一致的，且二者均是带着一个正电荷，在本文中，原子离子Ar+的数密度时空分布可以等效被近似为Ar2+的数密度时空分布。

1.3 粒子权重自适应

PIC/MCC算法的程序运行时间与宏粒子数正相关。实际放电工况下带电粒子数随时间不断变动，如果宏粒子数量过多，模型求解速度极慢且消耗的内存巨大；如果宏粒子数量过少则会引入模拟噪声。本文中采用粒子自适应权重(Adapted particle management,APM)来动态调整粒子的权重以实现仿真区域中合适的粒子数量，常用的粒子合并方法有两个粒子合并成为一个粒子，即2-1，或者三个粒子合成两个粒子，即3-2等。本文采用2-1粒子合并算法，需要说明的是，虽然2-1粒子合并算法无法同时保证动量与动能守恒，但是可以通过合并速度近似相等的两个粒子来尽可能实现结果精确。文献[17]给出了具体实现过程：

首先设置每个网格内期望的粒子数Npcc，带电粒子的期望权重为：

(16)

其中n为带电粒子的数密度。对每个格点的期望权重与粒子实际权重进行比较，当粒子权重w<2/3wd时执行合并操作，首先使用k-d tree算法寻找距离同一网格内速度最接近的两个同种粒子1和2，合成的新粒子A的权重为两个旧粒子权重之和，速度随机选择合并前的一个粒子的速度，新粒子的位置由下式进行定义：

(17)

粒子权重w>1.5wd时执行分裂操作，将旧的粒子分裂成两个同种类的新粒子，每个新粒子拥有与旧粒子相同的位置、速度、加速度以及一半的权重。

1.4 并行计算

并行计算是一种能够在同一时间内执行多条指令的算法，适合快速求解大规模而复杂的计算问题。目前国内外的高性能计算机系统中，并行编程环境OpenMPI得到了广泛的应用[18]。在PIC/MCC算法中，需要逐个处理每个宏粒子的运动、碰撞等过程，适合进行并行计算处理。本文将电子、离子均匀分配到多个核心同步处理，而电荷向格点的映射以及电磁场的求解等工作则由单一核心完成，以缩短程序运行时间。

1.5 DBD模型参数与仿真参数设置

本文中介质阻挡放电的仿真区域为平行平板电极结构，如图2所示，左侧极板接正弦电压源U=Amsin(2πft)，Am为电压幅值，频率f=500 kHz，两侧极板上各覆盖厚度d1=d2=1 mm的电介质，右侧极板接地，尽管实际放电回路中的电阻、电容、电感会对极板电压波形造成一定的畸变，但本文侧重研究放电过程中的物理过程，故对模型作一定的简化，不考虑外电路的影响，即认为左侧极板电压始终等于电源电压。介质板边界条件设置为电子完全吸收，离子的二次发射系数为0.4。两侧的介质板之中的气隙充有纯氩气。空间网格与时间步长采用均匀划分方法，空间网格间距Δx=10-6m，时间步长Δt=2×10-13s。

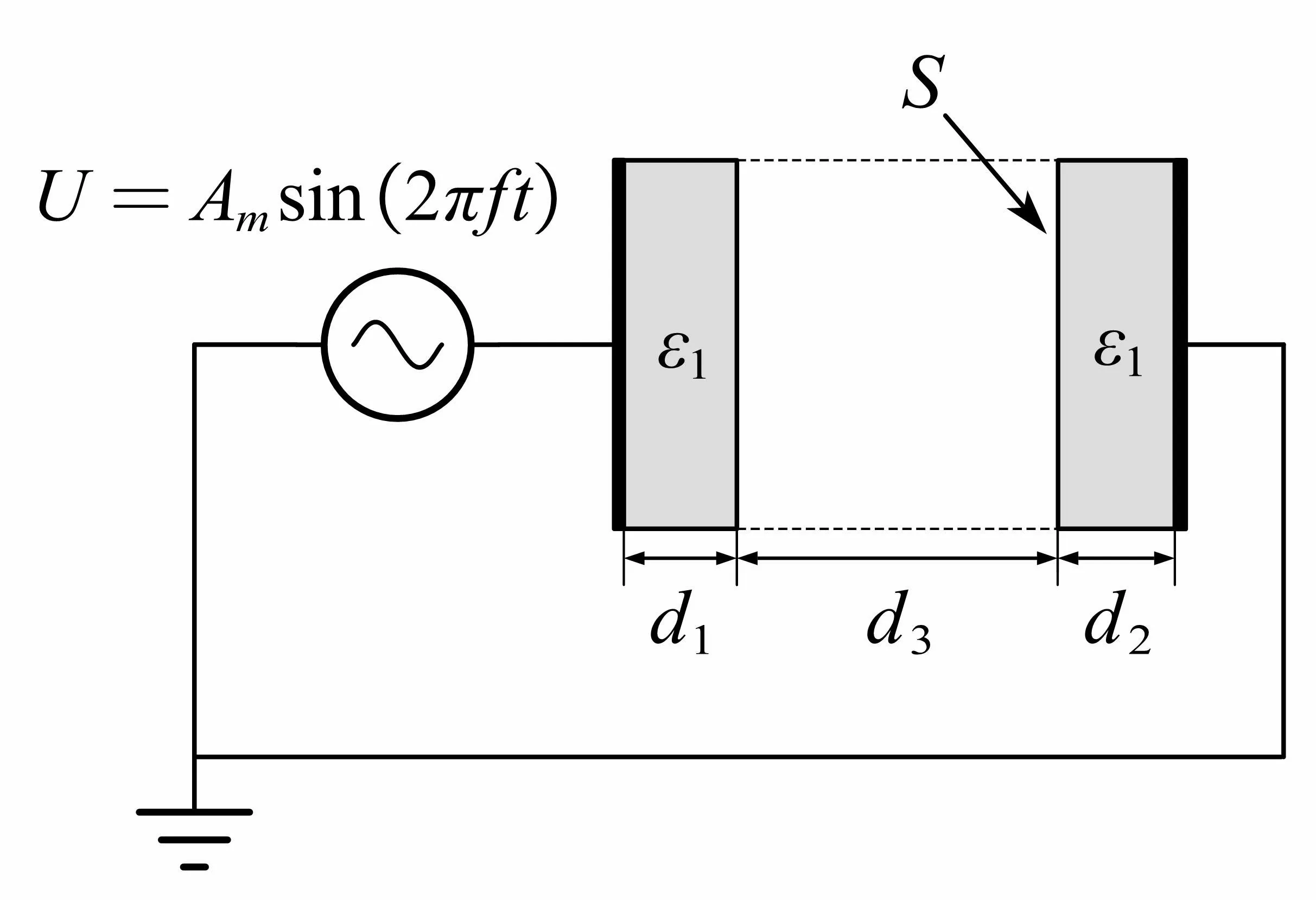
图2 仿真区域结构示意

2 结果与分析

2.1 Ar放电形貌的时空演化过程

本小节设置气体压强为1 atm，背景气体温度设定为300 K，施加的正弦电压峰值为3 kV，两介质板间隙为1 mm，介质板介电常数为4.5。仿真共持续4.5 μs，即2.25个周期，结合仿真结果分析前两周期的放电的形貌与参数特征。经实际仿真测试表明，在本文给定的工况下从第一周期负半周开始，各放电物理参量变化规律即可反应放电稳定后的状态。

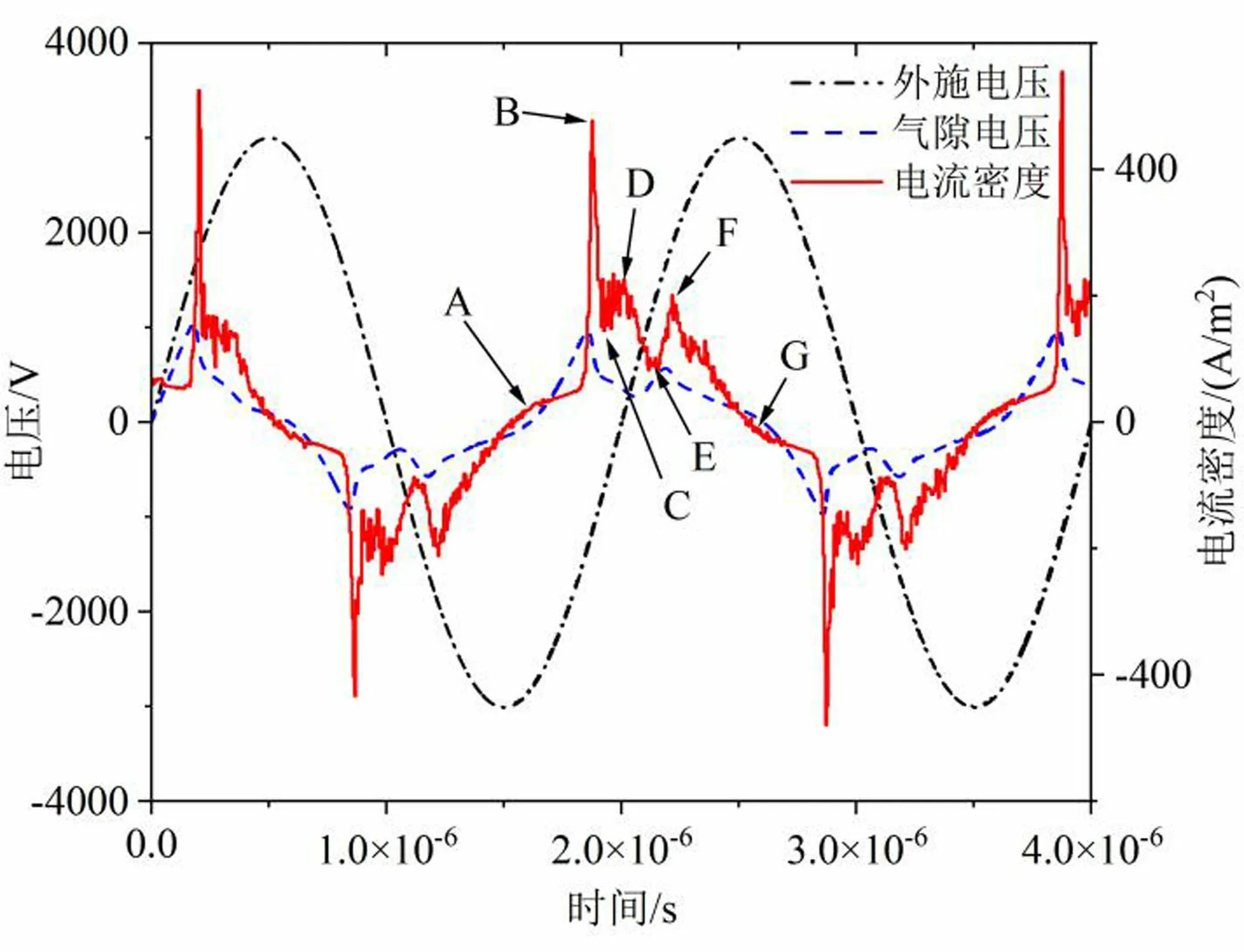
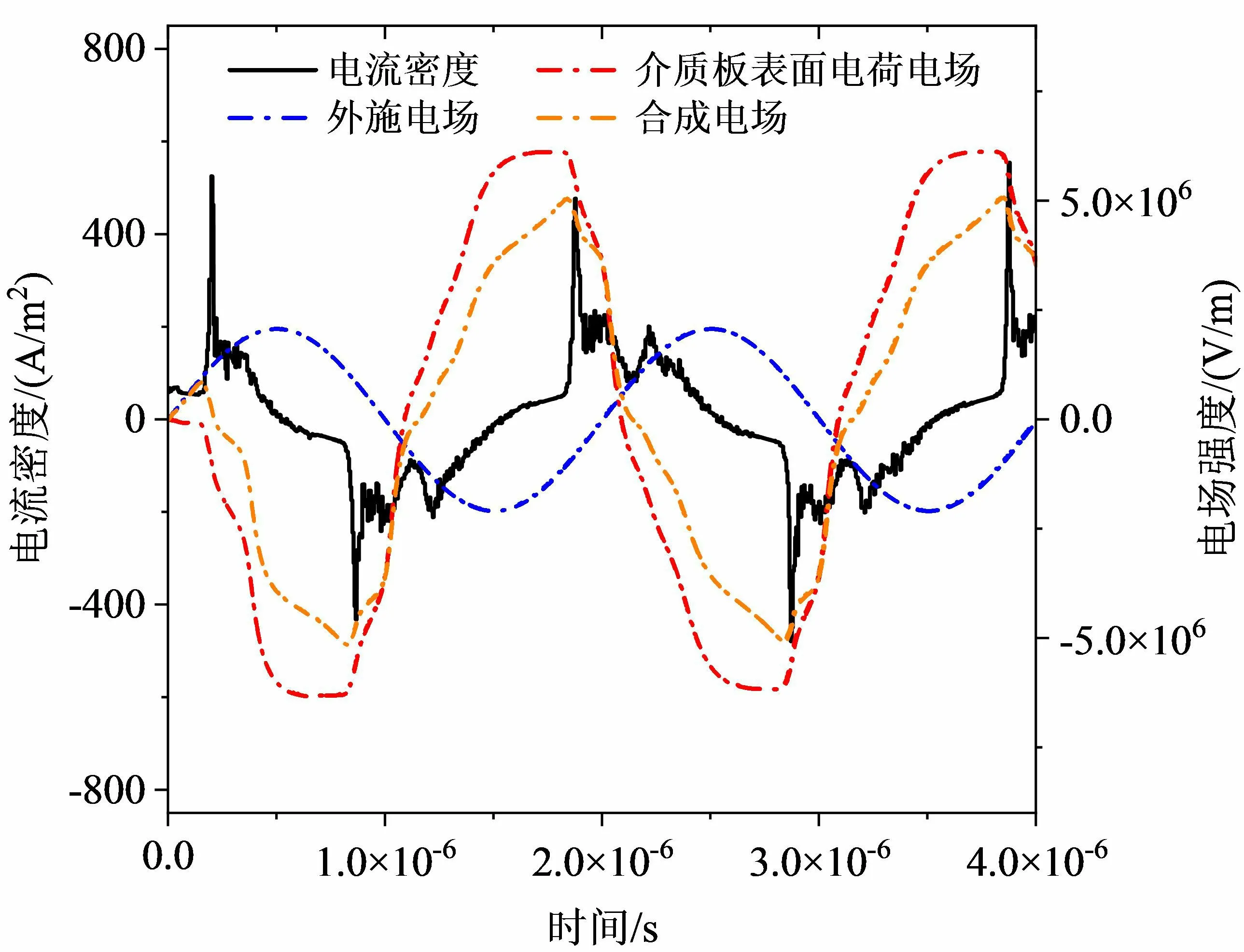
图3展示了放电过程中的极板间电流密度、气隙电压与外施电压的关系，按照放电电流密度曲线特征划分为A-G七个时刻，其具体时间与对应的放电的物理过程如表2所示，A-G阶段，左侧介质板与等离子体边界处的电势始终大于右侧介质板与等离子体边界处电势，即左侧介质板边界为阳极，右侧介质板边界为阴极。

t/s

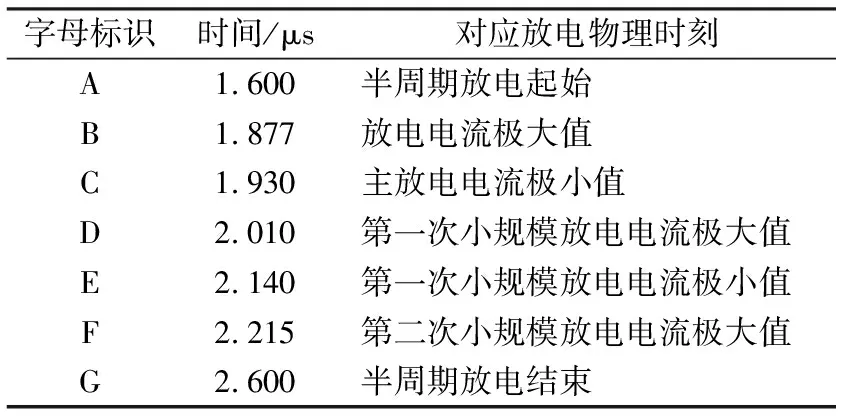
表3 不同标识对应的时间及物理过程

可以看出，每半个周期电流密度曲线有一个明显的尖峰，伴随着气隙电压的明显下降。这是因为当气隙电压升至一定数值时，产生了强烈的电子崩并引起气隙击穿，气隙中充斥着大量的带电粒子使得电导率上升，电流密度也随之上升，气隙电压也有明显的下降。但是气隙击穿后电流密度没有一直维持在一个很高的数值，而是迅速下降，这是因为放电过程中大量电荷会积聚在介质板上形成反向电场，抑制外施电压形成的正向电场，使得放电熄灭。

在后半个放电周期中，之前介质板表面积累的电荷产生的电场与外施电压产生的电场同向相叠加，会促进放电的提前发生。由此导致后续放电过程电流密度尖峰的相位提前于电压峰值约0.63π。放电电流相位变化原因是介质板表面电荷产生的电场对于外施电场在等离子体区域的影响。

从图4中可以看出介质板表面电荷电场对于放电的影响。在t=0起始时刻，两侧介质板均无电荷，外部电场与外施电场保持一致，随外施电压的升高而升高，直至发生击穿，首次主放电的电流尖峰相位落后于电压零点，此时大量带电粒子从气隙中产生并在电场的作用下向介质板运动并吸附在其表面形成介质板表面电荷，迅速形成反向电场，使得外部总电场迅速减小至零并反向增加，使正半周的放电迅速熄灭，需要说明的是，该工况下介质板表面电荷产生的最大电场的强度约为外施电场强度最大值的3倍，占外部电场的主要部分。从第一个周期的负半周开始，主放电发生于电压前半周期的下降段，超前于电压零点相位，这是正向的电场减小的过程中，对介质板表面电荷的反向电场的削弱作用减弱，从而积累出一个更强的反向外部电场，进而发生反向的击穿过程。

t/s

从图5的电子密度与图6的电子能量的时空分布可以看出，介质阻挡放电前期存在一个汤森放电的过程，从A时刻开始，电子崩从阴极向阳极发展；而之后从B时刻到D时刻，电子崩又快速从阳极发展到阴极附近，这个过程中发生强烈的电离作用，电子密度和离子密度的峰值快速增大，如图5，图7所示。之后由于介质板表面电荷的积累产生的反向电场的抑制作用，电子崩运动速度逐渐降低。而大质量的阳离子缓慢向阴极运动，在这个阶段表现为积聚在阴极附近形成鞘层结构，在鞘层区域内，电子与离子在较强的电场作用下加速，获得更高的能量。

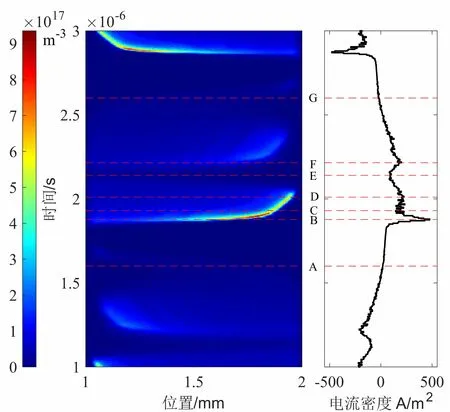
图5 电子数密度的时空演化图

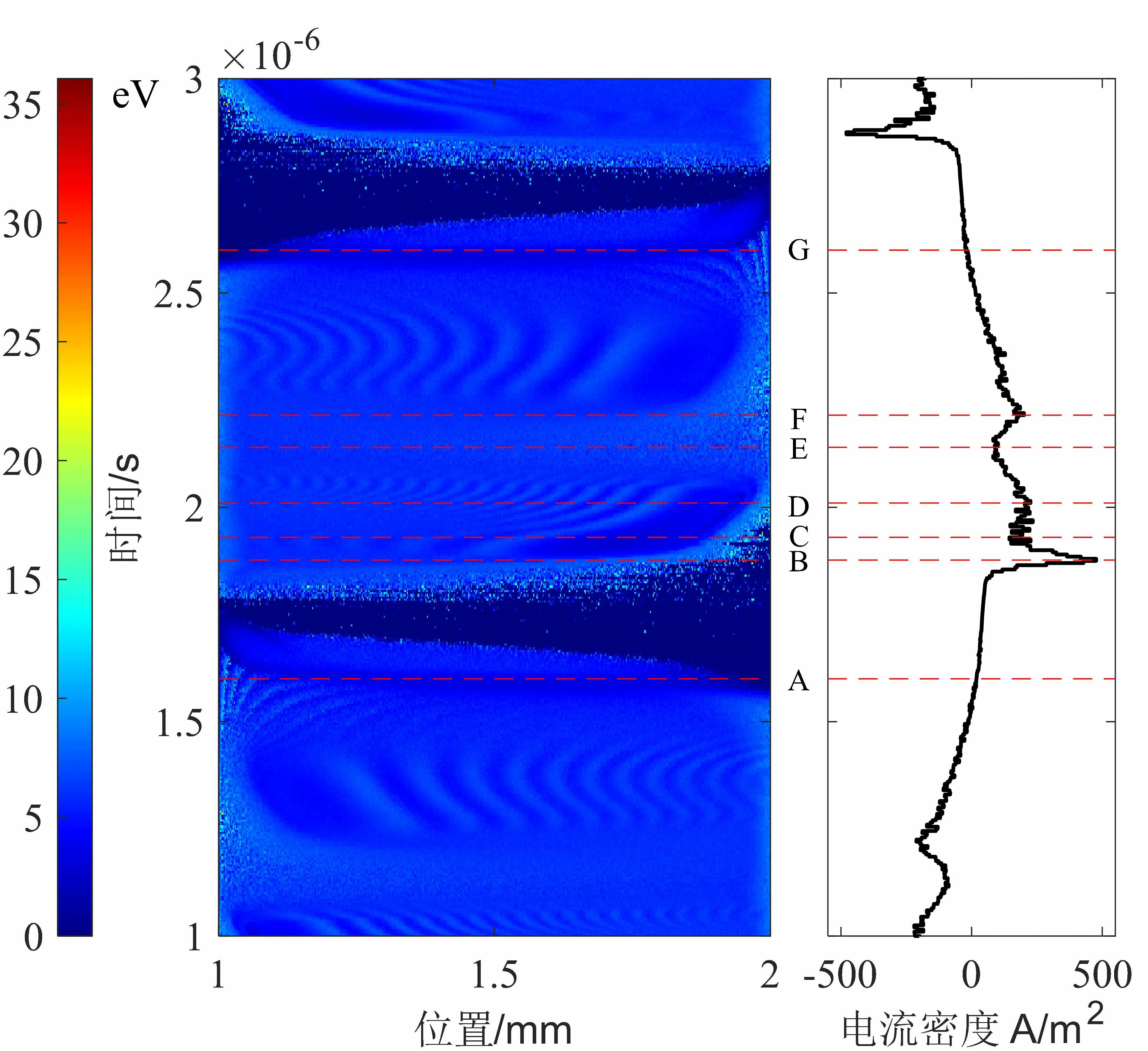
图6 电子能量的时空演化图

图7 离子数密度的时空演化图

与此同时，由于复合作用，由公式14可知，在电子与离子数密度较高的区域，复合速率较大，大量的电子和离子结合成为中性气体原子，电子离子的数密度的峰值随后快速下降。

D时刻到F时刻是一个从汤森放电到辉光放电的转化过程。此前B-D产生的主电子崩的头部位置由于强烈的电离作用产生大量的阳离子，向阴极运动一段距离之后撞击阴极介质板产生二次电子。这些二次电子在D-E时间段内在由鞘层电场加速后，这一部分高能电子向阳极运动，发生一个二次汤森放电的过程。E-F时刻，电子崩向阴极运动，和B-D过程相似，只是强度有所减弱。此后鞘层空间正电荷减少，介质板表面电荷增加，鞘层电场减弱，直到无法再建立起足够强的电子崩，放电便进入了稳定的辉光放电模式。

从F至G点属于辉光放电阶段，如图9所示，左侧等离子体正柱区的电子与离子密度几乎一致，而右侧的鞘层区域内离子密度大于电子密度。此外，左侧正柱区的电场强度相对较低，进入鞘层区域，电场强度快速升高。整个辉光放电阶段，鞘层区域的宽度较稳定，维持在0.25～0.27 mm。随着放电过程的发展，鞘层内的最大电场强度呈逐渐降低的趋势，这是因为随着电荷在介质板上的积累造成反向电场的增强，以及复合作用，鞘层内的带电粒子逐渐减少，空间场强也随之降低。

2.2 外施电压对放电特性的影响

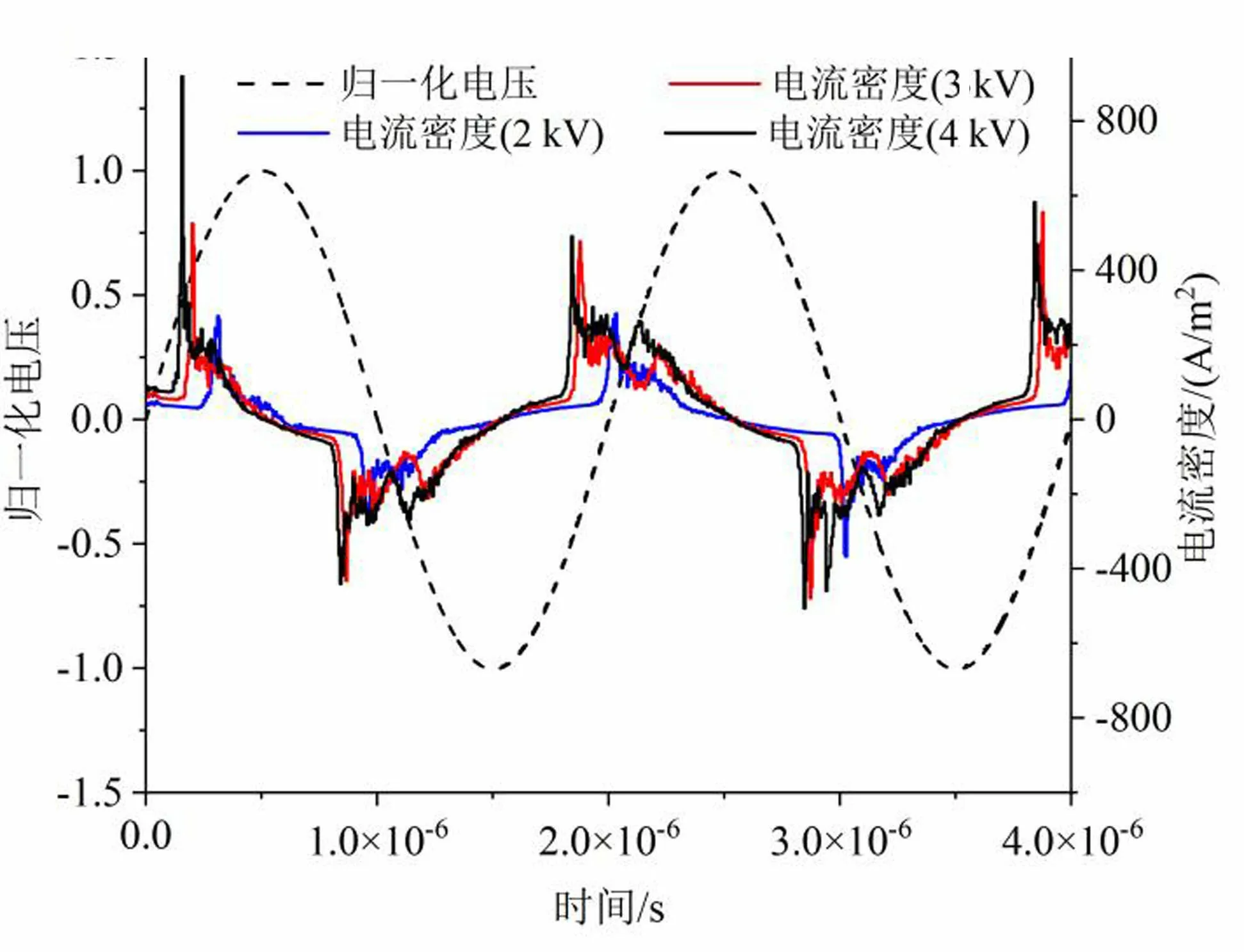
在该小节中，保持电源的频率为500 kHz不变，改变外施电压依次为2，3，4 kV。定义归一化电压为电源电压与电源电压峰值的比值，用以判别放电电流脉冲相位。从图7看，随着外施电压的升高，电流密度峰值随之升高，电流尖峰的相位随之提前。这是因为外施电压幅值越高，相同时间内电场变化越快，就能够在越短的时间内达到击穿场强引发放电；同时，更高的电压对应更大的电场强度，能够给予电场中的带电粒子更大的能量并将更多的气体电离。当外施电压为4 kV时，和外施电压为2 kV和3 kV相比，每半个周期主放电后的后续放电脉冲的峰值更大，且有明显的波动性，这是因为电压较高时带电粒子的能量较大，能够在主放电熄灭后产生更加明显的二次电子汤森放电现象，并带来一定的放电不稳定性。

t/s

2.3 气隙间距对放电特性的影响

该小节保持外施电压频率与幅值不变，改变气隙的间距依次为1、2、3 mm。从图11中可以看出，放电电流密度峰值对应的相位随着气隙间距的增大而依次滞后。

t/s

图12给出了不同气隙间距下的介质板表面电荷和外施电场情况，介质板表面电荷电场强度和外施电场强度均随间隙距离的增加而减小。在该小节的工况下，气隙间距为1和2 mm时电源电压为负值时候即发生正向击穿，而间距为3 mm时电源电压为正值时发生正向击穿。为达到击穿场强，越长的间隙越需要减弱外施电场的反向抑制作用乃至增强正向的促进作用，使放电电流的相位更加滞后。

t/s

2.4 介质板介电常数对放电特性的影响

该小节中保持电压与气隙间距不变，依次设置介质板的相对介电常数分别为4.5，8，12。从图9可以看出，放电电流的峰值随着介质板介电常数的变大而变大，而电流尖峰对应的相位随介电常数的增大而略有提前。这是因为介质板的介电常数越大，可以积累更多的表面电荷以产生更大的气隙电场，使放电能够更早发生，同时，在半周期内释放更多的介质板表面电荷也使放电电流宏观上的增大。在放电形貌上，介质板介电常数较大时，后续的放电脉冲更加明显，这是介质板间场强增大使电子能量增大所引起。