丝光沸石分子筛动态过滤清洗模型研究

邢瑞思 盛 毅 乔晓俊 张华东 张少钢

（中国石化催化剂有限公司上海分公司，上海 201507）

0 前言

丝光沸石分子筛在晶化合成时会加入氨类模板剂，虽然在反应结束后的泄压过程中除去了大部分模板剂，并采用硝酸吸收的方式进行回收利用，但是仍有部分模板剂溶解在晶化母液中，在分子筛过滤清洗时加热挥发出来，危害环境和职工健康。此外，常用的过滤清洗设备都是开放式操作，如水平带式过滤机、板框压滤机、离心机等，虽有风机排风或设备密闭等手段，但是仍不能很好地解决模板剂挥发外泄的问题。旋叶式动态过滤机在结构上与板框压滤机相似，但是在过滤机理上却截然不同，它的主要特点：1）过滤速度快，为板框式压滤机的5 倍以上且为连续操作。2）对固含量稀薄悬浮液（1%左右）可以直接过滤。3）排出滤浆固含量较高，且可调节。4）可合流和逆流冲洗。5）全自动密闭连操作，有助于有毒性物质的过滤并减少环境污染。为了更好地指导动态过滤机在丝光沸石分子筛过滤清洗过程中的应用，了解动态过滤机逐级过滤和清洗过程及物料状态，该文借助试验数据和合理假设，建立了动态过滤清洗模型。

1 旋叶式动态过滤机结构及原理

旋叶式动态过滤与传统加压过滤不同，以流体压力或离心力为过滤推动力，料浆在过滤过程中始终与过滤介质平行流动，由于料浆对过滤介质表面的剪切作用，在滤液穿过过滤介质时，过滤介质表面不积存或仅积有薄层滤饼，因此可消除或成倍减少滤饼层的阻力。

滤室内流体流动的实际工作状况是在一定流通量下，桨叶旋转带动流体并有过滤过程的流动。这种流动可以看作2种流动的叠加：一种是无流通量、无过滤过程下旋转圆盘旋转引起的流动，记为流动①；另一种是有流通量、有过滤过程但旋转圆盘静止时流体的流动，记为流动②，如图1 所示。

图1 旋叶式动态过滤机结构及过滤原理

1.1 滤室内的速度场模型

在工作状态下旋叶式动态过滤机室内流体的流动较为复杂，通常可分为边界层内流动与核心区内流动2 个部分。

一般认为，核心区的流体的径向速度与桨叶旋转所产生的转动速度相比是小量，因而这部分流体主要是以角速度旋转，其中为核心区任意半径处切向速度与旋转桨叶切向相应点切向速度的比值，它与滤室的结构尺寸、流体的物理性质及旋转桨叶的角速度相关。

式中：为进口流量；为桨叶旋转角速度；为过滤室内任一点半径；为旋转桨叶与滤饼表面的间隙；为滤室半径；为物料密度；、、、、为系数，分别与设备参数、进料流量、试验转速、滤板面积及物料密度有关，须试验过程中测定。

滤室内流体工作时大都处于湍流状态。因此对湍流运动方程进行简化：1）滤室的几何尺寸相对较小，忽略重力的影响；2）流体的运动为轴对称运动；3）边界层内黏性力与惯性力同阶；4）边界层厚度较滤室半径小得多，即/是一小量。并假设固定壁面边界层内的流体符合1/7 次幂定律，公式如下。

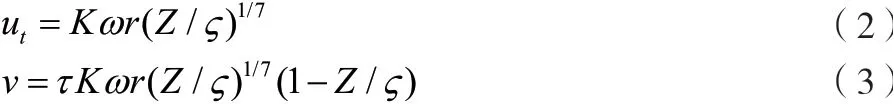
式中：为系数；为桨叶旋转角速度；为过滤室内任一点半径；为滤室内任一点到滤饼表面的距离；为边界层厚度；u、为流体的切向和径向速度。

滤室前端与后端的压力差及上一级进料流量是压力过滤推动力的主要来源，过滤阻力应包括过滤介质阻力R、滤饼阻力R和流体流动阻力R过滤速率=d/d=Δ/（μR）。在每级过滤过滤面上任一点处的过滤速度如公式（4）所示。

因此，在整个过滤面上的平均过滤速度如公式（5）所示。

式中：为每级过滤过滤面上任一点处的过滤速度。（注：\表示在任意两个半径中进行积分，是积分公式，无须特别说明）。

过滤速度不仅受操作条件的影响，而且与进料速度有关。

1.2 物料平衡

按照过滤和加水清洗2 种方式进行分类对物料进行衡算，在分析其进出料过程后，其过滤和清洗模型如图2 所示。

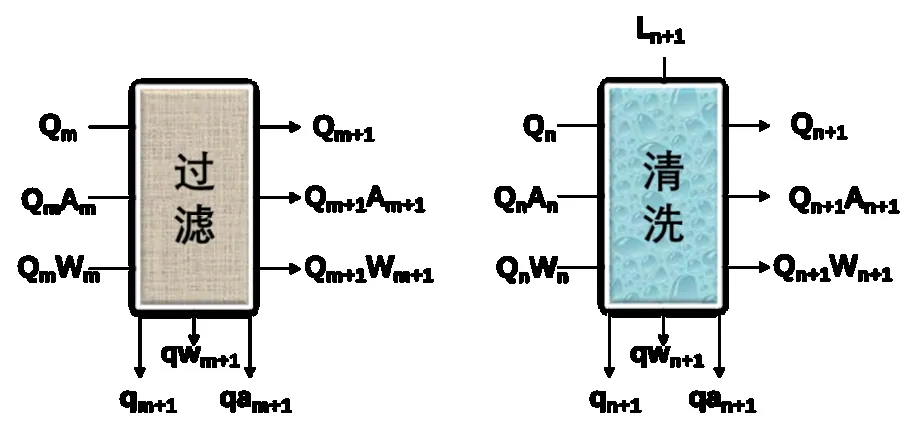
图2 旋叶式动态过滤机过滤、清洗模型

2 过滤模型及模拟

在单一过滤条件下，对+1 级的液体进行衡算。

浆料质量流速平衡

浆料内含固量平衡

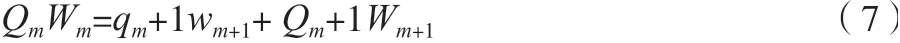
式中：W为+1 级滤板进料端浆料的固含量；W为+1级滤板出料端浆料的固含量；w为+1 级滤板过滤端浆料的固含量。

在旋叶式动态过滤机中，流体平行流过过滤介质表面，由此产生的剪应力使过滤介质表面上的滤饼减薄，进而影响过滤速度。桨叶的转速影响流体的切向速度，而切向速度的大小又直接影响剪应力值，对过滤速率有重要影响，由此可对其进行假设，如公式（8）所示。

式中：为过滤面上任一一点处的过滤速度；为过滤面上任意一点半径；为滤室压力；u为流体的切向速度；、、、为试验常数，分别与设备参数、过滤速率、腔体压力及滤板直径有关。

将上式积分代入得：

将、u代入上式得：

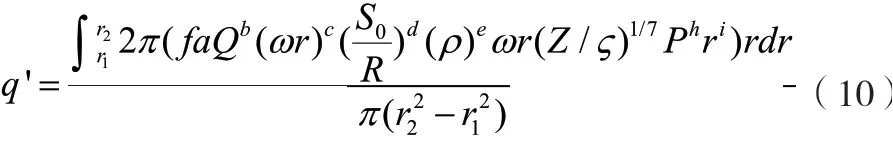
计算得：

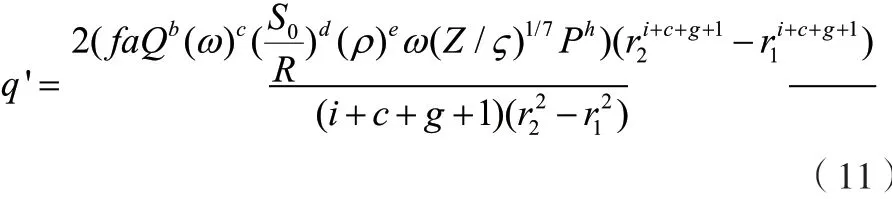
各膜室尺寸相同，假设物料密度相同，各试验常数简化得公式（12）。

将8 级浓缩看成一级浓缩，在同一条件不同进料流量下进行拟合，结果如图3（a）所示，测得常数b=0.363；同理在同一条件不同转速（图3（b））、同一条件不同压力下（图3（c））对流量进行拟合，分别测得=-0.103，=-0.167，再经过逐级拟合得到=0.15，即得到每级滤液流量如公式（13）所示。

为验证其准确性，将不同试验条件下的数据代入上式，将实际流量与拟合流量对比，如图3（d）所示，可知该式在一定误差内可用于推测实际试验过程。

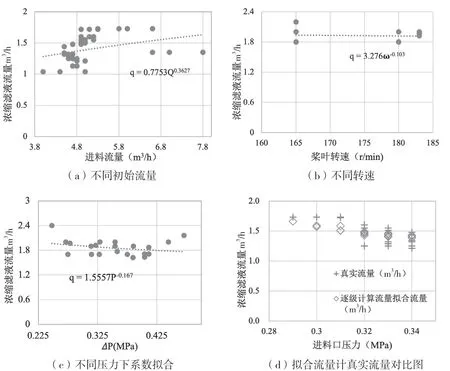
图3 过滤阶段

3 清洗模型及模拟

在清洗过程中，研究对象主要是浆料中的钠离子含量，滤液流量和固含量拟合借鉴过滤过程影响，因此对钠离子可作以下平衡模型。

3.1 浆料质量流速平衡

3.2 溶液中钠离子量平衡

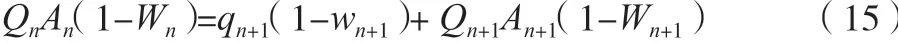
在清洗过程中，假设其可以完全混合，则会有+1=+1，实际过程中不存在，可以做如下假设。

式中：、—钠离子含量（mg/L）；—清洗阶段滤板级数；—混合系数。

对清洗过程来说0＜＜1，将公式（14）代入公式（15），进行简化及合并可得。

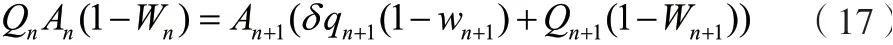
在动态过滤机频率39Hz，转速为183r/min 条件下，考察浆料进料流量对单级洗涤滤液流量的影响，试验结果如图4（a）所示。在浆料进料流量在2 m³/h～4 m³/h 内，浆料进料流量对洗涤滤液流量影响不大，略有下降趋势。对试验数据进行乘幂模拟，可得模型参数=-0.256。

操作压力对洗涤段单级滤液流量的影响如图4（b）所示。随着操作压力逐渐增大，过滤滤液流量呈先降低后稍增趋势，进一步说明在压力不断增大的情况下，滤膜逐渐致密，流量增大。在此条件下对其进行乘幂模拟，可得模型参数=0.5567；同理，不同转速对洗涤阶段单级清洗滤液流量的影响如图4（c）所示，可得模型参数=-0.185。

通过以上试验数据模拟得到的各工艺条件的模型参数，再对所有数据进行逐级拟合得到模型参数=0.65，即得到洗涤段每级滤液流量，如公式（18）

为验证其准确性，将不同试验条件下的数据代入上式，将单级洗涤滤液试验流量与计算流量对比作图，如图4（d）所示，计算结果与试验结果比较吻合，该模型可用于实际过程的模拟计算。

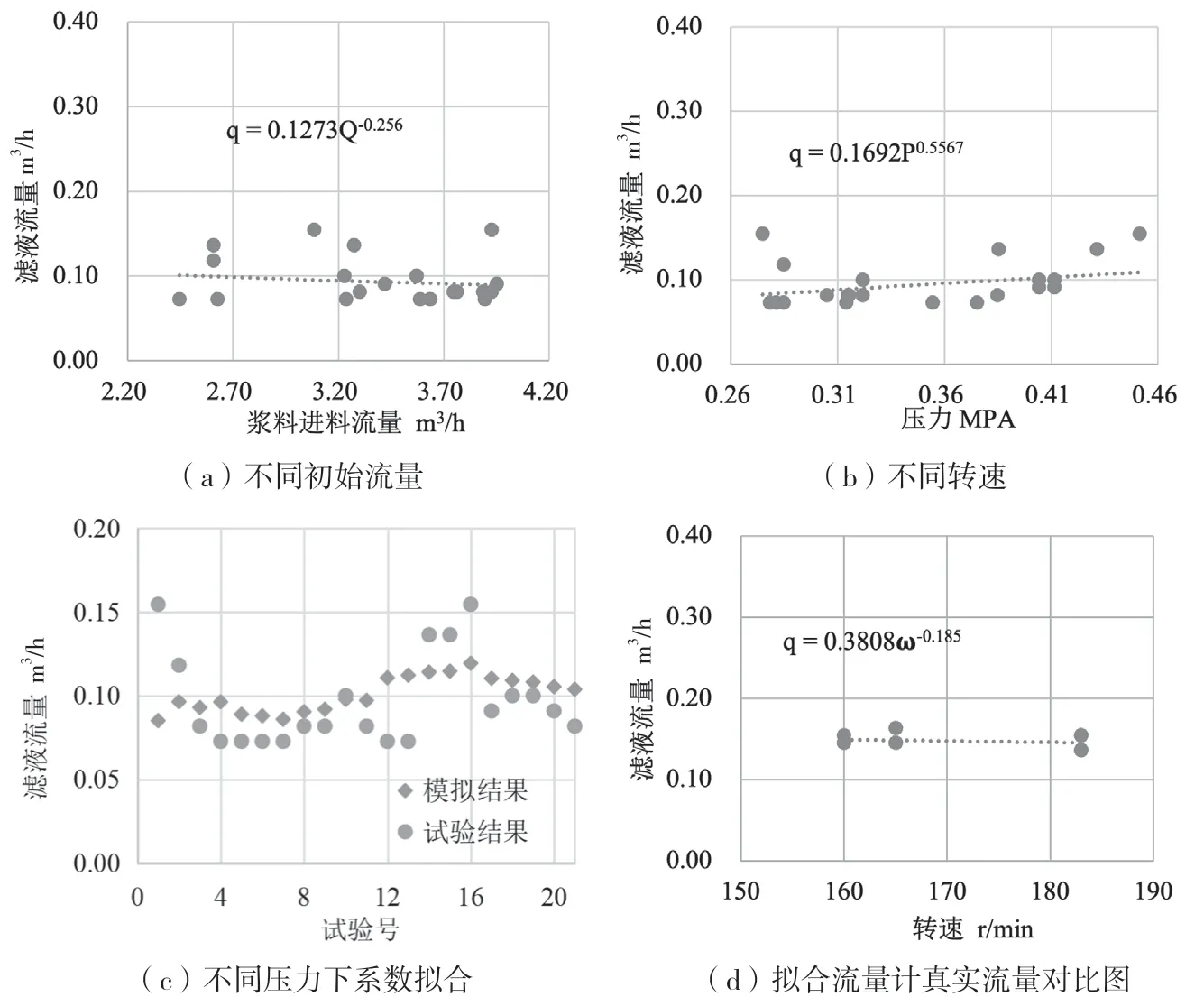
图4 过滤阶段

在不同试验条件下，设备运行一段时间，各流量数据基本稳定后，分别取过滤段滤液、洗涤段滤液、出料滤渣分析各样品的Na+含量和固体含量。试验条件以及分析结果见表1。

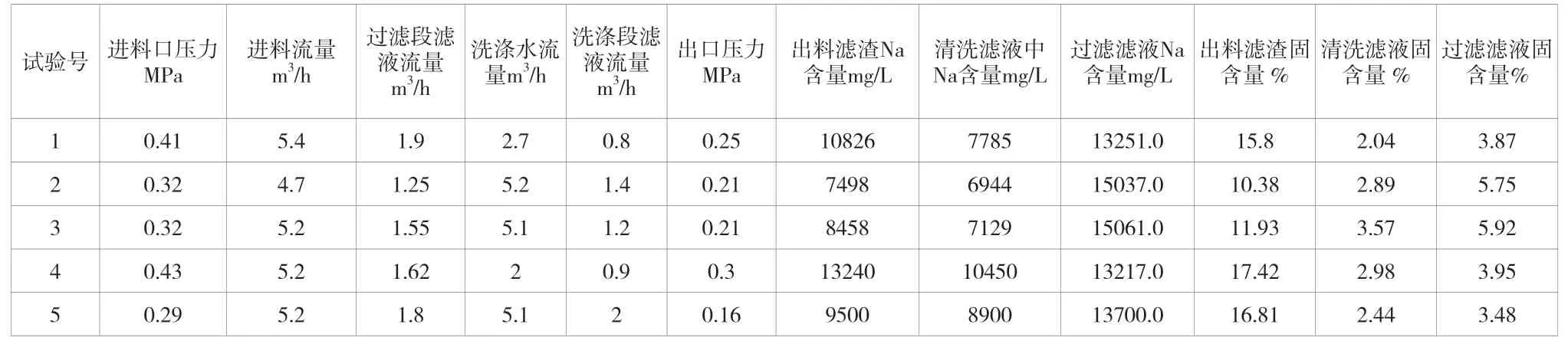
表1 不同试验条件及分析数据

根据Na+平衡模型，以及清洗段滤液模型，对洗涤段各级Na+含量进行模拟计算，对不同条件试验数据进行优化，得到混合系数=0.585，模拟情况见图5。从表中数据可见模拟结果与实际结果有较好的稳合性，相对误差小于6%。

图5 不同试验条件洗涤段Na+模拟计算结果对比图

进而，为进一步揭示旋叶式动态过滤机的清洗效果，定义两个指标：洗涤效率（）和Na总脱除率（）。

洗涤效率（）=洗涤滤液中Na质量流量/洗涤水总进料流量

总脱除率（）=（进料中的Na量-出料滤渣中的Na量）/进料中的Na量

根据不同试验条件下得到的旋叶式动态过滤机试验数据，根据物料平衡和分析结果进行洗涤性能的计算，计算结果见表2。从表中可见，不同工艺条件下，洗涤效率差异比较大，总体来看，洗涤水流量降低，洗涤效率提高，但Na脱出率太低。在同一设备条件下，进料流量与洗涤水进水流量的比例是决定清洗效果的关键因素。

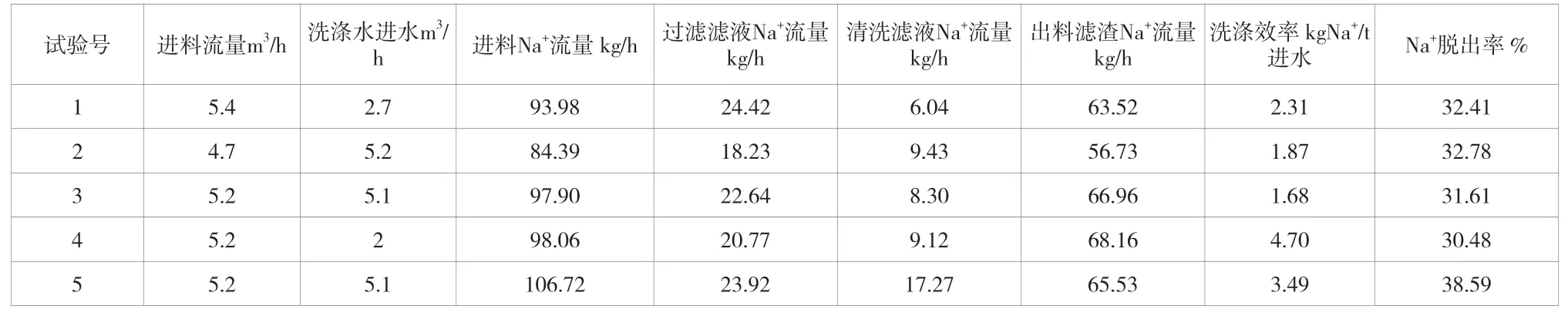
表2 不同试验条件洗涤性能分析结果

4 结语

该文在充分分析动态过滤机运行机理和流体流动状态基础上，利用丝光沸石分子筛浆料建立了旋叶式动态过滤机过滤、清洗模型。该文从指导动态过滤机在物料清洗过程中的实际应用出发，假设了丝光沸石分子筛过滤清洗混合系数，可以很好地预测清洗水的加入量，达到进一步提高清洗效率的目的。在此基础上，利用不同的过滤数据和清洗数据进行了模型计算，计算结果与实际结果相符。结果表明，通过过滤模型的建立，实际生产与拟合数据误差不超过6%，在导动态过滤机清洗和条件选择方面有一定的指导意义。然而，因物料性质不同在相同装置上的滤液通量也不相同，须进一步进行试验得出适应不同过滤介质的模型。