对流换热数值模拟

李 皓

（中国直升机设计研究所，江西 景德镇 333000）

0 引言

随着计算机性能的飞速发展以及计算流体力学（Computational Fuild Dynamics，CFD）技术的不断进步，数值模拟方法获得了蓬勃发展。鉴于其经济快捷的特性，在设计初期使用数值模拟来指导设计过程能大大降低设计成本，减少设计周期。在飞机防除冰系统的设计过程中，首先需要通过数值模拟来确定防护范围、防冰所需热流等，进而才能开始整个防除冰系统的初步设计[1]。

由于飞机飞行速度快，对流换热是热量传递过程中的主要热流项，对结冰过程、加热除冰过程有至关重要的影响。能否获得准确的对流换热系数会直接关系到防除冰系统设计的准确性，因此进行对流换热系数计算准确性的研究是非常必要的[2]。

该文的数值计算工作基于FLUENT 软件。作为如今CFD 领域最全面的软件之一，FLUENT 提供了多种求解方法和湍流模型，包括Spalart-Allmaras（S-A）湍流模型和Transition SST 湍流模型等，具有较高的求解精度。该文通过计算不同底层网格厚度、不同疏密网格、不同参考温度、不同换热温差下的对流换热系数，分析参数变化对计算结果的影响，确定了更精确的计算方法。最后将采用S-A 湍流模型和Transition SST 湍流模型的计算结果与国外文献中的试验数据进行对比，验证了该数值计算结果的准确性，可为数值仿真工作人员提供一定参考。

1 对流换热系数的计算

通过牛顿冷却公式可以得到对流换热系数h，如公式（1）所示。

式中：q为壁面总热流；Tw为壁面温度；Tref为参考温度。

根据公式（1）可知，选取不同的参考温度会获得不同的对流换热系数。为尽可能获得准确值，应该选取更加贴近实际的计算方法。因此该文分别选取来流静温T∞、来流总温Tt和绝热壁温Tad作为参考温度，来计算对流换热系数，如公式（2）～公式（4）所示。

式中：r为恢复系数，其值为1.4；Ma为马赫数。

2 网格无关性验证

采用FLUENT软件计算对流换热系数实质上是计算空气流场，并求解Navier-Stokes 方程。空气流场的数值计算受到计算域的空间离散条件的影响，在贴近壁面附近需要足够细密的网格来解析黏性底层。为了获得网格无关解，需要进行网格无关性验证。

首先，该文选择半圆型的试验件作为仿真模型，试验件半圆直径为44.5 mm，并在后面连接一个锥状的后体以保持连续的气动外形，易于计算收敛。其次，利用Gridgen 软件来划分结构网格，如图1 所示。计算域尺寸约为7 m，只有范围足够大，才能保证远场边界条件成立，不会影响到壁面附近的空气流场。并选取0.001 mm、0.005 mm、0.01 mm、0.05 mm 和0.1 mm 共5 种不同的底层网格厚度进行计算，不同网格的无量纲壁面距离y+在0.1～45.0。

图1 Gridgen 划分C 字型结构网格

再次，选用Spalart-Allmaras 湍流模型计算空气流场。空气采用理想气体，比热cp=1 006.43 J/（kg·K），空气导热系数λ=0.023 56 W/（m·K），动力黏性系数μ=1.789 4×10-5kg/（m·s）。并设置压力远场和等温壁面，环境压力P=34 500 Pa，马赫数Ma=0.25，壁面温度Tw=273.15 K，环境温度Tinf=253.15 K。最后，通过壁面总热流来分析网格无关性，通过计算得到的壁面总热流如图2 所示。

根据图2 可知，基于不同底层网格厚度计算出来的壁面总热流存在较大的差异，可见底层网格厚度能显著影响计算结果。而随着底层网格厚度减少，计算结果也逐渐趋于稳定，厚度为0.001 mm 和0.005 mm 网格的计算结果几乎完全重合。由于0.005 mm 厚度的网格的y+≈1，因此可以认为0.005 mm 厚度的网格已经足够细密，计算结果即表现出网格无关性。

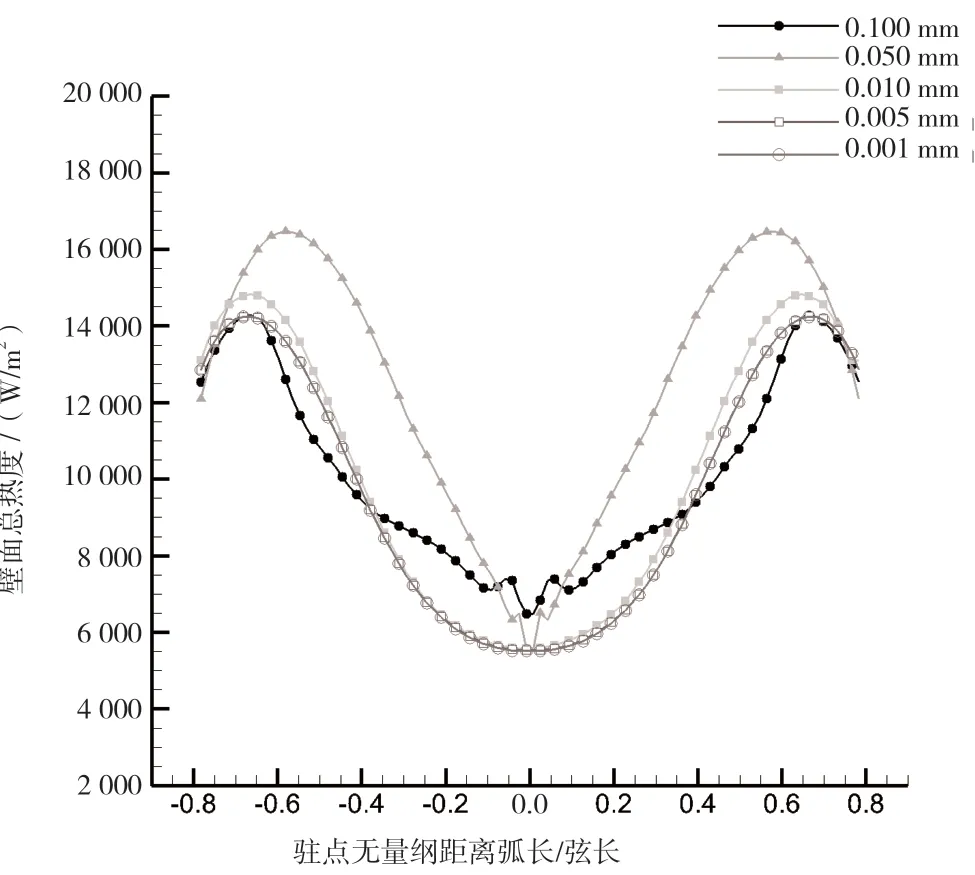
图2 不同底层网格厚度下的壁面总热流

除了底层网格厚度对计算结果有较大影响之外，网格的疏密也会影响计算的准确性。因此为了获得网格无关解，还需要验证网格疏密对计算结果的影响。该文选取3套不同疏密的网格，底层网格厚度均为0.005 mm，网格数量分别为70 850 个、58 000 个和30 240 个。计算得到的壁面总热流结果如图3 所示。

根据图3 可知，基于3 套不同疏密的网格计算得到的壁面总热流在总体趋势和范围上差距不大，但细节上存在较大的不同。粗糙网格的网格数量少，划分不够精细，热流曲线呈折线状，过渡不够平滑。精细网格的网格数量较多，反而出现了锯齿形的波动，可能是由网格划分的质量引起的。可见中等数量网格的计算结果的连续性最好。

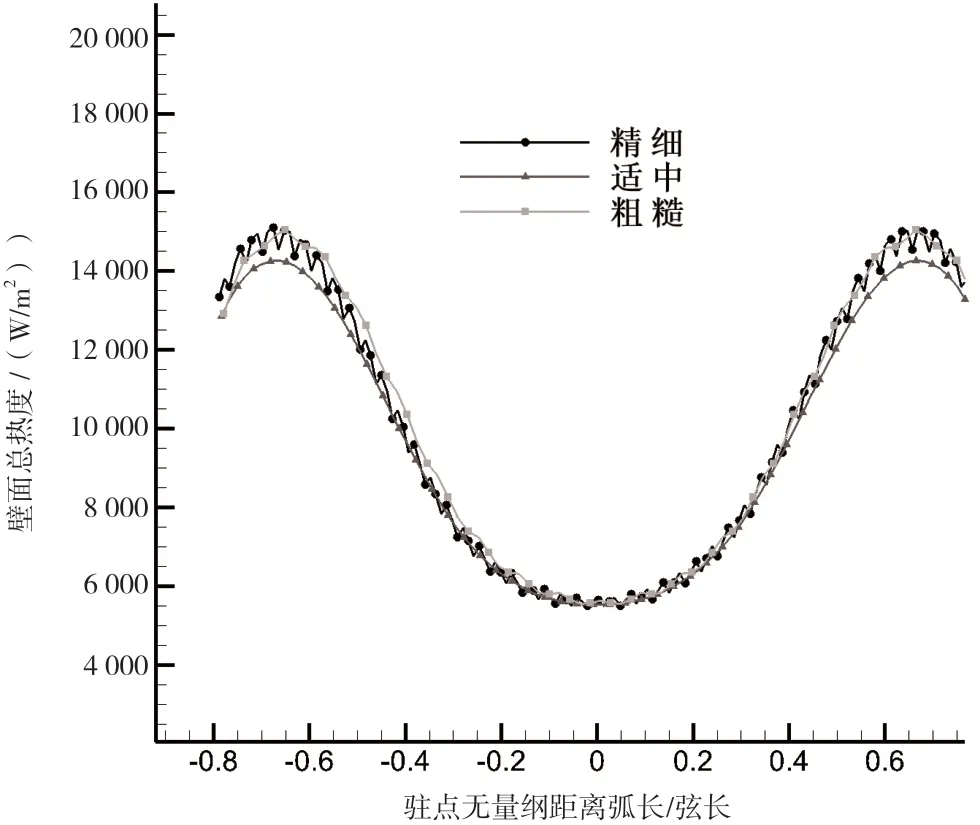
图3 不同疏密网格下的壁面总热流

3 参考温度对对流换热系数的影响

该文选择来流静温作为参考温度来计算对流换热系数h，计算条件模型和网格同第2 节，底层网格厚度0.005 mm，网格数量适中。采用Transition SST 湍流模型，空气采用理想气体，并设置压力远场和等温壁面，环境压力P=34 500 Pa，马赫数Ma=0.25，攻角为0°，环境温度T∞=253.15 K。只改变壁面温度，分别取Tw为263.15 K、273.15 K、283.15 K、293.15 K、303.15 K 和313.15 K。计算结果如图4 所示。

根据图4 可知，基于不同温差（Tw-Tinf）计算得到的对流换热系数相差极大，即随着壁面温度的升高，驻点附近的对流换热系数逐渐增大，而远离驻点的下游处对流换热系数逐渐减小。并且随着温差的增大，计算结果的相对误差逐渐减小。产生该结果的原因主要在于未考虑气动加热的影响，由于驻点附近的空气速度显著降低，动能转化为热能，导致温度有所升高，因此实际的换热温差小于计算值。

显然，简单地将来流静温作为参考温度来计算对流换热系数会存在较大误差，为了消除气动加热的影响，考虑将来流总温作为参考温度，在相同条件下计算得到的对流换热系数曲线如图5 所示。

根据图5 可知，将来流总温作为参考温度进行计算后，消除了驻点附近的计算误差，基于不同壁面温度计算得到的驻点附近的对流换热系数完全相同。因为在驻点附近空气速度接近于0 m/s，可以认为实际温度就是来流总温。而在远离驻点的下游位置，将来流总温作为参考温度进行计算则不够准确。根据图5 也可知，远离驻点位置在换热温差较小时存在较大相对误差。总结图4 和图5 的方法可知，采用来流静温作为壁面温度会导致驻点附近的温度与实际不符，而采用来流总温作为壁面温度则会导致远离驻点区域的温度与实际不符。也即这2 种计算方法都存在一定不足，均会引入较大的相对误差，因此采用等温壁面进行计算是不合适的。

图4 不同换热温差下对流换热系数计算结果（Transition SST 模型，压力远场和等温壁面边界条件）

为了减少误差，如果采用绝热壁面计算出在空气流场作用下壁面的实际温度，并认为在壁面附近的空气温度与壁面温度相同，再将该温度作为参考温度来计算壁面的对流换热系数，就可以消除气动加热引起的误差，改善结果的准确性。计算结果如图6 所示。

根据图6 可知，与图4、图5 的2 种方法相比，图6 的计算结果有极大改善。驻点附近计算结果完全相同，远离驻点的下游区域的相对误差也显著减小。因此采用该种方法作为对流换热系数的简化算法，无须空气流场的反复迭代，误差又能控制在可接受范围内。其对流换热系数h的计算如公式（5）所示。

图5 不同换热温差下对流换热系数计算结果（Transition SST 模型，压力远场和等温壁面边界条件，考虑滞止温升）

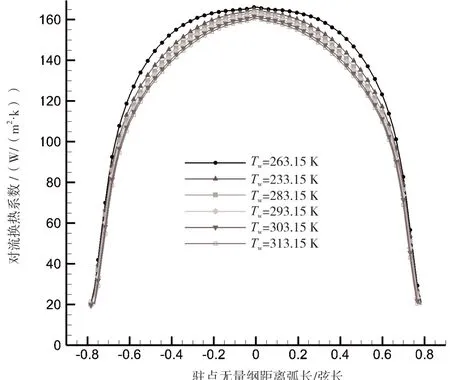
图6 不同换热温差下对流换热系数计算结果（Transition SST 模型，压力远场和绝热壁面边界条件）

驻点无量纲距离弧长/弦长

式中：q为壁面总热流；Tad为绝热条件下的壁面温度。

4 算例验证

为了验证该文对流换热系数计算的准确性，该文选取了美国国家航空航天局（NASA）在Lewis 冰风洞中对NACA0012翼型所做的对流换热试验作为对比。该翼型弦长为0.533 m，取其中2 个算例作为验证，见表1。计算同时采用了S-A 湍流模型和Transition SST 湍流模型，并采用远场边界条件，调节马赫数使自由流速度与试验数据吻合，空气采用理想气体，密度为1.326 kg/m3，动力黏度为1.676 7×10-5kg/（m·s），比热为1 006.43 J/（kg·K），空气导热系数为0.023 56 W/（m·K），环境温度为266.45 K。为了减少相对误差，尽可能增大换热温差，取壁面温度比环境温度高60 ℃。计算所用网格满足第2 节网格无关性验证中的条件y+＜1，第一层网格厚度为0.005 mm。

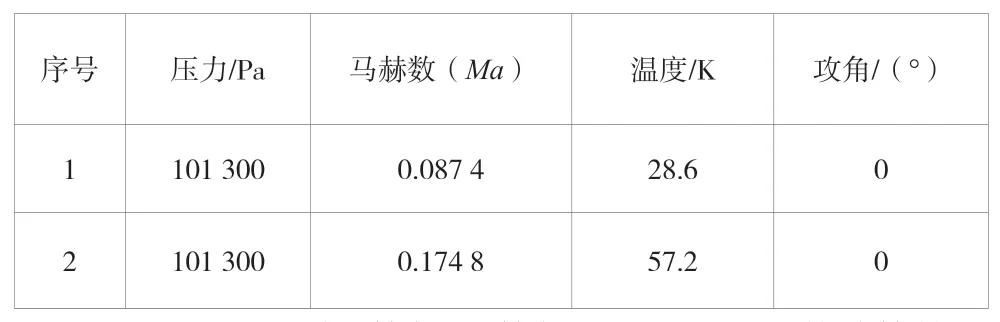
表1 对流换热系数计算条件

图7、图8 分别为算例1、算例2 对流换热系数计算结果与文献试验结果的比较。根据图7、图8 可知，不同的湍流模型计算结果存在较大差异。在驻点附近，S-A 湍流模型和Transition SST 湍流模型的计算结果基本相同，同时也与文献试验结果基本吻合，很好地描述了实际的换热情况。但随着位置往后移动，S-A 模型的转捩很快出现，对流换热系数不再下降，反而有微小回升，比文献试验结果偏高。而Transition SST 模型则在整个试验测量范围内有良好的仿真效果。因此该文后面对对流换热系数的计算全部采用Transition SST 湍流模型。

图7 算例1 对流换热系数计算结果

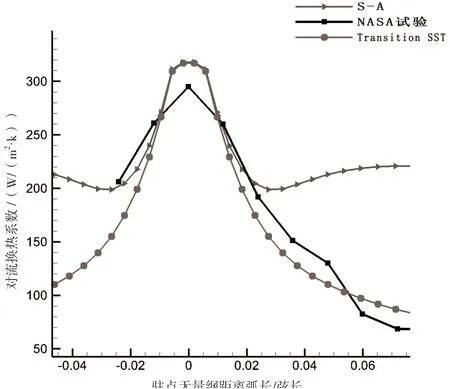
图8 算例2 对流换热系数计算结果

5 结论

该文采用FLUENT 软件计算对流换热系数，根据上述分析和比较可知，网格疏密、第一层网格的厚度、参考温度、换热温差和湍流模型都会对对流换热系数的计算结果产生影响。要想得到尽可能准确的计算结果，应遵循以下规律：1） 保证较好的网格质量。过于密集的网格可能造成网格质量的下降，过于稀疏的网格则会引入较大的计算误差。2） 底层网格厚度对对流换热系数计算准确性影响很大，应尽可能保证网格的无量纲壁面距离y+接近或小于1。3） 在仿真时尽可能增大换热温差，以缩小相对误差。4） 选择不同的参考温度会影响对流换热系数计算结果。应采用绝热壁面计算气动加热作用下的壁面温度，用该温度作为参考温度来计算对流换热系数，这样能消除由于气动加热引起的误差。5） 不同湍流模型对计算结果也有影响。在该文的算例下，Transition SST 模型的计算结果表现出了更好的符合性。