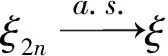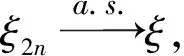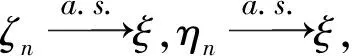不确定序列几乎必然收敛的几个性质
2022-07-02孙秀花
孙秀花
(晋中学院 数学系,山西 晋中 030600)
不确定测度[1-4]、不确定变量[5]、不确定分布[6]是不确定理论中三个基本的概念,收敛性是不确定变量序列(简称不确定序列)的性质之一,几乎必然收敛是Liu[1]2007年提出的,本文主要研究了不确定序列几乎必然收敛的几个性质,这些性质对不确定序列的几乎一致必然收敛[7-8]、依测度收敛[9]及依度量收敛[10]的性质研究具有一定的意义.
1 预备知识
定义1.1[1]设Γ为一个非空集合,L是Γ上的σ-代数.L中的每一个元素称为一个事件.如果集函数M:L→R满足:
(ⅰ)(正规性)M(Γ)=1;
(ⅱ)(单调性)若A1⊂A2,则M(A1)≤M(A2);
(ⅲ)(自对偶性)M(A)+M(Ac)=1,∀A∈L;
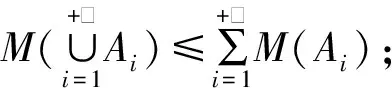
则称M为不确定测度,(Γ,L,M)为不确定测度空间.
定理1.1[1]对于任意的事件Λ,有M()=0和0≤M(Λ)≤1.
定理1.2[10]假设事件Λ1,Λ2,满足M(Λi)=1,i=1,2那么M(Λ1∩Λ2)=1.
定义1.2[1]从不确定测度空间(Γ,L,M)到实数集的实值可测函数称为不确定变量.
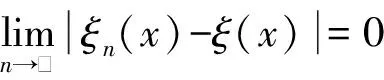
定义1.4设ξ,η是定义在不确定测度空间(Γ,L,M)上的不确定变量,
(ⅰ)称ξ与η几乎处处相等,如果M{x∈Γ|ξ(x)≠η(x)}=0,记作ξ~η或ξ=η,a.e.;
(ⅱ)称ξ(x)小于等于η(x),如果对∀x∈Γ,有ξ(x)≤η(x),记作ξ≤η.
定理1.3[1]设ξ1,ξ2,…,ξn是不确定变量,函数f:n→是可测的实值函数,则ξ=f(ξ1,ξ2,…,ξn)是不确定变量.
2 不确定序列几乎必然收敛的性质
以下定理中的{ξn},{ηn}是不确定测度空间(Γ,L,M)上的不确定序列,ξ,η是(Γ,L,M)上的不确定变量.
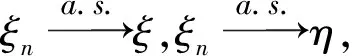
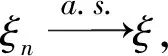
ξn(x)→ξ(x)(n→∞),
(1)
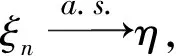
ξn(x)→η(x)(n→∞),
(2)
令C=A∩B,则由定理1.2得M(C)=1,在C上,式(1)和式(2)同时成立,根据极限的唯一性得,
ξ(x)=η(x),∀x∈C.
所以
{ξ(x)≠η(x)}⊂Cc,
根据不确定测度的单调性和自对偶性有
M{ξ(x)≠η(x)}≤M(Cc)=1-M(C)=0
再由测度的非负性知M{ξ(x)≠η(x)}=0,即ξ=η,a.e.
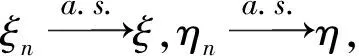
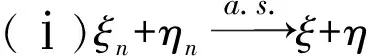
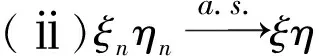
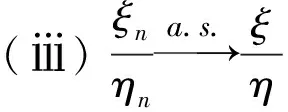
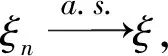
ξn(x)→ξ(x)(n→∞),
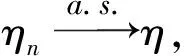
ηn(x)→η(x)(n→∞),
令C=A∩B,则M(C)=1,则在C上有,
ξn(x)+ηn(x)→ξ(x)+η(x)(n→∞)
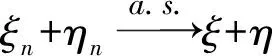
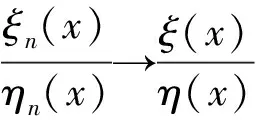
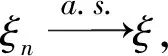
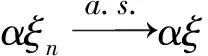

证明 当α=0时,显然成立;
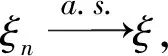
结合定理2.2和定理2.3可得下面推论:
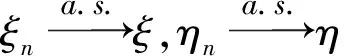
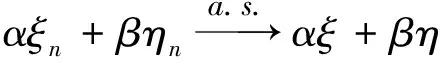
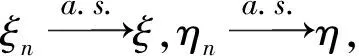
证明 应用公式
由定理2.3和推论2.1易知结论成立.
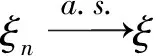
证明 因为f(x)为上的连续函数,所以f(x)为可测函数,又ξn和ξ为不确定变量,由定理1.3 知对任意的ξn和ξ,f(ξn)和f(ξ)也为不确定变量.若(n→∞),则存在集合A且M(A)=1,在A上,ξn(x)→ξ(x)(n→∞),又f(x)为上的连续函数,知f(x)在A上也连续,所以f(ξn(x))→f(ξ(x))(n→∞),即(n→∞).
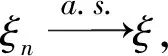
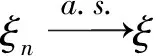
M{ξ(x)<0}≤M(Ac)=1-M(A)=0
再由不确定测度的非负性,知M{ξ(x)<0}=0.即ξ≥0,a.e.
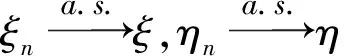
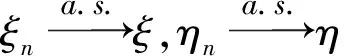
3 不确定序列几乎必然收敛的判定方法
定理3.1设ξ,ξ1,ξ2,…,ξn是定义在不确定测度空间(Γ,L,M)上的不确定变量,则
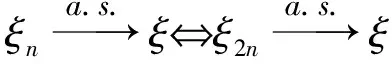
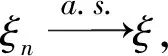
所以在A上也有
ξ2n(x)→ξ(x),ξ2n+1(x)→ξ(x)(n→∞),