基于分块矩阵法优化测量矩阵的研究
2022-07-02宋儒瑛张朝阳
宋儒瑛,张朝阳
(太原师范学院 数学系,山西 晋中 030600)
0 引言
如果存在一个常数δk∈(0,1),使得下式成立,则称矩阵A满足k阶的限制等距性(RIP)(restricted isometry property):
其中x∈∑k={x:‖x‖0≤k}.
RIP是测量矩阵应该满足的充分条件而非必要条件,并且直接判断一个矩阵是否满足限制等距性是非常困难的.Baraniuk指出:稀疏变换矩阵与测量矩阵不相关是RIP的等价条件,也就是说稀疏变换矩阵与测量矩阵之间的相关性很小时,感知矩阵(测量矩阵与稀疏变换矩阵的乘积)能够满足RIP的概率会很高.相关性因为计算量小、物理意义明确,所以在测量矩阵的优化中被广泛用来衡量测量矩阵性能的指标.
虽然文献[1-4]所涉及的框架理论降低了测量矩阵的相关性,但是计算复杂度还是比较高的,因此本文在分块矩阵的思想下直接构造了一个新的测量矩阵,而且分别从理论和实验两个方面证明了所构造矩阵的可行性.文献[5-7]介绍了常见的恢复算法和矩阵的构造方法,文献[7-14]介绍了压缩感知的基础知识及其应用,这里不做详细介绍.
1 预备知识
矩阵A的相关性是指A的任意两列ai、aj之间最大的绝对内积,数学表达式如下:
矩阵A的l1-相关性函数的数学表达式如下:
其中A∈Cm×N,并且矩阵A的列是l2范数单位化列,即‖ai‖2=1,i∈[N].
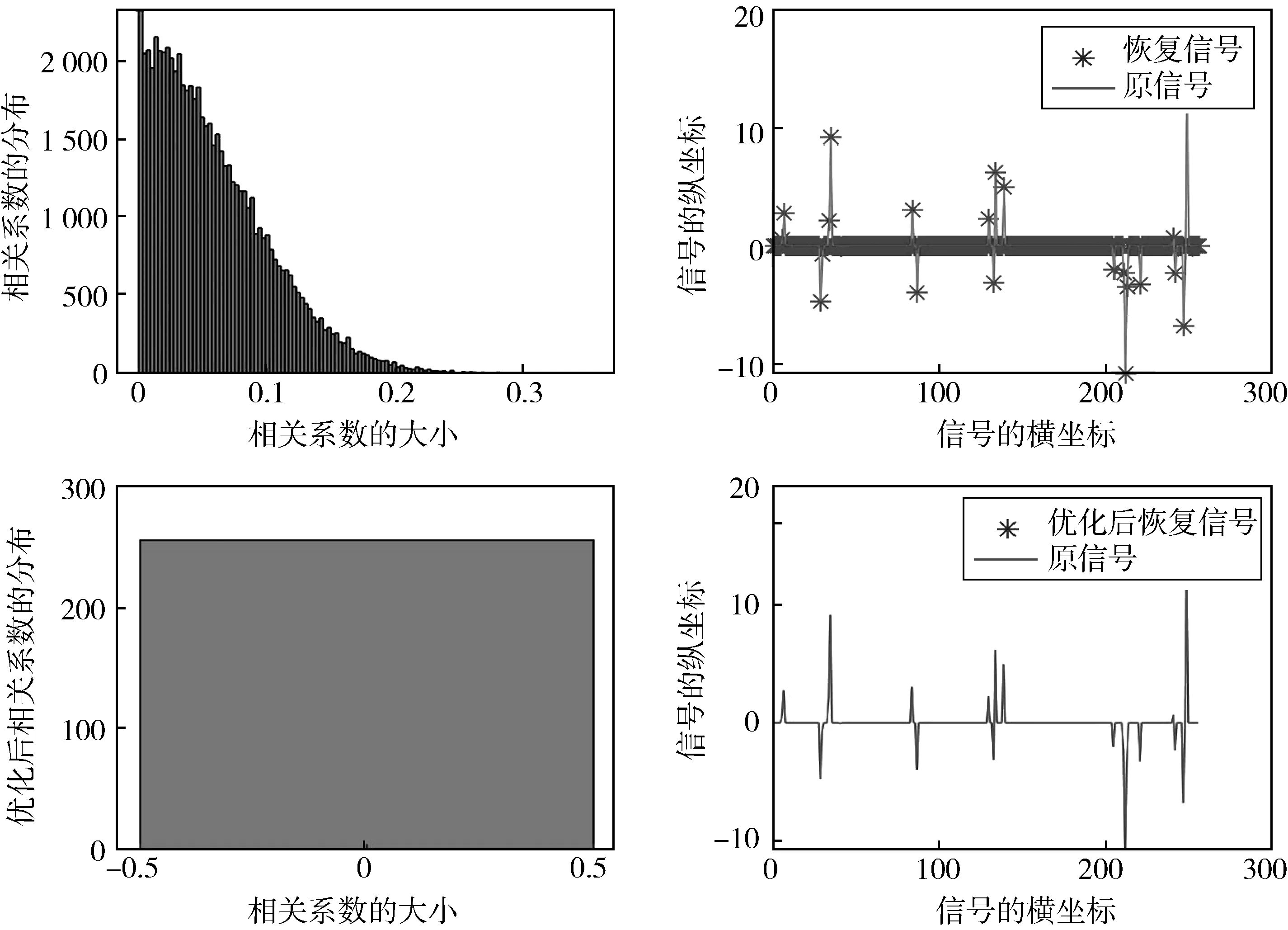
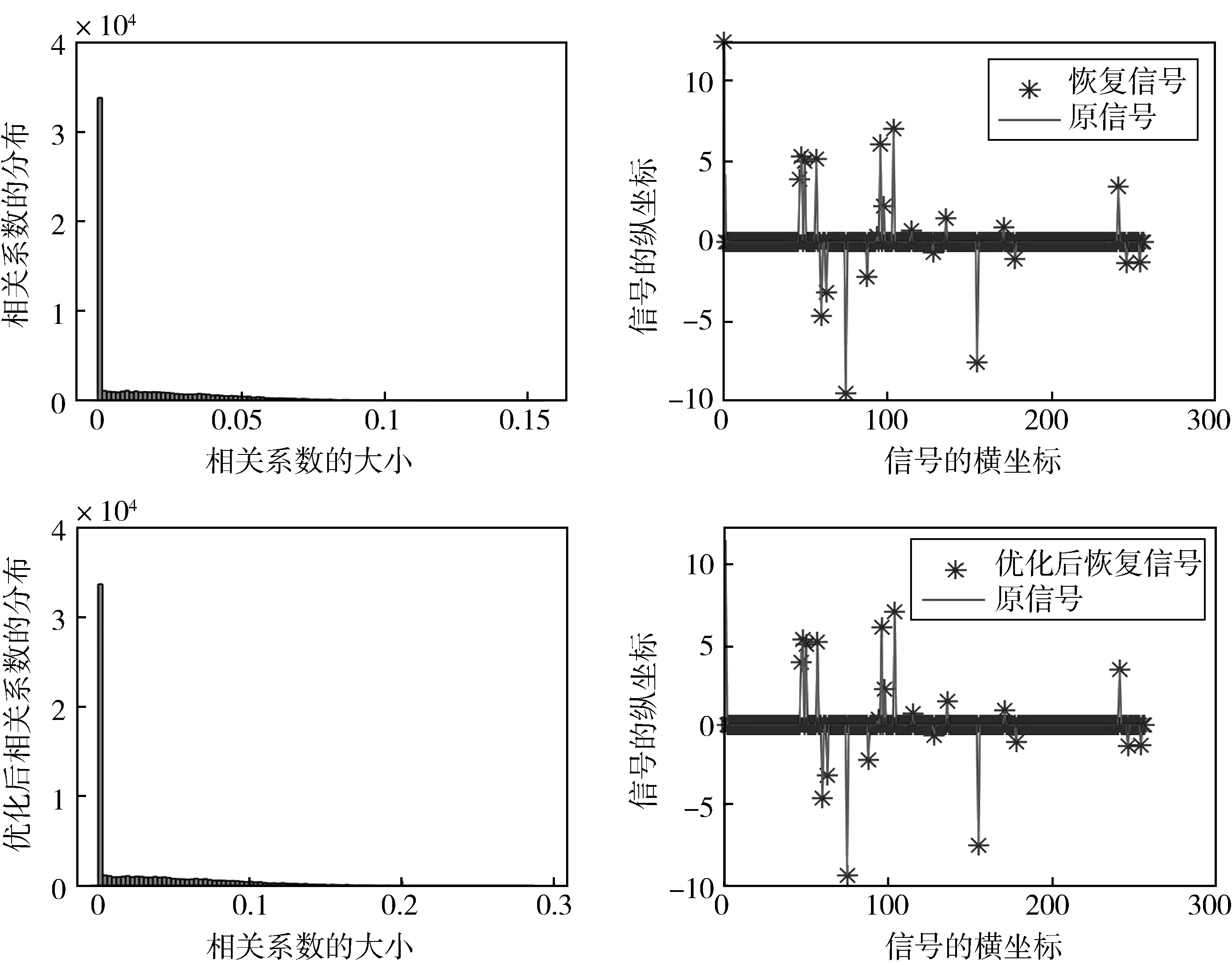
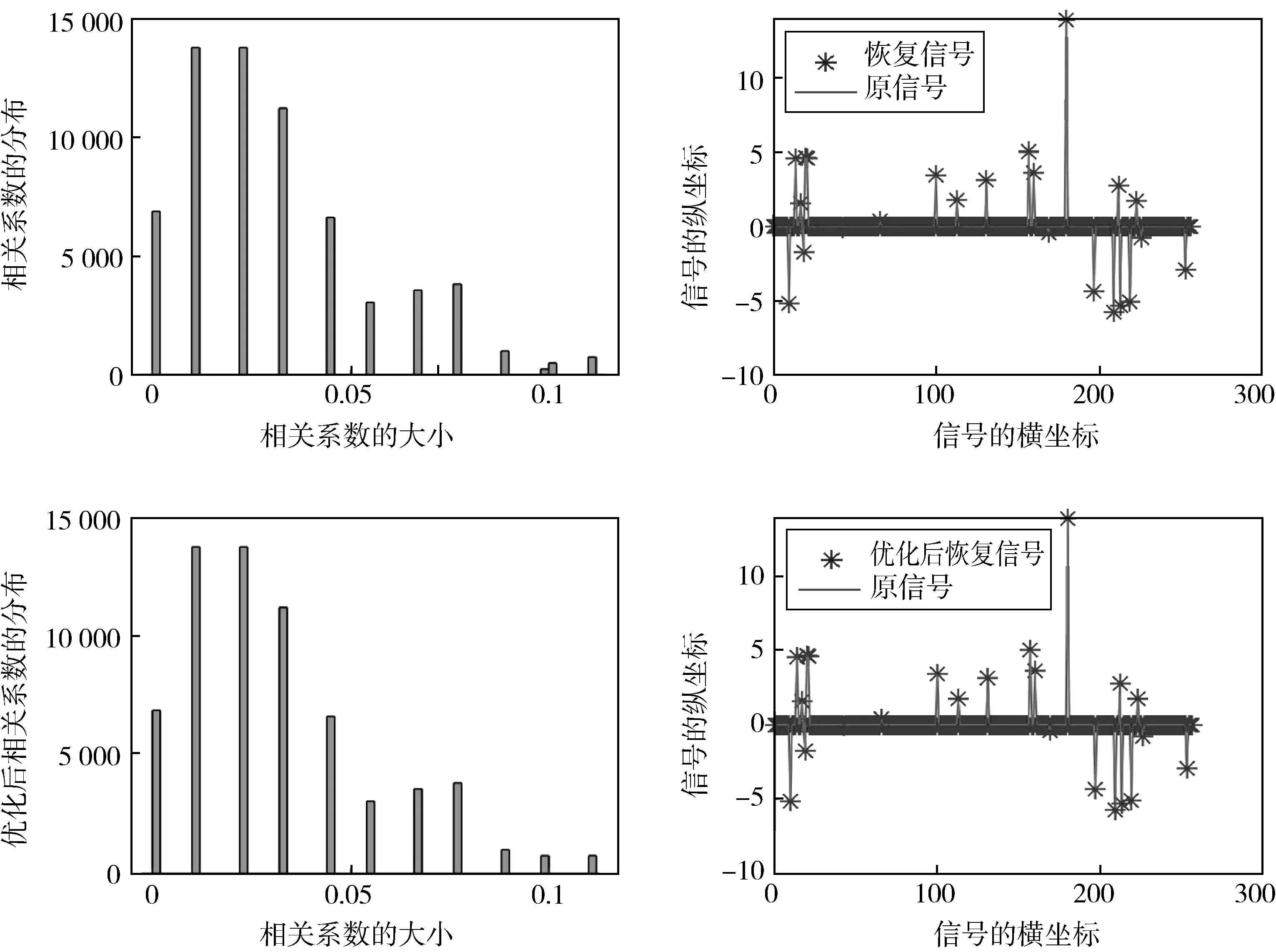
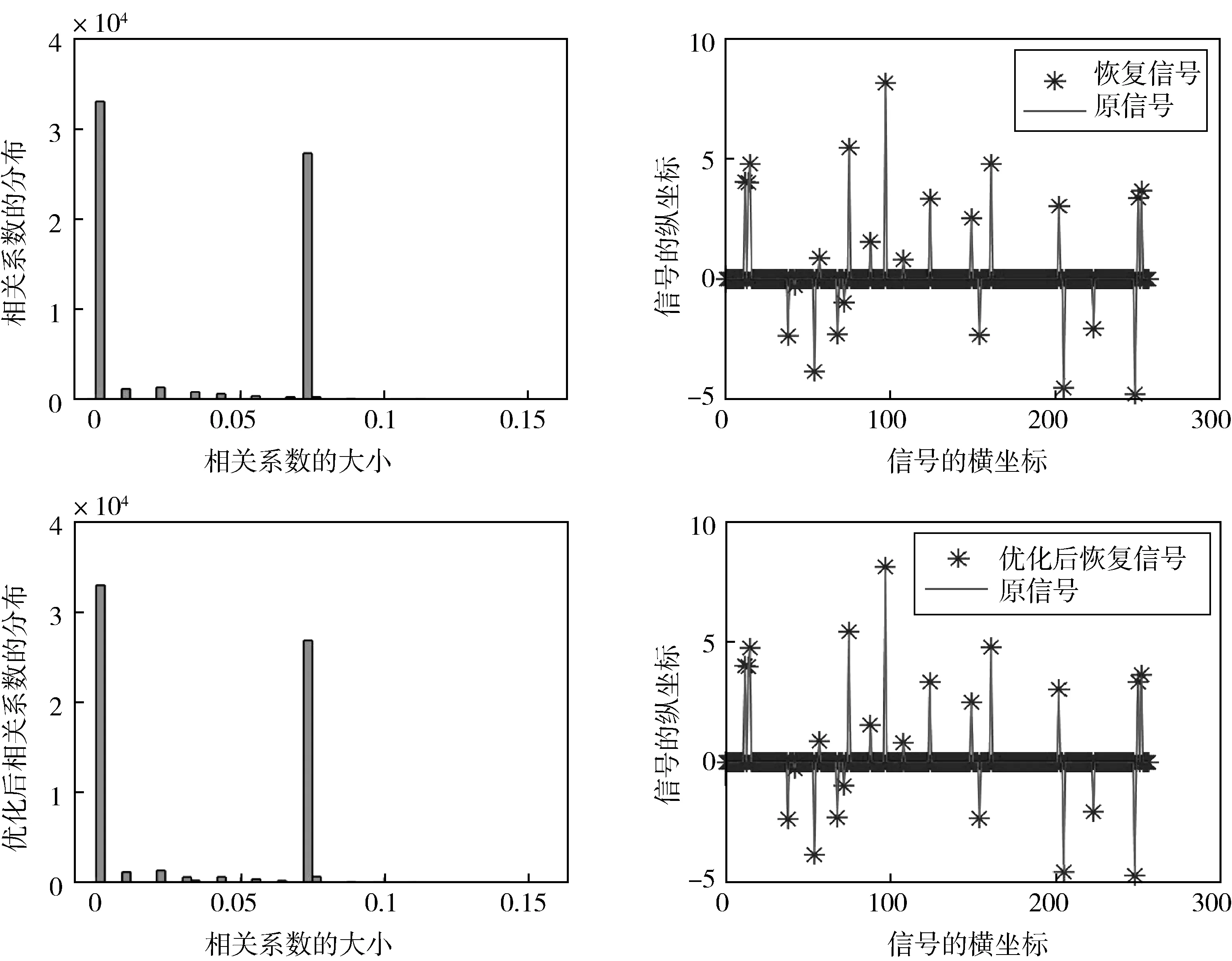
梯度下降算法:假设信号x∈Rn在n×n维的稀疏变换矩阵Ψ下的投影是稀疏的,通过m×n维的测量矩阵Φ可以得到m(m< 梯度下降算法的思想在于让Gram矩阵G逼近单位矩阵I,即 梯度下降算法是对初始测量矩阵进行优化,使得优化后矩阵的相关性得到降低,这样的过程难免有些复杂.自然地问是否存在这样的一个新的优化测量矩阵,使得优化前后它的相关性没有太大的变化,而且它本身的相关性就比较低? 基于上述所提问题,本文用分块矩阵法构造了一个新的测量矩阵,即A=[Im×m,C],其中Im×m是单位矩阵,C可以选择常见的初始化测量矩阵,如Gaussian矩阵和部分Hadamard矩阵.利用梯度下降算法,对测量矩阵A进行优化,通过下面数值实验:分析、比较优化前后相关性的变化情况以及实验误差,说明我们构造的测量矩阵是可行的,所提的问题是合理的. 实验表明,当A=[Im×m,C],C为部分Hadamard矩阵时,构造效果最佳,优化前后它的相关性没有太大的变化,而且它本身的相关性就比较低. 正交匹配追踪算法的思想是迭代优化算法的核心,其思想中涉及的正则化操作是正交投影的具体体现,因此对正交匹配追踪(Orthogonal Matching Pursuit)进行收敛性分析就显得尤为重要.目前针对OMP算法的收敛性分析大多是基于RIP进行的,本人基于相关性函数对OMP算法的收敛性进行了证明,最后也通过数值实验说明了所提出定理的有效性. 表1 正交匹配追踪(Orthogonal Matching Pursuit) 为了建立收敛性定理,我们先建立如下的四个引理: 证明 对于在支撑集S∪{j}上具有形如v+tej的向量,其中t∈C,可以得到 令t=ρeiθ,其中ρ≥0,θ∈[0,2π),那么 这是一个关于ρ的二次多项式,当ρ=|A*(y-Av)j|时,等式成立.这也表明 证明:根据v的定义可得,Av是y在空间{Az,supp(z)⊂S}上的垂直投影,因此, 〈A*(y-Av),z〉=〈y-Av,Az〉=0,z∈CN,supp(z)⊂S 证毕. 引理2.3令矩阵Am×N是l2范数单位化矩阵,且令s∈[N].对所有的s稀疏向量x∈CN,有 上式在集合{x∈CN,supp(x)⊂[N],‖x‖2=1}上的最大值刚好是λmax,最小值是λmin,这也很好地解释了引理2.3中的等价性. 引理2.4给定矩阵A∈Cm×N,非零向量x∈CN是在支撑集S上的,y=Ax,要想通过OMP算法在至多s次迭代后恢复信号x,当且仅当矩阵AS是单射矩阵,而且下列不等式恒成立: 其中,非零向量r∈{Az,supp(z)⊂S},card(S)=s,Sc是S相较于[N]的余集. 证明 假设所有在支撑集S上的信号x,通过OMP算法至多需要card(S)=s次迭代便可恢复.设在支撑集S上的两个非零向量x,z,满足Az=Ax=y,那么z=x,这说明AS为单射矩阵.此外,第一次选取的支撑通常在目标支撑集中,如果对于在支撑集S上的x∈CN,有y=Ax成立,那么第一次迭代过程中支撑l∈Sc是不能被选取的,即 |(A*y)j|>|(A*y)l| 为了证明充分性,假设Ax1≠y,…,Axs-1≠y,需要证明:当0≤n≤s时,n维支撑集S的一个子集是Sn,这将表明Ss=S.与此同时,因为AS为单射矩阵,根据(OMP2)求解Axs=y,易得xs=x. 对于0≤n≤s-1,从引理2.2可以得到(A*rn)Sn=0向量.于是根据(OMP1)的定义可知,索引jn+1不包含在支撑集Sn内,这就证明了支撑集Sn是n维的.综合可得,引理2.4得到了证明. 基于以上四个引理,接下来将给出OMP算法的收敛性证明,即定理2.1. 定理2.1令矩阵Am×N是l2范数单位化矩阵,如果μ1(s)+μ1(s-1)<1,那么每个s稀疏向量x∈CN能够通过正交匹配追踪算法在不超过s次迭代后从测量向量y=Ax中恢复. 证明:让a1,a2,…,aN表示A的l2范数单位化列.根据引理2.4,需要证明矩阵AS为单射矩阵,并且对于所有的非零向量r∈{Az,supp(z)⊂S},有下列不等式成立: 另一方面,由于 此时结合定理2.1的条件μ1(s)+μ1(s-1)<1,可以得到 因此只要μ1(s)+μ1(s-1)<1,那么就可以通过OMP算法恢复原始稀疏信号. 实验中我们选择梯度下降的优化方法,目标函数如下: 定义误差函数: 迭代步骤: 当E<ε,迭代过程终止. 选择Gaussian矩阵和部分Hadamard矩阵依次作为初始化测量矩阵A.由于产生的信号是稀疏的,因此稀疏变换矩阵选择单位矩阵I,此时感知矩阵就是测量矩阵.实验中m=180,N=256,稀疏度s=23,步长η=0.01,ε=1×10-3,稀疏变换矩阵Ψ=IN×N,产生的是随机稀疏信号,列向量的最大相关系数代表着相关性的大小.值得指出的是,实验和理论中的测量矩阵都是经过列单位化处理过的. 图1中选择了高斯随机矩阵作为我们的测量矩阵A,实验表明高斯随机矩阵可以作为测量矩阵,而且恢复误差(恢复信号和原信号的差值)可以忽略不计,图1上半部分的恢复误差为1.257 6×10-13,运行时间为0.004 3.由图1可以看到高斯随机矩阵的列向量相关系数还是比较大的,因此对其进行了优化,图1的下半部分是优化后得到的图像.通过图像可以看到此时的恢复误差太大,运行时间为0.032 3,所以直接对高斯随机矩阵进行优化的思路是行不通的.在分块矩阵思想的影响下,我们考虑将测量矩阵分成两块,一部分是单位矩阵,另一部分是高斯随机矩阵,即A=[Im×m,C],其中C是(N-m)×N维的高斯随机矩阵. 图1 高斯随机矩阵和优化后的矩阵进行比较 通过图2的上半部分可以看到测量矩阵的列向量相关系数已经较小了,但是还有一部分在0.1的右侧,此时恢复误差为6.721 8×10-15,运行时间为0.006 6,显然恢复效果还算理想;图2的下半部分是对高斯矩阵和单位矩阵形成的测量矩阵进行优化得到的图像,此时恢复误差为1.575 7×10-14,运行时间为0.002 8,测量矩阵的相关性相较于上半部分没有太大变化,这也表明我们的思路是正确的,直接构造的测量矩阵和优化后的测量矩阵在信号恢复中起到的作用几乎一样. 图2 高斯矩阵和单位矩阵形成的测量矩阵和优化后的矩阵进行比较 图3中选择部分哈达玛矩阵作为测量矩阵,此时图像跟之前的高斯随机矩阵的图像相比,列向量相关系数有了明显的下降,而且可以直接对部分哈达玛矩阵进行优化.图3上半部分的恢复误差为1.752 6×10-13,运行时间为0.023 6,下半部分的恢复误差为1.007 5×10-13,运行时间为0.002 8,因此二者的恢复效果没有太大区别,相关性也没有明显变化.通过对图1和图3的比较可知,选择部分哈达玛矩阵作为测量矩阵,其恢复效果明显(就相关性而言)优于高斯随机矩阵,因此接下来将部分哈达玛矩阵用于分块矩阵中,即A=[Im×m,C],其中C是(N-m)×N维的部分哈达玛矩阵. 图3 部分哈达玛矩阵和优化后的矩阵进行比较 通过图4可以看到此时测量矩阵的相关性小于0.1,而且上半部分的恢复误差为1.095 4×10-14,运行时间为0.004 2,下半部分的恢复误差为1.335 8×10-13,运行时间为0.004 4,显然恢复误差可以忽略不计.对于测量矩阵性能的评估,相关性一直是重点关注的指标,在图4中列向量相关系数没有明显的变化,这也说明我们所构造矩阵的合理性和高效性,简而言之,可以将所构造的矩阵直接用于恢复算法中,不再需要进行优化. 图4 部分哈达玛和单位矩阵形成的测量矩阵和优化后的矩阵进行比较 值得指出的是所有信号的恢复所采用的是OMP算法,因此本文单独证明了其算法的收敛性.由于相关性函数不仅与稀疏度s相关,而且与相关性μ相关,因此我们一直在尝试减小相关性μ,在图4中相关性μ明显小于0.1.因此当稀疏度s取得较小值时,此时只要让相关性μ小于0.1,那么一定有μ1(s)+μ1(s-1)<1. 本文基于相干性函数对OMP算法进行了修正,而且通过实验也说明了修正算法的合理性.通过和框架理论的对比得到了这样的结论:当所构造的测量矩阵的行数和列数相差不大时,不需要对测量矩阵进行优化,可以认为此时的矩阵就是最优的.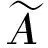
2 主要定理

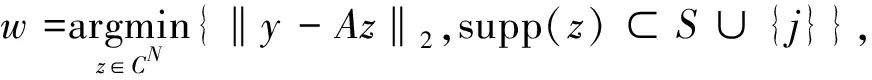
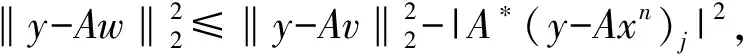
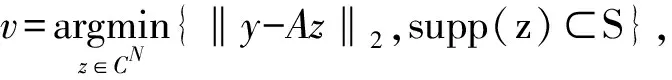
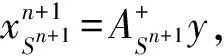
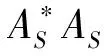
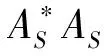
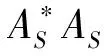
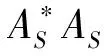


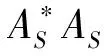
3 数值实验
4 结论
