基于多级箱与深度森林的雷达信号分选算法
2022-07-02张春杰刘俞辰司伟建
张春杰,刘俞辰,司伟建
(1. 哈尔滨工程大学信息与通信工程学院,黑龙江哈尔滨 150001;2. 哈尔滨工程大学先进船舶通信与信息技术工业和信息化部重点实验室,黑龙江哈尔滨 150001)
1 引言
现代雷达电磁环境愈发复杂[1],干扰手段层出不穷[2],电磁频谱分析技术面临严峻的挑战[3]. 雷达信号分选是电子侦察系统中的关键技术,首先利用聚类[4,5]等技术,通过脉内多参数信息将脉冲流稀释成不同电磁空间,再利用到达时间(Time Of Arrival,TOA)分选并提取电磁空间内的信号[6,7]. 然而在复杂电磁环境中,经过稀释后的电磁空间依旧难以被分选:一方面,部分雷达信号脉内信息相似度高,多参数稀释效果不明显;另一方面,雷达信号脉冲重复周期(Pulse Repetition In⁃terval,PRI)调制类型复杂,传统的信号分选算法无法分选大范围抖动、滑变等特殊类型雷达信号. 如何在稀释后的电磁空间中,通过PRI参数将特殊类型雷达信号脉冲分离提取是电磁频谱分析技术的重要一环[8].
传统的单参数PRI 分选算法通过在设定范围内对TOA作差[9~12],或进行PRI变换[13,14],得到PRI峰值进行信号分选,对固定、参差、正常范围抖动雷达信号有着较好的分选效果. 然而,当分选大范围抖动、滑变雷达信号时,其特殊的PRI 统计规律导致其难以被正确分选,中心PRI 值无法得到准确估计,进而难以依据PRI设置容差进行脉冲提取,漏警率高[15]. 不同于固定及参差雷达信号,抖动、滑变雷达信号的PRI 变化范围对于其脉冲提取至关重要[16],尤其面对大范围PRI 变化时,错误的脉冲提取会对后续的辐射源识别、无源定位造成严重影响[17].
针对复杂电磁环境下面对大范围抖动、滑变等特殊类型雷达信号分选时存在的诸多问题,本文将人工智能与传统频谱分析方法深度融合[18,19],提出了一种基于PRI 多级箱与深度森林的雷达信号单参数分选算法. 该方法可在复杂电磁环境下,对大范围抖动、单线性滑变、双线性滑变、锯齿波滑变以及正弦滑变等特殊类型雷达信号进行有效分选,具有较好的PRI范围预测效果与较高的PRI估计精度.
2 复杂电磁环境信号分选挑战
当今的电磁环境相较20世纪,脉冲密度更高,信号调制类型更复杂,给当前的电磁频谱分析技术发展带来了巨大的挑战.
2.1 脉冲丢失
脉冲丢失现象在复杂电磁环境下最常出现,当电磁空间存在少量脉冲丢失时,谐波分量较少,几乎不会对雷达信号分选结果造成影响. 而在密集的脉冲流中,雷达信号脉冲重叠概率增大,脉冲上升沿被覆盖,导致脉冲丢失,低截获概率雷达的出现则进一步加重了脉冲丢失现象,使其难以积累相应的PRI 峰值超过门限,导致雷达信号无法被成功分选.
2.2 新颖的PRI调制类型
滑变雷达信号通过在一定范围内按某种特定规律改变雷达PRI的大小,以达到避免敌方电子对抗设备侦察、干扰敌军、反盲速等目的. 其PRI 变化规律最为复杂,具体为:在一个滑变周期内,以单个或多个滑变间隔的某种排列组合变化PRI 的大小. 常见的滑变类型有单线性、双线性、锯齿波以及正弦滑变. 图1 为滑变雷达4种子类型的PRI变化趋势.
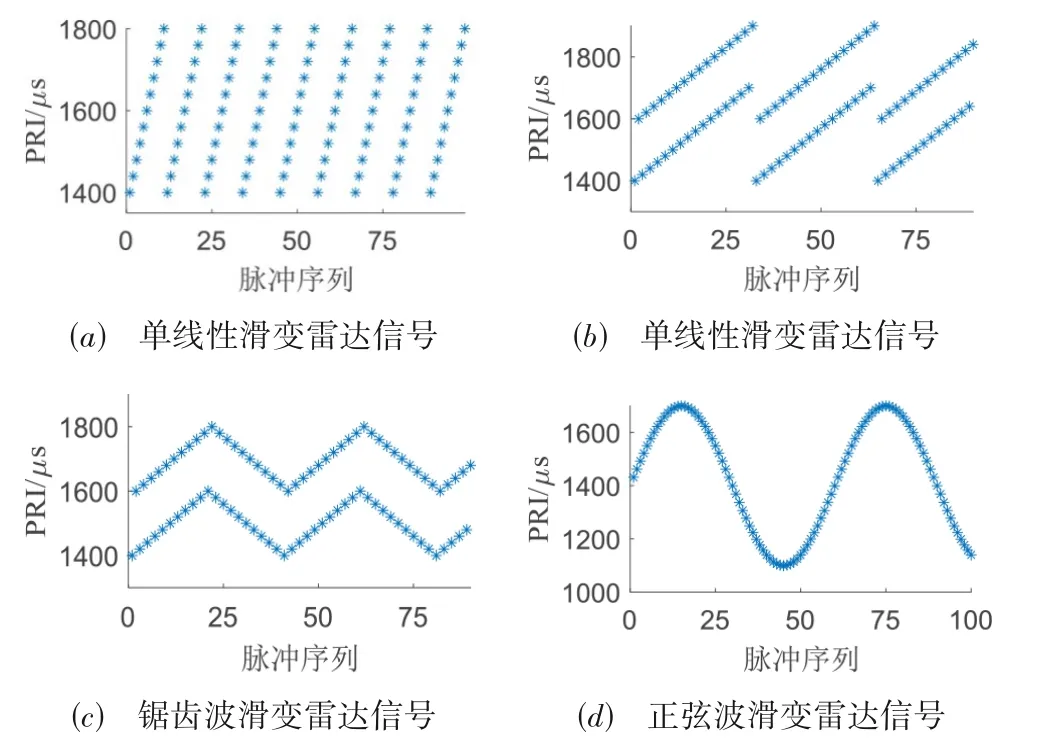
图1 滑变雷达信号子类型
2.3 大范围滑变
随着雷达技术的发展及雷达干扰能力的增强[20],抖动、滑变雷达信号PRI变化范围已不满足于仅占中心PRI 值的30%,进一步向50%延伸. PRI 大范围变化的雷达信号因无法积累足够的PRI 峰值而难以被成功分选,PRI变化范围的增大也使子谐波问题加重,导致PRI峰值偏离PRI 中心,PRI 中心值估计不准,难以进行脉冲提取,从而无法降低电磁环境复杂度.
3 复杂电磁环境信号分选算法
3.1 雷达信号分选架构
在复杂电磁环境下,稀释后的电磁空间依旧混乱,固定、参差、抖动以及滑变等雷达信号相互交错. 文献[7]提出了一种针对复杂电磁环境下固定、参差以及正常抖动雷达信号的分选方法,但未考虑到PRI大范围抖动、滑变等特殊雷达信号类型,其相关脉冲仍遗留在电磁环境中,无法被分选. 因此,本文提出了一种基于多级箱与深度森林的雷达信号分选算法,其基本架构如图2所示.
由图2可知,电磁空间中遗留的特殊类型雷达信号脉冲通过多级箱PRI 变换法,可以检测到超过门限的PRI 峰值;以PRI 峰值为中心,再次进行多级箱PRI 变换,分别记录左右的多级箱中脉冲对个数与PRI变换结果,作为预测PRI 变化范围左右边界的特征. 一般情况下,PRI边界特征受脉冲丢失、子谐波问题影响较大,使用深度森林直接对其预测,偏差较大,无法达到实际应用要求. 因此,本文在提取特征后,分别进行一阶差分、二阶差分处理,并通过平滑滤波器增强其特征,提升深度森林预测效果. 通过预测得到的左右PRI 边界校正PRI中心估计值,并获得PRI变化范围,提取相应脉冲.若电磁环境仍有雷达信号残留,则重复此过程.

图2 复杂电磁环境信号分选架构
3.2 多级箱PRI变换法
为解决修正PRI变换法无法分选大范围抖动、滑变雷达信号的问题[13],多级箱PRI变换法在修正PRI变换法基础上提出多级PRI箱结构,通过多级PRI箱结果累加,增大特殊雷达信号的分选正确率.
将电磁空间中的脉冲序列看作冲激函数δ(∙),即

其中,N为脉冲个数;tn(n=0,1,2,…,N-1)为脉冲序列到达时间. 考虑将g(t)的积分变换为

其中,τ代表脉冲间到达时间差;exp(j2πt τ)为相位因子.PRI 变换法通过引入相位因子,有效抑制子谐波影响,将式(1)代入式(2)得到PRI变换法的离散形式,即

将电磁空间内的抖动、滑变等雷达信号脉冲序列建模表示为

其中,T为抖动、滑变雷达信号PRI 中心值;εk为相邻两脉冲较PRI中心值的偏差百分比,εk平均值为0. 由此推导相邻两脉冲相位为

两个相位θ1和θ2,若满足θ1=θ2mod 2π 或exp(jθ1) =exp(jθ2),则可认为二者相等,于是有
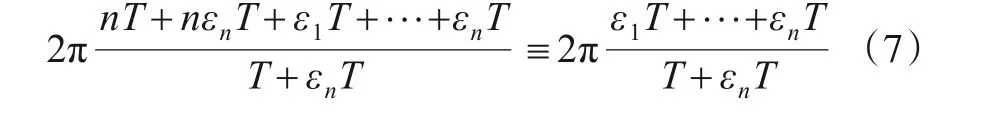
将式(7)变形代入式(6),当n较大时,有

假设抖动、滑变雷达信号脉冲符合均匀分布,则
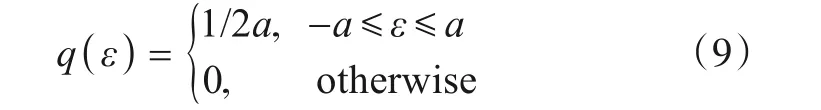
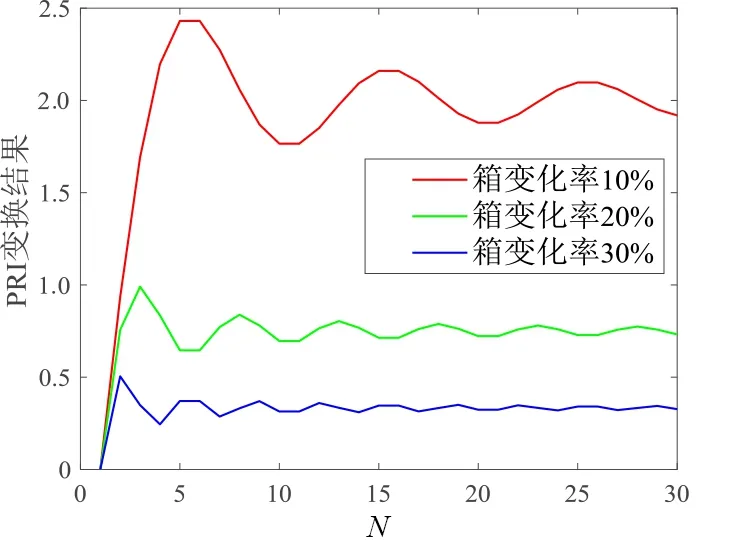
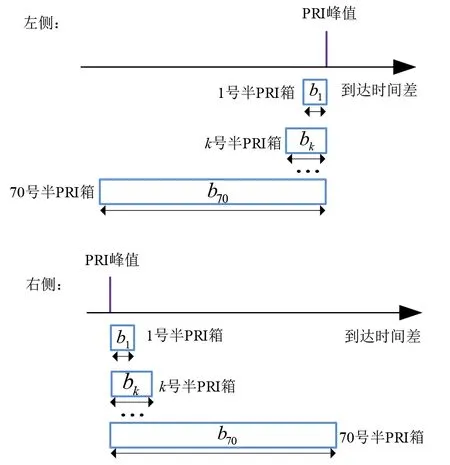
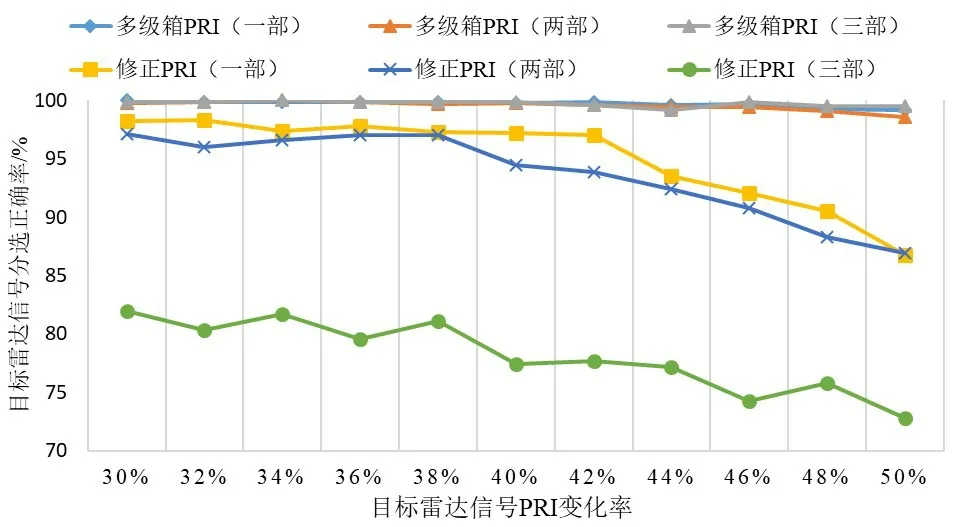
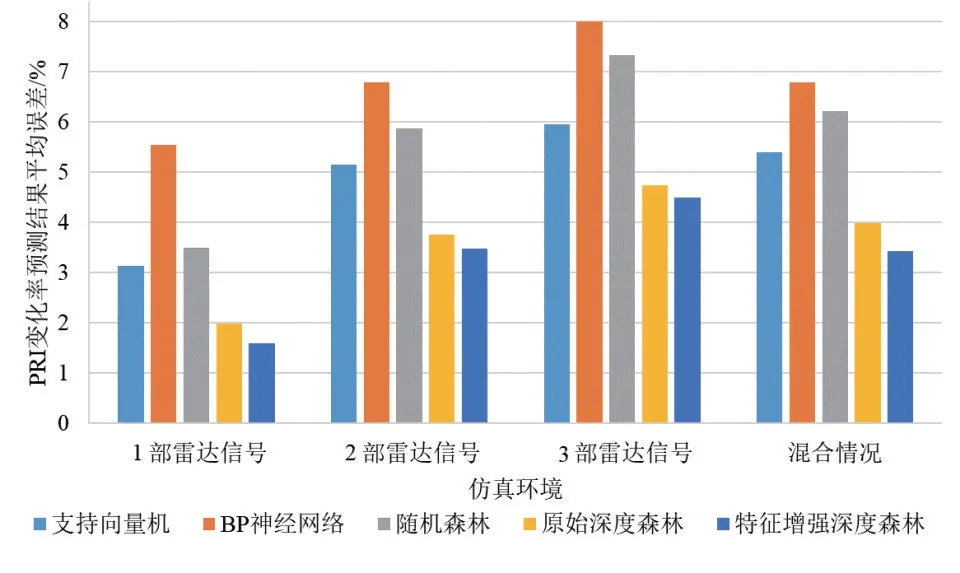
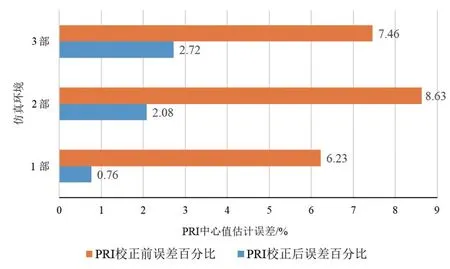
其中,a为PRI变化率(0 不同箱变化率下的最佳PRI变换曲线如图3所示. 由图3 可知,对大范围抖动、滑变雷达信号进行PRI 变换时,大变化率交叠箱对应PRI 变换曲线可积累值小,而小变化率交叠箱可积累值大,但进入箱中脉冲对个数少,修正PRI 变换法通过可变化时间起点,使N维持在较小值,从而得到高积累值. 图3 不同箱变化率下的最佳PRI变换曲线 实际电磁环境中,交叠箱变化率难以选择,若交叠箱变化率较雷达信号PRI变化率过小,箱内脉冲数积累不足,峰值无法超过门限;反之,交叠箱变化率大于雷达信号PRI 变化率,多个交叠箱PRI 变换结果相同,则不会出现PRI峰值. 多级箱PRI 变换法针对大范围抖动、滑变雷达信号,设置多个变化率交叠箱,通过多个交叠箱结果累加得到PRI 峰值,既保证了峰值超过门限,又避免了交叠箱PRI 变换结果相同. 为保证覆盖30%~50%范围变化的雷达信号,应至少设置三级箱,设每级箱个数K为300,则一、二、三级箱分别为300 个变化率为50%,40%,30%的交叠箱,每级箱间隔相等,从而保证多级箱PRI 变换法在30%~50%间具有均衡的PRI 分选效果.由于通过三级PRI箱PRI变换结果累加,已可以实现特殊雷达信号的分选,因此加大级箱数,不仅会造成复杂度的增加,PRI分选提升效果也不明显. 预测PRI 边界,依据PRI 变化范围校正PRI 中心值,对于分选大范围抖动、滑变等特殊类型雷达信号尤为重要. 在电磁空间中,面对未知变化范围的雷达信号,即使可将其分选为一部雷达信号,但还是无法将其进行脉冲搜索提取. 设置搜索范围过小,会导致本雷达信号脉冲搜索不全;而范围过大,则极易将其余雷达信号脉冲搜索为本部雷达信号并进行提取,从而破坏了其他信号的完整性. 除此之外,特殊类型雷达信号PRI变化范围广,会产生明显的子谐波问题,严重影响中心PRI值估计精度. 本文通过深度森林实现对PRI边界的预测,获得PRI 变化范围,从而对目标雷达信号进行更完整的脉冲序列提取,并通过PRI 校正,实现雷达信号中心PRI值高精度估计. 基于深度森林的PRI边界预测流程图如图4所示. 图4 基于深度森林的PRI边界预测流程图 3.3.1 PRI边界特征提取 在复杂电磁环境中,PRI 多级箱变换法得到的PRI峰值易受子谐波干扰,从而偏离原本PRI 中心值. 因此,要将PRI 边界预测划分为PRI 左边界与PRI 右边界预测两部分. 由于在PRI变化范围边界附近,雷达信号脉冲分布变化明显,因此,以PRI峰值位置为中心分别向左、向右建立1%~70%变化率的半PRI 箱,以PRI 峰值位置为中心重新进行PRI 变换. 半PRI 箱示意图如图5 所示. 其中PRIc为PRI峰值,则k号箱的宽度bk为 图5 半PRI箱示意图 提取各半PRI 箱中的脉冲对个数结果与PRI 变换结果作为PRI 边界特征,在PRI 边界外,雷达信号脉冲消失,因此脉冲个数结果与PRI变换结果曲线在PRI边界位置会产生斜率变化. 然而,在实际电磁环境中,脉冲对个数结果与PRI变换结果曲线经常出现不规律波动,斜率变化不明显.本文通过对脉冲对个数结果与PRI 变换结果进行一阶与二阶差分,减轻数据间的不规律波动,增强特征. 3.3.2 平滑滤波增强特征 在复杂电磁环境中,子谐波问题加大了PRI边界预测的难度,而左侧PRI 边界特征受子谐波影响小,因此左侧PRI 边界预测效果明显优于右侧PRI 边界预测效果. 平滑滤波是一种低频增强的空间滤波技术,可以较好地增强低频PRI 边界的脉冲对个数变化以及PRI 变换结果特征,抑制高频子谐波影响. 但同时,也会对特征产生一定的模糊效果. 本文提出的平滑滤波增强边界特征结构如图6 所示. 对平滑后的各箱中脉冲对个数结果与PRI 变换结果进行一阶与二阶差分,再利用平滑滤波器分别对其进行平滑,增强PRI 边界特征. 平滑前后脉冲对个数结果与PRI 变换结果二阶差分结果如图7 所示,经过平滑后的二阶差分结果在实际PRI 边界21.08 附近更加明显. 图6 平滑滤波增强边界特征结构 图7 平滑滤波增强前后效果对比 3.3.3 深度森林预测PRI边界 深度随机森林由文献[19]提出,是一种基于随机森林的有监督集成学习算法,其受到深度学习理论与时滞神经网络的启发,通过对决策树构成的森林深度与广度两方面的集成与串联,从而实现分类及预测效果的提升. 深度森林由多粒度扫描与级联森林两部分组成.以三分类问题为例,深度森林结构如图8所示[21]. 图8 深度森林结构图 多粒度扫描通过多尺度滑动窗口对序列数据进行采样,可以得到包含更多特征子样本的局部序列,丰富特征达到增强的效果,并通过极端森林与随机森林对扫描结果进行处理,最终将处理结果拼接,作为级联森林的输入用于训练级联森林. 针对序列间存在顺序关系的PRI边界特征,多粒度扫描可有效提高级联森林预测效果. 级联森林的每一层由极端森林与随机森林组成,除第一层输入为多粒度扫描结果外,其余每层的输入都为前一层输出特征与原始特征的组合. 通过逐层处理数据,预测效果逐渐增强,当预测效果下降时,停止训练. 本文设置的级联森林每层包括两个极端森林与两个随机森林,极端森林与随机森林中均包含500棵决策树. 极端森林也称作完全随机森林,不同于随机森林随机采样作为训练集,极端森林使用所有样本,在全部样本中随机选择特征作为训练集,泛化能力优于随机森林. 级联森林利用多粒度扫描拼接融合后的特征结合stacking 策略进行深度学习. 不需设置超参数,而且具有更加稳定的学习性能. 本文通过仿真复杂电磁环境生成数据集,电磁环境包括1 部、2 部、3 部雷达信号,雷达信号类型包括大范围抖动雷达信号、单线性滑变雷达信号、双线性滑变雷达信号、锯齿波滑变雷达信号与正弦滑变雷达信号,PRI 变化范围均为30%~50%,电磁环境丢失率为0%~25%,共生成左右PRI 边界特征序列各25 000 组,每组包含1%~70%半PRI 箱中脉冲对个数结果与PRI 变换结果的一阶差分与二阶差分特征. 其中24 000 组数据用于训练,1 000 组数据用于测试. 当连续两次训练损失值未减小时,训练停止,左侧PRI 边界预测深度森林包含8层,右侧PRI边界预测深度森林包含5层. 依据多级箱PRI峰值与左右变化边界预测结果,推导出雷达信号PRI中心值为 PRI=PRIc(1+(range2-range1)/200)(12) 其中,PRI为中心值;PRIc为峰值;range1,range2为左右PRI边界,range1,range2 ∊(0,70). 凭借PRI中心值与PRI变化范围在电磁空间内展开脉冲序列搜索,弥补了文献[16]需提前预设最大抖动率的缺陷,达到了更好的脉冲序列搜索效果,从而实现了在复杂电磁环境下对特殊类型雷达信号的正确分选、PRI 中心值的准确估计、PRI变化范围预测,以及脉冲序列的搜索提取. 仿真3种电磁环境,分别包含1部、2部、3部雷达信号,信号类型包含大范围抖动、单线性滑变、双线性滑变、锯齿波滑变、正弦滑变,除PRI 外其余参数完全相同,丢失率在0~25%中随机选择. 目标雷达信号PRI变化率选择范围为30%~50%,共11 种目标雷达信号PRI变化率. 分别选择PRI多级箱变换法与修正PRI变换法对目标雷达信号进行分选,对33 种情况各进行蒙特卡洛实验1 000次,共33 000次,其中PRI多级箱变换法交叠箱变化率为30%,40%,50%,修正PRI 变换法交叠箱变化率取变化范围中心40%. 目标雷达信号分选正确率如图9所示. 图9 目标雷达信号分选正确率 由图9 可知,多级箱PRI 变换法与修正PRI 变换法在较简单雷达环境中针对目标雷达信号有较高的分选正确率,而当电磁环境中雷达信号个数增多、子谐波问题加重、丢失率影响开始显现时,修正PRI 变换法分选正确率明显下降,而多级箱PRI变换法通过融合各级箱PRI 谱图,依旧能使PRI 峰值超过门限,具有较高的分选正确率. 仿真4种电磁环境,分别包含1部、2部、3部雷达信号以及各情况随机混合,雷达信号类型包含大范围抖动、单线性滑变、双线性滑变、锯齿波滑变、正弦滑变,除PRI 外其余参数完全相同,丢失率在0~25%中随机设定. 雷达信号PRI 变化率在30%~50%中随机选取,分别选择支持向量机、BP 神经网络、随机森林、原始深度森林、平滑特征增强深度森林进行左右PRI 边界预测,每种环境分别包含1 000 组左右PRI 边界特征. 左右PRI边界预测结果平均绝对误差如图10、图11所示. 图10 左侧PRI边界预测结果平均绝对误差 图11 右侧PRI边界预测结果平均绝对误差 由图10 可知,在左侧PRI 边界预测中,混合情况下平滑特征增强深度森林预测PRI 变化率结果平均绝对误差为0.615%,原始深度森林为0.62%,而支持向量机、BP 神经网络和随机森林分别为1.309%,1.237%和0.748%. 由于左侧受子谐波干扰少,特征较明显,因此平滑特征增强效果较弱. 而由图11可知,在右侧PRI边界预测中,混合情况下平滑特征增强深度森林预测结果平均绝对误差为3.423%,原始深度森林为3.994%,而支持向量机、BP 神经网络和随机森林分别为5.389%,6.789%和6.217%. 平滑特征增强森林较原始深度森林提升了14%的右侧PRI边界预测效果. PRI 边界预测效果优劣最终体现在PRI 中心值校正误差大小上. 因此仿真3种电磁环境对PRI校正结果前后误差展开分析,电磁环境分别包含1 部、2 部、3 部雷达信号,包含5 种信号类型,除PRI 外其余参数完全相同,丢失率在0~25%中随机选择. 每种电磁环境进行1 000次蒙特卡洛实验,PRI校正前后目标雷达信号PRI中心值估计误差对比图如图12所示. 由图12 可知,校正后的PRI 中心值误差大幅小于未经校正的PRI谱图峰值.1部雷达信号条件下,PRI估计误差降低了87.8%;2 部雷达信号条件下,PRI 估计误差降低75.9%;3 部雷达信号条件下,PRI 估计误差降低63.5%. 平均PRI 估计误差降低75%,当雷达电磁环境趋于复杂时,PRI 中心值校正误差随PRI 边界预测误差增大而增加,而校正前的PRI中心值受电磁环境复杂度影响不大. 通过准确的PRI 中心值与PRI 变化范围,可以在电磁空间脉冲序列中更好地搜索目标雷达信号脉冲. 图12 PRI校正前后PRI中心值估计误差对比图 本文针对复杂电磁环境下大范围抖动、滑变等特殊类型雷达信号分选时存在的诸多问题,提出了一种基于PRI 多级箱与深度森林的雷达信号单参数分选算法. 该方法将雷达频谱分析算法与人工智能深度融合,提升了针对特殊类型雷达信号的分选正确率,自主预测PRI变化范围,通过平滑滤波增强特征来进一步降低预测误差,校正PRI 中心值提高PRI 估计精度,改善了子谐波问题对其的影响,脉冲搜索提取效果更佳. 仿真实验表明:所提算法可在复杂电磁环境下对大范围抖动、单线性滑变、双线性滑变、锯齿波滑变、正弦滑变等特殊类型雷达信号进行有效分选,在原始深度森林PRI范围预测效果的基础上提升了14%,PRI估计误差降低了75%,具有较好的PRI 范围预测效果与较高的PRI 估计精度,可以解决复杂电磁环境下针对特殊类型雷达信号的分选问题.
3.3 基于深度森林的PRI边界预测

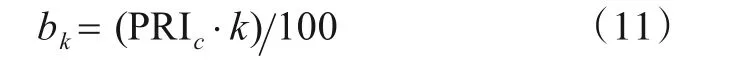


3.4 PRI校正与脉冲提取
4 仿真实验与性能分析
4.1 多级箱PRI变换法分选效果分析
4.2 PRI边界预测效果分析

4.3 PRI校正结果误差分析
5 结论
