基于多重分形谱智能分析的卫星信号调制识别研究
2022-07-02杨伟超侯舒维徐常志张建华
杨伟超,杜 宇,文 伟,侯舒维,徐常志,张建华
(中国空间技术研究院西安分院,陕西西安 710100)
1 引言
信号调制方式识别是无线电领域的热点研究问题,在卫星通信抗干扰、电磁频谱战及无线电监管等军民领域有着广泛的应用. 经过多年的发展,信号调制方式识别形成了基于决策理论的最大似然假设检验和基于特征提取的模式识别两类方法[1~4],人工智能的到来,为其带来了新的思路. 近些年来,涌现出了一大批基于深度学习的调制识别方法[5~11],该类方法充分利用了深度网络结构的自适应能力和迁移扩展能力. 文献[6,7]提取信号的星座图,并结合经典卷积神经网络(CNN)实现了信号的调制识别. 文献[8]针对监督学习中数据分布不完备问题,提出了一种对抗域适应迁移算法,直接利用了信号的波形特征. 文献[9]提取调制信号的相位和幅度信息,根据特征将双向长短时记忆层串联,构建了双向长短时记忆识别模型. 文献[10]利用了信号的实部和虚部的聚类特征,其亮点在于构建了AMC2N(双通道胶囊网络). 文献[6~10]利用了常规的信号时频域特征,并采用不同的深度学习网络提取特征实现信号识别,此类方法的优势在于原理简单、易于理解、计算量小,但信号的时频域特征对噪声比较敏感,故此类方法抗噪性能较差. 文献[11]在提取信号核空间时频特征的基础上,采用了稀疏域去噪来降低噪声影响,并采用核空间降维等方法构建了栈式稀疏降噪自编码识别网络,相对于文献[6~10]方法,该方法具有较好的抗噪性能,但计算过程相对烦琐、不易于工程应用. 上述方法均利用了深度学习的智能化特征提取和分类优势,但其特征域相对单一,此类特征只能从某一维度或层次描述信号的个体特征,如时频特征、星座图、幅度相位等,不能深层次多维度全面刻画信号,包含信息量有限,故深度学习的多层次细节化特征分析能力也不能充分发挥作用. 多重分形是分形理论中的一个重要概念,其可从多维度深层次描述通信信号的复杂度特征. 文献[12,13]提出了基于多重分形谱的通信信号调制识别方法,利用了多重分形谱的奇异指数的最大值与最小值、极大值对应的奇异指数、谱宽度、谱跨度等特征,但此类特征依然不能完整描述多重分形谱的整体分布特性,故不能全面体现多重分形谱对信号的多层多尺度呈现能力,且方法智能化程度较低.
鉴于上述原因,本文提出了基于多重分形谱与残差神经网络相结合的智能调制识别算法. 算法在分析常用卫星通信相位调制信号多重分形谱特征的基础上,根据多重分形谱计算中盒子尺度的不同构建了待识别信号多重分形谱矩阵,并将其作为网络的输入,利用了多重分形谱可全面完整刻画通信信号内部特征的优势,同时利用了残差神经网络优异的多层次细节提取分析能力,实现了卫星通信中应用较多且较难区分的几种相位调制信号的识别.
2 多重分形谱
众所周知,通信信号是一种时间序列,不同调制方式的信号,其时域特征存在差异,调制识别是从全局到细节的深化过程,从本质上而言,分形理论与之类似.分形是非线性领域的一个重要方向,其研究对象具有非线性、几何特征不规则、自相似、结构精细等多种特征,是一类刻画物质不规则性和复杂度的方法论[14].
多重分形谱是分形中的重要理论之一,文献[14]中提到“多重分形是定义在分形结构上的由多个标量指数的奇异测度(不存在测度密度的测度)所构成的集合. 它描述了分形测度在支集上的分布情况,即用一个谱函数来刻画分形对象不同层次上的特征. 这是从分形的局部出发,根据自相似特性,研究其最终整体特征的理论基础”,可见,多重分形谱是一种根据自相似性描述对象多层次特征的集合. 此外,文献[14]同时指出“多重分形谱除了能精确的表征通信信号波形的几何特征信息,还能对信号的不规则性、复杂度及全局正则性进行定量的刻画,可以更有效地描述不同信号调制方式之间的差别”,亦即多重分形谱是一种有效的调制识别特征.
多重分形谱可采用基于Rèny广义维数或测度理论进行定义[14~16],本文采用基于测度理论的方法.
2.1 多重分形谱定义
假设X是d维度量或欧氏空间xd中的子集,即某系统的恒定集或测度子集. 对X进行某种递归或迭代划分,并采用恒定概率的测度μ对其进行描述. 参数η与划分相关,X经过n步划分后记为Xn(η).

如果(X,μ)被划分成若干个单元,单元尺度大小为δ,且该尺度与单元测度μα遵循以下关系:

则称η为Lipschitz-hölder 指数,亦称奇异性指数,奇异性指数η和单元尺度δ共同表征单元测度.
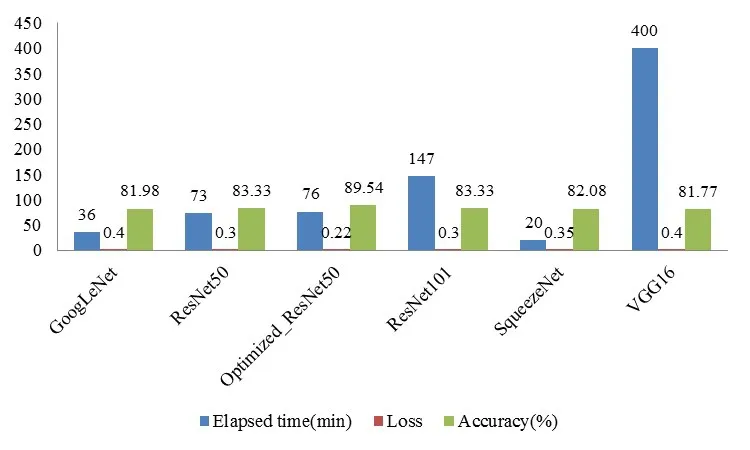
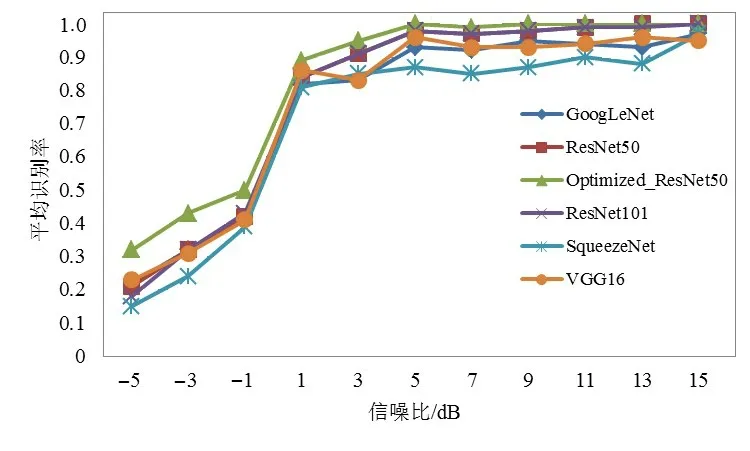
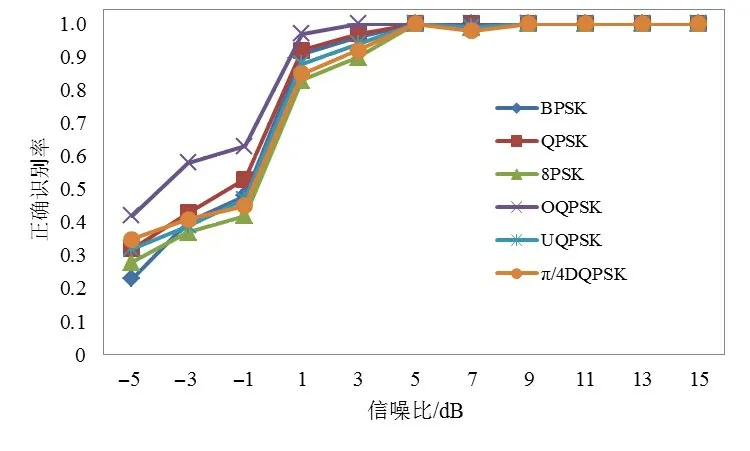
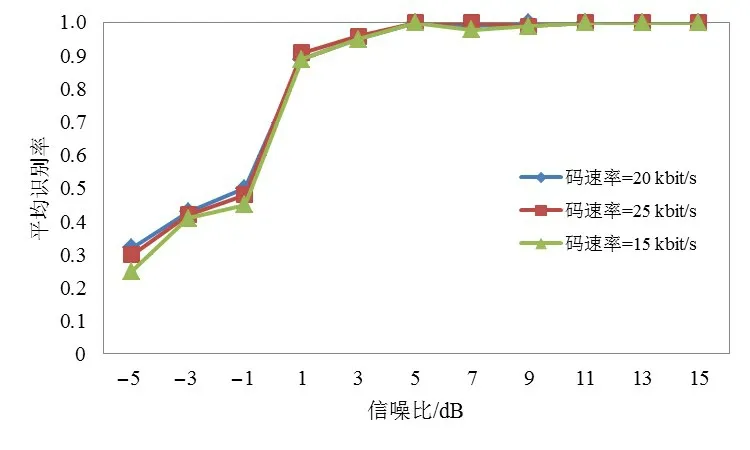
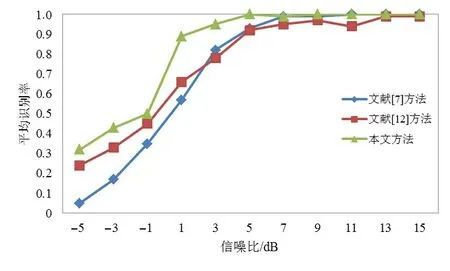
假设分形子集Xη的概率测度为μη,其任意可列δ覆盖{Ui}(i∊N),即0 其中,inf 表示下界,上式即为所有可列δ覆盖直径取和的最小值. 则(X,μ)的r维Hausdorff 测度可表示为其中,μη为分形子集Xη的概率测度,则Hausdorff测度可理解为其任意可列δ覆盖中当单元尺度δ无限趋近于0时,所有可列覆盖直径取和的最小值. 假如临界指数f(η)存在,当r>f(η)时,℘r(Xη,μη) =0;当r 奇异谱f(η)是随奇异性指数η变化的单峰曲线,如图1 所示,其在η轴占据区域的范围表征了多重分形特征不同程度上的强弱,即较大的奇异指数范围Δη对应较强的多重特征,且Δη越小越趋近于单重分形. 奇异谱和奇异性指数是刻画多重分形细节特征的一套基本理论. 图1 BPSK信号多重分形谱 本节采用直接计算法[17]来近似估计多重分形谱,相关步骤如下所述. (1)计算概率测度Pi(δ). 折线长度是计算概率测度的有效工具,对于信号序列,其折线长度定义如下: 其中,xj表示信号序列中的第j个点. 从上式可以看出,信号序列折线全长L=LL(N). 当盒子尺寸为δ时,第i个盒子内全部信号的折线总长设为LLi(δ),概率测度可计算如下: (2)对于权重因子q(-∞ 其中,δ为盒子尺寸;q值描述了不同概率测度在配分函数中所占比重或贡献的大小. 此外,权重因子q还可对特定区域内的奇异特性进行深层次微观表征,当q>1时,χq(δ)可对Pi(δ)的强奇异性部分放大描述;当q<1时,χq(δ)着重描述Pi(δ)的弱奇异性部分;当q=1时,维持不变. (3)计算质量指数τ(q). 对于上式的双对数计算,可采用最小二乘直线拟合的方法估算. (4)分别估算奇异性指数η和奇异谱f(η),得到多重分形谱. 在卫星通信中,相移键控是应用最多的一种调制方式,其中又以BPSK,QPSK,8PSK,OQPSK,UQPSK 和π/4DQPSK 几种信号最为常见,本文从航天电子侦察对抗实际需求出发,主要研究上述几种信号的调制识别,其多重分形谱如图2所示. 图2 待识别信号多重分形谱 从图2可以看出,待识别的几种信号多重分形谱图有诸多细节差异,如谱跨度、谱曲率、奇异性指数最大最小值等. 事实上,从多重分形谱的计算过程可以看出,概率测度中盒子尺寸δ和配分函数中权重因子q亦是影响多重分形谱的重要因素,此处为了更全面的表征多重分形谱及最大化图2中待识别信号类间差异,构建了多重分形谱矩阵. 构建思路如下: (1)如前所述,权重因子q还可对特定区域内的奇异特性进行深层次微观表征,为了全面的描述强奇异性区域和弱奇异性区域,同时综合考虑计算量问题,取权重因子q区间为[-10:0.2:10],其代表列因子,亦即共101列. (2)相同信号,盒子尺寸δ不同时,其多重分形谱分布有较大不同,故对上述6种待识别信号多重分形谱盒子尺寸δ统一取5,10,20,30,40共5类,其为行因子,亦即共5行. (3)由前述两条原则可知,多重分形谱矩阵规模为5×101,6类待识别信号多重分形谱矩阵如图3所示. 由图2、图3及上述分析可以看出,调制识别已由一维信号分类演化为二维图像识别问题,且6类信号多重分形谱矩阵二维图像存在诸多差异,是一种有效的识别特征. 但多重分形谱矩阵二维图像中谱细节纷繁复杂,传统的特征提取方法很难覆盖全面,深度学习中的残差网络为我们提供了一个很好的思路. 图3 信号多重分形谱矩阵 深度残差网络(ResNet)是2015年提出的一种网络结构,其借鉴引入了残差的思想,使传统深度卷积网络中存在的梯度消失和精度下降(训练集)问题得到了有效解决. 残差网络结构中假设x为输入数据,F(x)表示残差映射,则其特征输出H(x)为 其中,若F(x) >0,表示该卷积层学习到新的特征信息,从而保证反向传播时的梯度传递. 且从残差计算式可知,残差表征输入和输出的差异,一般较输出要小,或者说,残差学习相较于直接学习内容要少,难度相对较小. 因此,该型网络更易优化,且增加网络结构的深度有利于提取更多的特征,进而提升模型效能. 关于深度残差网络的理论在互联网及以往文献中有诸多报道,此处不再赘述. 经过几年发展,ResNet[18,19]衍生出了ResNet50,ResNet101 等多种不同卷积层深度的网络结构.ResNet50 网络结构主要由多个残差模块构成,其结构如图4左侧实线部分所示. ResNet50 网络结构包括1 个全连接层和49 个卷积层,网络模型运行分6 个阶段进行. 其中,第一阶段包含卷积、批量正则化、激活函数和最大池化操作;第二至第五阶段包含卷积残差模块和恒等残差模块;第六阶段则包含全局平均池化层操作及全连接层的Softmax分类器. 上述网络结构在逐层演化的过程中,会对图像进行尺度缩放,为了让不同颗粒度级别的信息参与最终分类,从而提高识别正确率,本文对ResNet50 网络结构进行了优化改进,即Optimized_ResNet50,如图4 所示(虚线框部分),即将第三阶段结果也作为第六阶段分类的输入特征. 优化模块包含2 个卷积层和1 个池化层,主要起到尺寸缩放和特征增强的作用. 图4 Optimized_ResNet50网络结构图 为了验证所提方法的有效性,基于MATLAB 软件平台和惠普Z840 工作站进行了仿真评估. 信号参数均为:中频50 kHz,码速率20 kbit/s,采样频率200 kHz. 训练样本为-5 dB,0 dB,5 dB,10 dB,15 dB 每个信噪比下200 张二维矩阵图,6 种信号共6 000 个样本. 以下分别从网络结构、信噪比、信号参数、盒子尺寸数量、以往相关算法性能比较等几方面对所提方法进行了评估分析. 深度神经网络多种多样、结构各异,不同的神经网络架构可能适用于不同的领域,不能一概而论. 本文选取在图像识别中具有显著优势的5类经典网络架构和本文优化后的网络架构,即GoogLeNet[20],ResNet50,Opti⁃mized_ResNet50,ResNet101,VGG16[21]和SqueezeNet[22],针对上述信号的多重分形谱矩阵二维图像识别进行了仿真分析,分别从训练及测试两方面进行了评估. 测试中,取每种信号在[-5:2:15]dB 区间每个信噪比下100组数据,共计6 600 组数据作为测试样本,结果如图5、图6所示. 图5 网络训练情况 图6 不同网络识别结果 由图5可知,在网络训练中,VGG16在网络损失、耗时、训练识别率等方面均为最差,GoogLeNet 和SqueezeNet虽耗时较少,但其网络损失和训练识别率较差,ResNet50,ResNet101 及Optimized_ResNet50 整体性能具有明显的优势,而其中又以Optimized_ResNet50 性能最为突出. 此外,Optimized_ResNet50 与ResNet50 耗时基本相当,说明前述优化改进方法在不大量增加网络复杂度的情况下,明显提升了网络效能. 图6 为测试结果,从图中可以看出,在整个信噪比范围内,测试识别率趋势与训练识别率趋势类似,Opti⁃mized_ResNet50 最优,ResNet50 和ResNet101 次之,GoogLeNet,SqueezeNet,VGG16 较差. 进一步说明了Optimized_ResNet50网络结构的优异性. 为了更清晰具体了解每种信号的识别情况,对每种信号进行了噪声影响仿真分析,测试样本同4.1 节,测试结果如图7所示. 由图7可以看出,整体而言,在测试信噪比范围内,当信噪比不小于1 dB 时,平均识别率大于89%. 当信噪比小于1 dB 时,噪声在多重分形谱中起了主导作用,故该区域识别性能整体较差;从单个信号角度来看,上述6 种信号中,OQPSK 信号识别性能明显优于其他信号,究其原因,OQPSK 信号波形突变最小,其多重分形谱特征最明显,这也与图2 结果相符. 其次,该项测试样本与训练样本信噪比并不完全相同,说明该方法有较好的泛化能力. 图7 不同信噪比下识别结果 在电子侦察中,射频信号经接收机下变频到固定中频,且在后续信号调制识别中,为了避免信号幅度变化的影响,会对接收信号幅度进行最大值归一化处理,那么信号的码速率就成为影响调制识别性能的主要因素,本节分析不同信号码速率对方法的影响. 上述仿真中码速率为20 kbit/s,此处增加了码速率为25 kbit/s 和15 kbit/s时的仿真测试,结果如图8所示. 图8 不同码速率识别结果 由图8 可知,3 种码速率情况下本文方法识别性能相当,说明本文方法对信号参数变换不敏感,具有较好的鲁棒性和适应性. 多重分形特征矩阵是整个算法的核心,直接决定着最终识别效果的优劣. 由第2 节可知,多重分形谱矩阵由盒子尺寸数量和权重因子两类元素构成,权重因子仅改变信号多重分形谱线离散点的疏密程度,并不改变多重分形谱的分布特性,因此,盒子尺寸数量是影响多重分形谱矩阵细节特征的主要因素. 本节仿真分析盒子尺寸数量对方法性能的影响,仿真中,盒子尺寸包含5,10,20,30,40,50 共6 类,不同数量盒子依照从左到右的选取原则. 仿真结果如图9所示. 图9 不同盒子尺寸数量识别结果 从图9可以看出,盒子尺寸数量(特征矩阵行向量)越多,识别性能越好,因为较多的盒子尺寸包含了更丰富的细节信息,可以帮助提高识别率. 此外,随着盒子尺寸数量的增加,识别性能提升逐渐趋缓,说明盒子尺寸达到一定数量后,会产生一定的冗余信息. 综合考虑识别性能和计算量,本文选取5类盒子尺寸构建了特征矩阵. 为了对算法有一个较为全面的评估,下面对本文方法和两类典型代表性方法进行了比较分析. 文献[7]是应用深度学习智能识别的代表性方法,文献[12]是将多重分形谱作为识别特征的代表性方法. 识别性能比较结果如图10所示. 图10 不同方法识别结果 由图10可知,在整个设定的信噪比范围内,本文方法整体识别性能优于另外2种方法,说明本文将深度学习与多重分形谱“强强联合”的方法更具优越性. 本文基于多重分形谱可有效刻画通信信号不同层次特征的特性,构建了特征域矩阵,并对ResNet50 网络架构进行了多尺度优化改进,利用改进后网络对多重分形谱特征矩阵进行多层次智能化提取,有效实现了卫星通信中常用相位调制信号的有效识别,仿真结果证明了该方法的有效性. 此外,从多重分形谱的计算过程可以看出,无复杂计算模块,计算量小,且ResNet50网络模型成熟,已广泛应用,故本文方法易于工程实现.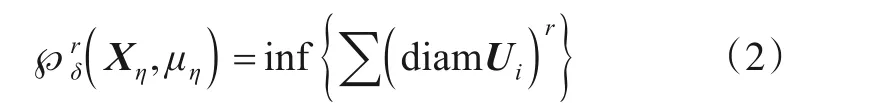
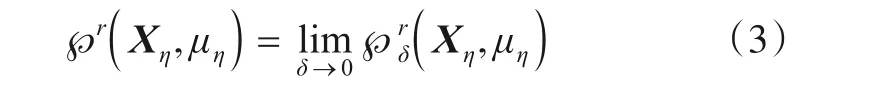



2.2 多重分形谱计算方法



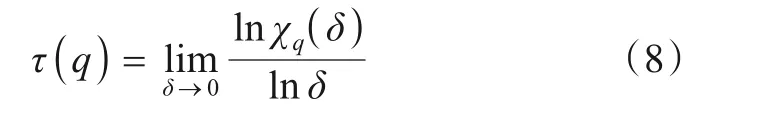
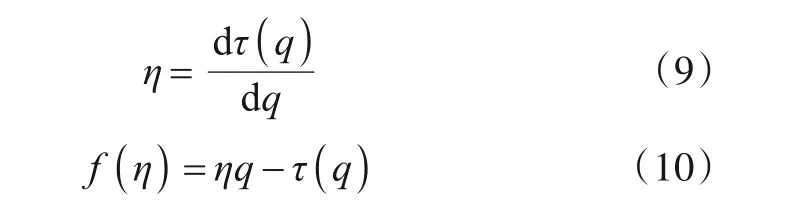
2.3 多重分形谱矩阵构建方法


3 深度残差网络


4 仿真试验与分析
4.1 网络结构对方法性能的影响分析
4.2 噪声对方法性能的影响分析
4.3 信号参数对方法性能的影响分析
4.4 盒子尺寸数量对方法性能的影响分析

4.5 与以往方法识别性能比较
5 结论
